SIMD-based Implementations of Eta Pairing Over Finite Fields
of Small Characteristics
Anup Kr. Bhattacharya
1
, Abhijit Das
1
, Dipanwita Roychowdhury
1
, Bhargav Bellur
2
and Aravind Iyer
2
1
Department of Computer Science and Engineering, Indian Institute of Technology Kharagpur, Kharagpur 721302, India
2
General Motors Technical Centre India, India Science Lab, Bangalore 560066, India
K
eywords:
Supersingular Elliptic Curves, Eta Pairing, Software Implementation, SIMD, SSE Intrinsics.
Abstract:
Eta pairing on supersingular elliptic curves defined over fields of characteristics two and three is a popular
and practical variant of pairing used in many cryptographic protocols. In this paper, we study SIMD-based
implementations of eta pairing over these fields. Our implementations use standard SIMD-based vectorization
techniques which we call horizontal and vertical vectorization. To the best of our knowledge, we are the first
to study vertical vectorization in the context of curves over fields of small characteristics. Our experimentation
using SSE2 intrinsics reveals that vertical vectorization outperforms horizontal vectorization.
1 INTRODUCTION
Pairing over algebraic curves are extensively
used (Boneh and Franklin, 2001; Joux, 2004; Boneh
et al., 2004) in designing cryptographic protocols.
There are two advantages of using pairing in these
protocols. Some new functions are realized using
pairing (Boneh and Franklin, 2001; Joux, 2004).
Many other protocols (Boneh et al., 2004) achieve
small signature sizes at the same security level.
Miller’s algorithm (Miller, 2004) is an efficient
way to compute pairing. Tate and Weil are two main
variants of pairing functions on elliptic curves, with
Tate pairing computation being significantly faster
than Weil pairing for small fields. In the last few
years, many variants of Tate pairing (Barreto et al.,
2007; Hess et al., 2006; Lee et al., 2009) are proposed
to reduce the computation complexity of Tate pair-
ing substantially. Eta pairing (Barreto et al., 2007)
is one such variant defined for supersingular curves.
Some pairing-friendly families (Freeman et al., 2010)
of curves are defined over prime fields and over fields
of characteristics two and three. (Vercauteren, 2010)
proposes the concept of optimal pairing which gives
lower bounds on the number of Miller iterations re-
quired to compute pairing.
There have been many attempts to compute pair-
ing faster. (Barreto et al., 2002) propose many simpli-
fications of Tate-pairing algorithms. Final exponenti-
ation is one such time-consuming step in pairing com-
putation. (Scott et al., 2009) propose elegant meth-
ods to reduce the complexity of final exponentiation.
(Ahmadi et al., 2007) and (Granger et al., 2005) de-
scribe efficient implementations of arithmetic in fields
of characteristic three for faster pairing computation.
Multi-core implementations of Tate pairing are re-
ported in (Beuchat et al., 2009; Aranha et al., 2010).
(Beuchat et al., 2009) provide an estimate on the op-
timal number of cores needed to compute pairing in a
multi-core environment.
Many low-end processors are released with SIMD
facilities which provide the scope of parallelization
in resource-constrained applications. SIMD-based
implementations of pairing are reported in (Beuchat
et al., 2009; Aranha et al., 2010; Hankerson et al.,
2008). All these data-parallel implementations vec-
torize individual pairing computations, and vary in
their approaches to exploit different SIMD intrinsics
in order to speed up the underlying field arithmetic.
This technique is known as horizontal vectorization.
The other SIMD-based vectorization technique,
vertical vectorization, has also been used for efficient
implementation purposes. (Montgomery, 1991) ap-
plies vertical vectorization to Elliptic Curve Method
(ECM) to factor integers. For RSA implementations
using SSE2 intrinsics, (Page and Smart, 2004) use
two SIMD-based techniques called inter-operation
and intra-operation parallelisms. (Grabher et al.,
2008) propose digit slicing to reduce carry-handling
overhead in the implementation of ate pairing over
Barreto-Naerhig curves defined over prime fields. Im-
plementation results with both inter-pairing and intra-
94
Kr. Bhattacharya A., Das A., Roychowdhury D., Bellur B. and Iyer A..
SIMD-based Implementations of Eta Pairing Over Finite Fields of Small Characteristics.
DOI: 10.5220/0004023000940101
In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 94-101
ISBN: 978-989-8565-24-2
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

pairing parallelism techniques are provided and a
number of implementation strategies are discussed.
Intuitively, so long as different instances of some
computation follow fairly the same sequence of basic
CPU operations, parallelizing multiple instances (ver-
tical vectorization) would be more effective than par-
allelizing each such instance individually (horizontal
vectorization). Computation of eta pairing on curves
over fields of small characteristics appears to be an
ideal setting for vertical vectorization. This is par-
ticularly relevant because all the parties in a standard
elliptic-curve-based protocol typically use the same
curve and the same base point (unlike in RSA where
different entities use different public moduli).
Each of the two vectorization models (horizontal
and vertical) has its private domains of applicability.
Even in the case of pairing computation, vertical vec-
torization does not outperform horizontal vectoriza-
tion in every step. For example, comb-based multipli-
cation (L´opez and Dahab, 2000) of field elements is
expected to be more efficient under vertical vectoriza-
tion than under horizontal vectorization. On the con-
trary, modular reduction using polynomial division
seems to favour horizontal vectorization more than
vertical vectorization, since the number of steps in the
division loop and also the shift amounts depend heav-
ily on the operands. This problem can be bypassed by
using defining polynomials with a small number of
non-zero coefficients (like trinomials or pentanomi-
als). However, computing inverse by the extended
polynomialgcd algorithm cannot be similarly tackled.
Moreover, vertical vectorization is prone to encounter
more cache misses compared to horizontal vectoriza-
tion and even to non-SIMD implementation. The ef-
fects of cache misses are rather pronounced for algo-
rithms based upon lookup tables (like comb methods).
Despite all these potential challenges, vertical
vectorization may be helpful in certain cryptographic
operations. Our experimentation with SSE intrinsics
reveals that this is the case for eta pairing on super-
singular curves over fields of characteristics two and
three. More precisely, horizontal vectorization leads
to speedup between 15–20% over non-SIMD imple-
mentation. Vertical vectorization, on the other hand,
yields an additional 15–25% speedup. In short, the
validation of the effectiveness of vertical vectoriza-
tion in pairing computations is the main technical
contribution of this paper.
The rest of the paper is organized as follows. Sec-
tion 2 reviews the notion of pairing, and lists the algo-
rithms used to implement field and curve arithmetic.
Section 3 describes horizontal and vertical vectoriza-
tion techniques. We also intuitively explain which
of the basic operations are likely to benefit for ver-
tical vectorization compared to horizontal vectoriza-
tion. Our experimental results are tabulated in Sec-
tion 4. We conclude the paper in Section 5 after high-
lighting some potential areas of future research.
2 BACKGROUND ON ETA
PAIRING
In this section, we briefly describe standard algo-
rithms that we have used for implementing arithmetic
in extension fields of characteristics two and three.
We subsequently state Miller’s algorithm for the com-
putation of eta pairing on supersingular curves over
these fields.
2.1 Eta Pairing in a Field of
Characteristic Two
We implemented eta pairing overthe supersingular el-
liptic curve y
2
+ y = x
3
+ x defined over the binary
field F
2
1223
represented as an extension of F
2
by the ir-
reducible polynomial x
1223
+ x
255
+ 1. An element of
F
2
1223
is packed into an array of 64-bit words. The ba-
sic operations on such elements are done as follows.
• Addition: We perform word-level XOR to add
multiple coefficients together.
• Multiplication: Computing products c = ab in
the field is costly, but needed most often in
Miller’s algorithm. Comb-based multiplication
(L´opez and Dahab, 2000) with four-bit windows
is used in our implementations.
• Inverse: We use the extended Euclidean gcd al-
gorithm for polynomials to compute the inverse
of an element in the binary field.
• Square: We use a precomputed table of square
values for all possible 8-bit inputs.
• Square Root: The input element is written as
a(x
2
) + xb(x
2
). Its square root is computed as
a(x) + x
1/2
b(x), where x
1/2
= x
612
+ x
128
.
• Reduction: Since the irreducible polynomial
defining F
2
1223
has only a few non-zero coeffi-
cients, we use a fast reduction algorithm (as in
(Scott, 2007)) for computing remainders modulo
this polynomial.
The embedding degree for the supersingular curve
stated above is four. So we need to work in the
field F
(2
1223
)
4
. This field is represented as a tower
of two quadratic extensions over F
2
1223
. The ba-
sis for this extension is given by (1,u,v,uv), where
g(u) = u
2
+ u + 1 is the irreducible polynomial for
SIMD-basedImplementationsofEtaPairingOverFiniteFieldsofSmallCharacteristics
95

the first extension, and h(v) = v
2
+ v + u defines the
second extension. The distortion map is given by
ψ(x,y) = (x+ u
2
,y+ xu+ v).
Addition in F
(2
1223
)
4
uses the standard word-wise
XOR operation on elements of F
2
1223
. Multiplication
in F
(2
1223
)
4
can be computed by six multiplications in
the field F
2
1223
(Hankerson et al., 2008).
Algorithm 1 describes the computation of eta
pairing η
T
. This is an implementation (Hankerson
et al., 2008) of Miller’s algorithm for the supersin-
gular curve E
2
: y
2
+ y = x
3
+ x under the above rep-
resentation of F
2
1223
and F
(2
1223
)
4
. Here, the point
P ∈ E
2
(F
2
1223
) on the curve has prime order r. Q too
is a point with both coordinates from F
2
1223
. The dis-
tortion map is applied to Q. Algorithm 1 does not
explicitly show this map. The output of the algorithm
is an element of µ
r
, the order-r subgroup of F
∗
(2
1223
)
4
.
Algorithm 1: Eta Pairing Algorithm for a Field of Charac-
teristic Two.
Input: P = (x
1
,y
1
),Q = (x
2
,y
2
) ∈ E(F
2
1223
)[r]
Output: η
T
(P,Q) ∈ µ
r
T ← x
1
+ 1
f ← T ·(x
1
+ x
2
+ 1) + y
1
+ y
2
+ (T + x
2
)u+ v
for i = 1 to 612 do
T ← x
1
x
1
←
√
x
1
,y
1
←
√
y
1
g ←T·(x
1
+x
2
) + y
1
+ y
2
+ x
1
+ 1+ (T+x
2
)u+ v
f ← f ·g
x
2
← x
2
2
,y
2
← y
2
2
end for
return f
(q
2
−1)(q−
√
2q+1)
, where q = 2
1223
.
The complexity of Algorithm 1 is dominated by
the 612 iterations (called Miller iterations), and ex-
ponentiation to the power (q
2
−1)(q−
√
2q+ 1) (re-
ferred to as the final exponentiation). In each Miller
iteration, two square roots, two squares, and seven
multiplications are performed in the field F
2
1223
. In
the entire Miller loop, 1224 square roots and 1224
squares are computed, and the number of multiplica-
tions is 4284. Evidently, the computation of the large
number of multiplications occupies the major portion
of the total computation time. Each multiplication of
F
(2
1223
)
4
(computation of f ·g) is carried out by six
multiplications in F
2
1223
. In these six multiplications,
three variables appear as one of the two operands.
Therefore, only three precomputations (instead of six)
are sufficient for performing all these six multiplica-
tions by the Lopez-Dahab method. For characteristic-
three fields, such a trick is proposed in (Takahashi
et al., 2007). Using Frobenius endomorphism (Scott
et al., 2009; Hankerson et al., 2008), the final expo-
nentiation is computed, so this operation takes only a
small fraction of the total computation time.
2.2 Eta Pairing in a Field of
Characteristic Three
The irreducible polynomial x
509
−x
318
−x
192
+x
127
+
1 defines the extension field F
3
509
. The curve y
2
=
x
3
−x + 1 defined over this field is used. Each ele-
ment of the extension field is represented using two
bit vectors (Smart et al., 2002). The basic operations
on these elements are implemented as follows.
• Addition and Subtraction: We use the formulas
given in (Kawahara et al., 2008).
• Multiplication: Comb-based multiplication (Ah-
madi et al., 2007) with two-bit windows is used in
our implementations.
• Inverse: We use the extended Euclidean gcd al-
gorithm for polynomials to compute the inverse
of an element in the field.
• Cube: We use a precomputed table of cube values
for all possible 8-bit inputs.
• Cube Root: The input element is first written as
a(x
3
) + xb(x
3
) + x
2
c(x
3
). Its cube root is com-
puted as a(x) + x
1/3
b(x) + x
2/3
c(x), where x
1/3
=
x
467
+ x
361
−x
276
+ x
255
+ x
170
+ x
85
, and x
2/3
=
−x
234
+ x
128
−x
43
(Barreto, 2004; Ahmadi et al.,
2007). We have not used the cube-root-friendly
representation of F
3
509
prescribed in (Ahmadi and
Rodriguez-Henriquez, 2010).
• Reduction: We use a fast reduction algorithm
(Scott, 2007) for computing remainders modulo
the irreducible polynomial.
The embedding degree in this case is six, so we
need to work in the field F
(3
509
)
6
. A tower of ex-
tensions over F
3
509
is again used to represent F
(3
509
)
6
.
The first extension is cubic, and is defined by the ir-
reducible polynomial u
3
−u −1. The second exten-
sion is quadratic, and is defined by v
2
+ 1. The basis
of F
(3
509
)
6
over F
3
509
is, therefore, (1,u,u
2
,v,uv, u
2
v).
The distortion map in this case is ψ(x, y) = (u−x,yv).
For multiplying two elements of F
(3
509
)
6
, we have
used 18 multiplications in F
3
509
(Kerins et al., 2005).
The method (Gorla et al., 2007), which uses only 15
such multiplications, is not implemented.
Algorithm 2 describes the computation of eta pair-
ing (Beuchat et al., 2009) in the case of characteristic
three. P and Q are points with both coordinates from
F
3
509
. The distortion map is applied to Q. Algorithm 2
SECRYPT2012-InternationalConferenceonSecurityandCryptography
96

Algorithm 2: Eta Pairing Algorithm for a Field of Charac-
teristic Three.
Input: P = (x
P
,y
P
),Q = (x
Q
,y
Q
) ∈ E(F
3
509
)[r]
Output: η
T
(P,Q) ∈ µ
r
x
P
←
3
√
x
P
+ 1
y
P
← −
3
√
y
P
t ← x
P
+ x
Q
R ← −(y
P
t −y
Q
v−y
P
u)(−t
2
+ y
P
y
Q
v−tu−u
2
)
X
P
[0] ← x
P
,Y
P
[0] ← y
P
X
Q
[0] ← x
Q
,Y
Q
[0] ← y
Q
for i = 1 to 254 do
X
P
[i] ←
3
p
X
P
[i−1]
X
Q
[i] ← X
3
Q
[i−1]
Y
P
[i] ←
3
p
Y
P
[i−1]
Y
Q
[i] ←Y
3
Q
[i−1]
end for
for i = 1 to 127 do
t ← X
P
[2i−1] + X
Q
[2i−1]
w ←Y
P
[2i−1]Y
Q
[2i−1]
t
′
← X
P
[2i] + X
Q
[2i]
w
′
←Y
P
[2i]Y
Q
[2i]
S ←(−t
2
+ wv−tu−u
2
)(−t
′2
+ w
′
v−t
′
u−u
2
)
R ← R·S
end for
return f
(q
3
−1)(q+1)(q+
√
3q+1)
, where q = 3
509
.
does not show this map explicitly. The order of P is a
prime r, and µ
r
is the order-r subgroup of F
∗
(3
509
)
6
.
The first for loop of Algorithm 2 is a precom-
putation loop. The second for loop implements the
Miller iterations. The final exponentiation in the last
line uses Frobenius endomorphism (Scott et al., 2009;
Hankerson et al., 2008). The most time-consuming
operations involved in Algorithm 2 are 508 cubes,
508 cube roots and 3556 multiplications in the field
F
3
509
(given that one multiplication of F
(3
509
)
6
is im-
plemented by 18 multiplications in F
3
509
). The final
exponentiation again does not incur a major compu-
tation overhead in Algorithm 2.
3 HORIZONTAL AND VERTICAL
VECTORIZATION
Many modern CPUs, even in desktop machines, sup-
port a set of data-parallel instructions operating on
SIMD registers. For example, Intel has been releasing
SIMD-enabled CPUs since 1999 (Microsoft, 2010).
As of now, most vendors provide support for 128-bit
SIMD registers and parallel operations on 8-, 16-, 32-
and 64-bit data. We work with Intel’s SSE2 instruc-
tions. Since we use 64-bit words for packing of data,
using these SIMD intrinsics can lead to speedup of
nearly two. In practice, we expect less speedup for
various reasons. First, all steps in a computation do
not possess inherent data parallelism. Second, the in-
put and output values are usually available in chunks
of machine words which are 32 or 64 bits in size. Be-
fore the use of an SIMD instruction, one needs to pack
data stored in normal registers or memory locations
to SIMD registers. Likewise, after using an SIMD in-
struction, one needs to unpack the content of an SIMD
register back to normal registers or memory locations.
Frequent conversion of data between scalar and vec-
tor forms may be costly. Finally, if the algorithm is
memory-intensive, SIMD features do not help much.
We use SIMD-based vectorization techniques for
the computation of eta pairing. These vectorization
techniques provide speedup by reducing the over-
heads due to packing and unpacking. We study two
common SIMD-based vectorization techniques called
horizontal and vertical vectorization. Though vertical
vectorization is capable of reducing data-conversion
overheads substantially, it encounters an increased
memory overhead in terms of cache misses. Ex-
perimental results of eta pairing computation over
fields of characteristics two and three validate the
claim that vertical vectorization achieves better per-
formance gains compared to horizontal vectorization.
3.1 Horizontal Vectorization
Figure 1 explains the working of horizontal vectoriza-
tion. One single operation ⋆ between two multi-word
operands is to be performed. Machine words of indi-
vidual operands are first packed into SIMD registers,
and one SIMD instruction for ⋆ is used to compute the
output in a single SIMD register. The result stored
in the output SIMD registers can further be used in
remaining computations. With 64-bit words packed
two at a time in 128-bit SIMD registers, this use of
SIMD instructions is expected to let the operation fin-
ish using half of as many clock cycles as are needed
by normal 64-bit registers.
As an example, consider operands a and b each
stored in an array of sixteen 64-bit words. Suppose
that we need to compute the bit-wise XOR of a and
b, and store the result in c. A usual 64-bit imple-
mentation calls for sixteen invocations of the CPU
instruction for XOR. SIMD-based XOR handles 128
bits of the operands in one CPU instruction, and fin-
ishes after only eight invocations of this instruction.
The output array c of SIMD registers is available in
the packed format required in future data-parallel op-
SIMD-basedImplementationsofEtaPairingOverFiniteFieldsofSmallCharacteristics
97

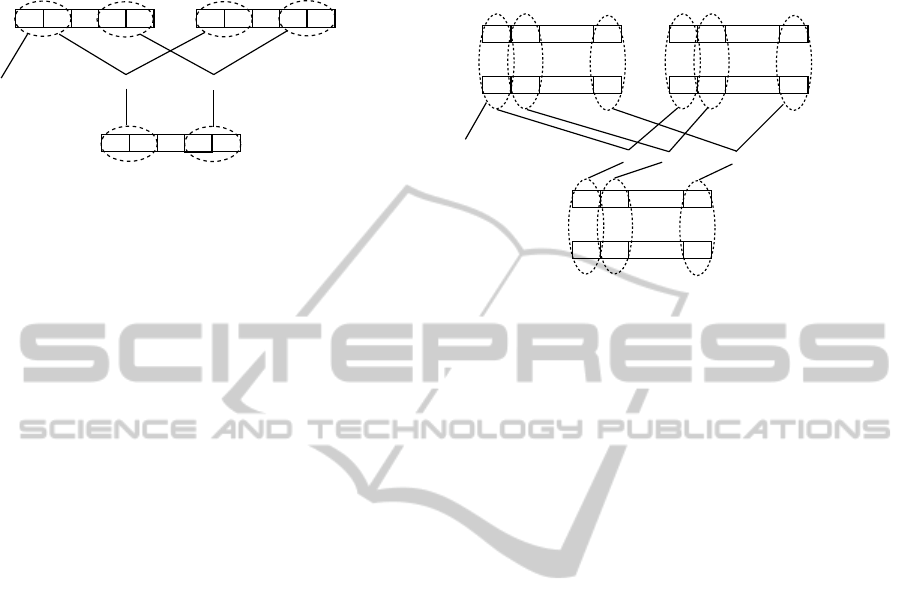
erations in which c is an input.
★ ★
. . .
. . .
. . .
Operand 1 Operand 2
Packing
SIMD operation
Result
Input
Instance
Figure 1: Horizontal vectorization.
There are, however, situations where horizontal
vectorization requires unpacking of data after a CPU
instruction. Consider the unary left-shift operation on
an array a of sixteen 64-bit words. Let us index the
words of a as a
1
,a
2
,...,a
16
. The words a
2i−1
and
a
2i
are packed into an SIMD register R
i
. Currently,
SIMD intrinsics do not provide facilities for shifting
R
i
as a 128-bit value by any amount (only byte-level
shifts are allowed). What we instead obtain in the out-
put SIMD register is a 128-bit value in which both the
64-bit components are individually left-shifted. The
void created in the shifted version of a
2i−1
needs to be
filled by the most significant bits of the pre-shift value
of a
2i
. More frustratingly, the void created in a
2i
by
the shift needs to be filled by the most significant bits
of the pre-shift value of a
2i+1
which is a 64-bit mem-
ber of a separate SIMD register R
i+1
. The other 64-bit
member a
2i+2
packed in R
i+1
must not interfere with
the shifted value of R
i
. Masking out a
2i+2
from R
i+1
eats up a clock cycle, and is, in principle, same as
unpacking. To sum up, horizontal vectorization may
result in frequent scalar-to-vector and vector-to-scalar
conversions, and suffer from huge packing and un-
packing overheads.
3.2 Vertical Vectorization
Vertical vectorization works as shown in Figure 2.
Two instances of the same operation are carried out on
two different sets of data. Data of matching operands
from the two instances are packed into SIMD reg-
isters, and the same sequence of operations is per-
formed on these registers using SIMD intrinsics. For
each SIMD register, half of its data pertains to one
instance, and the remaining half to the other instance.
After each SIMD instruction, half of the output SIMD
register contains the result for the first instance, and
the remaining half the result for the second instance.
Thus, data from two separate instances are maintained
in 64-bit formats in these SIMD registers throughout
a sequence of operations. When the sequence is com-
pleted, data from the final output SIMD registers are
unpacked into the respective64-bit storage outputs for
the two instances.
★ ★ ★
Operand 2
. . .
. . .
. . .
. . .
. . .
. . .
Operand 1
SIMD operation
Instance 2
Instance 1
Result 1
Result 2
Packing
Figure 2: Vertical vectorization.
The advantage of this vectorization technique is
that it adapts naturally to any situation where two
identical sequences of operations are performed on
two separate sets of data. The algorithm does not need
to possess inherent data parallelism. However, the
sequence of operations must be identical (or nearly
identical) on two different sets of data. Finally, a
computation using vertical vectorization does not re-
quire data conversion after every SIMD operation in
the CPU, that is, potentially excessive packing and
unpacking overheads associated with horizontal vec-
torization are significantly eliminated.
Let us now explain how vertical vectorization gets
rid of the unpacking requirement after a left-shift op-
eration. Suppose that two operands a and b need to be
left-shifted individually by the same number of bits.
The i-th words a
i
and b
i
are packed in an SIMD reg-
ister R
i
. First, a suitably right-shifted version of R
i
is stored in another SIMD register S
i
. After that, R
i
is
left-shifted by a single SIMD instruction causing both
a
i
and b
i
to be left-shifted individually. This shifted
SIMD register is then XOR-ed with the SIMD regis-
ter S
i
. The individual 64-bit words a
i+1
and b
i+1
are
not needed in the unpacked form.
3.3 Vectorization of Eta Pairing
Eta pairing on supersingular curves defined over fields
of characteristics two and three can be computed us-
ing bit-wise operations only (that is, no arithmetic op-
erations are needed). More precisely, only the XOR,
OR, AND, and the left- and right-shift operations on
64-bit words are required. As explained earlier, both
horizontal and vertical vectorizations behave grace-
fully for the XOR, OR and AND operations. On
the contrary, shift operations are efficient with ver-
tical vectorization only. Therefore, the presence and
SECRYPT2012-InternationalConferenceonSecurityandCryptography
98

importance of shift operations largely determine the
relative performance of the two vectorization meth-
ods. We now study each individual field operation (in
F
2
1223
or F
3
509
) in this respect.
• Addition/Subtraction: Only XOR, OR and
AND operations are needed to carry out addition
and subtraction of two elements in both types of
fields. So both the vectorization models are suit-
able for these operations.
• Multiplication (without Reduction): We use
comb-based multiplication algorithms in which
both left- and right-shift operations play a cru-
cial role. Consequently, multiplication should
be faster for vertical vectorization than horizontal
vectorization.
• Square/Cube (without Reduction): Since we
have used precomputations in eight-bit chunks,
byte-level shifts suffice, that is, both models of
vectorization are efficient for these operations.
• Modular Reduction: Reduction using the cho-
sen irreducible polynomials call for bit-level shift
operations, so vertical vectorization is favoured.
• Square-root/Cube-root with Modular Reduc-
tion: Extraction of the polynomials a,b (and c for
characteristic three), and multiplication by x
1/2
(or x
1/3
and x
2/3
) involve several shift operations.
So vertical vectorization seems to be the better
choice.
• Inverse: The extended Euclidean algorithm is
problematic for both horizontal and vertical vec-
torization models. On one hand, bit-level shifts
impair the performance of horizontal vectoriza-
tion. On the other hand, the sequence for a gcd
calculation depends heavily on the operands, ren-
dering vertical vectorization infeasible to imple-
ment. We, therefore, use only non-SIMD imple-
mentations for the inverse operation.
Multiplication (with modular reduction) happens
to be the most frequent operation in Algorithms 1 and
2. Vertical vectorization is, therefore, expected to out-
perform horizontal vectorization for these algorithms.
4 EXPERIMENTAL RESULTS
We implement eta pairing on supersingular elliptic
curves defined over fields of characteristics two and
three. SSE2 intrinsics of Intel Xeon E5410 2.33 GHz
processor are used in our 64-bit C implementations.
We measure the timing of field operations and pair-
ing computation with the -O2 optimization flag of the
gcc 4.3.2 compiler. The timing results are reported
in clock cycles. For non-SIMD and horizontal-SIMD
implementations, the timings correspond to the exe-
cution of one field operation or one eta-pairing com-
putation. For the vertical-SIMD implementation, two
operations are performed in parallel. The times ob-
tained by our implementation are divided by two in
the tables below in order to indicate the average time
per operation. This is done to make the results directly
comparable with the results from the non-SIMD and
horizontal-SIMD implementations. We use gprof and
valgrind to profile our program. Special cares are
adopted to minimize cache misses (Drepper, 2007).
Table 1: Timing for field operations in F
2
1223
(clock cycles).
Mode Add Mult
∗
Sqr
∗
Sqrt
∗
Non-SIMD 44.5 16098.2 471.3 2831
SIMD (H) 21.2 13019.4 534.8 3051.2
SIMD (V) 21.7 9587.9 445.9 2253.7
Ref 1 8200 600 500
Ref 2 5438.4 480 748.8
Ref 3 4030 160 166
∗
Including modular reduction
Ref 1 (Hankerson et al., 2008)
Ref 2 (Beuchat et al., 2009)
Ref 3 (Aranha et al., 2010)
Table 2: Timing for field operations in F
3
509
(clock cycles).
Mode Add Mult
∗
Cube
∗
Cube root
∗
Non-SIMD 38.1 14277.6 946.8 5769.9
SIMD (H) 22.2 12071.5 1045.3 5833.5
SIMD (V) 19.1 10002 785.8 4130.1
Ref 1 7700 900 1200
Ref 2 4128 900 974.4
∗
Including modular reduction
Ref 1 (Hankerson et al., 2008)
Ref 2 (Beuchat et al., 2009)
Tables 1 and 2 summarize the average computa-
tion times of basic field operations in F
2
1223
and F
3
509
.
For the addition and multiplication operations, both
types of SIMD-based implementations perform better
than the non-SIMD implementation. For the square,
square-root, cube and cube-root operations, the per-
formance of the horizontal implementation is slightly
poorer than that of the non-SIMD implementation,
whereas the performance of the vertical implementa-
tion is noticeably better than that of the non-SIMD
implementation. The experimental results tally with
our theoretical observations discussed in Section 3.3.
That is, field operations involving bit-level shifts sig-
nificantly benefit from the vertical model of vector-
ization. In particular, the time of each multiplication
operation can be reduced by 10–20% using horizontal
vectorization. For vertical vectorization, this reduc-
tion is in the range 30–40%.
In Table 3, we mention the average times for
computing one eta pairing for non-SIMD, horizontal-
SIMD-basedImplementationsofEtaPairingOverFiniteFieldsofSmallCharacteristics
99

Table 3: Times for computing one eta pairing (in millions
of clock cycles).
Mode Characteristic Time Speedup
Non-SIMD
2 75.2
3 59.4
SIMD (H)
2 62.2 17.3%
3 50.8 14.5%
SIMD (V)
2 41.9 44.3%
3 42.8 27.9%
Ref 1
2 39
3 33
Ref 2
2 26.86
3 22.01
Ref 3 2 18.76
Ref 1 (Hankerson et al., 2008)
Ref 2 (Beuchat et al., 2009)
Ref 3 (Aranha et al., 2010)
SIMD and vertical-SIMD implementations. The
speedup figures tabulated are with respect to the
non-SIMD implementation. Vertical vectorization is
seen to significantly outperform both non-SIMD and
horizontal-SIMD implementations.
In Tables 1–3, we also mention other reported
implementation results on finite-field arithmetic and
eta-pairing computation. Our implementations are
slower than these three reported implementations. In
fact, these works make use of higher SSE features,
whereas we have used only SSE2 intrinsics. The pa-
pers (Beuchat et al., 2009; Aranha et al., 2010) also
report multi-threaded implementations of eta pairing
which our work does not deal with. The timings given
in the above tables correspond to single threads only.
The main objective of our work is to compare hori-
zontal vectorization with vertical vectorization for the
implementation of eta pairing over fields of character-
istics two and three. Moreover, we have not used ad-
vanced SIMD features. To this extent, our experimen-
tal results, although slower than the best reported im-
plementations, appear to have served our objectives.
How vertical vectorization performs for (Hankerson
et al., 2008; Beuchat et al., 2009; Aranha et al., 2010)
continues to remain an open research problem.
5 CONCLUSIONS
In this paper, we focus on efficient SIMD-based soft-
ware implementations of eta pairing on supersingu-
lar elliptic curves over fields of characteristics two
and three. Horizontal and vertical vectorization tech-
niques are studied, and our implementation results es-
tablish the superiority of vertical vectorization over
horizontal vectorization in the context of eta pair-
ing computations over fields of small characteristics.
Some possible extensions of our work are stated now.
• We have studied the two vectorization models for
bit-wise operations only. It is unclear how the
two models compare when arithmetic operations
are involved. For example, eta pairing on ellip-
tic curves defined over prime fields heavily use
multiple-precision integer arithmetic. Other types
of pairing (on ordinary curves) and even other
cryptographic primitives(like DSA in prime fields
and RSA under common moduli) also require in-
teger arithmetic. Managing carries and borrows
during addition and subtraction stands in the way
of effective vectorization. Multiplication poses a
more potent threat to data-parallelism ideas.
• We have used only the SSE2 intrinsics set, chiefly
because of its wide availability. It is worthwhile
to investigate the impacts of exploiting additional
features supplied by higher SSE versions. One
may also use other intrinsics sets (like IBM’s Al-
tiVec and AMD’s 3DNow!) to compare two mod-
els of vectorization.
• GPUs, although not as common and cheap as
SIMD registers, constitute an emerging platform
for vectorizing pairing computations. Distribut-
ing computations among GPU threads and asso-
ciated memory-management issues (like packing
operands in arrays instead of SIMD registers) are
substantially different from the type of experi-
ments we have reported in this paper. The max-
imum parallelizability of eta pairing under hor-
izontal vectorization in the context of GPUs is
limited by the size of the operands. On the con-
trary, vertical vectorization imposes no such re-
strictions, and is capable of making eta pairing ar-
bitrarily parallelizable, at least in theory. A prac-
tical validation of this claim is another area that
merits research attention.
REFERENCES
Ahmadi, O., Hankerson, D., and Menezes, A. (2007). Soft-
ware Implementation of Arithmetic in F
3
m
. In Inter-
national Workshop on the Arithmetic of Finite Fields
(WAIFI 2007), pages 85–102.
Ahmadi, O. and Rodriguez-Henriquez, F. (2010). Low
Complexity Cubing and Cube Root Computation over
F
3
m
in Polynomial Basis. IEEE Transactions on Com-
puters, 59:1297–1308.
Aranha, D. F., L´opez, J., and Hankerson, D. (2010). High-
Speed Parallel Software Implementation of the η
T
Pairing. In CT-RSA 2010, pages 89–105.
Barreto, P. S. L. M. (2004). A Note on Efficient Computa-
tion of Cube Roots in Characteristic 3. In IACR Eprint
Archive. http://eprint.iacr.org/2004/305.
SECRYPT2012-InternationalConferenceonSecurityandCryptography
100

Barreto, P. S. L. M., Galbraith, S. D., O
´
Eigeartaigh, C., and
Scott, M. (2007). Efficient Pairing Computation on
Supersingular Abelian Varieties. Designs, Codes and
Cryptography, 42(3):239–271.
Barreto, P. S. L. M., Kim, H. Y., Lynn, B., and Scott, M.
(2002). Efficient Algorithms for Pairing-Based Cryp-
tosystems. In CRYPTO 2002, pages 354–368.
Beuchat, J.-L., L´opez-Trejo, E., Mart´ınez-Ramos, L., Mit-
sunari, S., and Rodrguez-Henr´ıquez, F. (2009). Multi-
core Implementation of the Tate Pairing over Super-
singular Elliptic Curves. In Cryptology and Network
Security, pages 413–432.
Boneh, D. and Franklin, M. K. (2001). Identity-Based En-
cryption from the Weil Pairing. In CRYPTO 2001,
pages 213–229.
Boneh, D., Lynn, B., and Shacham, H. (2004). Short Sig-
natures from the Weil Pairing. Journal of Cryptology,
17:297–319.
Drepper, U. (2007). What Every Programmer Should Know
About Memory. http://lwn.net/Articles/250967/.
Freeman, D., Scott, M., and Teske, E. (2010). A Taxon-
omy of Pairing-Friendly Elliptic Curves. Journal of
Cryptology, 23:224–280.
Gorla, E., Puttmann, C., and Shokrollahi, J.
(2007). Explicit Formulas for Efficient Mul-
tiplication in F
3
6m
. In SAC, pages 173–183.
http://portal.acm.org/citation.cfm?id=1784881.17848
93.
Grabher, P., Großsch¨adl, J., and Page, D. (2008). On Soft-
ware Parallel Implementation of Cryptographic Pair-
ings. In SAC, pages 35–50.
Granger, R., Page, D., and Stam, M. (2005). Hardware and
Software Normal Basis Arithmetic for Pairing-Based
Cryptography in Characteristic Three. IEEE Trans.
Computers, 54(7):852–860.
Hankerson, D., Menezes, A., and Scott, M. (2008). Soft-
ware Implementation of Pairings. In Identity Based
Cryptography, pages 188–206. IOS Press.
Hess, F., Smart, N. P., and Vercauteren, F. (2006). The Eta
Pairing Revisited. IEEE Transactions on Information
Theory, 52(10):4595–4602.
Joux, A. (2004). A One Round Protocol for Tripartite
Diffie-Hellman. Journal of Cryptology, 17:263–276.
Kawahara, Y., Aoki, K., and Takagi, T. (2008). Faster
Implementation of η
T
Pairing over GF(3
m
) Using
Minimum Number of Logical Instructions for GF(3)-
Addition. In Pairing, pages 282–296.
Kerins, T., Marnane, W. P., Popovici, E. M., Barreto, P. S.
L. M., and Brazil, S. P. (2005). Efficient Hardware For
The Tate Pairing Calculation In Characteristic Three.
In CHES, pages 412–426.
Lee, E., Lee, H. S., and Park, C. M. (2009). Efficient
and Generalized Pairing Computation on Abelian Va-
rieties. IEEE Transactions on Information Theory,
55:1793–1803.
L´opez, J. and Dahab, R. (2000). High Speed Software Im-
plementation in F
2
m
. In Indocrypt 2000, LNCS, pages
93–102.
Microsoft (2010). MMX, SSE, and SSE2 Intrinsics.
http://msdn.microsoft.com/en-us/library/y0dh78ez.
Miller, V. (2004). The Weil Pairing and Its Efficient Calcu-
lation. Journal of Cryptology, 17:235–261.
Montgomery, P. L. (1991). Vectorization of the Elliptic
Curve Method. ACM.
Page, D. and Smart, N. P. (2004). Parallel Crypto-
graphic Arithmetic Using a Redundant Montgomery
Representation. IEEE Transactions on Computers,
53:1474–1482.
Scott, M. (2007). Optimal Irreducible Polynomials
for GF(2
m
) Arithmetic. In IACR Eprint Archive.
http://eprint.iacr.org/2007/192.
Scott, M., Benger, N., Charlemagne, M., Perez, L. J. D., and
Kachisa, E. J. (2009). On the Final Exponentiation
for Calculating Pairings on Ordinary Elliptic Curves.
In Pairing-Based Cryptography Pairing 2009, LNCS,
pages 78–88.
Smart, N. P., Harrison, K., and Page, D. (2002). Soft-
ware Implementation of Finite Fields of Characteristic
Three. LMS Journal Computation and Mathematics,
5:181–193.
Takahashi, G., Hoshino, F., and Kobayashi, T.
(2007). Efficient GF(3
m
) Multiplication Algo-
rithm for η
T
Pairing. In IACR Eprint Archive.
http://eprint.iacr.org/2007/463.
Vercauteren, F. (2010). Optimal Pairings. IEEE Transac-
tions on Information Theory, 56:455–461.
SIMD-basedImplementationsofEtaPairingOverFiniteFieldsofSmallCharacteristics
101