
Sphere Decoding Complexity Reduction using an Adaptive SD-OSIC
Algorithm
Bora Kim, Sangmi Moon, Saransh Malik, Cheolhong Kim and Intae Hwang
Department of Electronics and Computer Engineering, Chonnam National University,
300 Yongbong-Dong, Buk-Gu, Gwangju, Republic of Korea
Keywords: Link Adaptation, MIMO, OSIC, SNR, Sphere Decoding.
Abstract: Sphere decoding is a technique able to achieve the optimal performance of the maximum likelihood
decoder, but its high and variable complexity can make the practical implementation infeasible. In this
paper, we present an adaptive system, called adaptive SD-OSIC, as a way of reducing the decoding
complexity while maintaining the error performance of conventional sphere decoding.
1 INTRODUCTION
OPTIMAL maximum likelihood (ML) decoding
measures the distance from the received vector to
all possible codewords in the lattice, but if we use a
multiple-input multiple-output (MIMO) system with
transmit antennas, and modulation of
2
constellation points, where is the number of bits
per symbol, the number of possibilities for vector
that should be tested becomes 2
. In 1999,
Viterbo and Boutros (Viterbos and Boutros, 1999)
proposed a universal lattice decoding technique, now
known as sphere decoding (SD), which achieves the
error performance of ML, but simplifies the search
by restricting it to codewords that lie inside a sphere
centered at the received signal vector. SD algorithm
is less complex than the conventional ML, but the
number of operations that must be performed varies
with the SNR and channel conditions; therefore,
suboptimal decoding techniques, such as zero
forcing (ZF), minimum mean-square error (MMSE),
and ordered successive interference cancelation
(OSIC) are usually preferred as they are easier to
implement in hardware.
Among the recent attempts to reduce SD
complexity are hybrid SD-ZF (Lee and Kim, 2006),
K-best (Viterbos and Boutros, 1999) and fixed SD
(FSD) (Guo and Nilsson, 2006); (Barbero and
Thompson); the last two techniques achieve a
constant number of iterations independent of the
SNR or channel conditions, but exhibit a tradeoff
between the bit error rate (BER) performance and
computational cost; while the former one proposes
reducing the search operations performed by SD by
decoding the symbols with high SNR using ZF.
In this paper, we propose to reduce the number
of iterations needed by conventional SD and
improve the concept presented in (Lee and Kim,
2006) by combining SD, OSIC, and the principle of
link adaptation. The resulting system achieves a very
low, quasi-constant complexity over the entire SNR
range, exhibits better error performance than SD and
OSIC at a low SNR, and makes a minimum sacrifice
of BER at a high SNR.
This paper is divided as follows: Sections II and
III explain the SD algorithm and the Adaptive SD-
OSIC system, respectively; Section IV presents and
discusses the simulation results; and, in Section V,
we present our conclusions.
Figure 1: Graphic representation of the SD concept.
2 SD ALGORITHM
In a MIMO system with
transmit antennas and
75
Kim B., Moon S., Malik S., Kim C. and Hwang I..
Sphere Decoding Complexity Reduction using an Adaptive SD-OSIC Algorithm.
DOI: 10.5220/0004027200750080
In Proceedings of the International Conference on Signal Processing and Multimedia Applications and Wireless Information Networks and Systems
(SIGMAP-2012), pages 75-80
ISBN: 978-989-8565-25-9
Copyright
c
2012 SCITEPRESS (Science and Technology Publications, Lda.)

receive antennas, the
×1 received signal vector
can be expressed using equation (1):
=+
(1)
where H is the
×
channel matrix, x represents
the
×1 transmitted vector, and n represents the
×1 noise matrix.
To perform SD, the complex matrices and
vectors are decomposed into real values:
=
(2)
M=
−
(3)
=
(4)
=
(5)
When searching for a candidate to be the transmitted
vector, SD selects the codeword that minimizes the
metric (6).
‖−‖
(6)
The SD algorithm requires applying (6) only over
the codewords or lattice points that are inside a
sphere of initial radius =
√
, centered at the
received signal vector y. Each time a valid point is
found, the radius of the sphere is reduced further
until there is only one lattice point inside the sphere.
After the real decomposition, equation (6) can be
expressed as:
‖
−
‖
(7)
To perform the SD algorithm, it is necessary to
estimate the values of the received signal vector by
applying a simple decoding technique such as ZF or
MMSE. In our research, we decided to work
exclusively with MMSE, since it offers the same
BER performance as ZF, with an additional
advantage in complexity (Zimmermann et al.). The
MMSE estimation is given by equation (8):
=
(8)
where
=
+
Now, equation (7) can be expressed in terms of the
estimated vector ρ:
‖−‖
=‖(−)‖
+‖‖
−‖‖
(9)
Based on (9), we deduce that one necessary
condition for any codeword or lattice point to lie
inside a sphere of radius d is:
d
>‖(−)‖
(10)
>(−)
(−)
If we apply the Cholesky factorization to the
matrix
, we obtain the 2N
×2N
upper
triangular matrix R; and then, we can express
equation (10) as:
>
(
−
)
(
−
)
>
(
,
)
(
)
(
−
)
+
(
,
)
(
,
)
−
(
)
>
(
,
)
(
−
)
+
(
,
)
(
)
−
(
)
+
(
,
)
(
,
)
(
−
)
+⋯
where =2
.
In SD we search for the most accurate value of
each of the m components of vector s. The algorithm
starts searching the points in descending order, from
= to=1. The number of possible values of
is determined by the calculation of the lower and
upper bounds:
−
(
,
)
≤
̂
≤
+
(
,
)
(11)
where
rounds to the largest possible integer and
rounds to the smallest possible integer.
For i= the radius
is set to the initial value
√
and we center the search around the
MMSE
estimated value
; therefore, we set
=
. For
the other values of , the radius
and
are
calculated with the equations:
(
)
>
−
(
,
)
(
−
)
(12)
(
)
=
(
)
−
(
,
)
(
,
)
−
(13)
After calculating the upper and lower bounds, the
options for ̂
are sorted in ascending order,
according to the Euclidean distance to
, which
increases the possibility of finding the accurate
answer during the first iterations (Chan and Lee,
2002); (Noording et al.).
When =1, we estimate a new radius,
=
−
+
,
(
−
)
(14)
If this new radius is smaller than the previous initial
radius, i.e., if it fulfills the condition
<
, then,
the estimated vector ̂ is stored and becomes a
strong candidate for possessing the actual
transmitted values. If the condition above is not
satisfied, the algorithm will try other options for the
members of̂, starting witĥ
, until there are no
SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications
76

more points to evaluate inside the sphere. Then, it
will output the last stored vector ̂.
Figure 2: Architecture of the adaptive SD-OSIC system.
3 ADAPTIVE SD-OSIC SYSTEM
The system we propose aims to improve the
complexity of SD by combining it with OSIC and
the link adaptation principle. The hybrid SD-ZF
system proposed in (Lee and Kim, 2006) uses a
simple noise estimation based on the ZF pre-
decoded symbols. In our case, we use the OSIC
algorithm to estimate noise considering the channel
interference and canceling the interference from the
decoded symbols, yielding better results in terms of
BER. Below, we show the OSIC algorithm, where
the components of the received vector with the best
channel conditions are decoded with priority and
subtracted from the vector y until all symbols are
decoded.
In a low SNR region, where the SD performs the
highest number of iterations, our system uses OSIC
to decode the symbols influenced by a favorable
channel response and decodes the rest using the
modified SD algorithm based on the work of Chan
& Lee (Chan and Lee, 2002). The nature of OSIC
guarantees an enhancement in the BER performance
while reducing complexity. On the other hand, as the
SNR increases, the number of computations needed
by SD decreases and tends to be constant. Therefore,
a combination of SD and OSIC for a very high SNR
would degrade the BER performance of
conventional SD and would not offer a great
advantage in complexity. Thus, we decided to use
the link adaptation principle, which allows us to
combine SD and OSIC only for low and middle
SNR, and apply SD exclusively for high SNR,
which yields very low, quasi-constant complexity
over the entire SNR range.
OSIC algorithm.
∶,,
↓
=
+
↓
for=1∶
=
(
)
=
(
,:
)
̂
=
→
(
.
)
=−̂
(
:,
)
(
:,
)
=0
=
+
end
4 SIMULATION RESULTS
In this section, we analyze the performance of
MATLAB simulations based on the parameters
shown in Table 1. The performance is measured in
terms of BER and elapsed time (complexity). Prior
to MATLAB version 6, the function 'flops' was used
to count the number of floating point operations
executed by an algorithm. The latest versions of
MATLAB, we use the commands ‘tic’ and ‘toc’ to
measure the complexity of an algorithm. These
commands measure the time it takes the MATLAB
software to execute one or more lines of MATLAB
code.
Figure 3 and 4 shows the BER and complexity
performance of hybrid SD-OSIC vs. hybrid SD-ZF
systems, respectively; the number in parenthesis
indicates the number of symbols decoded by OSIC
or ZF. Because hybrid SD-OSIC uses MMSE as pre-
decoding technique and no matrix decomposition is
required for OSIC, the complexity performance
between hybrid SD-OSIC and hybrid SD-ZF is very
similar; however, as explained in section 3, better
results in error performance are obtained with hybrid
SD-OSIC.
Table 1: Simulation parameters.
MIMO technique SM
No. of antennas 4x4
Modulation 16 QAM
Coding rate none
Pre-detection MMSE
Detection SD and OSIC
SphereDecodingComplexityReductionusinganAdaptiveSD-OSICAlgorithm
77
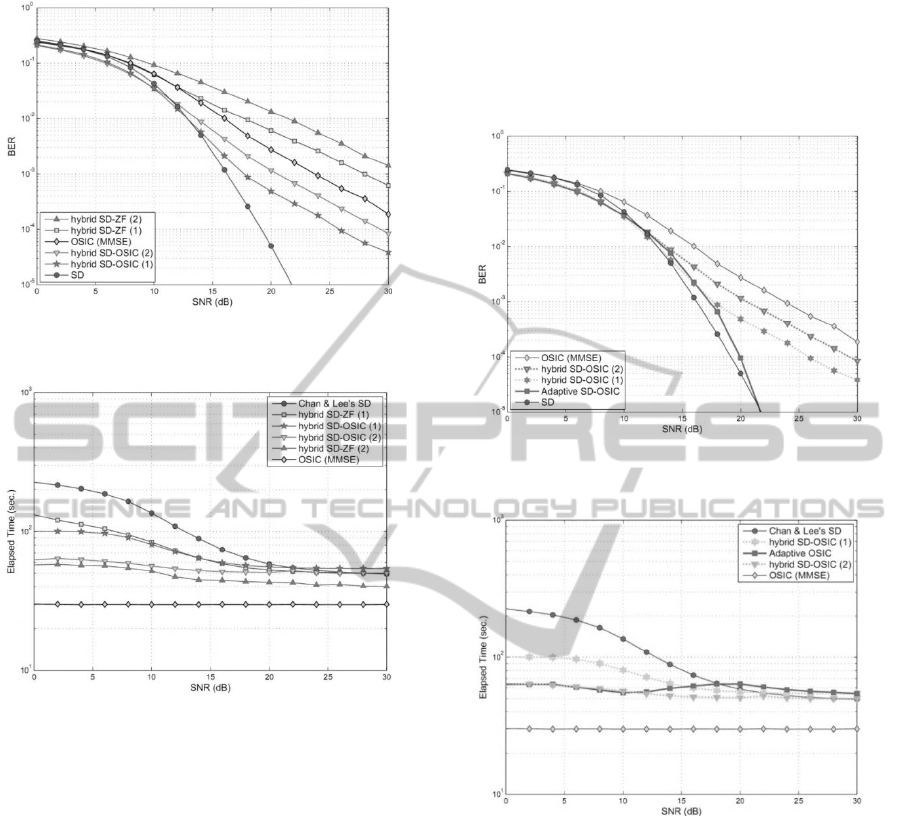
Figure 3: BER performance of hybrid SD-OSIC vs. SD,
OSIC, and hybrid SD-ZF.
Figure 4: Complexity performance of hybrid SD-OSIC vs.
SD, OSIC, and hybrid SD-ZF.
In Figure 3, we can also observe the BER
performance of conventional SD (the original and
Chan & Lee's SD produce exactly the same BER),
vs. the BER performance of hybrid SD-OSIC. At a
low SNR, the hybrid systems exhibit better BER
performance than SD and OSIC. The reason for this
is that in SD, the last levels of the tree search have
more points to be compared with, this make those
levels less susceptible to noise. In the conventional
SD algorithm the elements of the received vector are
not ordered according to noise or channel condition;
hence, the elements with more noise can be found at
the beginning or at the end of the “tree branches”.
But by using OSIC, we guarantee that the elements
that are most affected by noise are decoded with SD;
this can be similar to moving them forward in the
tree levels. In addition, because OSIC is also a very
efficient algorithm, the symbols decoded by OSIC
contribute to enhance the performance at low SNR.
When SNR reaches values higher than 12 or 14 dB
using hybrids SD-OSIC (2) and (1), respectively, the
hybrid scheme exhibits BER performance inferior to
that of conventional SD. At high SNR, hybrids SD-
OSIC (1) and (2) do not achieve the BER
performance of ML, but they are approximately 3
and 6 dB better than conventional OSIC (MMSE),
respectively.
Figure 5: BER performance of the adaptive SD-OSIC
system vs. SD, OSIC, and hybrid SD-OSIC schemes.
Figure 6: Complexity performance of the adaptive SD-
OSIC system vs. SD, OSIC, and hybrid SD-OSIC schemes.
In Figure 4, we can verify that for hybrid SD-
OSIC (2) the number of iterations is significantly
reduced in the low SNR region. Hybrid SD-OSIC
(1) shows a slightly higher complexity compared to
hybrid SD-OSIC (2); however, the performance is
better if we compare it to Chan & Lee's SD. We also
observe that for very good SNR the number of
iterations needed by SD and the hybrid algorithms
become constant. Based on the simulation results
shown in Figure 3 and 4 and considering the
complexity-BER tradeoff, we set the SNR thresholds
for the adaptive SD-OSIC system. For very low
SNR (≤14), the system chooses hybrid
SD-OSIC (2), which allows fast symbol decoding;
for midrange SNR (14<<18),the
SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications
78
system selects hybrid SD-OSIC (1); and finally, for
high SNR(≥18), it chooses only Chan &
Lee's SD.
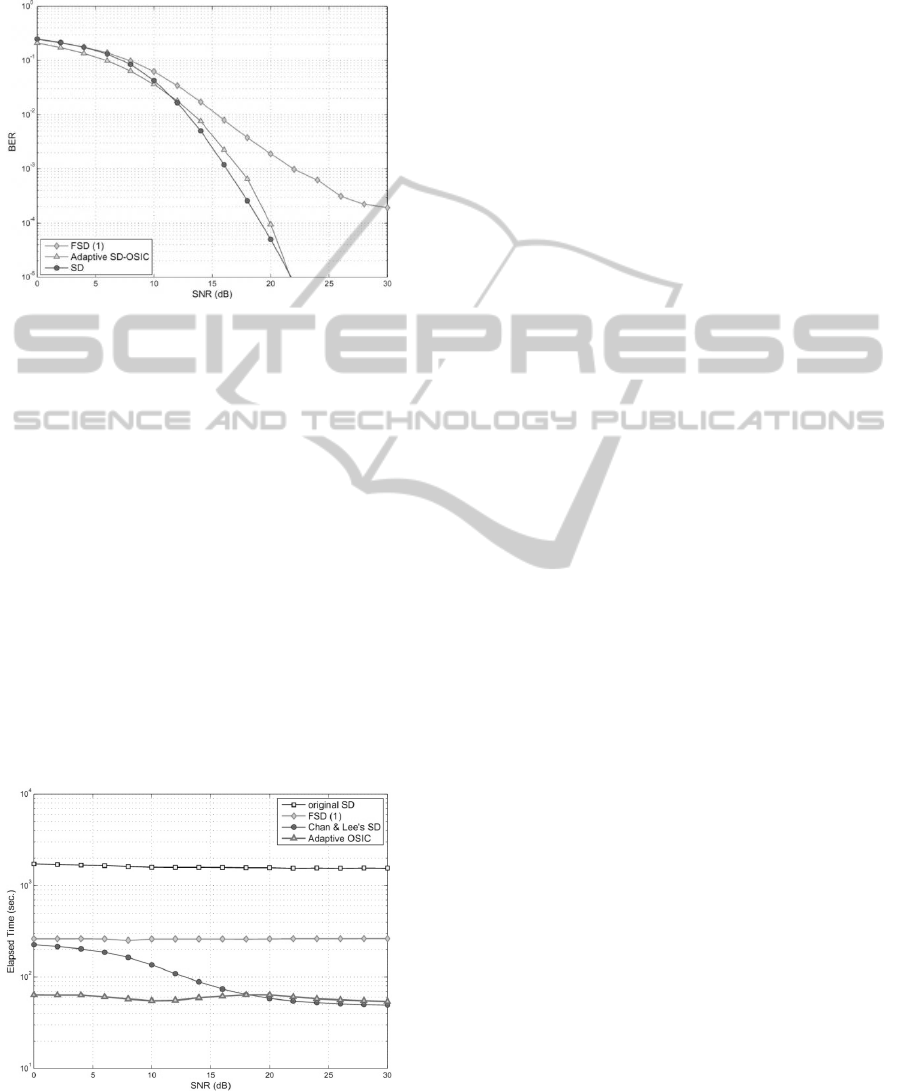
Figure 7: BER performance of the adaptive SD-OSIC
system vs. FSD (1)
Figure 5 shows the BER performance of the
proposed adaptive SD-OSIC system. As in the
MIMO closed loop, the SNR is estimated at the
receiver; however, this information is not sent to the
transmitter; instead, it is used to choose the scheme
according to the SNR threshold.
Figure 6 shows that the adaptive SD-OSIC
system achieves a significant improvement in
average complexity compared to conventional SD
algorithms. Currently, we are working on optimizing
the SD-OSIC system to achieve a fixed number of
iterations.
Figure 7 and 8 show the performance of the
adaptive SD-OSIC system vs. FSD. The scheme
proposed in (Lee and Kim, 2006) and (Guo and
Nilsson, 2006) was originally simulated using the
complex version of SD.
Figure 8: Complexity performance of the adaptive SD-
OSIC system vs. FSD (1).
However, the same algorithm is applicable when
we use matrix decomposition. In our simulation, the
symbol with worst SNR is allocated in the last level
of the tree search which contains all the possible
options according to the modulation scheme; the
other levels contain only the symbol decoded using
OSIC. This way, it is possible to fix the iterations
using by SD. In other words, FSD is a SD algorithm
where the radius of the sphere does not shrink and
the same amount of codewords is evaluated
regardless of the SNR. As we can see in Figure 8,
FSD exhibits constant complexity; however such
complexity can be even greater than that of
conventional SD.
5 CONCLUSIONS
In this paper, we proposed an adaptive SD-OSIC
system that achieves better performance than
conventional SD algorithms. One important feature
of the proposed system is that it exhibits quasi-
constant complexity through the entire SNR range,
which provides better throughput performance.
Unlike other proposed algorithms, our system
reduces and improves the complexity of the
conventional SD, with little sacrifice of BER in high
SNR regions. Furthermore, for low SNR, our system
achieves better BER performance than conventional
SD and OSIC algorithms.
ACKNOWLEDGEMENTS
This research was supported by the MKE(The
Ministry of Knowledge Economy), Korea, under the
ITRC(Information Technology Research Center)
support program supervised by the NIPA(National
IT Industry Promotion Agency) (NIPA-2012-
H0301-12-3005). This study was financially
supported by Chonnam National University, 2011.
REFERENCES
E. Viterbo, J. Boutros, "A Universal Lattice Code Decoder
for Fading Channels," IEEE Transactions on
Information Theory, vol.45, no.5, July 1999.
Hong-Ju Lee; Dongwoo Kim, "A Hybrid Zero-Forcing
and Sphere-Decoding Method for MIMO Systems",
Wireless Communications, Networking and Mobile
Computing, 2006. WiCOM 2006.
Z. Guo, P. Nilsson, "Algorithm and Implementation of the
K-Best Sphere Decoding for MIMO Detection," IEEE
SphereDecodingComplexityReductionusinganAdaptiveSD-OSICAlgorithm
79

Journal on Selected Areas in Communications, vol.24,
no.3, Mar.2006.
L. G. Barbero, J. Thompson, "A Fixed-Complexity MIMO
Detector Based on the Complex Sphere Decoder," Inst.
for Dig. Commun., University of Edinburgh, United
Kingdom.
L. G. Barbero, J. Thompson, "Fixing the Complexity of
the Sphere Decoder for MIMO Detection", IEEE
Transactions on Wireless Communicactions, Vol. 7,
No. 6, June 2008.
E. Zimmermann, W. Rave, G. Fettweis, "On the
Complexity of Sphere Decoding," Dresden Univ. of
Tech., Vodafone Chair Mob. Commun. Systems.
A. Chan, I. Lee, "A New Reduced Complexity Sphere
Decoder For Multiple Antenna Systems," IEEE
International Conf. on Commun., New York, USA,
vol. 1, pp. 460-464, Apr. 2002.
N. Noording, B. Ali, S. Jamuar, M. Ismail, "A Simplified
Sphere Decoding Algorithm for MIMO Transmission
System," University Putra, Malaysia.
SIGMAP2012-InternationalConferenceonSignalProcessingandMultimediaApplications
80
