From PID to Extended Learning Control
Cristiano Maria Verrelli
Electronic Engineering Department of ”Tor Vergata” University, Via del Politecnico 1, 00133 Rome, Italy
Keywords:
Learning Control, Uncertain Nonlinear Systems, Minimum Phase, Output Feedback Form, PID Control,
Permanent Magnet Step Motors.
Abstract:
It has been recently shown in Marino, Tomei, and Verrelli (2011) that the output error feedback regulation
problem with (unknown) periodic reference and/or disturbance signals of known common period can be ef-
fectively solved for the class of single-input, single-output, minimum phase, nonlinear, time-invariant systems
in output feedback form (of known relative degree one or two) which are affected by unknown parameters and
unknown output-dependent nonlinearities. The resulting nonlinear control, which relies on advanced learning
control techniques, can be interpreted as a generalization of the classical PID control which solves the problem
when both reference and disturbance signals are constant. In this paper, we present sophisticated analytical
arguments which prove that the learning control designed in Marino, Tomei, and Verrelli (2011) can be en-
dowed with a period identifier when the output reference signal is periodic of uncertain period but available at
each time instant. The generalized resulting control preserves the achievement of the closed loop properties
obtained in Marino, Tomei, and Verrelli (2011) while maintaining an overall simple structure. The application
of the presented control techniques to the position synchronization problem for current-fed permanent magnet
step motors with non-sinusoidal flux distribution and uncertain position-dependent load torque allows us to
provide a solution to a yet unsolved problem.
1 INTRODUCTION
Learning control design relies on the common obser-
vation that human beings are able to improve task exe-
cutions through repeated trials. In contrast to general
non-learning ones, learning controllers suitably use,
in a repetitive framework, the richness of informa-
tion owned by error signals from previous executions
(Ahn, Chen, and Moore (2007), Bristow, Tharayil,
and Alleyne (2006)). Learning controls thus itera-
tively extract from the past the sufficient experience to
improve the closed loop performances and to guaran-
tee the output tracking even for nonlinear systems af-
fected by large uncertainties and disturbances. In par-
ticular, it has been recently shown in Marino, Tomei,
and Verrelli (2011) that for the classes of:
• single-input, single-output, minimum phase, un-
certain, nonlinear, time-invariant n-dimensional
systems in output feedback form
1
1
x ∈ R
n
, u ∈ R, y ∈ R, w ∈ R
n
; ψ(·) is an unknown
smooth vector-valued function; 0
(ρ−1)×1
is the column vec-
tor with (ρ − 1) zero-components.
˙x =






0 1 0 ··· 0
0 0 1 ·· · 0
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
0 0 0 ·· · 1
0 0 0 ·· · 0






x + ψ(y)
+





0
(ρ−1)×1
b
ρ
.
.
.
b
n





u + w (1)
y = [1,0,···,0]x
with known relative degree ρ ∈ {1,2} and
b
ρ
,.. .,b
n
∈ R
+
unknown positive reals such that
the zeroes of the polynomial p(s) = b
ρ
s
n−ρ
+...+
b
n
all belong to C
−
;
• single-input, single-output, observable, minimum
phase, uncertain, linear, time-invariant systems
2
˙
ζ = Fζ + gu + w (2)
y = hζ
with known relative degree ρ ∈ {1, 2} and input-
2
ζ ∈ R
n
, u ∈ R, y ∈ R, w ∈ R
n
; F ∈ M (n,R), g ∈ R
n
,
h
T
∈ R
n
are unknown.
464
Maria Verrelli C..
From PID to Extended Learning Control.
DOI: 10.5220/0004029104640469
In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 464-469
ISBN: 978-989-8565-21-1
Copyright
c
 2012 SCITEPRESS (Science and Technology Publications, Lda.)

output transfer function
3
W (s) =
L(y(t))[s]
L(u(t))[s]
=
b
ρ
s
n−ρ
+ .. . + b
n
s
n
+ a
1
s
n−1
+ .. . + a
n
whose zeroes all belong to C
−
,
the PD-type learning control
4
u(t) = −(ρ − 1)k
D
˙
˜y(t) − k
P
˜y(t) + ˆu
∗
(t)
ˆu
∗
(t) = sat
M
u
( ˆu
∗
(t − T ))−k
I
T ϕ
T
(t)

(ρ − 1)

˙
˜y(t)
+k
P
/k
D
˜y(t)

+ (2 − ρ) ˜y(t)

(3)
ˆu
∗
(t) = 0, ∀ t ≤ 0
˜y(t) = y(t) − y
∗
(t)
is able to guarantee (with a proper choice of the con-
trol gains) the asymptotic output tracking
lim
t→+∞
[y(t) − y
∗
(t)] = 0
of (unknown) periodic output reference signals
y
∗
∈ C
p
y
(p
y
∈ N
≥1+ρ
) of known period T despite
the presence of the (unknown) periodic disturbance
vector signal w ∈ C
p
w
(p
w
∈ N
≥ρ
) of the same period
T .
Control (3) can be interestingly interpreted as a
generalization of the classical PID control
u(t) = −(ρ − 1)k
D
˙
˜y(t) − k
P
˜y(t) − k
I
Z
t
0
˜y(τ)dτ (4)
whose development started about one hundred years
ago (see Sperry (1922) and Minorsky (1922)) and
which, with a proper choice of the control gains, guar-
antees for the above classes of systems asymptotic
output regulation in the case of constant output ref-
erence signals y
∗
and disturbances w. If the classical
PID control is equivalently rewritten as
u(t) = −(ρ − 1)k
D
˙
˜y(t) − k
P
˜y(t) + ˆu
∗
(t)
˙
ˆu
∗
(t) = −k
I
˜y(t), ˆu
∗
(0) = 0,
3
L[ f (t)](s) denotes the Laplace transform of the time
function f (t) : R
+
∪ {0} → R, s ∈ C, b
i
∈ R
+
and a
j
∈ R
are unknown reals, ρ ≤ i ≤ n, 1 ≤ j ≤ n.
4
The reals k
D
, k
P
, k
I
, M
u
are suitable positive control pa-
rameters; sat
M
u
(·) : R → [−M
u
,M
u
] is a continuous odd in-
creasing function satisfying sat
M
u
(q) = q for any q ∈ (0, M
u
]
and sat
M
u
(q) = M
u
for any q > M
u
; ϕ
x
(·) : R
+
∪{0} → [0, 1]
(x > 0) is a continuous increasing function for t ∈ [0,x] with
ϕ
x
(0) = 0 and ϕ
x
(t) = 1 for any t ≥ x.
it can be clearly noticed that k
D
and k
P
in (3) play the
roles of the derivative and proportional gains in (4)
while the learning estimation scheme
ˆu
∗
(t) = sat
M
u
( ˆu
∗
(t − T ))−k
I
T ϕ
T
(t)

(ρ − 1)

˙
˜y(t)
+k
P
/k
D
˜y(t)

+ (2 − ρ) ˜y(t)

(5)
ˆu
∗
(t) = 0, ∀ t ≤ 0
apparently extends the integral action −k
I
R
t
0
˜y(τ) to
the case of periodic references/disturbances. By ne-
glecting the saturation action and by taking the limit
for T → 0 (if it exists), we can in fact obtain
ˆu
∗
(t) = −k
I
Z
t
0

(ρ − 1)

˙
˜y(τ) + k
P
/k
D
˜y(τ)

+(2 − ρ) ˜y(τ)

dτ
.
= ˆu
∗
(0) − k
I
(ρ − 1) ˜y(t) (6)
−k
I
Z
t
0

(ρ − 1)k
P
k
D
˜y(τ) + (2 − ρ) ˜y(τ)

dτ.
The signal ˆu
∗
, in both the above controls, plays
the role of estimating the unknown reference input
u
∗
which guarantees perfect output tracking for
compatible initial conditions with u
∗
being restricted
to be periodic of period T for (3) or simply constant
(periodic of any period T ) for the classical PID
control.
2 THE CASE OF THE
UNCERTAIN PERIOD
Control (3) feeds back only the regulation error ˜y(t)
(and its time derivative
˙
˜y(t) if ρ = 2). However it
relies on the knowledge of the period T characteriz-
ing the periodic reference signal y
∗
(t) and disturbance
vector signal w(t). The aim of this section is to pro-
vide a generalization of the learning control presented
in Marino, Tomei, and Verrelli (2011) to the case in
which the output reference signal y
∗
(t) is periodic of
uncertain period T but measurable at each time instant
t.
2.1 Control Design
Assume that the uncertain period T belongs to a cer-
tain compact set and that a known upper bound T
M
on
T is available (T ≤ T
M
) along with a nominal value
FromPIDtoExtendedLearningControl
465

T
N
≤ T
M
of T which is not necessarily equal to it. By
setting T
N
in place of the uncertain T in (3), we obtain
[µ = k
I
T
N
]
u(t) = −(ρ − 1)k
D
˙
˜y(t) − k
P
˜y(t) + ˆu
∗
(t)
ˆu
∗
(t) = sat
M
u
( ˆu
∗
(t − T
N
)) − µϕ
T
N
(t)

(ρ − 1)

˙
˜y(t)
+k
P
/k
D
˜y(t)

+ (2 − ρ) ˜y(t)

(7)
ˆu
∗
(t) = 0, ∀ t ≤ 0.
If T
N
6= T , then asymptotic output regulation
lim
t→+∞
[y(t) − y
∗
(t)] = 0
my be in general not achieved. With the aim of incor-
porating a suitable period identifier, we first rewrite
the input reference as u
∗
(t) = u
∗α
(t) + u
∗β
(t) where:
• u
∗α
(t) and u
∗β
(t) are periodic time functions of
period T
N
and T , respectively;
• each u
∗ j
(·), j = α,β, is restricted to be either u
∗
(·)
or the identically null function N (·) ≡ 0.
If T
N
= T then, without loss of generality, u
∗α
(·) =
u
∗
(·) and u
∗β
(·) = N (·); if T
N
6= T then u
∗β
(·) = u
∗
(·)
and u
∗α
(·) = N (·). In any case, both u
∗ j
(·), j = α, β,
satisfy |u
∗ j
(t)| ≤ M
u
. We then modify (7) as (µ and ν
are the new positive learning gains)
u(t) = −(ρ − 1)k
D
˙
˜y(t) − k
P
˜y(t) + ˆu
∗α
(t) + ˆu
∗β
(t)
ˆu
∗α
(t) = sat
M
u
( ˆu
∗α
(t − T
N
)) − µϕ
T
N
(t)

(ρ − 1)

˙
˜y(t)
+k
P
/k
D
˜y(t)

+ (2 − ρ) ˜y(t)

ˆu
∗α
(t) = 0, ∀ t ≤ 0
ˆu
∗β
(t) = sat
M
u
( ˆu
∗β
(t −
ˆ
T (t))) − νϕ
T
M
(t)

(ρ − 1)

˙
˜y(t)
+k
P
/k
D
˜y(t)

+ (2 − ρ) ˜y(t)

ˆu
∗β
(t) = 0, ∀ t ≤ 0
where ˆu
∗ j
(·), j = α,β, play the role of estimating the
unknown periodic functions u
∗ j
(·), j = α,β. Accord-
ing to the recent advances in Verrelli (2011a), the esti-
mate of the uncertain period T results from an explo-
rative search in the domain of the admissible values
for T (see also Tyukin (2011) for similar explorative
approaches). We accordingly introduce the estimate
ˆ
T of the uncertain period T defined as
ˆ
T (t) = T
M
(8)
for 0 ≤ t < 2T
M
and satisfying [M ∈ N ∪ {+∞}]
˙
ˆ
T (t) =

0 if
∑
M
i=0
|y
∗
(π
i
) − y
∗
(π
i
+
ˆ
T (t))| = 0
−1 otherwise,
(9)
for t ≥ 2T
M
. If the set Σ = {π
i
,0 ≤ i ≤ M} is chosen
as the (countable) set of all rational numbers in [0,T
M
]
with the field Q being a dense subset of R, then
ˆ
T
belongs to the compact set [T,T
M
] and converges
to the uncertain T in finite time 3T
M
− T . In fact,
by contradiction, suppose that
ˆ
T (3T
M
− p) = p
satisfying
∑
M
i=0
|y
∗
(π
i
) − y
∗
(π
i
+ p)| = 0 is different
from T or equivalently that there exists a certain
ϖ ∈ R / Q∩ [0,T
M
] such that |y
∗
(ϖ)−y
∗
(ϖ+ p)| 6= 0;
then, since y
∗
(t) is a continuous function, there will
exist a neighbourhood ϒ ⊂ R of ϖ such that
|y
∗
(t) − y
∗
(t + p)| 6= 0 for any t ∈ ϒ, with ϒ contain-
ing at least one element of Q ∩ [0,T
M
].
Remark 1: The estimate
ˆ
T may converge in finite time
to T via a finite number M of evaluations when y
∗
is a
band-limited periodic signal with zero spectrum out-
side the compact set [−ω
y
/2,ω
y
/2] with T
m
a positive
lower bound on T. In this case, it suffices:
• to set, according to the sampling theorem 6.4
in Kalouptsidis (1997), π
i
= iT
M
/M
.
= iT
s
, i =
0,2,. .., M with T
s
≤ 2π/ω
y
provided that T lies
on the sequence of π
i
;
• to design Σ such that card (Σ ∩ [0, T
m
]) > 2
¯
M with
¯
M denoting the order of the trigonometric polyno-
mial y
∗
(t) =
∑
¯
M
k=−
¯
M
c
k
e
ik2πt/T
.
2.2 Mathematical Details
Instead of using the Lyapunov function in Marino,
Tomei, and Verrelli (2011) V (t) = W (t) + T (t) with
T (t) = (2µ)
−1
Z
t
t−T
[u
∗
(τ) − sat
M
u
( ˆu
∗
(τ))]
2
dτ
consider the function
V (t) = W (t) + (2µ)
−1
Z
t
t−T
N
[u
∗α
(τ) − sat
M
u
( ˆu
∗α
(τ))]
2
dτ
+(2ν)
−1
Z
t
t−
ˆ
T
∗
(t)

u
∗β
(τ) − sat
M
u

ˆu
∗β
(τ)

2
dτ
in which
ˆ
T
∗
(t) is a suitable class C
1
cubic spline-
based approximation of
ˆ
T (t) (with non-negative
˙
ˆ
T
∗
(t)) which differs from
ˆ
T (t) only on an arbitrarily
small compact set. The same closed loop convergence
properties established in Marino, Tomei, and Verrelli
(2011), that is:
• x(t) and u(t) are bounded on [0,+∞);
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
466

• ˜y(t) - and
˙
˜y(t) if ρ = 2 - asymptotically tend to
zero as t → +∞ and are exponentially attracted
into residual connected compact sets containing
the origin whose diameters decrease as the learn-
ing gains increase;
• the asymptotic input learning
lim
t→+∞
[u(t) − u
∗
(t)] = 0
is achieved under certain mild condition involving
the speed of convergence of the output tracking
errors ˜y (and
˙
˜y if ρ = 2),
are obtained by recognizing, in the computation of
˙
V ,
the following crucial facts:
•
˙
ˆ
T
∗
multiplies, in
˙
V , the non-negative term
L(t) =
1
2ν
[u
∗β
(t −
ˆ
T
∗
(t)) − sat
M
u
( ˆu
∗β
(t −
ˆ
T
∗
(t)))]
2
;
• u
∗β
(t −
ˆ
T
∗
(t)) − u
∗β
(t − T ) = 0 if T = T
N
(i.e. if
u
∗β
(·) = N (·));
• |u
∗β
(t −
ˆ
T
∗
(t))−u
∗β
(t −T )| ≤ c
u
|T −
ˆ
T
∗
(t)| if T 6=
T
N
(i.e. if u
∗α
(·) = N (·)) with c
u
being a bound
on | ˙u
∗
(t)|;
•
ˆ
T belongs to the compact set [T,T
M
] and con-
verges in finite time to T .
3 SIMULATION RESULTS
We apply the control techniques proposed in the pre-
vious section to solve the tracking control problem ad-
dressed in Bifaretti, Tomei, and Verrelli (2011) (see
also Bifaretti, Iacovone, Rocchi, Tomei, and Ver-
relli (2011) for experimental results) for uncertain
current-fed permanent magnet step motors with non-
sinusoidal flux distribution and uncertain position-
dependent load torque. In constrast to Bifaretti,
Tomei, and Verrelli (2011), a reference signal for the
rotor position [θ
∗
(t) =
3
π
[1 − cos(π/3t)] rad in Figure
1] - periodic of uncertain period T = 6 s and available
at each time instant t (along with
˙
θ
∗
(t)) - is required
to be tracked in this case. In other terms, a master-
slave synchronization problem (see Verrelli (2011a)
and Verrelli (2012)) is considered, in which the mea-
sured position θ
∗
(t) - periodic of uncertain period - of
the master drumming human arm constitutes the ref-
erence signal to be tracked by the position θ(t) of the
slave drumming robotic arm connected to the PMSM
motor(see Figure 2): the periodic human arm move-
ment is to be imitated by the robotic arm one (Andry,
Gaussier, Moga, Banquet, and Nadel (2001)). The
problem of synchronizing robots with external sig-
nals has been largely studied in the field of humanoid
robotics. Musical performances - drumming in par-
ticular - in fact exemplifies the kind of synchroniza-
tion challenge in which humans excel and at which
robots typically fail. The results of this section, in the
case of current-fed motor operations, will extend the
ones presented in Verrelli (2011a) to the case of un-
certainties in all motor parameters excepting N
r
(re-
call that the model for the surface-mounted perma-
nent magnet synchronous motor in Verrelli (2011a)
is a particular case of the model considered in this
section). On the other hand, current-fed motor opera-
tions are related to the use of high gains in the current
loop which the presence of severe model uncertain-
ties lead to (see Marino, Tomei, and Verrelli (2012)
and Verrelli (2011b)). The learning control algorithm
proposed in Bifaretti, Tomei, and Verrelli (2011) is a
slight modification of the generalized PID control (3)
with ρ = 2. It si designed for the current-fed perma-
nent magnet step motor with two phases in the (d,q)
reference frame rotating at speed N
r
ω and identified
by the angle N
r
θ in the fixed (a, b) reference frame
attached to the stator [θ is the rotor position, ω is the
rotor speed and N
r
is the number of rotor teeth, m ≥ 4
is an uncertain integer]
dθ(t)
dt
= ω(t)
dω(t)
dt
= −
D
J
ω(t) + 2N
r
L
1
i
d
(t)i
q
(t)
+
i
f
N
r
J
m
∑
j=1
jL
m j
cos[(1 − j)N
r
θ(t)]i
q
(t)
+
i
f
N
r
J
m
∑
j=2
jL
m j
sin[(1 − j)N
r
θ(t)]i
d
(t)
−
N
r
i
2
f
2J
m
∑
j=4
jL
f j
sin[ jN
r
θ(t)] −
T
L
(θ(t))
J
where: (i
d
,i
q
) are the stator current vector (d,q)
components [which constitute the control inputs],
D is the friction coefficient, J is the rotor inertia,
T
L
(·) is the load torque, i
f
is the fictitious con-
stant rotor current provided by the permanent mag-
net, L
1
is a non-negative parameter, the harmon-
ics
∑
m
j=1
L
m j
cos[ jN
r
θ] and
∑
m
j=1
L
m j
cos

jN
r
θ −
π
2

model the non-sinusoidal flux distribution in the air-
gap with the parameters L
m j
, 2 ≤ j ≤ m (which
are zero under the standard assumption of sinusoidal
flux distribution) being much smaller than L
m1
, the
term
N
r
i
2
f
2
∑
m
j=4
jL
f j
sin[ jN
r
θ] represents the distur-
bance torque due to cogging.
The simulation is carried out with reference to
the permanent magnet step motor in Bifaretti, Tomei,
FromPIDtoExtendedLearningControl
467

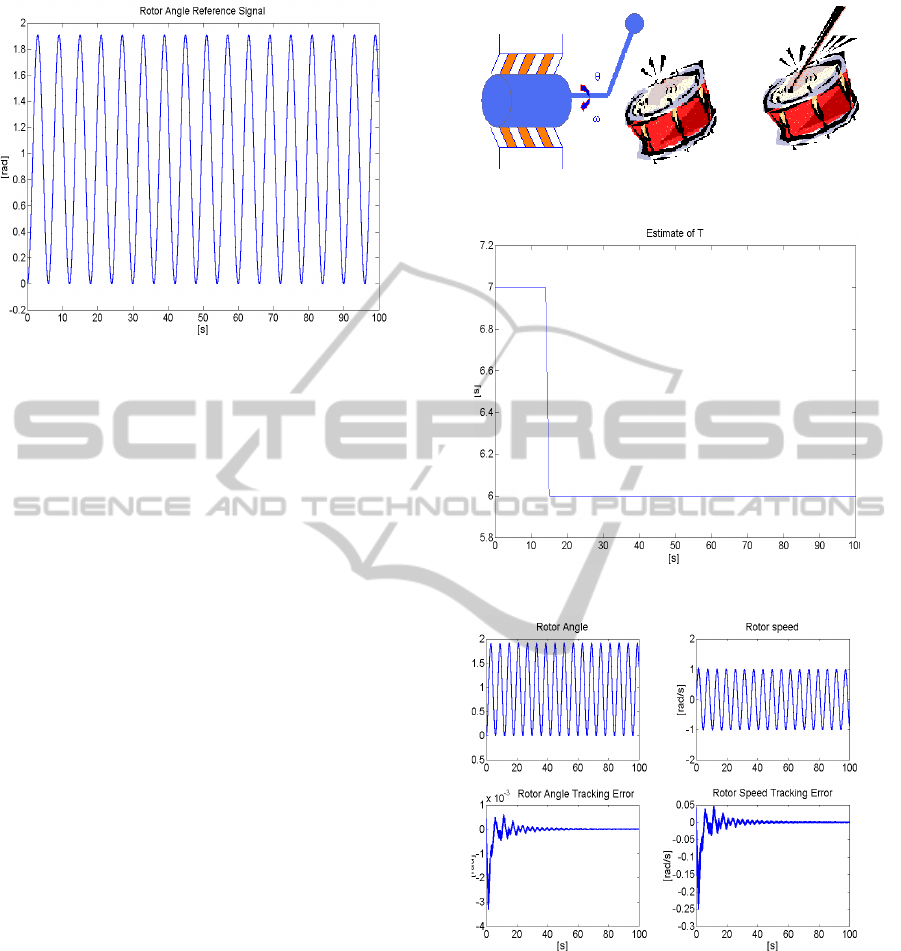
Figure 1: Rotor angle reference signal θ
∗
(t).
and Verrelli (2011) and Krishnamurthy and Khorrami
(2003) with load torque T
L
(θ) = N
T
sin(θ) and pa-
rameters: J = 0.0733 Kgm
2
, L
1
= 0, m = 4, L
m1
= 5
mH, L
m2
= 0.5 mH, L
m3
= 0.166 mH, L
m4
= 0.0625
mH, L
f 4
= 1.766 mH, N
r
= 50, i
f
= 1 A, D = 0.002
kgm
2
/s, N
T
= 1.7201 kgm
2
/s
2
. The considered appli-
cation is the robotic application described in Dawson,
Hu, and Burg (1998) (see Figure 2) in which the load
torque T
L
= N
T
sin(θ) models the position-dependent
single link robotic load represented by a metal bar link
attached to the rotor shaft and a brass ball attached to
the free end. All the motor initial conditions are set
to zero as in a realistic setting in which the motor is
initially at rest and the initial position is compatible
with the corresponding reference signal. According
to Section 2, the learning control algorithm reads
i
d
(t) ≡ 0
i
q
(t) = −k
ω
˜
ω(t) − k
v
˜
θ(t) + ˆu
∗α
(t) + ˆu
∗β
(t)
ˆu
∗α
(t) = sat
M
u
( ˆu
∗α
(t − T
N
)) − µϕ
T
N
(t)
˜
ω(t)
ˆu
∗α
(t) = 0, ∀ t ≤ 0
ˆu
∗β
(t) = sat
M
u
( ˆu
∗β
(t −
ˆ
T (t))) − νϕ
T
M
(t)
˜
ω(t)
ˆu
∗β
(t) = 0, ∀ t ≤ 0
˜
θ(t) = θ(t) − θ
∗
(t)
˜
ω(t) = ω(t) + k
θ
˜
θ(t) −
˙
θ
∗
(t)
with
ˆ
T (t) given by (8)-(9) and control parameters (all
values are in SI units) k
θ
= µ = ν = 72, k
ω
= 12, k
v
=
1, T
N
= 3.5 s, T
m
= 2 s, T
M
= 7 s and ϕ
x
(t) = t
2
/x
2
for
t ∈ [0, x]. The choice: π
i
= 0.6 +0.6(i −1), 1 ≤ i ≤ 4
guarantees, according to Remark 1, the convergence
of
ˆ
T (t) to T = 6 s in 1 s (see Figure 3). Figure 4
shows the time histories of the rotor angle θ(t), the ro-
tor speed ω(t) and the rotor angle and speed tracking
errors
˜
θ(t),
˜
ω(t), while Figure 5 shows the time his-
tories of the uncertain function u
∗
(t) with its estimate
Figure 2: Slave PMSM motor and master drummer.
Figure 3: Estimate
ˆ
T (t).
Figure 4: Rotor angle θ(t), rotor speed ω(t) and rotor angle
and speed tracking errors
˜
θ(t),
˜
ω(t).
ˆu
∗
(t) = ˆu
∗α
(t)+ ˆu
∗β
(t). Satisfactory position tracking
is achieved despite system uncertainties along with
satisfactory estimation of the uncertain periodic input
reference signal u
∗
(t).
4 CONCLUSIONS
The mathematical details concerning a generalization
ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics
468

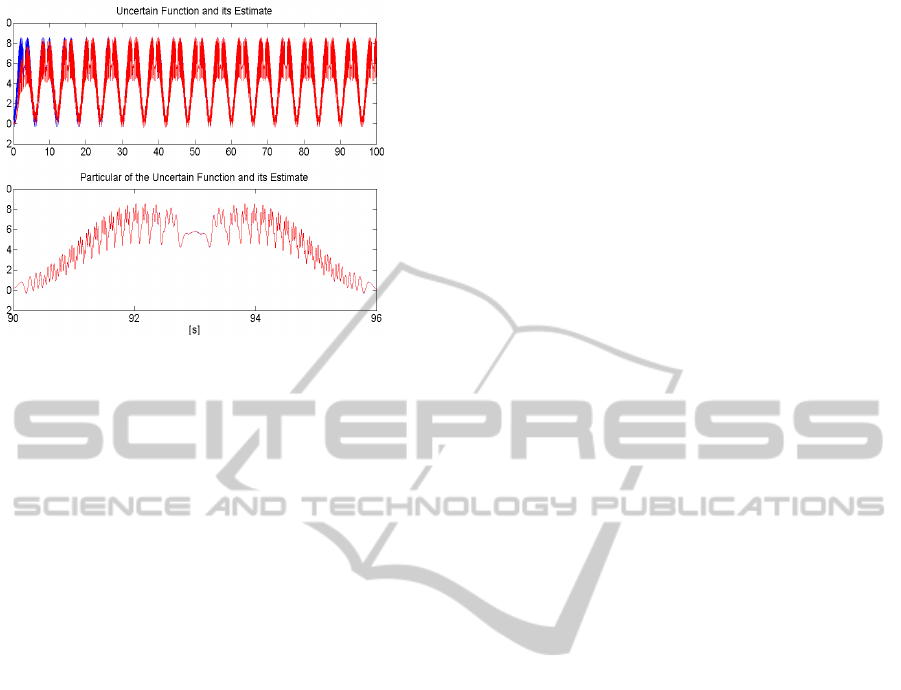
Figure 5: Reference input u
∗
(t) and its estimate ˆu
∗
(t).
of the learning control design presented in Marino,
Tomei, and Verrelli (2011) are provided. The derived
solution is able to solve the output regulation problem
when the output reference signal (available at each
time instant) is periodic of uncertain period. Sophis-
ticated analytical arguments show that the resulting
learning control, which incorporates the generalized
PID learning control of Marino, Tomei, and Verrelli
(2011) as a special case, preserves the achievement of
the closed loop properties obtained in Marino, Tomei,
and Verrelli (2011). The effectiveness of the result
presented in the paper is demonstrated by its success-
ful application to the yet unsolved position synchro-
nization problem for current-fed permanent magnet
step motors with non-sinusoidal flux distribution and
uncertain position-dependent load torque.
REFERENCES
H.-S. Ahn, Y. Chen, and K. L. Moore (2007). Itera-
tive learning control: brief survey and categorization.
IEEE Transactions on Systems, Man, and Cybernet-
ics, C, 37, 1099-1121.
P. Andry, P. Gaussier, S. Moga, J. P. Banquet, and J. Nadel
(2001). Learning and communication via imitation:
an autonomous robot perspective. IEEE Transactions
on Systems, Man, and Cybernetics - Part A: Systems
and Humans 31, 431-442.
S. Bifaretti, V. Iacovone, A. Rocchi, P. Tomei, and C. M.
Verrelli (2011). Global learning position controls for
permanent magnet step motors. IEEE Transactions on
Industrial Electronics, 58, 4654-4663.
S. Bifaretti, P. Tomei, and C. M. Verrelli (2011). A global
robust iterative learning position control for current-
fed permanent magnet step motors. Automatica, 47,
227-234.
D. A. Bristow, M. Tharayil, and A. G. Alleyne (2006). A
survey of iterative learning control. IEEE Control Sys-
tems Magazine, 96-114.
D. M. Dawson, J. Hu, and T. C. Burg (1998). Nonlinear
Control of Electric Machinery, Marcel Dekker.
N. Kalouptsidis (1997). Signal Processing Systems, John
Wiley & Sons.
P. Krishnamurthy and F. Khorrami (2003). Robust adap-
tive voltage-fed permanent magnet step motor control
without current measurements. IEEE Transactions on
Control Systems Technology, 11, 415-425.
R. Marino, P. Tomei, and C. M. Verrelli (2012). Robust
adaptive learning control for nonlinear systems with
extended matching unstructured uncertainties. Inter-
national Journal of Robust and Nonlinear Control, 22,
645-675.
R. Marino, P. Tomei, and C. M. Verrelli (2011). Generalized
PID learning control. 18
th
IFAC World Congress, 18,
28 August-2 September.
N. Minorsky (1922). Directional stability of automatically
steered bodies. American Society of Naval Engineers.
E. Sperry (1922). Automatic steering. Transactions of
ASME.
I. Tyukin (2011). Adaptation in Dynamical Systems, Cam-
bridge University Press.
C. M. Verrelli (2011a). Fourier series expansion for syn-
chronization of permanent magnet electric motors.
Applied Mathematics and Computation, 217, 4502-
4515.
C. M. Verrelli (2012). Synchronization of permanent mag-
net electric motors: new nonlinear advanced results.
Nonlinear Analysis: Real World Applications, 13,
395-409.
C. M. Verrelli (2011b). Adaptive learning control for
robotic manipulators driven by permanent magnet
synchronous motors. International Journal of Con-
trol, 84, 1024-1030.
FromPIDtoExtendedLearningControl
469