Adaptive Data Update Management in Sensor Networks

C. M. Krishna

ECE Department, University of Massachusetts at Amherst, Amherst, U.S.A.

Keywords:

Sensor Networks, Energy-aware Computing, Energy Harvesting, Accuracy Balancing.

Abstract:

Transmitting messages is by far the most energy-intensive thing that most sensors do. We consider the problem

of a sensor which regularly senses some parameter in its operating environment. Based on the value it knows

to have been estimated at the base station (or other central information collation station) for that parameter,

the actual sensed value, its remaining energy levels, and other quantities such as the time-to-go in the mission

(if limited) or the anticipated energy inﬂow (if energy harvesting is used), it decides whether that sensed value

is worth transmitting. We present heuristics to make this decision and evaluate their performance.

1 INTRODUCTION

We address the following problem. We have a sin-

gle sensor, which samples the value of some environ-

mental parameter at periodic intervals. It then has to

decide whether or not it is worth the expense of trans-

mitting this information. We explore heuristics for

doing so in two cases: Case 1: There is a ﬁxed over-

all energy store, and Case 2: The network harvests

energy from the operating environment.

The problem arises from the fact that broadcasting

is by far the most energy-expensive thing that most

sensor nodes can do. By comparison with the energy

it takes to send a message, the act of sensing, i.e., of

obtaining the information to be transmitted, takes al-

most negligible energy in most instances, especially

since the node can sleep between sampling epochs.

The decision as to whether or not to transmit is

based on the following considerations: (a) The value

of the sensed parameter, (b) the value that would be

estimated by the user if this parameter were to be sup-

pressed at the sensor rather than being reported to the

user, (c) the current energy state at the sensor, and (d)

the residual mission lifetime (if this is limited). If en-

ergy reserves are replenished by harvesting from the

operating environment, an additional factor is the an-

ticipated near-term inﬂows of energy from such har-

vesting.

Our contributions in this paper are to develop

lightweight adaptive algorithms to decide whether

or not to transmit for the two cases. Our adaptive

thresholding algorithms do not require any informa-

tion about the operating environment. Rather than

keep the sensor value within some speciﬁed bounds,

their aim is to provide some means to do “accuracy

balancing” over time, i.e., keep the minimum accu-

racy of the information at the base station at roughly

the same level over the period of operation. Such an

approach would be useful when the priority is to keep

the network functioning over a given period under the

assumption that the deleterious impact of inaccuracy

is the same at any point in time. It would be useful

when the cost of inaccuracy is a roughly linear func-

tion of the inaccuracy with which the sensor informa-

tion is known.

Our MDT-based algorithm imposes a greater com-

putational load, but that problem can be circumvented

by carrying out most of these calculations ofﬂine and

storing the appropriate action in a lookup table.

2 RELATED PRIOR WORK

2.1 Adaptive Data Aggregation and

Reporting

A number of authors have reported work on adaptive

data aggregation and reporting in sensor networks.

We list here a representative sample of them.

One of the ﬁrst contributions in this area was

the approach of Goel and Imielinski (2001). They

borrowed from the compression techniques used for

MPEG video. The ﬁeld of data generated from spa-

tially distributed sensors can be visualized as inten-

sity values in an image. Existing MPEG spatial and

temporal compression techniques can then be used to

exploit the spatio-temporal correlation that exists be-

tween neigbouring sensor values.

Deshpande, et al. (2004) follow the idea of learn-

476

M. Krishna C..

Adaptive Data Update Management in Sensor Networks.

DOI: 10.5220/0004034404760481

In Proceedings of the 9th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2012), pages 476-481

ISBN: 978-989-8565-21-1

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

ing the spatial and temporal correlations of sensor

data. Santini and Romer (2006) use a Least-Mean-

Square (LMS) adaptive algorithm for making predic-

tions given a data stream. Han, et al. (2007) consider

sensor transmissions that are either source-triggered

or consumer-triggered (the consumers are the queries

that come into the system, asking for parameter infor-

mation). In all these cases, the sensor transmission is

suppressed if it would not add sufﬁcient value.

Ahmadi and Abdelzaher (2009) take reliability

into consideration. In particular, they take into ac-

count the fact that wireless networks are often noisy

and drop packets.

2.2 Energy Harvesting

Energy harvesting has been the focus of increasing

interest. Surveys of energy harvesting techniques can

be found in Chalasani and Conrad (2008) and Park,

et al. (2007). Related power management techniques

are studied in Kansal, et al. (2007) and Sharma, et

al. (2010). These include migrating tasks to nodes

depending on their energy levels. Task scheduling in

energy harvesting real-time systems is considered in

Moser, et al. (2007); their algorithms take into ac-

count both the prevailing energy and time constraints,

rather than simply the task timing constraints.

3 MODELS

3.1 Environmental Model

The sensed environment has a behaviour as projected

by the user. For example, if we have a sensor mea-

suring outdoor temperature, there could be a formula

that uses the current time-of-day and the last few re-

ported observations to estimate the current tempera-

ture at the sensor. Since there are stochastic aspects

to the sensed environment (if the environment were

not stochastic there would be no need to use a sen-

sor), the actual parameter value can vary from that es-

timated. The amount of variation from the estimated

value obviously depends on the age of the information

that is used to make the estimate: the temperature at

10:05 AM is likely to be estimated very accurately if

the temperature at 10:00 AM was reported; by con-

trast, if the last temperature report was at 8:00 AM,

the estimate is likely to be of poorer accuracy.

In our environmental model, we do not model the

actual value of the sensed variable. Instead, we model

the difference, δ, between the actual value and the

projected value. It is in this difference that all the

stochastic nature of the environment is captured. For

example, if the sensed variable is treated as falling

in some set of discrete quantities (which is the case

in ﬁnite word-length machines even if the underlying

sensed variable is continuous), we use the probability

mass function (pmf), π

(∆), of the additional devia-

tion, ∆, of the actual, from the projected (or modelled)

value, arising from the passage of one sampling pe-

riod. That is, if the state variable was last reported at

sampling point n, the divergence from the projected

value would be ∆

+···+∆

at sampling point n+m,

where the ∆

follow the pmf π

(·).

It is important to recognise that our algorithm does

not require a prior model of the environment to be

available. If one such is available, it can be used to

project into the future, the value of the next parameter

sample. A simple case would be where, for instance,

the ∆

can be modeled as i.i.d. random variables. For

example, in our numerical examples, we assume for

concreteness that π

(·) is a geometrically distributed

random variable truncated at some maximum devia-

tion: π

(i) = Kα

|i|

if −D

max

≤ i ≤ D

max

and 0 oth-

erwise, where α is a constant characterizing the ran-

dom process, K is a normalization constant and D

max

is some given truncation point.

However, if such a prior model is not available, we

can simply use some extrapolation techniques based

on recent observationsto project what the next sample

value will be.

Regardless of whether we use an environmental

model, extrapolation, or a combination of the two, the

sensor is able to replicate, without communication,

the value that the base station would project (based

on its prior transmissions) in the absence of a report

of its current value. In other words, the sensor can

calculate what the base station would estimate for the

current value of the parameter based on the prior sen-

sor reports. Since it has the actual measured value of

the current parameter value, it knows the divergence

between these two quantities.

3.2 Cost Measure

Our cost measure is the sum of the absolute errors as

a result of not reporting the value of every sample that

is measured. That is, let B

be the broadcast indicator

function,



1 if sampling point i is reported

0 otherwise

Deﬁne L

as the last sampling point prior to i whose

value was reported. Then, the aggregate cost incurred

up to (and including) some sampling point i is given

Θ(i) =

∑

j=1

(1− B

)

−1

∑

k=1

|∆

AdaptiveDataUpdateManagementinSensorNetworks

477

where the ∆

are, as speciﬁed before.

This cost measure allows us to carry out approxi-

mate accuracy balancing. That is, for a given amount

of available energy, we try to ensure that the accu-

racy of the best value at the sink node (base station) is

roughly balanced over the lifetime of the system.

Our algorithms are by no means limited to this

cost measure. They can, in fact, take any other cost

function that may be more appropriate to the applica-

tion.

4 FIXED ENERGY BUDGET AND

FINITE MISSION LIFETIME

We start by considering the problem of a ﬁxed en-

ergy budget (provided, for example, by a battery) and

a speciﬁed ﬁnite mission lifetime. Generally, sens-

ing consumes very little energy and so the number

of broadcasts that the sensor still has energy for ade-

quately characterizing the amount of energy available.

(It is not difﬁcult to relax this assumption by slightly

inﬂating the energy required for transmission; we in-

clude it because it simpliﬁes our description). We will

therefore deﬁne the energy state at any moment as the

number of broadcasts the node is still able to make.

We will assume a simple energy model in which

battery leakage and fading are considered negligi-

ble. Also, we assume that the time between sampling

points is sufﬁcient for the battery to recover from the

(heavy) power draw associated with transmission. If

this is not the case, one can use battery models to

capture this effect: in prior work, Krishna (2011) has

shown how this can be done.

The baseline algorithm against which to compare

our lightweight heuristics is to space the reporting in-

stances as evenly as possible. More concretely, sup-

pose the operating lifetime consists of N sampling

points and we have enough energy only for r trans-

missions. If N = ℓr+ρ for some integer 0 ≤ ρ < r, we

have r− ρ instances where we report every ℓ samples

and ρ instances where we report every ℓ + 1 samples.

4.1 Known Parameter Statistics

When the statistics of the parameter being sensed

are known, we can analytically obtain an appropri-

ate thresholding scheme. If the estimated value ac-

cording to this model diverges from the actual value

(as sensed) by more a speciﬁed threshold, the sensor

transmits. Suppose the interval between successive

samples is τ and the target lifetime of the network is

T. Denote the threshold by θ and, as before, r as the

number of transmissions for which we have energy.

To ensure accuracy balancing, we use our knowledge

of the parameter statistics to set θ so that the average

inter-transmission duration is approximately T/r.

Example: Suppose our knowledge of the sensed pa-

rameter is such that the error (between the estimated

and the last reported measurement) can be modeled

as a Wiener process with zero drift and variance σ

We obtain θ as follows. Consider a Weiner pro-

cess, whose initial value is 0. This represents the

divergence from the sensed value at the last time a

sample was taken and transmitted. Set up absorbing

boundaries for this random walk at θ and −θ. Cal-

culate the expected ﬁrst passage time from the ini-

tial state to one of the boundaries. This is given by

E[t

firstPassage

] = θ

−2

((Domine 1995)). Now, se-

lect θ so that the E[t

firstPassage

] = T/r. This yields

θ = σ

T/r.

In general, let g

(∆

,∆

,·· · ,∆

) be the joint density

function of the deviations of the parameter measured

τ,2τ,·· · ,nτ seconds after the previous measurement.

Denote the time between successive transmissions by

. Deﬁne S

= ∆

+ ··· + ∆

. Then, from our knowl-

edge of the system statistics, we can calculate the fol-

lowing terms:

Prob(t

> τ) = Prob(S

< θ)

Prob(t

> 2τ) = Prob(S

< θ;S

< θ)

Prob(t

> nτ) = Prob(S

< θ;··· ;S

< θ)

The mean time between transmissions is given by

ξ = τ

∑

∞

n=1

P(t

> nτ). Now, set ξ = T/r and solve

(either numerically or analytically depending on the

complexity of the expressions) this equation for θ.

4.2 Unknown Parameter Statistics

When the behaviour of the parameter being sensed is

not known, we can proceed in one of two ways. First,

we can start with some default setting of the thresh-

old and use Bayesian or other methods to learn the

dynamics of the parameter being sensed. This does,

however, impose an overhead on the system, of cal-

culating and maintaining posterior distributions rep-

resenting current knowledge. In this section, we look

at a much simpler method that bypasses the need to

measure parameter dynamics.

In particular, we now present and evaluate a sim-

ple adaptive thresholding heuristic. As mentioned be-

fore, the sensor can assess the current value as es-

timated by the base station, in the absence of this

current transmission. If the current error, deﬁned as

the absolute deviation of the actual current value (as

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

478

known to the sensor) from this estimated value at the

base station is not less than the threshold, the node

transmits. The threshold is adaptively increased or

decreased depending on the ratio of the number of

transmissions that are still possible to the number of

sampling epochs to go to the end of the mission. The

pseudocode is provided in Figure 1.

actual ratio=no of trans still possible/no of sampling epochs left

target ratio= no of trans initially possible/total no of sampling epochs

if (actual ratio

≥

adaptive threshold=1

else if (actual ratio

target ratio)

adaptive threshold++;

else if (actual ratio

target ratio)

adaptive threshold--;

if (current error

≥

adaptive threshold)

transmit

Figure 1: Pseudocode for Adaptive Thresholding Heuristic.

4.2.1 Simulation Results

As mentioned earlier, in our simulations for this pa-

per, we assume (unless stated otherwise) that the de-

viation from the projected value is geometrically dis-

tributed, i.e., the pmf of the deviations is given by

(i) =



Kα

|i|

if − D

max

≤ i ≤ D

max

0 otherwise

Figure 2 provides some performance results. The

Starting Energy Ratio (SER) is the ratio of transmis-

sions that are possible to the number of sampling

epochs. For low SER, the adaptive thresholding al-

gorithm offers no meaningful savings over the base-

line algorithm; indeed, for some extremely low val-

ues, it may actually perform a little worse. The rea-

son is that it takes a few adjustments for the thresh-

old to settle down to an appropriate value; if no more

than a handful of transmissions is possible, the system

may spend most of them while the threshold is still

adjusting signiﬁcantly. For other regions, the adap-

tive thresholding algorithm signiﬁcantly outperforms

the baseline until SER approaches 1. At this point,

we have so much energy that the baseline performs

very well; the adaptive thresholding algorithm now

performs worse than the baseline because it was ini-

tially much too parsimonious while still in its initial

phase of adjusting for the correct threshold. In other

words, when SER is very low, the heuristic loses out

(in relative terms) because it was initially too prof-

ligate with transmissions; when SER approaches 1,

because it was initially too stingy. This can obviously

be dealt with by setting the initial value of the thresh-

old based on our knowledge of how much energy is

D =3

max

Adaptive to Baseline Cost Ratio

Starting Energy Ratio

0.6

0.8

1.2

1.4

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

α=1/5

α=1/4

α=1/3

α=1/2

α=1

0.2

0.4

(a) Heuristic Performance wrt Baseline

max

D =3

Starting Energy Ratio

Expected Total Baseline Cost

α=1/4

600

800

1000

1200

1400

1600

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

α=1/5

200

α=1

α=1/2

α=1/3

400

(b) Performance of Baseline

max

Max Per−Step Abs. Deviation

Adaptive to Baseline Energy Ratio

Starting Energy Ratio

0.2

0.4

0.6

0.8

1.2

1.4

0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

max

Total number of Sampling Epochs = 500; initial threshold = 5

Figure 2: Heuristic Performance: Impact of α.

available. However, note that this is the effect of what

is essentially a startup transient; its relative effect on

the overall performance will therefore dwindle as the

system lifetime goes up.

For smaller values of α, the chances are higher

that the deviation will be small. Figures 2(a) and

(b) show the deterioration that happens with increas-

ing α. When α = 1, the the variation is uniformly

distributed from −D

max

to D

max

. Note that when

SER = 1, the baseline algorithm has enough energy

to transmit each sample, so that the base station has

all the samples and therefore zero cost.

Figure 2c shows the impact of the deviation am-

plitude, D

max

, in each sampling epoch. As might

be expected, when D

max

is just 1, there is not much

variation and the heuristic performs quite well. As

max

increases, the variation per step increases, and

the heuristic deteriorates slightly. However, beyond

max

= 2, the relative performance of the heuristic is

insensitive to the value of D

max

. Henceforth, unless

otherwise stated, all numerical results are provided

for D

max

= 3.

Figure 3 shows the way in which the threshold

AdaptiveDataUpdateManagementinSensorNetworks

479

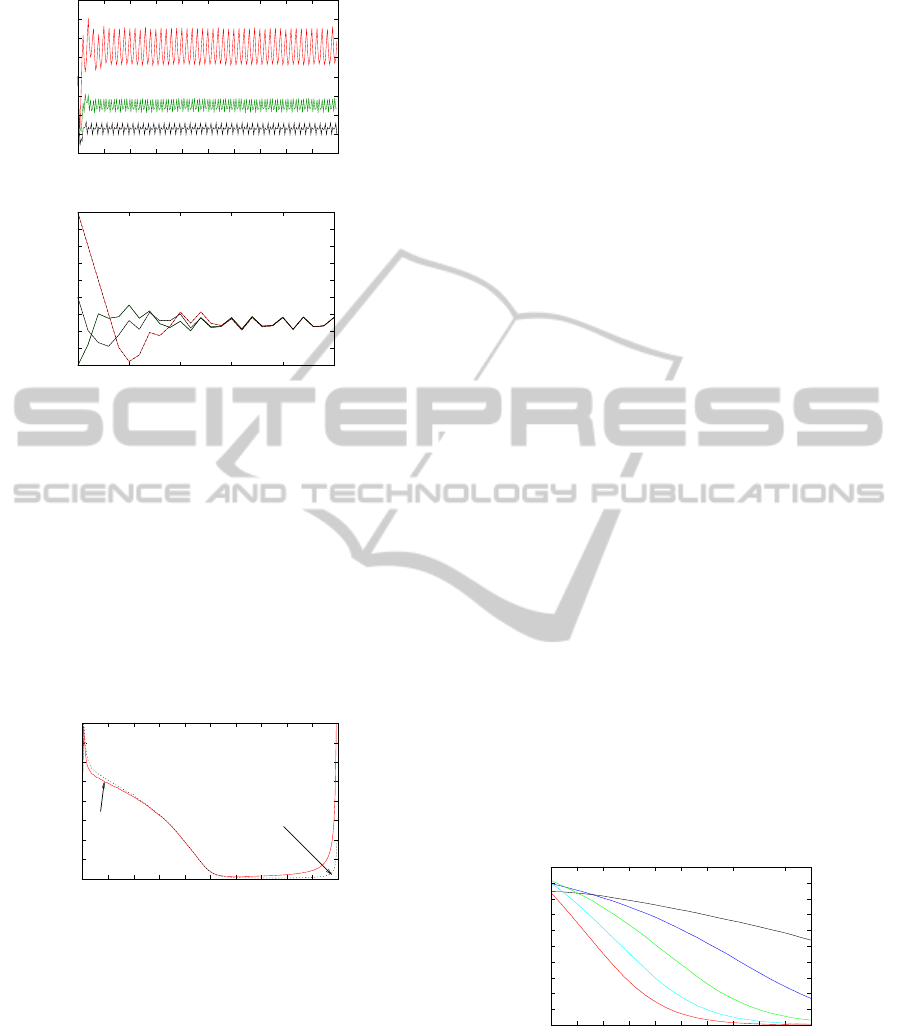
Starting energy=30%

Adaptive Threshold

Fraction of Total Mission Time

Starting energy=20%

Starting energy=10%

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

(a) Threshold Adaptation

Threshold

Fraction of Mission Lifetime

0 0.02 0.04 0.06 0.08 0.1

(b) Impact of Initial Threshold Value

Figure 3: Threshold Variation with Time.

varies with time. After an initial transient, depending

on the initial value of the threshold (see Figure 3b),

the threshold settles into a fairly narrow range. An

obvious question from this ﬁgure is whether low-pass

ﬁltering the thresholds will have a positive effect on

performance by damping down on the variations. Fig-

ure 4 indicates that any such gains will be minimal:

here, we carry out low-pass ﬁltering by using as the

actual threshold the average of the past ﬁve threshold

values.

Threshold

Starting Energy Ratio

Unfiltered Lowpass Filtered

1.2

1.4

1.6

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

0.6

0.4

0.2

0.8

Figure 4: Impact of Low-Pass Filtering of Threshold.

5 ENERGY HARVESTING

If sensor networks must work indeﬁnitely, they re-

quire some means to harvest energy from the operat-

ing environment. Various approaches have been stud-

ied for this. The most commonly suggested method

for outdoor networks is to use solar cells feeding into

a rechargeable battery or a supercapacitor. Other ap-

proaches include using wind energy and energy from

vibrations, using a piezoelectric transducer.

Any system that harvests energy from the envi-

ronment must be prepared to put up with the inherent

variability in power inﬂow. For example, solar har-

vesting is obviously subject to the diurnal cycle; in

addition, there is the incidence of clouds and dust. To

smooth out these effects, we require an energy store

that can be used to smooth out these variabilities. The

size of the energy store is a design issue; if it is too

small, the system will be highly vulnerable to varia-

tions in power inﬂow; if it is too large, it will be very

expensive.

The sensing model is as described previously. The

energy model is as follows. The sensor has a repos-

itory of energy which is replenished continuously by

energy harvesting and depleted by message transmis-

sion. As before, to simplify our description, we as-

sume that transmission is the dominant energy con-

sumer; computation and sensing are negligible by

comparison. Energy inﬂow is stochastic; the proba-

bilistic laws governing it are assumed to be known to

the user. At each sampling instant, the sensor deter-

mines whether or not its datum is worth transmitting

based on the energy available to it and the error that

would result at the base station from not transmitting.

We present here an adaptive thresholding algo-

rithm and compare it against a baseline greedy al-

gorithm. The parameter statistics are assumed to be

unknown. We continue to study adaptive threshold-

ing algorithms when the parameter statistics are un-

known. Perhaps the simplest adaptive thresholding

algorithm is to increment the threshold at a sampling

point whenever the energy store is empty (deﬁned as

being too small to support even one data transmis-

sion), and to decrement it when the energy store is

full. Such an approach does not require one to keep

track of energy inﬂows or outﬂows: only the amount

of energy stored at any given moment (which can eas-

ily be measured).

D_max=3

Storage Capacity=5

Adaptive to Baseline Energy Ratio

Mean Power Inflow

α=1

0.6

0.7

0.8

0.9

0.2 0.3 0.4 0.5 0.6 0.7

α=1/4

α=1/5

α=1/3

α=1/2

0.4

0.3

0.2

0.1

0.5

Figure 5: Performance of Thresholding Algorithm.

Figure 5 shows the performance of this algorithm

relative to the baseline. The power inﬂow is in units

of transmission energies per sampling interval; we as-

sume in this simulation that the inﬂow is normally

distributed with standard deviation equal to the mean,

and conditioned on falling in the interval [0,2µ] where

ICINCO2012-9thInternationalConferenceonInformaticsinControl,AutomationandRobotics

480

µ is the mean.

For very small power inﬂows, there is no real

advantage over the baseline algorithm: the system

is energy-starved. As power inﬂows increase, the

performance improves markedly as compared to the

baseline. The algorithm becomes more effective com-

pared to the baseline as the deviations of the underly-

ing sampled variable are more clustered around 0 (i.e.,

small values of α) and less effective when the devia-

tions are uniformly distributed over ±D

max

(α = 1).

6 DISCUSSION

We have developed lightweight algorithms to keep

the minimum accuracy at the base station as balanced

as possible over the given period of operation. The

aim is to pace the sensor transmissions appropriately

given the energy constraints. We have considered two

models: one in which there is a ﬁxed energy bud-

get and another in which there is an energy store (a

rechargeable battery or a supercapacitor are the most

convenient options) that is replenished by means of

energy harvesting. Such an approach is likely to be

useful in applications involving long-term environ-

mental monitoring.

ACKNOWLEDGEMENTS

This research was partially supported by the National

Science Foundation under grant CNS-0931035. The

author thanks the reviewers for their helpful com-

ments.

REFERENCES

H. Ahmadi and T. Abdelzaher, (2009) “An Adaptive-

Reliability Cyber-Physical Transport Protocol for

Spatio-Temporal Data,” IEEE Real-Time Systems

Symposium.

S. Chalasani and J. M. Conrad, (2008). “A Survey of

Energy Harvesting Sources for Embedded Systems,”

IEEE SoutheastCon, pp. 442–447.

M. H. DeGroot, (2004). Optimal Statistical Decisions, Wi-

ley.

A. Deshpande, C. Guestrin, S.R. Madden, J.M. Hellerstein,

and W. Hong, (2004). “Model-Driven Data Acquisi-

tion in Sensor Networks,” 30th VLDB Conference.

M. Domine, (1995). “Moments of the First Passage Time

of a Wiener Process with Drift Between Two Elastic

Barriers,” Journal of Applied Probability, Vol. 32, No.

4, pp. 1007–1013.

S. Goel and T. Imielinski, (2001). “Prediction-Based Moni-

toring in Sensor Networks,” ACM Computer Commu-

nications Review, Vol. 31, No. 5.

Q. Han, S. Mehrotra, and N. Venkatasubramanian, (2007).

“Application-aware Integration of Data Collection and

Power Management in Wireless Sensor Networks,”

Journal of Parallel and Distributed Computing, Vol.

67, pp. 992–1006.

A. Kansal, J. Hsu, S. Zahedi, and M.B. Srivastava, (2007).

“Power Management in Energy Harvesting Sensor

Networks,” ACM Transactions on Embedded Comput-

ing Systems, Vol. 6, No. 4, September 2007, Article

32.

C. M. Krishna, (2011). “Managing Battery and Supercapac-

itor Resources for Real-Time Sporadic Workloads,”

IEEE Embedded Systems Letters, Vol. 3, No. 1, pp.

32–36.

C. Moser, D. Brunelli, L. Thiele, and L. Benini, (2007).

“Real-Time Scheduling for Energy Harvesting Sensor

Nodes,” Real Time Systems, Vol. 37, pp. 233–260.

G. Park, C. R. Farrar, M. D. Todd, W. Hodgkiss, and T. Ros-

ing, (2007). “Energy Harvesting for Structural Health

Monitoring Sensor Networks,” Los Alamos National

Labs, LA-14314-M5, February 2007.

S. M. Ross, (1970). Applied Probability Models with Op-

timization Applications, New York: Dover Publica-

tions, 1992.

S. Santini and K. Romer, (2006). “An Adaptive Strategy

for Quality-Based Data Reduction in Wireless Sensor

Networks,” International Conference on Networked

Sensing Systems, pp. 29–36.

M. A. Sharaf, J. Beaver, A. Labrinidis, and P.K. Chrysan-

this, (2004). “Balancing Energy Efﬁciency and Qual-

ity of Aggregate Data in Sensor Networks,” VLDB

Journal, Vol. 13, No. 4, December 2004, pp. 384–403.

V. Sharma, U. Mukherjee, and V. Joseph, (2010). “Optimal

Energy Management Policies for Energy Harvesting

Sensor Nodes,” IEEE Transactions on Wireless Com-

munications, Vol. 9, No. 4, p. 1326.

AdaptiveDataUpdateManagementinSensorNetworks

481