Inverting Thanks to SAT Solving

∗

An Application on Reduced-step MD⋆

Florian Legendre

, Gilles Dequen

and Micha¨el Krajecki

UFR Sciences, University of Reims Champagne-Ardennes, Moulin de la Houssse, Reims, France

MIS, University of Picardie Jules Verne, Amiens, France

Keywords:

Logic, Cryptanalysis, Hash Function, MD5, Satisﬁability.

Abstract:

The SATisﬁability Problem is a core problem in mathematical logic and computing theory. The last decade

progresses have led it to be a great and competitive approach to practically solve a wide range of industrial

and academic problems. Thus, the current SAT solving capacity allows the propositional formalism to be an

interesting alternative to tackle cryptanalysis problems. This paper deals with an original application of the

SAT problem to cryptanalysis. We thus present a principle, based on a propositional modeling and solving, and

provide details on logical inferences, simpliﬁcations, learning and pruning techniques used as a preprocessor

with the aim of reducing the computational complexity of the SAT solving and hence weakening the associated

cryptanalysis. As cryptographic hash functions are central elements in modern cryptography we choose to

illustrate our approach with a dedicated attack on the second preimage of the well-known MD⋆ hash functions.

We ﬁnally validate this reverse-engineering process, thanks to a generic SAT solver achieving a weakening of

the inversion of MD⋆. As a result, we present an improvement of the current limit of best practical attacks on

step-reduced MD4 and MD5 second preimage, respectively up to 39 and 28 inverted rounds.

1 INTRODUCTION

The SATisﬁability Problem (short for SAT) is a well-

known decision NP-Complete problem (Cook, 1971).

The interest in studying SAT has grown signiﬁcantly

over the last years because of its conceptual simplic-

ity and ability to express a large set of various prob-

lems. Within a practical framework, a lot of works

highlight SAT implications in ”real world” problems

as diverse as planning (Kautz and Selman, 1996),

model checking (Biere et al., 2006), VLSI design and

also cryptography (Potlapally et al., 2007; Massacci

and Marraro, 2000) ... In recent years, several im-

provements dedicated on the one hand, to the original

backtrack-search DLL procedure (Davis et al., 1962),

and on the other hand to the logical simpliﬁcation

techniques (Bacchus and Winter, 2003) have allowed

SAT solvers to be very efﬁcient in solving huge prob-

lems from industrial areas (Zhang et al., 2001). In

addition cryptography remains ubiquitious and cryp-

tographic primitives (cryptosystems) play a key role

in computer security. Cryptanalysis usually refers to

all techniques that measure the security of a primi-

tive with a view to ﬁnding weaknesses in it that will

∗

This work is partly supported by DGA

facilitate the retrieval any of secret information. Sev-

ral general approaches have been proposed over the

years such as differential (Biham and Shamir, 1990)

or linear (Matsui and Yamagishi, 1992) ones. This

paper focuses on a particular type of algebraic crypt-

analysis which consists in measuring the security of a

cryptosystem thanks to a two-steps process following

a boolean modeling and then a dedicated SAT solving.

This was ﬁrst described in (Massacci and Marraro,

2000) and named logical cryptanalysis. The model-

ing phase is to express, in extenso and independently

from the solving phase, the algorithmic process asso-

ciated to a cipher primitive, a hash function or more

generally a dedicated attack, to a set of boolean equa-

tions (a SAT formula) describing the whole process

where the sequentiality disappeared. In this way, the

solving phase is to estimate the security of the SAT

modeled attack by ﬁnding a solution thanks to a SAT

solver.

1.1 About Logical Cryptanalysis

Recent tremendous progresses of the SAT community

on practical solving allowed some promising logi-

cal cryptanalysis results. First, (Massacci and Mar-

339

Legendre F., Dequen G. and Krajecki M..

Inverting Thanks to SAT Solving - An Application on Reduced-step MD*.

DOI: 10.5220/0004077603390344

In Proceedings of the International Conference on Security and Cryptography (SECRYPT-2012), pages 339-344

ISBN: 978-989-8565-24-2

 2012 SCITEPRESS (Science and Technology Publications, Lda.)

raro, 2000) proposed a ﬁrst logical cryptanalysis at-

tack on the U.S. Data Encryption Standard algorithm.

The idea was to ﬁnd out the cipher key by instanc-

ing the variables corresponding of input/output plain-

texts thanks to a SAT encoding of the stream cipher.

Afterwards, (Mironov and Zhang, 2006) modeled a

whole differential path for the best known hash func-

tions (MD⋆ and SHA-⋆) into a boolean circuit and ob-

tained conclusive results by using some of the best

SAT engines. In (De et al., 2007), the authors tack-

led the second preimage of reduced version of MD4

and MD5. Their encoding enables them to break

the second preimage of 28-step-reduced MD4 and a

26-step-reduced MD5 thanks to SAT solving. They

also improved their attack against a 39-step-reduced

MD4 by adding some information from the Dob-

bertin’s attack (Dobbertin, 1996). Attacks on pseudo-

preimage (Sasaki and Aoki, 2008; Aumasson et al.,

2008) or partial pseudo-preimage (Leurent, 2008) are

a hopeful way to weaken cryptographic functions. Fi-

nally, note to date the best results of MD⋆ cryptanaly-

sis remain attacks by collisions (Wang and Yu, 2005;

Kl´ıma, 2005; Yu and Wang, 2007; Wang et al., 2009).

1.2 Our Approach

This paper deals with a logical cryptanalysis of hash

functions of MD⋆ family. The main contributions are

about SAT encoding of the MD4 and MD5 primitives

on which we apply some logical inference rules. We

then illustrate our approach by improving, than to par-

allel SAT solving, the current limit of best practical

attacks on step-reduced MD4 and MD5 second preim-

age, respectively up to 39 and 28 inverted steps.

The paper is organized as follows: In section 2,

we present some deﬁnitions and outline the beneﬁts

of a SAT encoding within the context of the inversion

problem. In section 3, we describe a dedicated SAT

encoding of MD5 hash function. As an illustration of

this technique, we describe the method to obtain an

encoding of a classical adder circuit and then show

how SAT solving can be useful for inverting a hash

function. The section 4 presents some results about

breaking reduced-step MD4 and MD5 thanks to paral-

lel SAT solving. Finally, the section 5 concludes about

our works and opens future works.

2 BACKGROUND

2.1 Brief Overview of the SAT Problem

Let V = { v

, ..., v

} be a set of n boolean vari-

ables. A signed boolean variable is named a literal.

We denote, v

and v

the positive and negative liter-

als referring to the variable v

respectively. The lit-

eral v

(resp. v

) is TRUE (also said satisﬁed) if the

corresponding variable v

is assigned to TRUE (resp.

FALSE). Literals are commonly associated with logi-

cal AND and OR operators respectively denoted ∧ and

∨. A clause is a disjunction of literals, that is for in-

stance v

∨ v

. Hence, a clause is satisﬁed

if at least one of its literals is satisﬁed. A SAT formula

F is usually considered as a conjunction of clauses

and said under Conjunctive Normal Form (CNF). Con-

sequently, F is satisﬁed if all its clauses are satisﬁed.

SAT is the problem of determining if exists an assign-

ment of V on {TRUE, FALSE} such as to make the

formula F TRUE. If such an assignment exists, F is

said SAT and UNSAT otherwise. In the following, 1

(resp. 0) could mean TRUE (resp. FALSE).

In order to solve the SAT problem, two classes of

techniques are commonly used by the community.

• Complete approaches guarantee an answer in a ﬁ-

nite but exponential runtime. These methods are

mainly based on the DLL (Davis et al., 1962) algo-

rithm which consists in a systematic enumeration

of truth assignments thanks to a binary search-

tree. We choose to use this type of solving ap-

proach within the context of this paper.

• Incomplete SAT solving methods are those that

cannot guarantee an answer in a ﬁnite runtime.

Among the incomplete approaches to SAT solv-

ing, one of the most efﬁcient is based on

gsat

and

walksat

algorithms which can be brieﬂy de-

scribed as noisy and greedy searches into the

search-space. The reader should refer to (Biere

et al., 2009) for more details.

2.2 Cryptographic Hash Functions

Cryptographic hash functions are central elements of

modern cryptography. A hash function can be de-

ﬁned as a deterministic process that generates a ﬁxed-

length bit string, usually named digest, from any-

length bit string also named the message. It is com-

monly used for integrity checking of ﬁles or commu-

nications but also in authentiﬁcation protocols. It is

interesting to notice for a given message, a crypto-

graphic hash function computes a unique digest. On

the other hand, a single digest could be associated to

several messages. Two different messages hashing the

same digest is a collision. Finally, a process that leads

to yield a message from a given digest faster than ex-

haustive search is a preimage attack.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

340

2.3 About MD5

MD5 was designed in 1991 by Ron Rivest as an

evolution of MD4, strengthening its security by

adding some improvements. The operating princi-

ple of this function is based on the Merkle-Damgard

model (Merkle, 1989; Damg˚ard, 1989) and consists

in a hashing process where four states are initialized

and then modiﬁed at each of the 64 steps.

The compression function is required to satisfy

three properties : (i) Collision Resistance, (ii) Second

Preimage Resistance and (iii) Preimage Resistance.

A step is determined as follows :

← S

i−4

+ f(S

i−1

, S

i−2

, S

i−3

) + W[j] + T[i]

← S

≪ r

← S

+ S

i−1

, i ∈ { 1, ..., 64 }

where :

• S

is the current state. S

−3

, S

−2

, S

−1

, S

are the IV.

• W[ j] is the j

word of 32 bits, j ∈ { 0, 1, ..., 15 },

from the input message.

• T[i] among 64 predeﬁned constants

• f a non-linear function ∈ { F, G, H, I }

• ≪ r

the circular shifting to the left(rotating) by r

bits position.

The non-linear functions are deﬁned by:

F(x,y,z) = (x ∧ y) ∨ (x ∧ z) ; G(x,y,z) = F(z,x,y)

H(x,y,z) = x ⊕ y ⊕ z ; I(x,y,z) = y ⊕ (x ∨ z)

More generally, a step computation merely con-

tains an addition of four operands, a circular shifting

to the left and an additionof two operands (See Fig.1).

At the end of the process, an ultimate addition be-

tween the last states and the initial values is computed.

From this results the MD5 digest.

Non linear

function

i-2

i-1

i-3

W[m] T[j]

Figure 1: Hashing process of MD5.

3 ABOUT SAT ENCODING OF MD5

Even, if few works exists on this subject, a good mod-

eling can be crucial to decrease the runtime of a SAT

instance. This section is about the SAT encoding of

the well-known MD5 function.

3.1 Some Logical Simpliﬁcations

SAT can be seen as a tool allowing to express any

problem thanks to boolean equations. The solving

of such an instance is achieved with a dedicated SAT

engine (also named solver) that deals with reasoning

techniques from I.A. Within this framework, infor-

mation is treated by adding pertinent clauses and

removing redundant information thanks to logical

simpliﬁcations. Consider the formula F having

the following clauses, and look at three interesting

logical simpliﬁcations:

= (a∨ b) c

= (b∨ c)

= (c∨ d) c

= (a∨ d ∨ e)

= (b∨ c∨ f) c

= (e∨ f ∨ g)

• Observe that c

is equal to (c

∨ f). In this case,

contains as much information as c

and if c

satisﬁed, necessarily c

is satisﬁed too. This well-

know process is called a subsumption, and since

subsume c

, c

is withdrawn.

• Now focus on c

and c

and note these clauses dif-

fer only in the signedness of the variable g. This

scheme is known as resolution. From this spe-

cial scheme, a new clause named resolvent can

be generated and consists of all the variables of

the two previous clauses except the one that dif-

fers in signedness. Hence, we can add the clause

= ( f ∨ g). c

contains as much information

as in c

and c

. Moreover, in that case, c

sub-

sumes both c

and c

and could be helpful within

the solving.

• Finally, note if a =FALSE then by propagation

b = c = d = e =FALSE. In this sense, we have

(a ⇒ e) and its corresponding clause (a ∨ e).

This is a pertinent clause to add, because it repre-

sents also the relation (e ⇒ a) and before adding

it, from e it was impossible to deduce something

about a.

Regarding MD5, the hashing process is composed of

three operations: an addition of four operands, a cir-

cular shifting and an addition of two operands. We de-

scribe an encoding of each of these components into

the most compressive expression. A noteworthy point

by modeling MD5 into a SAT formula is that the gen-

erated instance keeps starting features from the initial

cipher function, especially its behavior, its statistical

data and its cryptanalytic weaknesses.

3.2 The Addition of Two Operands

To implement the addition of two operands, we di-

rectly express into SAT clauses the logical rules as-

InvertingThankstoSATSolving-AnApplicationonReduced-stepMD*

341

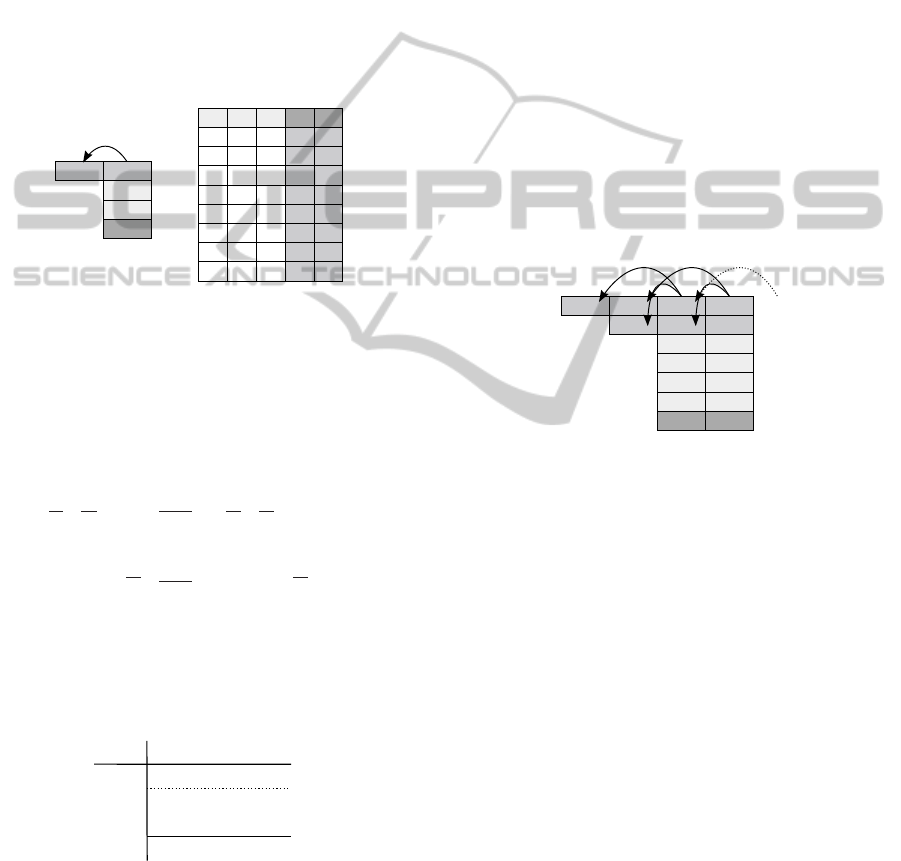
sociated to the classical arithmetical addition. In

this sense, and considering a simple adder circuit,

this can be seen as two operations of implications:

(operands) ⇒ (sum) and (operands) ⇒ (carries). A

modeling of this simple adder is presented on Fig.2,

where s

corresponds of the sum of a

and b

, and c

i+1

is the ouput carry generated by this addition. Arrows

represent generation of carries, from one adding col-

umn to the corresponding next one. Based on this

model, we set up the associated boolean truth table.

In white cases, the input variables and in gray, the

output variables. Finally, this table describes the in-

ference rules that deﬁne the reasoning of an addition

of two operands. Then, we conclude in a generation

i+1

00 0

00 1 1

10 0 1

i+1

10 1 0

01 0 1

01 1 0

11 0 0

11 1 1

Figure 2: Model of an addition of two operands and its core-

sponding truth table of two 1-bit operands.

of SAT equations, where from each line of the table

corresponds two clauses (one clause to each output

variable). For instance, let c

, a

, b

, c

i+1

, s

be ﬁve

boolean variables, the second line of the table in Fig.2

can be read as c

= 0, a

= 0, b

= 1 implies c

i+1

= 0

and s

= 1. This can be formulated as follows:

∧ a

∧ b

⇒ c

i+1

) ∧ (c

∧ a

∧ b

⇒ s

)

And then:

∨ a

∨ b

∨ c

i+1

) ∧ (c

∨ a

∨ b

∨ s)

This type of algebraic modelisation leads to lost

the notion of temporality during the solving process.

We propose to illustrate this crucial point with an in-

stance of a 4 bits addition with holes. We denote by

the variable x ∈ {c, a, b, s} at the index i.

op a

op b

sum s

3 12 0

Index

car c

Figure 3: Holed addition of two binary operands.

Mathematically, looking at the Fig.3 it is quite

easy to see a ≥ 100

(2)

, b ≥ 10

(2)

, either a or b is odd

and s ∈ {((1)1101)

(2)

, ((1)1111)

(2)

}. However, it is

not so easy to export something from the row of the

carries because c depends of a, b and c. Note also

that work in binary ﬁeld leads to have a very detailed

notion of carries while it’s not the case from a larger

scale. Moreover, in SAT, as the reasoning is logical

we deduce some other bits. Firstly, from c

and s

we can deduce c

= 0 and from c

, a

and s

, we can

infer c

= b

= 1. Accordingly, only four solutions

stay possible:

(a, b) ∈ {(0110, 0111)

(2)

, (1110, 1111)

(2)

(0111, 0110)

(2)

, (1111, 1110)

(2)

}

3.3 Modeling the Four Operands

Addition

To implement the four operands addition we need to

consider that two levels of carries is outputed. There-

fore, as for the addition of two operands, carries in

output must be considered as input in the next row.

Consequently, the addition of four operands becomes

an addition of six operands (See Fig.4).

ca1

ca2

ca1

i+1

i-1

ca1

i-1

ca2

i-1

ca2

i+2

ca2

i+1

i-1

Figure 4: Model of an addition of four operands.

3.4 The Non-linear Functions

Anchoredin each of the 64 steps, non-linear functions

are another mean to give rise to chaos and strengthen

to the MD5 cipher. Although the logical formalism

of these functions is an additional constraint to the

cryptanalysts, for us it’s an advantage as we just need

to add them to our modeling.

3.5 Modelisation of MD⋆

Following the previously described method, thanks to

all the bricks we deﬁne, we are able to model the

whole MD5. These components are then cimented

during the generation of clauses thanks to the variable

encoding. Finally, the complete MD5 process consists

in a SAT formula with 12,721 variables and 171,235

clauses. In the same way, we use this framework to

generate SAT formula for the complete MD4 and some

reduced instances for both MD5 and MD4.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

342

4 RESULTS

In order to tackle the second preimage of MD⋆, we

ﬁrst generate a formula representing a reduced-step

process of the hash function and secondly instance

variables corresponding to a particular digest. Thanks

to some of reasoning techniques described in the sec-

tion 3 the formulais preprocessed to decrease its prac-

tical complexity. The resulting formula is then solved

with a SAT engine. In our knowledge, the best prac-

tical result of a second preimage attack of reduced

version MD⋆ is described in (De et al., 2007). They

broke 1 round 12 steps of MD4 and 1 round 10 steps

of MD5. With our approach, we break 1 round 15

steps for MD4 and 1 round 12 steps for MD5 in a few

minutes. Our benchmarks have been achieved on a

Westmere-EP 12 cores thanks to

plingeling

(Biere,

2010) for both MD4 and MD5. Hereafter, some results

input/output values, in big endian, where the digests

correspond to the ones obtained after the last addition

of the MD⋆ algorithm.

1 round 15 steps on MD4

Fixed Hash:

0x00000000 0x00000000 0x00000000 0x00000000

Input found:

0x184937d5 0x6348828c 0x65e7547c 0x0201b903

0xba4f5298 0x12edc6df 0xbbe4a23e 0xa4c25972

0x5d9019f8 0x40bd880b 0x352f6960 0xbcb22ec4

0x43e0debc 0x0a4838d4 0xdf6a3b9f 0xcec88113

1 round 12 steps on MD5

Fixed Hash:

0x01234567 0x89abcdef 0xfedcba98 0x76543210

Input found:

0x0bd86c16 0x6dea158a 0x3fea904c 0x5930a4a1

0xf733709c 0x7e818951 0xdc6f481b 0x21f85c42

0x7a6b2051 0x09762af5 0xbf21286b 0xb70fe9bc

0xb6e76e81 0x0ba31a2c 0x71512697 0xbc2931af

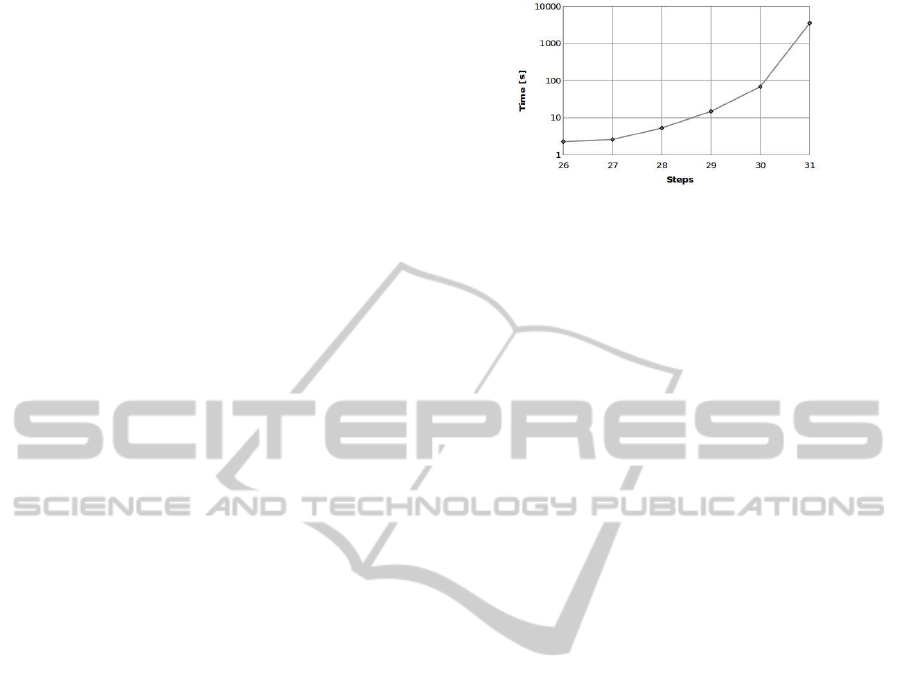
We are also interested in the evolution of the run-

time relative to the number of steps modeled. We

draw these observations in Fig.5, achieved on an av-

erage of several instances.

For both MD4 and MD5 an exponential growth of

the runtime according to the number of steps modeled

is observed. In this manner, these hash functions are

a priori relatively secure against preimage attacks by

SAT SOLVER. However, the solving method presented

in this paper is near from a brute-force attack in that

the generated CNF just represents the hashing process

with a ﬁxed-hash. To improve our results, we should

add some pertinent information to reduce the search

Figure 5: Runtime for solving reduced-step MD4.

space. In this way, we transpose the Dobbertin’s al-

gebraic attack (Dobbertin, 1996) to our reduced-step

MD4 formulae.

Improving Attacks

A good mean to improveour preimage attack is to use

some tricks of crytanalysts. As in (De et al., 2007),

we used the Dobbertin’s attack by instantiating some

variables. More precisely, let be Q

, the modiﬁed state

at the step i ∈ {1, ..., 64}, and M

the j

input 32-bit

sub-block, j ∈ {0, ..., 15}. We ﬁxed:

• Q

, Q

0x00000000

• M

, M

0xa57d8667

By propagation, we also have:

• Q

, Q

0x00000000

The instance is preprocessed, reduced to its most

compacted expression and

plingeling

is then appli-

cated in order to ﬁnd a solution. Our best result for

MD4 was improved from 1 round 12 steps to 2 rounds

7 steps. Hereafter an example of a input/output value.

2 rounds 7 steps on MD4

Fixed Hash:

0x00000000 0x00000000 0x00000000 0x00000000

Input found:

0x321838cd 0x67867da5 0x67867da5 0x4bd844ff

0x67867da5 0x67867da5 0x67867da5 0x60babe30

0x67867da5 0x67867da5 0x67867da5 0x2e731890

0xb84655eb 0x1094c071 0xce0cfe36 0x0252233c

We focus on the evolution of the runtime of

our solved instances and note the representative

curve is very special. Indeed, there is a gap between

steps 35 and 36, then the runtime is quasi-linear to

39 steps and a gap is again observed to up to 40

steps (unsolved after several hours of computation).

This is due to the search space is correlated to the

steps affected by the Dobbertin’s attack. In fact,

Dobbertin’s attack ﬁx some input sub-blocks that

appear at steps 34, 35, 37, 38, 39, 41,. . . Note, steps

InvertingThankstoSATSolving-AnApplicationonReduced-stepMD*

343

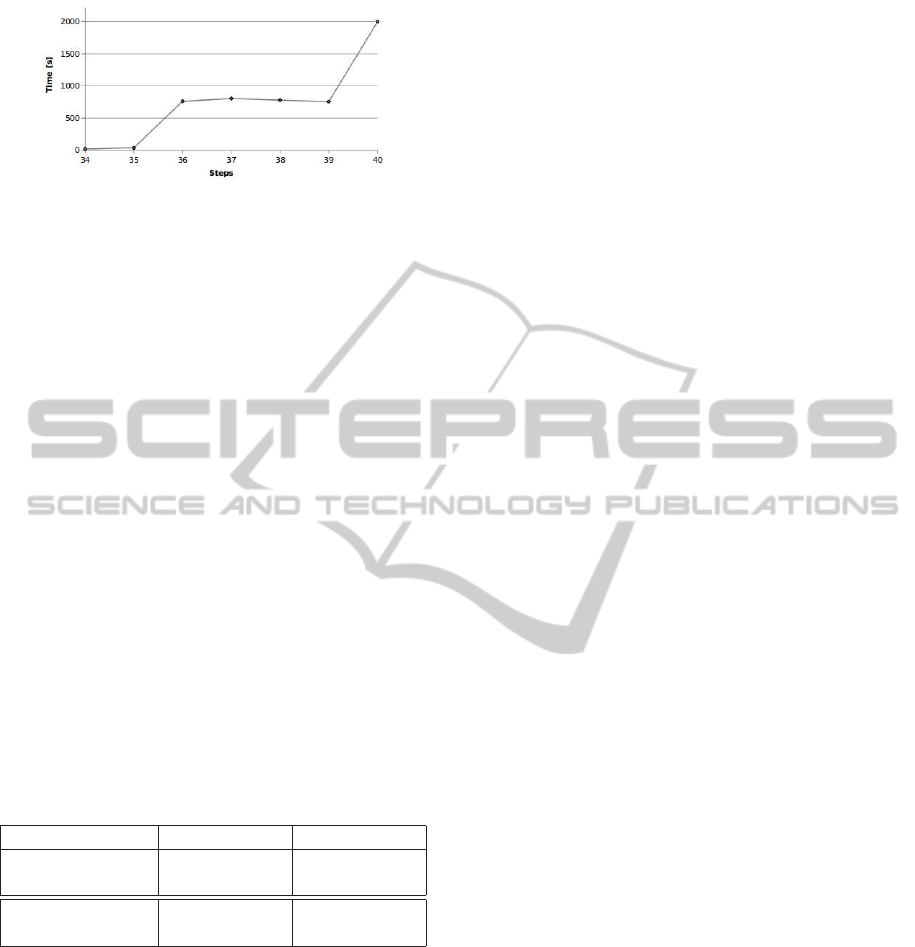
Figure 6: Runtime for reduced-step MD4 + Dobbertin’s at-

tack.

36 and 40 are not in this set that is why constraints

are more numerous and the search space is decreased.

5 CONCLUSIONS

In this paper, we considered second preimage attack

against MD⋆. Our work is based on logical cryptanal-

ysis and described a two phases approach. As a result,

we broke step-reduced instances for both MD4 and

MD5 and improved results in existing practice (See

Table.1). Since many other hash functions like RIPE-

MD, TIGER, SHA-⋆ are built on the same schema as

MD4, our angle of view is hopeful to be generalized.

Indeed, we show an application of SAT as a great tool

to cryptanalyse hash functions. Furthermore, our in-

stance combined with added information led us to be-

lieve we could improve our attack. From our studies

or from the literature about MD⋆, we can adapt and

exploit weaknesses of hash functions to enrich our re-

verse engineering.

Table 1: Practical attacks on step-reduced MD4 and

MD5 second preimage.

Type of CNF In [*] Our attack

MD4 Brute force 28 steps 31 steps

MD4 + info up to 39 steps up to 39 steps

MD5 Brute force 26 steps 28 steps

MD5 + info X X

[*] (De et al., 2007)

REFERENCES

Aumasson, J., Meier, W., and Mendel, F. (2008). Preim-

age attacks on 3-pass haval and step-reduced md5. In

Selected Areas in Cryptography, pages 120–135.

Bacchus, F. and Winter, J. (2003). Effective preprocessing

with hyper-resolution and equality reduction.

Biere, A. (2010). Lingeling, plingeling, picosat and pre-

cosat at sat race 2010. In Tech. Rep. 10/1, FMV Re-

ports Series, Johannes Kepler University, Altenberg-

erstr. Linz, Austria, pages 244–257.

Biere, A., Heljanko, K., Junttila, T., Latvala, T., and Schup-

pan, V. (2006). Linear encodings of bounded LTL

model checking. Logical Methods in Computer Sci-

ence.

Biere, A., Heule, M. J. H., Maaren, H. V., and Walsh, T.,

editors (2009). Handbook of Satisﬁability, volume

185 of Frontiers in Artiﬁcial Intelligence and Appli-

cations. IOS Press.

Biham, E. and Shamir, A. (1990). Differential cryptanalysis

of des-like cryptosystems. In CRYPTO, pages 2–21.

Cook, S. A. (1971). The Complexity of Theorem Proving

Procedures. In 3

ACM Symp. on Theory of Comput-

ing, Ohio, pages 151–158.

Damg˚ard, I. (1989). A design principle for hash functions.

In CRYPTO, pages 416–427.

Davis, M., Logemann, G., and Loveland, D. (1962). A Ma-

chine Program for Theorem-Proving. Journal Associ-

ation for Computing Machine, (5):394–397.

De, D., Kumarasubramanian, A., and Venkatesan, R.

(2007). Inversion attacks on secure hash functions us-

ing satsolvers. In SAT, pages 377–382.

Dobbertin, H. (1996). Cryptanalysis of md4. In FSE, pages

53–69.

Kautz, H. and Selman, B. (1996). Pushing the envelope:

Planning, propositional logic and stochastic search. In

Proc. of 30th national AI and 8th IAAI.

Kl´ıma, V. (2005). Finding md5 collisions on a notebook pc

using multi-message modiﬁcations. In IACR Cryptol-

ogy ePrint Archive, page 102.

Leurent, G. (2008). Md4 is not one-way. In FSE, pages

412–428.

Massacci, F. and Marraro, L. (2000). Logical cryptanalysis

as a sat problem. J.Autom.Reasoning, pages 165–203.

Matsui, M. and Yamagishi, A. (1992). A new method

for known plaintext attack of feal cipher. In EURO-

CRYPT, pages 81–91.

Merkle, R. (1989). One way hash functions and des. In

CRYPTO, pages 428–446.

Mironov, I. and Zhang, L. (2006). Applications of sat

solvers to cryptanalysis of hash functions. In SAT,

pages 102–115.

Potlapally, N. R., Raghunathan, A., Ravi, S., Jha, N. K.,

and Lee, R. B. (2007). Aiding side-channel attacks on

cryptographic software with satisﬁability-based anal-

ysis. IEEE Trans. VLSI Syst., 15(4):465–470.

Sasaki, Y. and Aoki, K. (2008). Preimage attacks on step-

reduced md5. In ACISP, pages 282–296.

Wang, X. and Yu, H. (2005). How to break md5 and other

hash functions. In EUROCRYPT, pages 19–35.

Wang, X., Yu, H., Wang, W., Zhang, H., and Zhan, T.

(2009). Cryptanalysis on hmac/nmac-md5 and md5-

mac. In EUROCRYPT, pages 121–133.

Yu, H. and Wang, X. (2007). Multi-collision attack on the

compression functions of md4 and 3-pass haval. In

ICISC, pages 206–226.

Zhang, L., Madigan, C., Moskewicz, M., and Malik, S.

(2001). Efﬁcient conﬂict driven learning in a boolean

satisﬁability solver. In ICCAD, pages 11–16.

SECRYPT2012-InternationalConferenceonSecurityandCryptography

344