
Latent Ambiguity in Latent Semantic Analysis?
Martin Emms and Alfredo Maldonado-Guerra
School of Computer Science and Statistics, Trinity College, Dublin, Ireland
Keywords:
LSA, Dimensionality.
Abstract:
Latent Semantic Analyis (LSA) consists in the use of SVD-based dimensionality-reduction to reduce the high
dimensionality of vector representations of documents, where the dimensions of the vectors correspond simply
to word counts in the documents. We show that that there are two contending, inequivalent, formulations of
LSA. The distinction between the two is not generally noted and while some work adheres to one formulation,
other work adheres to the other formulation. We show that on both a tiny contrived data-set and also on a more
substantial word-sense discovery data-set that the empirical outcomes achieved with LSA vary according to
which formulation is chosen.
1 INTRODUCTION
Latent Semantic Analyis (LSA) is a widely used
dimensionality-reduction technique. Section 2 re-
calls the matrix properities upon which LSA is based
and then section 3 gives details of two different
dimensionality-lowering transformations which may
be based on those properites, which we will term the
R
1
and R
2
representations, and we argue that there is
ambiguity in the literature as to which representation
is intended. Section 4 then shows empirical outcomes
which vary with the adopted formulation.
2 SINGULAR VALUE
DECOMPOSITION
Latent Semantic Analysis (LSA) is based theoreti-
cally and algorithmically on Singular Value Decom-
position (SVD) properties of matrices. The first con-
cerns the existence of a particular decomposition, a
property expressible as the following theorem.
1
Theorem 1 (SVD). if m×n matrix A has rank r, then
it can be factorised as A = USV
′
where:
1. U has the eigen-vectors of A × A
′
for its first r
columns, in descending eigen-value order; these
columns are orthonormal.
1
This follows closely Theorem 18.3 of (Manning et al.,
2008).
2. S has zeroes everywhere, except its diagonal
which has the square roots of the r distinct eigen-
values of U, in descending order, then 0.
3. V has the eigen-vectors of A
′
× A for its first
columns, in descending eigen-value order; these
column are orthonormal.
Without loss of generality once can assume the di-
mensions of the matrices are:
U : m× r, S : r× r, V : n × r
The second essential fact is that the SVD can be
used to derive optimum
2
low-rank approximations of
the orginal A, by truncating the SVD of A to use just
the first k columns of U and V as follows (see again
(Manning et al., 2008))
Theorem 2 (Low rank approximation). If U× S× V
′
is the SVD of A, then
ˆ
A = U
k
× S
k
× V
′
k
is a optimum
rank-k approx of A where
1. S
k
is diagonal with top-most k values from S.
2. U
k
is just first k columns of U.
3. V
k
is just first k columns of V.
U
k
× S
k
× V
′
k
can be termed the ’rank k reduced SVD
of A’.
The HCI/Graph Example. Figure 1 shows a 12× 9
term-by-document matrix, A (ie. rows of A express
terms via their document occurrence, columns of A
express documents via their term occurrence). This
2
Optimality being defined as minimising the sum of
squares of corresponding matrix positions.
115
Emms M. and Maldonado-Guerra A. (2013).
Latent Ambiguity in Latent Semantic Analysis?.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 115-120
DOI: 10.5220/0004178301150120
Copyright
c
SciTePress

A = U
k
= S
k
= V
k
=
c1 c2 c3 c4 c5 m1 m2 m3 m4
human 1 0 0 1 0 0 0 0 0
inter face 1 0 1 0 0 0 0 0 0
computer 1 1 0 0 0 0 0 0 0
user 0 1 1 0 1 0 0 0 0
system 0 1 1 2 0 0 0 0 0
respones 0 1 0 0 1 0 0 0 0
time 0 1 0 0 1 0 0 0 0
EPS 0 0 1 1 0 0 0 0 0
survey 0 1 0 0 0 0 0 0 1
trees 0 0 0 0 0 1 1 1 0
graph 0 0 0 0 0 0 1 1 1
minor 0 0 0 0 0 0 0 1 1
0.22 −0.11
0.20 −0.07
0.24 0.04
0.40 0.06
0.64 −0.17
0.27 0.11
0.27 0.11
0.30 −0.14
0.21 0.27
0.01 0.49
0.04 0.62
0.03 0.45
3.34 0
0 2.54
0.20 −0.06
0.61 0.17
0.46 −0.13
0.54 −0.23
0.28 0.11
0.00 0.19
0.01 0.44
0.02 0.62
0.08 0.53
Figure 1: A term-by-document matrix A, and the components matrices of its rank 2 reduced SVD U
k
S
k
V
′
k
.
term-by-document matrix is used in a number of arti-
cles by the originators of LSA. See (Deerwester et al.,
1990; Landauer et al., 1998). It is based on an artifi-
cial data set concerning two sets of article titles, one
about HCI (titles c1–c5), the other about graph theory
(titles m1–m4). The columns count occurrences of 12
chosen terms. This A has rank 9, and has a SVD de-
composition into U× S× V
′
, where U is 12 × 9, and
V is 9× 9 . See p406 of (Deerwester et al., 1990).
Multiplying U, S and V
′
gives back exactly A. To
the right in Figure 1 the component matrices U
k
, S
k
,
V
k
of its rank 2 reduced SVD are given, whereby
ˆ
A =
U
k
S
k
V
′
k
(see also p406 of (Deerwester et al., 1990)).
3 CONTENDING
FORMULATIONS OF LSA
LSA concerns using the SVD to make lower dimen-
sion versions of the columns of A (or vectors like
these ie. m dimensional ’document’ vectors).
Where d is an m dimensional vector (such as a
column of A), we contend that the literature has ba-
sically two contenders for its SVD-based reduced di-
mensionality version, contenders we shall term R
1
(d)
and R
2
(d).
Definition 1 (R
1
and R
2
document projections). If A
is m× n, and U
k
S
k
V
′
k
is its rank k reduced SVD, and
d is an m dimensional vector, then k-dimensional ver-
sions R
1
(d) and R
2
(d) are defined by
R
1
(d) = d× U
k
(1)
R
2
(d) = d× U
k
× S
−1
k
= R
1
(d) × S
−1
k
(2)
and if d is i
th
column of A and V
i
k
is i
th
row of V
k
(ie. [V(i, 1) . . . V(i, k)]) the above defintions are equiv-
alent to
R
1
(d) = V
i
k
× S
k
(3)
R
2
(d) = V
i
k
(4)
That the alternative formulations in (3) and (4) are
equivalent to the formulations in (1) and (2), for the
case where d is a column of A, is not immediately
apparent. You can show the equivalence of (3) and
(1), that is, d× U
k
= V
i
k
× S when d is the i
th
column
of A starting from the defining SVD equation A =
USV
′
as follows:
A
′
= (USV
′
)
′
= VSU
′
hence A
′
U = VSU
′
U = VS
hence dU
k
= V
k
S
k
The equivalence of (4) and (2), that is, d×U
k
×S
−1
=
V
i
k
when d is the i
th
column of A, follows from the
equivalence of (3) and (1) by post-multiplication by
S
−1
Where A is a m×n matrix, the matrix V
k
of its re-
duced SVD is a n× k matrix. For the example shown
in Figure 1, V
k
has exactly as many rows (9) as there
were column vectors representing documents in the
original term-by-document matrix A. Therein lies the
possibility to identify these rows of V
k
as the reduced
representation of the columns of A. The fact that (2) is
equivalent to (4) leads to the naturally accompanying
assumption that (2) – d× U
k
× S
−1
– is the formula
for projecting an arbitrary document vector d.
On the other hand, where A is a m× n matrix, the
matrix U
k
of its reduced SVD is a m× k matrix, so
its columns are of exactly the size for it to be possible
to take dot products with an m dimensional document
vector, as expressed in (1). For the example shown in
Figure 1 the columns of the matrix U
k
of A’s reduced
SVD are of size 12, the same as that of document vec-
tors. Additionally the columns of U
k
are orthogonal
to each other and of unit length and thus the R
1
for-
mulation is simply the projection onto a new set of
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
116

orthogonal axes defined by the columns of U
k
.
Ultimately the relationship between the R
1
and
R
2
formulations is a simple one of scaling: R
2
(d) =
R
1
(d) × S
−1
. However, since the entries on the diag-
onal of S are not equal, such a scaling changes the es-
sential geometry. In particular, the nearest neighours,
or the set within a certain cosine range of a given vec-
tor d, is not generally preserved under a scaling. For
example, given a scaling which transforms x and y
according to x
′
=
x
2
, y
′
=
y
8
, the table below gives the
coordinates of 3 points before and after the scaling:
a (0, 8) a
′
(0, 1)
b (4, 8) b
′
(2, 1)
c (4, 0) c
′
(2, 0)
and before the scaling b has nearest neighbour a,
whilst afterwards b
′
has nearest neighbour c
′
, on both
the euclidean distance and cosine measures. Machine
learning methods for adapting distance measures are
often predicated on precisely this fact. In view of this,
the R
1
formulation of LSA, as expressed by (1) and
(3) is genuinely different to the R
2
formulation, as ex-
pressed by (2) and (4) and one should expect R
1
and
R
2
to give diverging outcomes when deployed within
a system. We contend that this has been overlooked.
To this end we will consider the work of a number
of authors, arguing that some are adhering to the R
1
formulation and some to the R
2
formulation.
The R
2
formulation of LSA is one presented in
many, fairly widely cited, publications, for example
(Rosario, 2000; Gong and Liu, 2001; Zelikovitz and
Hirsh, 2001), the relevant parts of which are below
briefly noted.
In the notation of (Rosario, 2000), the reduced
rank SVD of the t × d, term-by-document matrix is
T
t×k
S
k×k
(D
d×k
)
T
, with T and D used in place of U
k
and V
k
. This is described (p3) as providing a repre-
sentation in an alternative space whereby
the matrices T and D represent terms and doc-
uments in this new space
and additionally the repesentation of a query is given
(p4) as q
T
T
t×k
S
−1
k×k
. Thus for pre-existing documents
and novel queries, this matches, modulo notational
switches, the R
2
formulations of (4) and (2).
In the notation of (Zelikovitz and Hirsh, 2001), the
SVD of a t × d term-by-document matrix is TSD
T
.
The representation of a query, based on this SVD is
given as
a query is represented in the same new small
space that the document collection is repre-
sented in. This is done by multiplying the
transpose of the term vector of the query with
matrices T and S
−1
Again modulo notational switches, this is the R
2
for-
mulation of (2).
In the notation of (Gong and Liu, 2001), the SVD
of an m× n term-by-sentence matrix is UΣV
T
, and the
SVD is described as defining a mapping which (p21)
projects each column vector i in matrix A
...to column vector Φ
i
= [v
i1
v
i2
. . . v
ir
]
T
of
matrix V
T
thus the i-th column of A is represented by the i-th
row of V, which is the R
2
formulation given in (4).
On the other hand, the R
1
formulation of LSA is
also presented in many, fairly widely cited, publica-
tions, for example (Bartell et al., 1992; Papadimitriou
et al., 2000; Kontostathis and Pottenger, 2006), the
relevant parts of which are below briefly noted.
In the notation of (Bartell et al., 1992) the reduced
rank SVD of a term-by-document matrix is U
k
L
k
A
T
k
,
and their definitions of document and query represen-
tations are (p162)
row i of A
k
L
k
gives the representation of doc-
ument i in k-space. . ..Let the query be en-
coded as a row vector q in R
t
. Then the query
in k-space would be qU
k
These coincide, modulo notational differences, with
the R
1
formulations of (3) and (1).
In the notation of (Papadimitriou et al., 2000) the
reduced rank SVD of a term-by-document matrix is
U
k
D
k
V
T
k
. Then concerning document representation
they have (p220)
The rows of V
k
D
k
above are then used to rep-
resent the documents. In other words, the col-
umn vectors of A (documents) are projected to
the k-dimensional space spanned by the col-
umn vectors of U
k
which coincides, modulo notation, with the R
1
formu-
lations in (3) and (1).
In the notation of (Kontostathis and Pottenger,
2006), the reduced rank SVD of a term-by-document
matrix is T
k
S
k
(D
k
)
T
, with T
k
and D
k
used in place of
U
k
and V
k
. Their definition of query representation
and document representation is (p3)
Queries are represented in the reduced space
by T
T
k
q. ...Queries are compared to the re-
duced document vectors, scaled by the singu-
lar values (S
k
D
T
k
)
These column vector formulations would be a row
vector formulation qT
k
and D
k
S
k
, which, modulo no-
tational differences are the R
1
formulations of (1) and
(3).
On the basis of these works, there would appear
to be an R
1
-vs-R
2
ambiguity in the formulation of
LatentAmbiguityinLatentSemanticAnalysis?
117
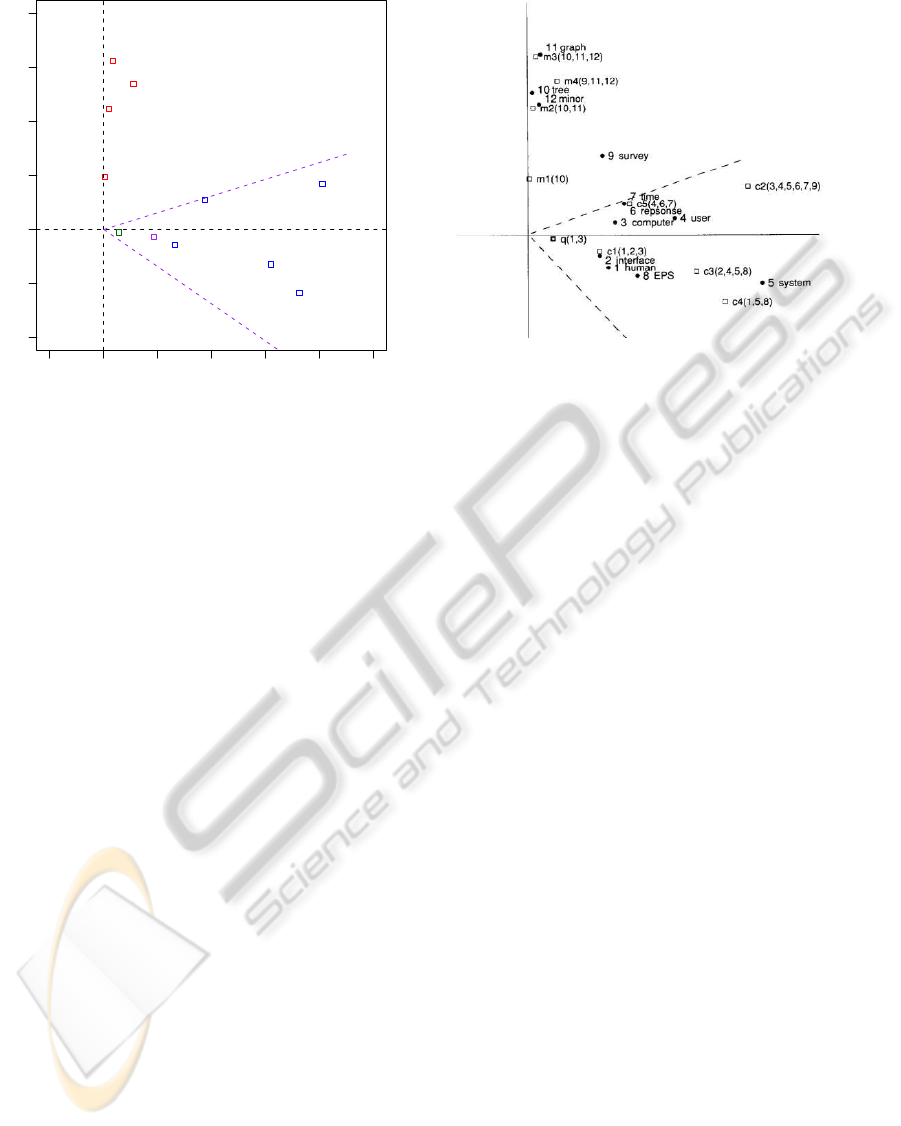
−0.5 0.0 0.5 1.0 1.5 2.0 2.5
−1.0 −0.5 0.0 0.5 1.0 1.5 2.0
c1
c2
c3
c4
c5
m1
m2
m3
m4
q1
q2
Figure 2: Left: shows the R
1
representation of the c1–c5 and m1–m4 documents from Figure 1 and as q1 and q2, the R
1
and
R
2
representations of the query from the text; also shows cosine 0.9 cone around q1 Right screen shot from (Deerwester et al.,
1990), also showing c1–c5, m1–m4 and the query.
LSA, possibly a fairly wide-spread one. Let us now
return to the HCI/Graph example from (Deerwester
et al., 1990). We shall see that there is ambiguity as
to whether it is the R
1
or R
2
representation that is in-
tended by the text of (Deerwester et al., 1990).
Recall that Figure 1 showed the basic term-by-
document matrix for this example, and the component
matrices of its rank-2 reduced SVD. The two dimen-
sional nature of the reduced representations allows for
simple plotting. The left part of Figure 2 plots the 9
documents using the R
1
projection, based on the rank-
2 reduced SVD shown in Figure 1. The positions of
the documents are indicated by boxes labelled ’c’ and
’m’.
To the right in Figure 2 is a reproduction of the
figure on p397 of (Deerwester et al., 1990). Their
plot shows (amongst other things) a reduced repre-
sentation of the documents, as boxes labeled c1-c5
and m1-m4. Whether their plot is intended to depict
the documents in the R
1
or R
2
representation is moot:
the axes in the original plot are not labeled. We have
endeavoured to scale the two plots in such a way that
the document vectors are identically placed in the two
pictures.
In (Deerwester et al., 1990), they consider the
query ’human computer interaction’. Given the terms
chosen for the document vectors, the unreduced vec-
tor q is [1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0]. Applying the
R
1
definition (1), we have R
1
(q) = [0.46, −0.07]
and applying the R
2
definition (2), we R
2
(q) =
[0.14, −0.03]. We have plotted these alternative re-
ductions of q also in the left part of Figure 2, where
they are are shown as q1 and q2.
In the plot reproduced from (Deerwester et al.,
1990) a reduced image of the same query vector was
depicted. Considering their placement of the repre-
sentation of the query relative to the document rep-
resentations, and comparing it to our own placment
of its R
1
and R
2
representation relative to the R
1
rep-
resentations of the documents, it seems the only in-
terpretation that can be put on the plot from (Deer-
wester et al., 1990) is that it shows the documents in
the R
1
projection, but the query in the the R
2
projec-
tion. Note that because the R
2
representation is sim-
ply a scaling of the R
1
representation, with a different
scaling of each dimension, the relative position of the
document and query points in the plot from (Deer-
wester et al., 1990) is not consistent with all points
being shown in the R
2
representation. To emphasize
this, Figure 3 gives the plot of documents and query
in the R
2
representation, again in such a way that the
documents are positioned identically to the plot from
(Deerwester et al., 1990) and one can see that the
query representations are differently placed.
This seeming equivocation between the R
1
and R
2
projection occurs in the text of (Deerwester et al.,
1990) also. In their notation the SVD of the term-by-
document matrix is TSD
′
, thus using T and D in place
of our U and V. Concerning document representation,
there is (p398)
’the rows of the reduced matrices of singular
vectors are taken as coordinates of points rep-
resenting the documents and terms in a k di-
mensional space’
As we noted above, identifying the rows of V
k
as the
reduced representations of documents means adopt-
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
118
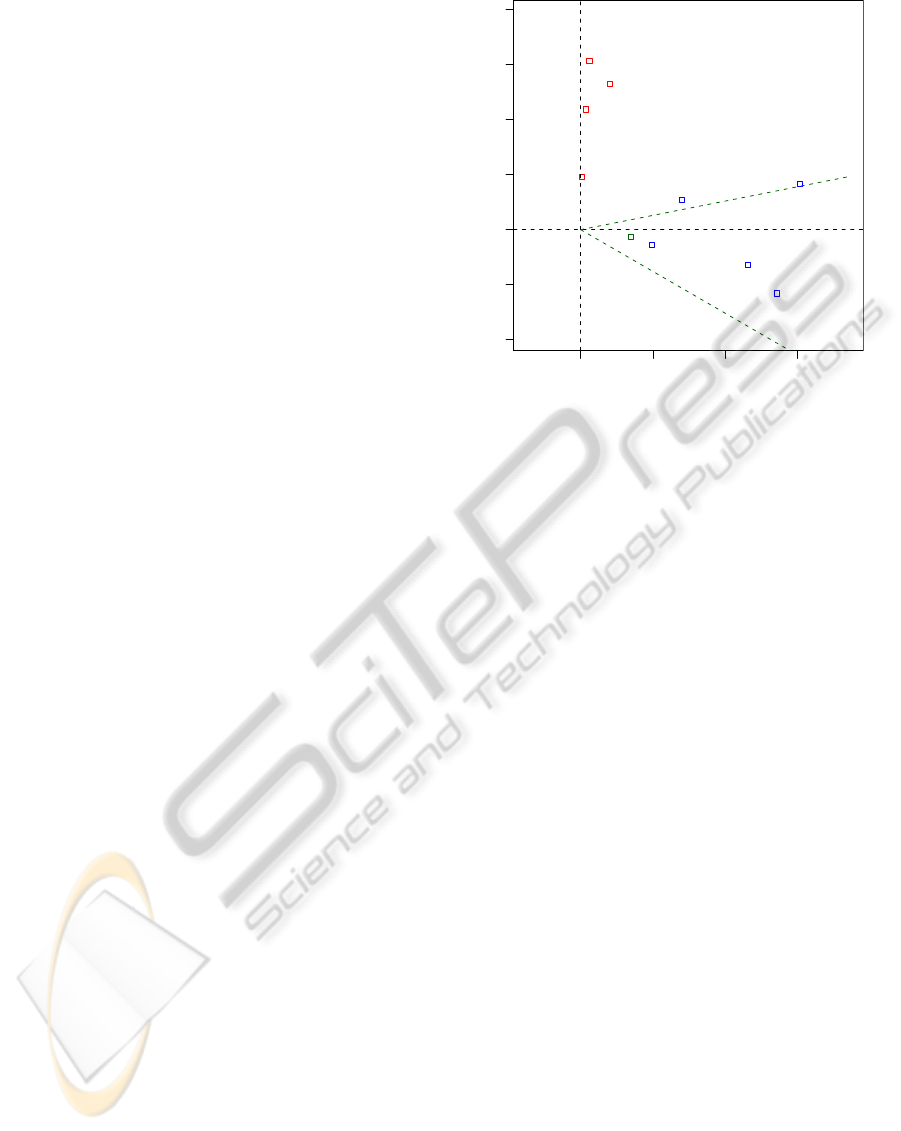
ing the R
2
representation (see (4)). Concerning a
query, if its unreduced representation as a column
vector is X
q
, they give its reduced representation as
X
′
q
TS
−1
, which again, modulo notation, is the R
2
for-
mulation (see (2))
On the other hand p399 has (recall their ’D’ is V
k
in our notation)
so one can consider rows of a DS matrix as
coordinates for documents, and take dot prod-
ucts in this space ... note that the DS space is
just a stretched version of the D space
As we noted above, in equation (3), this amounts to
adopting the R
1
representation for documents.
4 CONTRASTING OUTCOMES
Setting aside these expository details, it is more
important to know whether system outcomes may
change according to which representation, R
1
or R
2
,
is adopted. The LSA dimensionality reduction tech-
nique has been deployed in quite a variety of con-
texts and in each one might investigate the effect of
whether R
1
or R
2
is adopted. In this section we con-
sider two such contexts.
The first context is the original one presented in
(Deerwester et al., 1990): the issue is which docu-
ments should count as similar to a given query un-
der the two representations. Returning again to the
HCI/Graph example, in our R
1
depiction of the docu-
ments and query that is the left-hand plot of Figure 2,
we have also shown a cone which encloses the points
that have a cosine value of 0.9 or higher to R
1
(q). Fig-
ure 3 shows the documents and the query q instead in
the R
2
projection, and shows the corresponding cone
around R
2
(q).
On the R
1
projection, the representations of c1–
c5 are all included in the cone around the query. In
(Deerwester et al., 1990), this inclusion of all the HCI
document representations (c1–c5) within cosine 0.9
of the given query is also noted, notwithstanding the
above-noted R
1
-vs-R
2
ambiguities concerning their
plot of the data. As Figure 3 shows, on the R
2
projec-
tion (of queries and documents), the representations
of c5 and c2 are not included. Note that the visual
similarity of Figure 3 and the left part of Figure 2 is a
bit misleading, as the values on the axes in the R
2
rep-
resentation in Figure 3 are considerably smaller than
those on the axes in the R
1
representation, (by a fac-
tor of 0.29 for the first dimension, and 0.39 for the
second).
Another context in which LSA dimensionality re-
duction has been used is in word clustering. The aim
0.0 0.2 0.4 0.6
−0.4 −0.2 0.0 0.2 0.4 0.6 0.8
c1
c2
c3
c4
c5
m1
m2
m3
m4
q2
Figure 3: The R
2
representation of the c1–c5 and m1–m4
documents from Figure 1 and as q2 the R
2
representation of
the query from the text; also shows cosine 0.9 cone around
q2.
is to cluster occurrences of an ambiguous word into
coherent clusters, clusters each of which reflect a dis-
tinct sense of the word. To this end each occurrence
of an ambiguous term at a position p is represented by
its so-called first-order context vector, C
1
(p), a vec-
tor which for a given uni-gram vocabulary Σ
f
records
for each unigram its frequencyin the windowbetween
p− 10 and p+ 10.
We conducted an experiment making use of the
so-called HILS dataset, which consists of manually
sense annotated occurrences of the four words hard-
interest-line-serve. Thus for each word there is a
sub-corpus consisting of its occurrences, and for each
word, a 60% subset was taken and clustered by the
k-means algorithm, where k is set to the number of
attested senses of the given word. The clustering
is evaluated using the remaining 40% test-set: these
items are first assigned to their nearest cluster centres
and then for each possible sense-to-cluster mapping,
a precision score on the test set is determined, with
the maximum of these reported as the final score.
All so-called non-stopunigrams constitute the fea-
tures of the context vectors. making the context vec-
tors high dimensional: around 10
4
, and before clus-
tering SVD-based dimensionality reduction was ap-
plied. Each of the occurrences of an ambiguous word
is thus treated as a miniature 20 word document to
give a term-by-’document’ matrix, the dimensions of
which were of the order of 10
4
× 10
3
. Then from
this, the reduced rank SVD was calculated for various
percentages of the original dimension size, between
1% and 14%. To give an idea of absolute numbers,
LatentAmbiguityinLatentSemanticAnalysis?
119
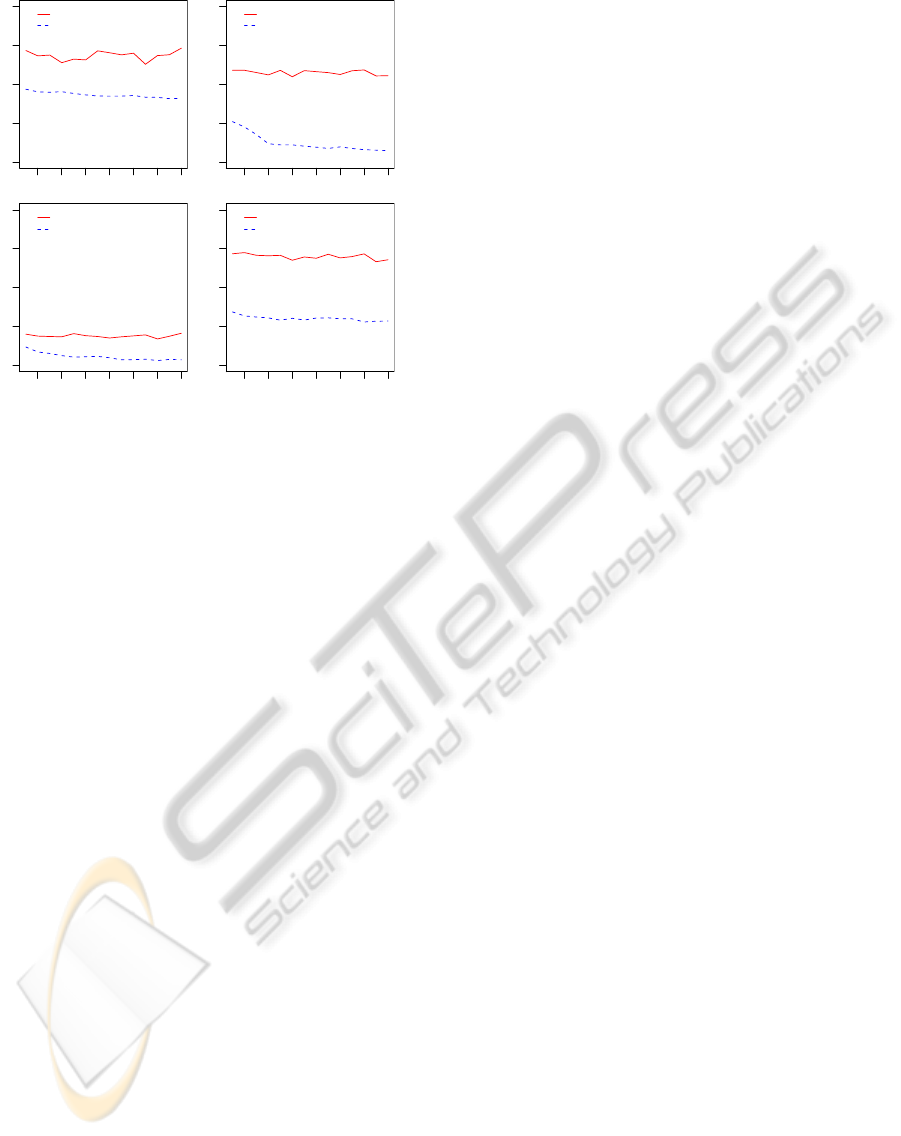
2 4 6 8 10 12 14
20 30 40 50 60
R1
R2
hard
2 4 6 8 10 12 14
20 30 40 50 60
R1
R2
interest
2 4 6 8 10 12 14
20 30 40 50 60
R1
R2
line
2 4 6 8 10 12 14
20 30 40 50 60
R1
R2
serve
Figure 4: Unsupervised clustering results using R
1
and R
2
representations. Vertical axis is accuracy, horizontal axis is
% reduction of dimensions.
for the various words the 10% reduction level corre-
sponds to a dimensionality of 856(hard), 494(inter-
est), 1297(line) and 1304(serve). From these reduced
SVDs, the thereby defined R
1
and R
2
versions of the
context vectors were then used. Figure 4 gives the
results (the 60-40 split was randomly made, and re-
peated 4 times, with the figure summarising the out-
comes over these splits).
This confirms the indications from the tiny 2-
dimensional HCI/Graph example, namely that the
outcomes under the R
1
and R
2
representations are not
identical. In this word clustering context, at each level
of reduction, the outcomes with the R
1
and R
2
repre-
sentations are clearly different. In fact there is a per-
sistent pattern of the R
1
representation giving consis-
tently better outcomes than the R
2
representation.
5 CONCLUSIONS
We have shown that there is a discrepancy amongst
researchers concerning the precise dimensionality re-
duction technique to which they give the name ’LSA’.
The R
1
representation is defined by equations (1) and
(3) whilst the R
2
representation is defined by (2) and
(4), and these alternatives give a different geometry
to the space of reduced representations, manifesting
itself in different nearest-neighbour sets. We showed
that, unsurprisingly, this can lead to different system
outcomes according to which representation, R
1
or
R
2
, is adopted in a given system.
We have not argued for one of these representa-
tions over the other one. Whilst Theorem 2 estab-
lishes that
ˆ
A = U
k
× S
k
× V
′
k
is the optimum rank-k
approximation of A in the sense of minimising the
sum of squared differences between corresponding
matrix positions, there is a good deal of conceptual
clear water between this and consequent ’optimality’
of a particular SVD-based reduction of document vec-
tors in a particular system. This is testified to by the
range of attempts there have been to give a theoretical
justification for an observed system ’optimality’ of a
given deployed SVD-based reduction. Therefore the
R
1
and R
2
alternatives are as theoretically motivated
(or unmotivated) as each other, at least at first glance,
and there is some merit in putting both to the test em-
pirically. What is beyond doubt, though, is that these
R
1
and R
2
altneratives are genuinely different and will
not always give the same empirical outcomes.
REFERENCES
Bartell, B. T., Cottrell, G. W., and Belew, R. K. (1992).
Latent semantic indexing is an optimal special case
of multidimensional scaling. In Proceedings of the
Fifteenth Annual International ACM SIGIR Confer-
ence on Research and Development in Information
Retrieval, pages 161–167. ACM Press.
Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer,
T. K., and Harshman, R. (1990). Indexing by latent
semantic analysis. Journal of the American Scociety
for Information Science, 41(6):391–407.
Gong, Y. and Liu, X. (2001). Generic text summarization
using relevance measure and latent semantic analysis.
In SIGIR, pages 19–25.
Kontostathis, A. and Pottenger, W. M. (2006). A framework
for understanding latent semantic indexing (lsi) per-
formance. Information Processing and Management,
42(1):56–73.
Landauer, T., Foltz, P., and Laham, D. (1998). An introduc-
tion to latent semantic analysis. Discourse Processes,
25(1):259–284.
Manning, C. D., Raghavan, P., and Sch¨utze, H. (2008). In-
troduction to Information Retrieval. Cambridge Uni-
versity Press.
Papadimitriou, C. H., Raghavan, P., Tamaki, H., and Vem-
pala, S. (2000). Latent semantic indexing: A proba-
bilistic analysis. J. Comput. Syst. Sci., 61(2):217–235.
Rosario, B. (2000). Latent semantic indexing: An overview.
Technical report, Berkeley University. available at
http://people.ischool.berkeley.edu/∼rosario/projects/L
SI.pdf.
Zelikovitz, S. and Hirsh, H. (2001). Using lsi for text clas-
sification in the presence of background text. In Pro-
ceedings of CIKM-01, 10TH ACM International Con-
ference on information and knowledge management,
pages 113–118. ACM Press.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
120
