Artificial Intelligence and Creativity
Two Requirements to Solve an Extremely Complex Coloring Problem
Bernd Steinbach
1
and Christian Posthoff
2
1
Institute of Computer Science, Freiberg University of Mining and Technology,
Bernhard-von-Cotta-Str. 2, Freiberg, Germany
2
Department of Computing and Information Technology, The University of the West Indies,
St. Augustine, Trinidad & Tobago
Keywords:
Artificial Intelligence, Creativity, State Space Search, Constraint Satisfaction, Four-valued Edge Coloring,
Complete Bipartite Graph, Rectangle-free Grid, Boolean Equation, SAT-solver, XBOOLE.
Abstract:
The topic of this paper is the rectangle-free coloring of grids using four colors which is equivalent to the edge
coloring of complete bipartite graphs without complete monochromatic subgraphs K
2,2
. So far unsolved are
the grids of the sizes 17× 17, 17× 18, 18× 17, and 18× 18. The number of different 4-color patterns of the
grid 18×18 is equal to 4
324
≈ 1.16798∗10
195
. We summarize in this paper some basic approaches in order to
gain the required knowledge. Three creative approaches are steps so solve the most complex grid of the size
18× 18. Two advanced creative approaches reduce the required runtime to less than 12 percent.
1 INTRODUCTION
We became aware of this problem by chance reading
the publication (Fenner et al., 2009). Because of our
long-time interest and experience in solving binary
problems and in the recent successes in graph color-
ing, set covering, combinatorics on the chess board,
and even Sudoku it was a challenge for us to deal with
this problem.
There are many practical tasks which can be mod-
eled and solved by graph coloring (Marx, 2004). The
colors can be assigned either to the vertices or to the
edges of a given graph. In the paper (Fenner et al.,
2009) the problem is shortly defined as follows. ”A
two-dimensional grid is a set G
n,m
= [n] × [m]. A grid
G
n,m
is c-colorable if there is a function χ
n,m
: G
n,m
→
[c] such that there are no rectangles with all four cor-
ners of the same color.” A rectangle is defined by the
intersection points of two rows and two columns. In
comparison with (Fenner et al., 2009) we exchanged
in this definition the variables m and n to get a natural
alphabetic order of m rows and n columns.
By some theorems it is known that grids 18 × 19,
19 × 18, and 19 × 19 are not 4-colorable, and it was
also known (including examples) that a grid 16 × 16
is 4-colorable. The problem was not solved for the
grids 17× 17,17× 18,18× 17,18× 18.
The set of possible color configurations for the
grid G
18,18
has 4
324
elements because each grid point
can have 1 out of 4 values, and the number of rect-
angles is equal to 23,409. Each rectangle must be
checked four times whether the corner points have
the same color or not. Here a first simplification can
be seen: we only deal with the problem 18× 18, be-
cause a solution for this size gives also solutions for
the smaller sizes, simply by deleting rows or columns,
respectively.
Each solution gives 4! solutions because permuta-
tions of the 4 colors give more solutions. Addition-
ally, any solution gives 18! × 18! solutions, because
the permutations of rows and columns give new so-
lutions again. This means that we have no solution
or a gigantic number of solutions which cannot even
be recorded. However, the number of 4!∗ 18!∗ 18! ≈
9.8 ∗ 10
32
equivalent solutions is negligibly small in
comparison to all 1.16798∗ 10
195
different color pat-
terns of the grid G
18,18
.
2 LOGIC MODELS OF THE
PROBLEM TO SOLVE
Due to the restricted space we refer for our four-
valued model to our paper (Steinbach and Posthoff,
2012a). The next modeling step is the mapping into
411
Steinbach B. and Posthoff C..
Artificial Intelligence and Creativity - Two Requirements to Solve an Extremely Complex Coloring Problem.
DOI: 10.5220/0004183004110418
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 411-418
ISBN: 978-989-8565-39-6
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

Table 1: Mapping of a 4-valued color x to 2 Boolean vari-
ables a and b.
x a b
1 0 0
2 1 0
3 0 1
4 1 1
the Boolean space. This was not necessary for many
other problems, they were binary by nature - a queen
or a bishop was on a field or not etc. Here we express
the four different color values by two Boolean values.
Table 1 shows the used mapping.
Function (1) depends for one rectangle on eight
Boolean variables and has a Boolean result that is true
in the case that the colors in all four corners of the
rectangle selected by the rows r
i
and r
j
and by the
columns c
k
and c
l
are equal to each other:
f
ecb
(a
r
i
,c
k
,b
r
i
,c
k
,a
r
i
,c
l
,b
r
i
,c
l
,
a
r
j
,c
k
,b
r
j
,c
k
,a
r
j
,c
l
,b
r
j
,c
l
) =
(a
r
i
,c
k
· b
r
i
,c
k
· a
r
i
,c
l
· b
r
i
,c
l
· a
r
j
,c
k
· b
r
j
,c
k
· a
r
j
,c
l
· b
r
j
,c
l
)∨
(a
r
i
,c
k
· b
r
i
,c
k
· a
r
i
,c
l
· b
r
i
,c
l
· a
r
j
,c
k
· b
r
j
,c
k
· a
r
j
,c
l
· b
r
j
,c
l
)∨
(a
r
i
,c
k
· b
r
i
,c
k
· a
r
i
,c
l
· b
r
i
,c
l
· a
r
j
,c
k
· b
r
j
,c
k
· a
r
j
,c
l
· b
r
j
,c
l
)∨
(a
r
i
,c
k
· b
r
i
,c
k
· a
r
i
,c
l
· b
r
i
,c
l
· a
r
j
,c
k
· b
r
j
,c
k
· a
r
j
,c
l
· b
r
j
,c
l
).
(1)
The conditions of the 4-color problem on a grid
G
m,n
will be satisfied when the function f
ecb
(1) is
equal to 0 for all rectangles which can be expressed
by
m−1
_
i=1
m
_
j=i+1
n−1
_
k=1
n
_
l=k+1
f
ecb
(a
r
i
,c
k
,b
r
i
,c
k
,a
r
i
,c
l
,b
r
i
,c
l
,
a
r
j
,c
k
,b
r
j
,c
k
,a
r
j
,c
l
,b
r
j
,c
l
) = 0 . (2)
Now we have a logic model for the problem, it
is already more comprehensive than the problem to
solve. It is valid for any value of m and n; if we want,
we can explicitly set m = 18 and n = 18. Any solution
of this equation is a solution of the problem. Here and
in many other AI solutions we are facing a next prob-
lem, the question of the correctness of the solution.
At all 23,409 rectangles must be checked relating the
4 colors for a single color pattern of the grid G
18,18
. A
human being can not be sure that he checked all these
4∗ 23, 409 = 93,636 conditions without any mistake.
Hence, the required 93,636 checks require a next soft-
ware package - the question for the correctness of a
solution is shifted and depends on the correctness of
something else (in this case on the correct working
of some soft- and hardware). Up to now the problem
of correctness cannot be answered at all. The check
of the rectangle condition for a given color pattern by
several independent software programscan reduce the
remaining uncertainness.
3 BASIC APPROACHES AND
RESULTS
In order to solve this coloring problem we need deep
knowledge of its properties. The details of our ba-
sic exploration are published in the paper (Steinbach
et al., 2010). Due to the restricted space, we summa-
rize here the main results in a very compressed man-
ner.
• The Boolean equation (2) could be solved using
XBOOLE (Posthoff and Steinbach, 2004), and
(Steinbach and Posthoff, 2009) for the the grid
G
7,2
within 4.383 seconds. There are already
67,420,672 color patterns of the 4-colored grid
G
7,2
which do not satisfy the rectangle-free con-
dition; that is a ratio of 25.12 %.
• Based on a heuristic which uses a single fixed uni-
form distribution of the colors in the top row and
in the leftmost column the number of Boolean
variables could be enlarged from 28 for G
7,2
to
76 for G
19,2
. That means, by utilizing properties
of the 4-color problem mentioned above, we have
solved problems that are 2
48
= 2.82∗ 10
14
times
larger than before.
• An iterative approach utilizes the DIF -operation
of XBOOLE (Posthoff and Steinbach, 2004), and
(Steinbach and Posthoff, 2009)as shownin Figure
1 for all rectangles expressed by:
|rectangle| =

m
2

∗

n
2

. (3)
• The exchange of space and time allows solve for
4-colored grids which are modeled with up to 384
Boolean variables instead of 76 variables in the
second (already improved) approach. This means
that this approach allows solving problems which
are 2
308
= 5.214812∗ 10
92
times larger than be-
fore.
for(i = 0; i < all_rect; i++)
aps = DIF(aps, f_ecb[i]);
Figure 1: Iterative approach with unrestricted space require-
ments.
We tried to solve the 4-color grid problem using
the best SAT-solvers from the SAT-competitions of
the last years. Equation (2) can be easily transformed
into a SAT-equation by negation of both sides and the
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
412

Table 2: Time to solve quadratic 4-colored grids using different SAT-solver.
time in minutes:seconds
rows columns variables clasp-1.2.0 lingeling plingeling precosat
12 12 288 0:00.196 0:00.900 0:00.990 0:00.368
13 13 338 0:00.326 0:01.335 0:04.642 0:00.578
14 14 392 0:00.559 0:03.940 0:02.073 0:00.578
15 15 450 46:30.716 54:02.304 73:05.210 120:51.739
application of de Morgan’s law to the Boolean expres-
sion on the left-hand side. In this way we get the re-
quired conjunctive form for the SAT-solver (4):
m−1
^
i=1
m
^
j=i+1
n−1
^
k=1
n
^
l=k+1
f
ecb
(a
r
i
,c
k
,b
r
i
,c
k
,
a
r
i
,c
l
,b
r
i
,c
l
,a
r
j
,c
k
,b
r
j
,c
k
,a
r
j
,c
l
,b
r
j
,c
l
) = 1 . (4)
Table 2 shows the required time to find the first
solution for quadratic 4-colored grids G
12,12
, G
13,13
,
G
14,14
, and G
15,15
using the SAT-solver clasp (Geb-
ser et al., 2007), lingeling (Biere, 2010), plingeling
(Biere, 2010), and precosat (Biere, 2010).
From the utilization of the SAT-solvers we learned
that
1. SAT-solver are powerful tools that are able to
solve 4-colored grids up to G
15,15
,
2. it was not possible to calculate a 4-colored grid
larger than G
15,15
directly.
The reasons for the second statement are firstly that
the search space for the 4-colored grid G
16,16
is 4
31
=
4.61 ∗ 10
18
times larger than the search space for the
4-colored grid G
15,15
, and secondly that the fraction
of 4-colorable grids is reduced for the larger grid even
stronger.
4 CREATIVE APPROACHES TO
SOLVE THE PROBLEM
4.1 Restriction to a Single Color of
4-colored Grids
Due to the high complexity, a divide-and-conquer ap-
proach may facilitate the solution of the 4-colored
grid G
17,17
or even the grid G
18,18
. The divide step
restricts first to a single color. At least one fourth of
the grid positions must be covered by the first color
without contradiction to the color restrictions. When
such a partial solution is known, the same fill-up step
must be executed taking into account the already fixed
positions of the grid. This procedure must be repeated
for all four colors.
The advantage of this approach is that a single
Boolean variable describes whether the color is as-
signed to a grid position or not. Such a restric-
tion to one half of the needed Boolean variables re-
duces the search space from 2
2∗18∗18
= 1.16∗ 10
195
to
2
18∗18
= 3.41∗ 10
97
for the grid G
18,18
drastically.
The function f
ecb
(1) which describes equal as-
signments of the four colors in the corners of a rect-
angle can be simplified to f
ecb1
(5) for a single color
in the divide and conquer approach.
f
ecb1
(a
r
i
,c
k
,a
r
i
,c
l
,a
r
j
,c
k
,a
r
j
,c
l
) =
(a
r
i
,c
k
∧ a
r
i
,c
l
∧ a
r
j
,c
k
∧ a
r
j
,c
l
) (5)
By transformation into a SAT problem we get
m−1
^
i=1
m
^
j=i+1
n−1
^
k=1
n
^
l=k+1
f
ecb1
(a
r
i
,c
k
,a
r
i
,c
l
,a
r
j
,c
k
,a
r
j
,c
l
) = 1 .
(6)
A disadvantage of this approach is that the implicit
assignment of exactly one color to each grid position
is lost. The values of the pair of variables (a
r
i
,c
k
,b
r
i
,c
k
)
in the solution of (4) determine one of the four colors
for the position of the row r
i
and the column c
k
. The
value of the single variable a
r
i
,c
k
in the solution of (6)
determines only whether the chosen color is assigned,
a
r
i
,c
k
= 1, or one of the remaining colors must be used
a
r
i
,c
k
= 0.
One solution of (6) calculated by a SAT solver will
be the assignment of values 0 to all a-variables. This
is a correct solution; the chosen color does not con-
flict with the rectangle condition when it is not as-
signed to any grid position. However, we are not in-
terested in this trivial solution; we are looking for a
solution where the chosen color covers one fourth of
the grid positions. Consequently, this approach re-
quires the calculation of all solutions of (6) using a
SAT-solver, and the selection of the solutions with a
maximal number of 1 values which must be detected
by counting. Hence, a SAT solver cannot solve this
problem directly.
4.2 Iterative Greedy Approach for a
Single Color of 4-colored Grids
It is a necessary condition for the rectangle-free 4-
colored grid G
18,18
that at least one fourth 1 values
ArtificialIntelligenceandCreativity-TwoRequirementstoSolveanExtremelyComplexColoringProblem
413

1 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0
1 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0 0 0
1 0 0 0 0 1 1 0 0 0 0 0 0 1 1 0 0 0
0 1 0 1 0 0 0 1 0 0 0 0 0 1 0 1 0 0
0 1 0 0 0 1 0 0 1 0 0 1 0 0 0 0 1 0
0 0 1 0 1 0 0 0 1 0 0 0 0 0 1 1 0 0
0 0 1 0 0 0 1 1 0 0 0 0 1 0 0 0 1 0
0 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 1
0 0 0 0 1 1 0 1 0 0 1 0 0 0 0 0 0 1
1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
0 1 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1
0 0 1 0 0 0 0 0 0 0 0 1 0 1 0 0 0 1
0 0 0 1 0 0 0 0 0 0 1 0 0 0 1 0 1 0
0 0 0 0 1 0 0 0 0 1 0 0 0 1 0 0 1 0
0 0 0 0 0 1 0 0 0 1 0 0 1 0 0 1 0 0
0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 0
0 0 0 0 0 0 0 1 0 1 0 1 0 0 1 0 0 0
0 0 0 0 0 0 0 0 1 0 1 0 1 1 0 0 0 0
Figure 2: Rectangle-free grid G
18,18
colored by one fourth
of all positions with the color 1.
of the 18 ∗ 18 = 324 grid positions are colored with
the same color without violation of the rectangle con-
dition. The main idea for such a check is the itera-
tive extension of maximal single colored grids G
k,k
to
correct single colored grids G
k+1,k+1
and the restric-
tion of the solution set by utilization of permutation
classes. The details of this approach are the topic of
the paper (Steinbach and Posthoff, 2012b). Figure 2
shows the found correct assignment of 81 values 1 to
the 324 grid position of G
18,18
.
Our effort to fill up the 1-colored grid G
18,18
of
Figure 2 with the second color on again 81 grid po-
sitions failed. This results from the fact that the free-
dom for the choice of the positions is restricted by the
assignments of the first color. We learned from this
approach that it is not enough to know a correct col-
oring for one color; these assignments must not con-
strain the assignment of the other colors.
4.3 Cyclic Color Assignments of
4-colored Grids
The smallest restrictions for the coloring of a grid by
four colors are given when the number of assignments
to the grid positions is equal for all four colors. For
quadratic grids G
m,n
with m = n and an even num-
ber of m rows and n columns, quadruples of all grid
positions can be chosen which contain all four col-
ors. There are several possibilities of such selections
of quadruples. One of them is the cyclic rotation of a
chosen grid position by 90 degrees around the center
of the grid. Figure 3 (a) illustrates this possibility for
a simple grid G
4,4
. The quadruples are labeled by the
(a)
r
1
s
1
t
1
r
2
t
4
u
1
u
2
s
2
s
4
u
4
u
3
t
2
r
4
t
3
s
3
r
3
(b)
r
1
s
1
t
1
u
1
r
2
u
4
v
1
w
1
v
2
s
2
t
4
w
4
x
1
w
2
t
2
s
4
v
4
w
3
v
3
u
2
r
4
u
3
t
3
s
3
r
3
Figure 3: Cyclic quadruple in quadratic grids: (a) G
4,4
, (b)
G
5,5
.
letters r,s,t, and u. The attached index specifies the
element of the quadruple.
In addition to the color restriction (6) for the cho-
sen single color we can require that this color occurs
exactly once in each quadruple. This property can be
expressed by two additional rules. For the corners of
the grid of Figure 3 (a), for instance, we model as first
rule the requirement:
r
1
∨ r
2
∨ r
3
∨ r
4
= 1 , (7)
so that at least one variable r
i
must be equal to 1. As
a second rule, the additional restriction
(r
1
∧ r
2
) ∨ (r
1
∧ r
3
) ∨ (r
1
∧ r
4
)∨
(r
2
∧ r
3
) ∨ (r
2
∧ r
4
) ∨ (r
3
∧ r
4
) = 0 (8)
prohibits that more than one variable r
i
is equal to 1.
A SAT-formula can be constructed using (6) and
for all cyclic quadruples as illustrated in Figure 3 (a)
both the fitted requirements (7) and the fitted restric-
tions (8) negated using de Morgan’s laws. Hence, 7
clauses must be added to the SAT-formula for each
quadruple. The solution of such a SAT-formula for a
quadratic grid of even numbers of rows and columns
must assign exactly one fourth of the variables to 1.
Such a solution can be used rotated by 90 degrees for
the second color, rotated by 180 degrees for the third
color, and rotated by 270 degrees for the forth color
without any contradiction.
We generated the cnf-file of this SAT-formula
which depends on 324 variables and contains 23,976
clauses for the grid G
18,18
. The SAT-solver clasp-
2.0.0 found the first cyclic reusable solution for the
grid G
18,18
after 212,301.503 seconds which means 2
days 10 hours 58 minutes 21.503 seconds. Figure 4
(a) shows this solution for the first color of the grid
G
18,18
.
Using the core solution of Figure 4 (a) we have
constructed the 4-colored grid G
18,18
of Figure 4 (b)
by three times rotating around the grid center by 90
degrees each and assigning the next color.
Many other 4-colored grids can be created from
the solution in Figure 4 (b) by permutations of rows,
columns, and colors. Several correct 4-colored grids
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
414

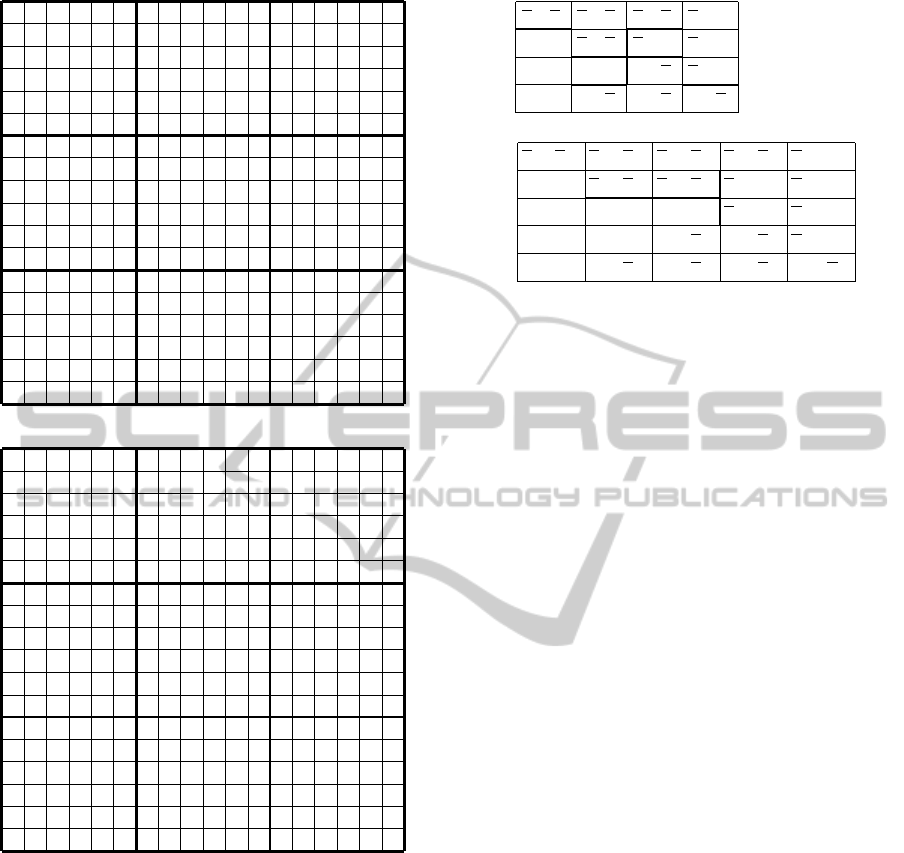
(a)
0 0 1 1 0 0 1 0 0 0 0 0 0 0 1 0 1 0
0 0 0 0 0 0 1 0 0 0 1 1 0 0 0 1 0 1
0 0 0 0 1 0 0 0 0 1 0 1 0 1 0 0 1 0
0 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 0 0
1 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 1
1 1 0 0 0 0 0 1 0 0 0 0 0 0 0 1 1 0
1 0 0 0 1 0 1 0 1 0 0 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 0 0 0 0 1 1 0 0
0 1 0 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0
0 1 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1
0 0 0 0 0 0 0 1 1 1 0 0 0 0 1 0 0 1
0 0 0 1 1 0 0 1 0 0 1 0 1 0 0 0 0 0
1 0 0 0 0 0 0 0 0 0 0 1 1 0 1 0 0 0
0 0 0 0 0 1 0 0 1 0 1 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0 1 0 0 0 1 1 0 1 0 0
0 0 1 0 0 1 0 1 0 0 0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0 0 1 0 0 1 1 0 0 0
1 0 1 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0
(b)
2 4 1 1 4 2 1 3 3 4 4 2 2 2 1 3 1 3
4 2 4 3 3 4 1 3 2 2 1 1 2 4 2 1 3 1
2 4 2 2 1 4 3 4 2 1 3 1 3 1 4 3 1 2
4 1 3 1 3 3 2 4 1 3 4 1 4 2 2 3 4 2
1 3 4 1 4 1 2 3 2 3 2 2 3 1 4 2 4 1
1 1 2 3 2 3 3 1 4 2 2 4 4 2 4 1 1 3
1 4 4 4 1 3 1 3 1 2 3 2 4 3 3 4 2 2
3 4 2 3 1 1 2 2 3 3 3 4 2 4 1 1 4 4
3 1 4 2 2 1 1 2 4 1 4 2 1 3 2 3 3 4
2 1 1 4 1 3 4 2 3 2 4 3 3 4 4 2 3 1
2 2 3 3 2 4 2 1 1 1 4 4 3 3 1 4 2 1
4 4 2 1 1 2 4 1 4 3 1 3 1 3 2 2 2 3
1 3 3 2 4 2 2 4 4 2 3 1 1 4 1 4 3 3
3 2 4 2 3 1 4 4 1 4 1 4 3 2 3 2 1 3
4 2 1 4 4 2 3 2 1 3 2 4 1 1 3 1 3 2
4 3 1 2 3 1 3 1 3 4 2 1 2 3 4 4 2 4
3 1 3 4 2 4 3 3 4 4 1 3 2 1 1 2 4 2
1 3 1 3 4 2 2 4 4 1 1 3 4 2 3 3 2 4
Figure 4: Cyclic colored grid G
18,18
: (a) basic solution for
one color; (b) complete solution by merging the solution of
(a) rotated by 90, 180, and 270 degrees for the other colors.
G
17,18
originate from the 4-colored grid G
18,18
by re-
moving any single row, and by removing any single
column we get 4-colored grids G
18,17
. Obviously,
several so far unknown 4-colored G
17,17
can be se-
lected from the 4-colored grid of Figure 4 (b) remov-
ing both any single row and any single column.
It should be mentioned that the approach of cyclic
reusable single assignments can be applied to 4-
colored square grids of an odd number of rows and
columns, too. The central position must be colored
with the first chosen color. Figure 3 (b) shows the
principle of the quadruple assignment in this case.
(a)
a
3
a
4
a
5
a
6
a
7
a
8
a
3
a
4
a
7
a
8
a
1
a
2
a
1
a
2
a
5
a
6
a
5
a
6
a
1
a
2
a
1
a
2
a
7
a
8
a
3
a
4
a
7
a
8
a
5
a
6
a
3
a
4
(b)
a
5
a
6
a
7
a
8
a
9
a
10
a
11
a
12
a
5
a
6
a
11
a
12
a
1
a
2
a
3
a
4
a
1
a
2
a
7
a
8
a
9
a
10
a
3
a
4
a
3
a
4
a
9
a
10
a
7
a
8
a
1
a
2
a
3
a
4
a
1
a
2
a
11
a
12
a
5
a
6
a
11
a
12
a
9
a
10
a
7
a
8
a
5
a
6
Figure 5: Cyclic Boolean angle encoding of grids: (a) G
4,4
,
(b) G
5,5
.
The SAT-solver clasp-2.0.0 found the first cyclic
4-colorable solution for odd grids up to G
15,15
in less
than 0.6 seconds, but could not solve this task for the
grid G
17,17
until now.
At this point we can state that the combination of
our creativity to select the subproblem of cyclic color
assignments with the AI of the used SAT-solvers al-
lowed to find a rectangle-free 4-colored grid G
18,18
out of the exceptionally large number of 1.16798 ∗
10
195
color patterns. That means that we have solved
the explored problem. For Mathematicians in the area
of bipartite Ramsey numbers we can state: instead of
17 ≤ BR(2, 4) ≤ 19 we have now BR(2,4) = 19.
5 ADVANCED CREATIVE
APPROACHES
5.1 Reduced Cyclic Model
The search space of a SAT-solver depends exponen-
tially on the number of Boolean variables used in the
model. The first key for our successful solution for
the grid G
m,n
with m = n = 18 was the separation of
a subproblem that depends only on m
2
= 18
2
= 324
Boolean variables instead of 2∗m
2
= 2∗ 18
2
= 648 as
needed for the complete grid coloring problem with
four colors. Further restrictions of the needed model
variables may be a source to reduce the calculation ef-
fort in order to find more cyclic solutions in a shorter
period of time.
The source for the further simplification must be
given by the problem to solve itself: the search for a
cyclic rectangle-free coloring for a quadratic grid with
a single color. The quadruples introduced in subsec-
tion 4.3 describe regions in which exactly one of the
four grid elements must be equal to 1. Instead of this
ArtificialIntelligenceandCreativity-TwoRequirementstoSolveanExtremelyComplexColoringProblem
415

1-out-of-4 encoding by four Boolean variables (7), (8)
a direct binary encoding by conjunctions of only two
Boolean variables a
i
,a
j
can be used:
• the angle of rotation is equal to 0 degrees: a
i
a
j
,
• the angle of rotation is equal to 90 degrees: a
i
a
j
,
• the angle of rotation is equal to 180 degrees: a
i
a
j
,
• the angle of rotation is equal to 270 degrees: a
i
a
j
.
These two Boolean variables describe the angle of ro-
tation. Hence, we call this encoding cyclic Boolean
angle encoding. Figure 5 shows the assignment of the
Boolean variables for this encoding to elements of the
grids G
4,4
and G
5,5
.
The number of Boolean model variables of a
quadratic grid with an even number of m rows and
n = m columns for the angle encoding is equal to
m
2
/2 which is only 18
2
/2 = 162 for the grid G
18,18
.
The center element of a quadratic grid with an odd
number of m rows and n = m columns can be assigned
with each color due to the assumed cyclic reusable
coloring. Hence, this property must be taken into ac-
count for the setup of the model but no Boolean vari-
able is needed for the central grid element. The angle
encoding of a quadratic grid with an odd number of
rows and columns requires consequently (m
2
− 1)/2
which is only (17
2
− 1)/2 = 144 for the grid G
17,17
.
There are two more sources of improvementsorig-
inated from the cyclic Boolean angle encoding:
1. One of four rotated solutions be predefined by
fixed values of both Boolean variables of one of
the grid cells.
2. Tautologies of rectangle rules can be excluded
from the SAT-instance.
We developed a generator that creates .cnf -files
for cyclic SAT instances using the suggested cyclic
Boolean angle encoding. While the SAT-solver clasp-
2.0.0 needs 212,301.503 seconds for the calculation
of the first solution of a single cyclic reusable color
assignment expressed by 324 Boolean variables for
the grid G
18,18
, the same SAT-solver found the first
solution already after 98,140.862 seconds using the
cyclic Boolean angle encoding. This reduction of the
required runtime to 46.23 percent indicates both the
benefit of the cyclic Boolean angle encoding and the
unchanged extremely high complexity of the problem
itself.
5.2 Knowledge Transfer
Due to (3) there are 23,409 clauses for the grid G
18,18
.
Each clause describes a single rectangle condition. A
SAT-solver is able to remove tautology clauses or add
learned additional clauses. However, the SAT-solver
does not know properties of the problem which can be
utilized within the solution process.
We know, that the SAT-instance (the SAT formula
as . cnf file given to the SAT-solver) describes the
color patterns for a single color of a quadratic grid
which can be reused after a rotation by an angle of
k∗ 90
◦
,k = 1,2,3 for the other three colors. Based on
this knowledge we can conclude that four solutions of
the SAT-instance can be mapped to a unique pattern
applying a rotation by k ∗ 90
◦
. Because one of such
four solutions answers our purpose we can exclude
the rotated solutions by constant values of any pair of
variables which describe a quadruple. We transfer this
knowledge by adding clauses for a
1
= 0 and a
2
= 0.
In this way the number of free variables for the grid
G
18,18
is reduced from 162 to 160 and the number of
clauses is increased from 23,409 to 23,411.
The SAT-solver knows all these 23,411 clauses
but does not know their semantics. For that reason
the SAT-solver must take into account all remaining
2
160
≈ 1.46∗10
48
combinations of value assignments.
This large amount of combinations can be restricted
by a simple creative conclusion.
If we have a cyclic solution pattern of a quadratic
grid G
k,k
and remove both the first and the last row
and the left and the right column we get a cyclic so-
lution pattern of the quadratic grid G
k−2,k−2
. That
means it cannot create a correct cyclic color pattern
of a quadratic grid G
18,18
that includes an incorrect
pattern of a quadratic grid G
16,16
as center part.
Using the cyclic Boolean rectangle encoding the
grid G
18,18
needs 2 ∗ 17 = 34 additional Boolean
variables in comparison to the next central internal
grid G
16,16
. Hence, only a very small fraction of
the 2
160−34
≈ 8.5∗ 10
37
possible pattern for rotation-
frozen grids G
16,16
must be evaluated to find a correct
solution of the grid G
18,18
. The expansion step can be
solved in a very short period of time by a SAT-solver
again because only valid values of 34 Boolean vari-
ables must be found and many conflicts to the rectan-
gle rule exist.
In order to find all different cyclic rectangle-free
solutions of the grid G
18,18
we suggest the following
algorithm in which the knowledge about the cyclic
rectangle-free solutions for the grid G
16,16
is trans-
ferred to the SAT-instance of the larger grid G
18,18
.
1. Create a SAT-instance using the cyclic Boolean
encoding shown in Figure 5 (a) for the grid G
16,16
.
2. Frozen the rotation of the SAT-instance of step 1
by two clauses for a
1
= 0 and a
2
= 0.
3. Calculate all solutions of the SAT-instance of step
2.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
416

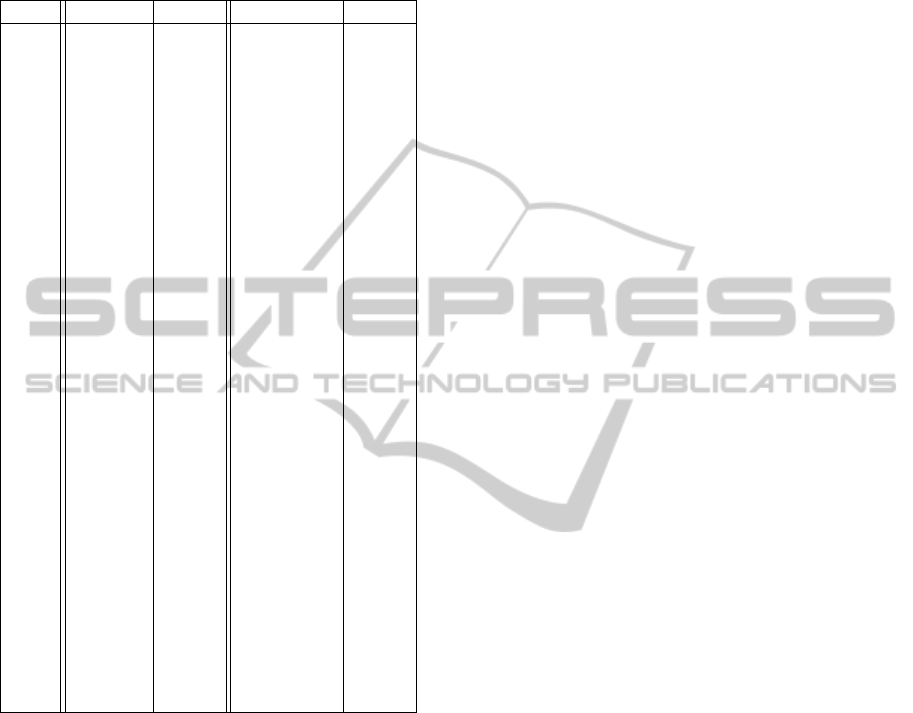
Table 3: Correct cyclic grids G
18,18
of different equivalence
classes extended by knowledge transfer from correct cyclic
grids G
16,16
calculated within a period of 60 days and the
results of the same experiment applied to the extension of
cyclic grids G
15,15
to cyclic grids G
17,17
.
days G
16,16
G
18,18
G
15,15
G
17,17
2 9,900 0 1,455,000 0
4 20,000 0 2,960,000 0
6 31,500 4 4,435,000 0
8 41,700 8 6,030,000 0
10 51,400 24 7,625,000 0
12 62,900 32 9,255,000 0
14 75,000 44 10,940,000 0
16 87,000 52 12,580,000 0
18 98,000 60 14,390,000 0
20 111,300 85 16,150,000 0
22 123,700 92 17,320,000 0
24 137,900 112 18,870,000 0
26 149,300 116 20,195,000 0
28 162,000 120 21,800,000 0
30 173,900 120 23,200,000 0
32 187,000 120 24,355,000 0
34 198,300 124 25,630,000 0
36 210,500 136 27,005,000 0
38 224,500 148 28,335,000 0
40 238,400 152 29,645,000 0
42 250,400 152 30,905,000 0
44 262,500 164 32,080,000 0
46 274,100 164 33,520,000 0
48 284,500 172 35,045,000 0
50 297,500 180 36,600,000 0
52 309,800 188 37,880,000 0
54 322,300 192 39,310,000 0
56 334,600 192 40,705,000 0
58 345,600 192 42,290,000 0
60 357,200 208 43,970,000 0
4. For each solution found in step 3 create a SAT-
instance based on the cyclic Boolean encoding
shown in Figure 5 (a) for the grid G
18,18
and ex-
tend this SAT-instance by constant clauses of one
solution found in step 3.
5. Solve the logically restricted SAT-instances which
were created in step 4.
We run an experiment over 60 days and found that
208 of 43,970,000 cyclic rectangle-free grids G
15,15
can be extended to cyclic rectangle-free grids G
17,17
.
The the last two columns of Table 3 show the details
of this experiment. It can be concluded that
Using a slightly changed knowledge transfer ap-
proach it can be verified whether this statement is true
for quadratic grids with an odd number of rows and
columns. We describe this adopted approach for the
most interesting case of the knowledge transfer from
the correct cyclic solution of the grid G
15,15
to check
for cyclic solutions of the grid G
17,17
.
1. Create a SAT-instance using the cyclic Boolean
encoding shown in Figure 5 (b) for the grid G
15,15
.
2. Frozen the rotation of the SAT-instance of step 1
by two clauses for a
3
= 0 and a
4
= 0 (the vari-
able a
1
and a
2
describe the center element, do not
contain rotation information, and must not be used
explicitly in the SAT-formula).
3. Calculate all solutions of the SAT-instance of step
2.
4. For each solution found in step 3 create a SAT-
instance based on the cyclic Boolean encoding
shown in Figure 5 (b) for the grid G
17,17
and ex-
tend this SAT-instance by constant clauses of one
solution found in step 3.
5. Solve the logically restricted SAT-instances which
were created in step 4.
We run a similar experiment again over 60 days
and found that none of 357,200 cyclic rectangle-free
grids G
16,16
can be extended to cyclic rectangle-free
grids G
18,18
. A conjecture of this experiment is that
no correct cyclic rectangle-free 4-coloring for the grid
G
17,17
exists. The rationale of this conjecture is that
the central element of the grid G
17,17
originates with
8 values 1 in the middle row and the middle column
fixed parts of possible rectangles which restrict the as-
signment of values 1 strongly. In the apparently more
complicated grid G
18,18
these values 1 can be chosen
within the quadruples such that no restriction com-
monly with the 1 value of the central four grid posi-
tions originates.
It should be mentionedthat the knowledge transfer
can be utilized recursively for all levels of a cascade
of quadratic grids of either an even number or an odd
number of rows and columns. The benefit in terms
of runtime depends on the ratio between the time to
solve the next smaller grid and the time for the trans-
fer of the knowledge .
6 COMPARATIVE STUDY
Many scientists all over the world tried to solve the
four-valued rectangle-free grid G
18,18
but all of them
failed due to the extreme complexity of the problem.
For that reason we cannot compare our results with
solutions of other scientists but must refer to our own
solutions.
The description of the significantly simpler prob-
lem of the grid G
17,17
on the web page (Fortnow and
Gasarch, 2009) and more than 150 comments about
ArtificialIntelligenceandCreativity-TwoRequirementstoSolveanExtremelyComplexColoringProblem
417

failed approaches in the period of time from 2009
to 2012 confirm our scientific progress. In Febru-
ary 2012 we published our found solution for the grid
G
17,17
on the web page (Fortnow and Gasarch, 2012)
and announced that we solved even the extremely
more complex grid G
18,18
. At this time our paper
(Steinbach and Posthoff, 2012a) about the solution of
the G
18,18
was accepted.
In this ICAART-2013 paper we suggested two ad-
vanced creative approaches and reached the following
improvements.
1. The reduced cyclic Boolean angle encoding al-
lows to solve the four-valued rectangle-free grid
G
18,18
using only 162 Boolean variables and re-
duces the required runtime to 46.23 percent.
2. Using the approach of the knowledge transfer we
found 256 four-valued rectangle-free grid G
18,18
of different equivalence classes within 71 days,
which reduces the average runtime for each of
these solutions to 11.29 percent.
7 CONCLUSIONS
We explored in this paper the so far unsolved problem
whether the grids G
17,17
, G
17,18
, G
18,17
, and G
18,18
are
rectangle-free 4-colorable. Our study has shown that
the fraction of 4-colorable grids of the size 18 × 18
is extremely small. Hence, finding a rectangle-free
4-colored grid G
18,18
out of the unimaginably large
number of 1.16798∗ 10
195
of all possible assignments
of 4 colors is significantly more difficult than detect-
ing a single electron within the whole universe and
requires both AI and creativity.
Our suggested advanced approaches for strong
complex problems are:
• the utilization of problem specific constraints by a
fitting special encoding,
• the knowledge transfer from simpler subtasks in
order to restrict the remaining search space.
In the special case of the explored edge coloring
our suggested cyclic Boolean angle encoding allows
to reduce the number of Boolean variables again to
one half from 324 to 162 for the grid G
18,18
which
basically has required a model of 648 Boolean vari-
ables. For the same application the knowledge trans-
fer from subtasks reduces the effort to solve the next
more complex task strongly.
REFERENCES
Biere, A. (2010). Lingeling, plingeling, picosat and pre-
cosat at sat race 2010. Technical Report 10/1, Institute
for Formal Models and Verification, Johannes Kepler
University, Linz, Austria.
Fenner, S., Gasarch, W., Glover, C., and Purewal, S.
(2009). Rectangle free coloring of grids. http://
www.cs.umd.edu/∼gasarch/papers/grid.pdf.
Fortnow, L. and Gasarch, B. (2012). Computational com-
plexity - the 17x17 problem solved! (also 18x18).
http://blog.computationalcomplexity.org/ 2012/ 02/
17x17-problem-solved-also-18x18.html.
Fortnow, L. and Gasarch, W. (2009). Rectangle free col-
oring of grids. http://blog.computationalcomplex-
ity.org/ 2009/ 11/ 17x17-challenge-worth-28900-this-
is-not.html.
Gebser, M., Kaufmann, B., Neumann, A., and Schaub, T.
(2007). Logic Programming and Nonmonotonic Rea-
soning, chapter clasp: A Conflict-Driven Answer Set
Solver, pages 260–265. Springer, Berlin, Heidelberg.
Marx, D. (2004). Graph colouring problems and their appli-
cations in scheduling. Periodica Polytechnica, Elec-
trical Engineering, 48(1):11–16.
Posthoff, C. and Steinbach, B. (2004). Logic Functions
and Equations - Binary Models for Computer Science.
Springer, Dordrecht, The Netherlands.
Steinbach, B. and Posthoff, C. (2009). Logic Functions and
Equations - Examples and Exercises. Springer Sci-
ence + Business Media B.V.
Steinbach, B. and Posthoff, C. (2012a). Extremely com-
plex 4-colored rectangle-free grids: Solution of open
multiple-valued problems. In Proceedings of the IEEE
42nd International Symposium on Multiple-Valued
Logic (ISMVL 2012), pages 37–44, Victoria, British
Columbia, Canada.
Steinbach, B. and Posthoff, C. (2012b). Utilization of
permutation classes for solving extreme complex 4-
colorable rectangle-free grids. In The 2012 Interna-
tional Conference on Systems and Informatics (ICSAI
2012), pages 2361–2370, Yantai, China.
Steinbach, B., Posthoff, C., and Wessely, W. (2010). Ap-
proaches to shift the complexity limitations of boolean
problems. In Computer - Aided Design of Discrete
Devices - CAD DD 2010, Proceedings of the Seventh
International Conference, pages 84–91, Minsk, Be-
larus.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
418