
A Linearization Approach for Project Selection with
Interdependencies in Resource Costs
Ali Shafahi and Ali Haghani
Department of Civil & Environmental Engineering, University of Maryland,
1173 Glenn L. Martin Hall, College Park, MD 20742, U.S.A.
Keywords: Project Management, Project Selection, Learning Curve, Interdependencies, MIP, Nonlinear, Quadratic,
Linearization.
Abstract: In this paper a new formulation is proposed for project selection problem which considers project
interdependencies. Project interdependencies are factored in using the learning curve concept. The problem
is modeled as a Mixed Integer Program (MIP) with quadratic constraints. To solve the problem the
quadratic constraints are linearized using a new method proposed in this paper and the benefits of this
approach compared to the conventional methods are emphasized. The application of this methodology is
illustrated using a numerical example. The result shows the superiority of this method in reducing the
number of variables dramatically.
1 INTRODUCTION
The project selection problem which is selecting a
good set of projects to be executed from a pool of
available projects is a very important decision for
managers and decision makers. The goal of this
selection is to maximize the overall profit. The main
reason for the limitation in the number of selected
projects is resource availability. In nature, this
problem is similar to the knapsack problem.
Sometimes the project selection problem is referred
as project portfolio selection. This nomenclature is
used to emphasis the importance of looking at the
entire portfolio of the projects rather than each
project individually. Looking at each project
individually will not result in the best portfolio
because projects are not usually independent of each
other.
The structure of this paper is as follows. A brief
review of the project selection problem and the
related literature is given in section 2. Section 3
defines the problem. The solution method is
provided in section 4. Finally, the last two sections
illustrate an example of how the model is solved
using the methodology offered and the conclusions
are made.
2 LITERATURE REVIEW
While a few of previous articles which have focused
on project portfolio selection have the assumption of
project independency, it has been argued that when
the goal of the decision is to optimize the entire
portfolio of projects, project interdependencies are
important.
The interdependencies and interactions among
projects mainly fall into three different categories,
namely: benefit, cost, and outcome. The benefit
category refers to an increase in profit of a given
project as a result of doing another project which is
related (dependent) to that project. The Outcome
category refers to the increase in the probability of
success of a given project if an earlier project which
is in the same category is completed. Finally, the
cost category refers to the decrease in costs and all
other resources which a given project is consuming
if an earlier project of that kind is completed.
These interdependencies among projects have
been addressed in previous research (Killen and
Kjaer, 2012) (Liesio et al., 2008) (Bhattacharyya et
al., 2011).
The project selection and decision making
problems which consider interdependencies have
been dealt with using different solution techniques.
Some have used goal programming (Santhanam and
82
Shafahi A. and Haghani A..
A Linearization Approach for Project Selection with Interdependencies in Resource Costs .
DOI: 10.5220/0004214402300235
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 230-235
ISBN: 978-989-8565-40-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)
Kyparisis, 1995) (Lee and Kim, 2000), while others
have approached the problem with linear
programming, branch and bound, or using heuristic
approaches (Iniestra and Gutierrez, 2009) (Schmidt,
1993) (Carazo, et al., 2010). Constraint
Programming is also another approach used for
solving problems of this type (Liu and Wang, 2011).
When interdependencies are inserted in
mathematical Operation Research models, models
become nonlinear. Linearization techniques are used
to convert the nonlinear problem into linear. The
linearization approach used in a majority of research
including (Snthanam and Kyparisis, 1996) is based
on the approach introduced by (Glover and
Woolsey, 1974). Based on that approach,
polynomial binary problems can be reduced to linear
problems. This reduction is facilitated by
introducing a new variable for each non-linear term
and bounding those new variables using a set of
constraints. While this approach can be applied to
linearize many binary problems, it requires the
addition of many new variables.
This paper contributes to the project selection
problem by providing a formulation to the problem
and introducing a method to linearize the project
selection problem which can potentially decrease the
number of new required variables.
3 PROBLEM DESCRIPTION
The project selection problem is a planning problem.
However since the inputs are uncertain and are
subjected to change in different times, the problem is
solved at different times when a new input is
inserted in the model. A new input could be, for
example, the availability of a new project in the
project pool.
3.1 Interdependency Modeling
As mentioned earlier, the interactions among
projects mainly fall into one of the benefit, outcome,
or cost categories. The main focus of this research is
on the cost interactions which will lead to a decrease
in required resources. This decrease might be
because of several reasons, some of which are: (1)
Learning curves: The famous effect which usually
happens when the work is more labor intensive than
automated. An extensive definition and analysis of
different learning curves are provided in (Anzanello
and Fogliatto, 2011). (2) Labor efficiency. (3)
Purchase of new equipment: The decrease in the
resource requirement of the later projects due to
purchase of equipment for prior projects.
Clearly the main interdependencies are between
projects which fall into a similar category. In this
research it is assumed that projects which have
interdependencies are from the same categories. For
instance doing a number of related planning projects
might lead to a decrease in the resources required for
a later planning project.. However doing a planning
project will not decrease the resources required for a
construction project at a later time.
When the number of completed projects is
known, using the shape of the learning curve, the
updated number of resources can be derived. This
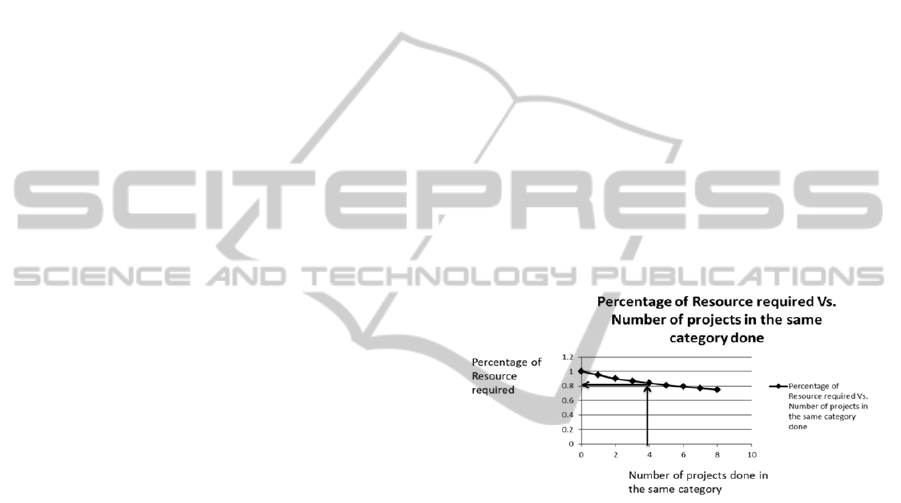
attribute is shown in Figure 1. As it is illustrated in
Figure 1, as the number of projects completed
increases, the resource requirements for later
projects which are from the same category
decreases. Usually, this decrease is more for the first
projects and then the rate of decrease decreases until
it meets a certain amount of resource (similar to a
learning curve).
Figure 1: decrease in resource requirements due to
previous projects completed.
To further illustrate how these project
interactions are modeled, assume that projects A, B,
and C are all design projects which fall into the same
category. For instance, they are 3 similar IT
development modules. Also consider that time-wise
they are planned to be done sequentially (i.e. project
B’s planned start time is after completion of Project
A, and project C’s is after project B). The resources
required for executing just one of A, B, and C is
350, 400, and 450 man-hours respectively. However
if project A is selected for execution, project B will
require 90% of its original resources (360 man-
hours). If either of the projects of A or B is selected
and executed, project C will require 90% of its
original estimation (405 man-hours). And if both
projects A and B are executed, project C will require
only 85% percent of its original estimate (382.5
man-hours).
ALinearizationApproachforProjectSelectionwithInterdependenciesinResourceCosts
83

3.2 Resource Type
The resources considered in this research are
renewable resources. A renewable resource will not
be available when it is being used in a project for the
duration of the project. After the project is done, the
resources will be added again to the resource pool.
Human resources are a sample of renewable
resources. Due to the characteristics of renewable
resources, time attributes of projects such as
duration and starting time become important in
project selection.
3.3 Formulation
The model formulation for the project selection
problem is similar to a knapsack problem and is as
follows:
∑
(1)
St.
,
∑
:
∀,
(2)
,
∑
,,
∀,
(3)
,
∑∑
,,
,
,,
∀,
(4)
∑
,,
1∀,
(5)
,
∑
,
:∈
,
∀,
(6)
,
,,
∈
0,1
∀,
,,
(7)
Where:
: profit of project “i",
: a binary variable which is equal to 1 if
project “i" is selected for execution and it is
equal to 0 otherwise,
,
: an auxiliary integer variable which
measures the number of selected projects
which are from category “CAT” and will be
finished up to time “T”,
,
: amount of type “type” resources
project “i" will consume if selected for
execution. (continuous auxiliary variable),
,,
: an auxiliary binary variable which
is used for the piecewise linear function,
: the available amount of resources
of type “type” at each time,
,,
: is a 3 dimensional parameter
vector which indicates the number of
resources type “type” which are required
for project “i" if scenario “j” has occurred.
Scenario “j” indicates how many projects
have been completed up to the time project
“i" is going to start,
,
: a parameter matrix which indicates
that project “i" is within what category,
: The time project “i" is going to
start if selected for execution, and
: The time project “i" will be
completely executed if selected for
execution.
Constraints (2) through (5) are constraints which
are used for determining how many resources are
required for project “i", if selected. They are
representative of the piecewise linear function of the
learning curve. Constraints (6) are the resource
limitation constraints for each time, “T”, and each
resource type.
4 SOLUTION METHOD
In the following subsections a method to linearize
constraints (5) is proposed.
4.1 Linearizing the Quadratic
Constraints
To linearize the quadratic constraints (6), a new set
of continuous variables and constraints are
introduced. Each quadratic term (
,
) is
replaced with a new continuous variable (
,
) and
constraints (8), (9) and (10) are added to the
problem. Using the new variable, constraints (6) are
rewritten as (11):
,
(8)
,
,
(9)
,
,,
(10)
∑
,:∈
,
∀,
(11)
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
84

Where,
,
is an auxiliary continuous variable
which indicates the amount of resource project “i"
will consume. If project “i" is selected this variable
should get a value equal to
,
and if not its
value should be equal to 0.
,,
is the
minimum amount of resources each project will
consume.
Constraints (8) are enforcing
,
to be equal
to zero if project “i" is not selected. Constraints (9)
are enforcing
,
to have a cap equal to
,
.
Constraints (10) are also introduced so that
,
will be given a positive value when it’s respective
project, “i", is selected.
These constraints on their own do not encourage
,
to be set at its true value. To overcome this
difficulty
,
is incentivized in the objective
function. The updated objective function is:
∑
∑∑
,
(12)
Where, M is an incentivizing (penalty) factor.
4.2 Finding a Suitable Incentivizing
Value, M
Finding an appropriate value for the incentivizing
factor, M, is very important since this is directly
related to finding a desirable solution. If M is set to
be too low, the solutions derived from solving the
optimization problem will not necessarily be a
feasible solution to the main problem. i.e. there at-
least exists a resource variable (
,
) for which all
three of the following conditions hold:
,
,
;
,
,
;
,
0
(13)
Since the solution resulted from this value of M
is not feasible and is resulted from a relaxation, it
can act as an upper bound to the problem. The
relaxed constraint in this case is:
,
,
.
If the incentive (Penalty) is too high, the nature
of the problem is changed. In this new problem, the
optimization model tries to maximize the resources
consumed (
,
). The solution to this problem will
not necessarily be optimal to the main problem.
However since all of the constraints are forced to be
holding (including
,
,
) and no constraint is
violated, the solution will be feasible to the main
problem. This solution could act as a lower bound
(feasible solution).
Based on these facts about the incentive’s value,
the algorithm proposed for finding the solution is as
follows:
• Step 1- Pick a reasonable Value for the
incentive (penalty) and solve the linear MIP
model.
• Step 2- Do solution check, i.e., check all
values of
,
which have a value greater
than 0 and also calculate the main objective
function (MainObj) which does not include
the penalty term. If at-least one positive
value of
,
’s is not equal to
,
, go to
step 4.
• Step 3- The solution found from step 2 is a
feasible solution and can act as a lower
bound. If stopping criteria is not met,
decrease the incentive’s value and go to
step 2.
• Step 4- The solution found from step 2 is a
solution for the relaxed problem. It is as an
upper bound to the main problem. If
stopping criteria is not met, increase the
incentive’s value and go to step 2.
The stopping criteria could be either the gap
between the upper bound and lower bound is
acceptable or there is no gap and the solution is
optimal.
This algorithm has the potential to reduce the
number of required additional variables and hence
improve the solution time.
As mentioned in the literature review section,
(Glover & Woolsey, 1974)’s method has been used
for linearizing nonlinear polynomial binary
problems in previous works. To demonstrate the
power of our method in reducing the number of
variables, Glover’s method is applied to the
proposed model in this paper and the two methods
are compared based on the number of additional
variables required for linearization.
To apply Glover’s method to the model
presented in this paper,
,
in constraint (5)
should be replaced with its equivalent value stated in
the right hand side of constraint (3). Then each 0-1
quadratic term (
,,
) should be replaced
with a new variable (
,,,,
). This means
|
|
|
|
|
|
|
|
|
|
new variables
should be added to this problem. However since
constraint (3) is no longer needed and the
,
variables are omitted from the problem,
|
|
|
|
variables are diminished. Thus the net additional
ALinearizationApproachforProjectSelectionwithInterdependenciesinResourceCosts
85

variables needed in this case are:
|
|
|
|
|
|
|
|
|
|
1).
Based on the method provided in this paper, only
|
|
|
|
new variables should be added.
Therefore, the approach provided in this paper
reduces the number of variables by 1
1
|
|
|
|
|
|
1
100%. To illustrate this
benefit, assume that the projects fall into 3
categories (CAT=3), and the last project considered
in this planning horizon is planned to start at time
T=6, and at most 10 projects are available for any of
the categories. In this not so large example, the
number of new variables needed for modeling this
problem is 1
1
10361
100% =
99.44% less than the Glover method.
5 A NUMERICAL EXAMPLE
To illustrate how this method and algorithm works, a
pool of projects was generated. This pool contained
30 projects, each consuming 5 different types of
resources. Each of these 30 projects was randomly
assigned to one of three categories. The attributes of
the learning curve have been summarized in Table 1.
The availability of resource types 1 through 5 were
assumed to be 5, 7, 4, 6, and 5 units respectively.
The summary of the procedure to find the
optimum solution is provided in Table 2. In this
table, the ObjFunc column contains the value of the
objective function with the incentive, and the
MainObj column contains the objective function
value of the main problem. The optimal solution is
found after 4 iterations. The solution is proven to be
optimal because the upper bound and the lower
bound (feasible solution) of the main objective
function have converged and are equal. The operator
of this model could’ve stopped the model at step 3
since the gap between the upper bound and the lower
bound is at most 0.5%.
Step 5 has been added to illustrate the change in
the nature of the problem when the penalty factor is
too high. In this case, the number of projects
selected is big, but they are not the most profitable
set of projects. They are the projects which together
consume the most resources.
6 CONCLUSIONS
A model was introduced to deal with the project
selection problem when cost interdependencies
among projects exist. A new method to linearize the
quadratic constraints of this problem was introduced.
And based on this method an algorithm is offered to
solve the problem. It is shown that this method
reduces the number of variables in the linearization
procedure compared to previous works in this area
which is based on the Glover’s method.
This research has had contributions in both
modeling and methodology. However, there are
several different avenues for future work. In the
modeling part, other types of interdependencies can
be added to build a more comprehensive model.
Also, the assumption of certainty which is implied in
this model can be relaxed and a model which
considers the probable variations in costs can be
developed. As for the methodology, this method of
linearization can be applied to other problems.
REFERENCES
Anzanello, M. J. and Fogliatto, F. S. (2011). Learning
curve models and applications: Literature review and
research directions. International Journal of Industrial
Ergonomics, 573-483.
Bhattacharyya, R., Kumar, P. and Kar, S. (2011). Fuzzy
R&D portfolio selection of interdependent projects.
Computers & Mathematics with Applications, 3857-
3870.
Carazo, A. F., Gomez, T., Molina, J., Hernandez-Diaz, A.,
Guerrero, F. and Caballero, R. (2010). Solving a
Comperehensive model for Multi-Objective Project
Selection . Computers and Operational Research,
630-639.
Glover, F. and Woolsey, E. (1974). Converting the 0–1
polynomial programming problem to a 0–1 linear
problem. Operations Research, 180-182.
Iniestra, J. G. and Gutierrez, J. G. (2009). Multicriteria
decisions on interdeendent infrastructure
transportation projects using an evolutionary-based
framework. Applied Soft Computing, 512-526.
Killen, C. P. and Kjaer, C. (2012). Understanding project
interdependencies: The role of visual representation,
culture and process. International Journal of Project
Management, 554-566.
Lee, J. W. and Kim, S. H. (2000). Using analytical
network process and goal programming for
interdependent information system project selection.
Computers & Operations Research, 367-382.
Liesio, J., Mild, P. and Salo, A. (2008). Robust portfolio
modeling with incomplete cost information and
project interdependencies. European Journal of
Operaional Research, 679-695.
Liu, S.-S. and Wang, C.-J. (2011). Optimizing project
selection and scheduling problems with time-
dependent resource constraints. Automation in
Construction, 1110-1119.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
86

Santhanam, R. and Kyparisis, J. (1995). A multiple criteria
decision model for information system project
selection. Computers & Operations Research, 807-
818.
Schmidt, R. L. (1993). A Model for R and D Project
Selection with Combined Benefit, Outcome and
Resource Interactions. IEEE TRANSACTIONS ON
ENGINEERING MANAGEMENT, 403-410.
Snthanam, R. and Kyparisis, G. J. (1996). A decision
model for interdependent information system project
selection. European Journal of Operational Research,
380-399.
APPENDIX
Table 1: Learning curve attributes.
Number of projects
done in the
category
Resource Requirement
(Percentage of original
estimation)
Number of
projects done in
the category
Resource Requirement
(Percentage of original
estimation)
0 100%
6 78%
1 90%
7 76%
2 85%
8 75%
3 83%
9 75%
4 81%
10 75%
5 80%
Table 2: Model and algorithm results.
Itera
tion
M
Infeasibility
(Violation)
ObjFunc MainObj
# of
projects
selected
Upper
Bound
(Feas. Sol)
running
time (s)
1 20 yes 274246.76 272493.22 14 272493.22 0.42
2 100 yes 281260.95 272493.22 14 272493.22 0.42
3 500 no 318955.89 270874.28 15 (270874.28) 0.53
4 300 yes 299723.25 270874.28 15 270874.28 0.43
5 10000 no 1335010.1 220459.88 16 (220459.88) 1.34
ALinearizationApproachforProjectSelectionwithInterdependenciesinResourceCosts
87
