
Desirability Function Approach on the Optimization
of Multiple Bernoulli-distributed Response
Frederick Kin Hing Phoa and Hsiu-Wen Chen
Institute of Statistical Science, Academia Sinica, 128 Academia Rd. Sec. 2, Nangang Dist., Taipei 115, Taiwan
Keywords:
Multiple Response Optimization, Desirability Function, Bernoulli-distributed Responses, Logistic Regression.
Abstract:
The multiple response optimization (MRO) problem is commonly found in industry and many other scientific
areas. During the optimization stage, the desirability function method, first proposed by Harrington (1965),
has been widely used for optimizing multiple responses simultaneously. However, the formulation of tradi-
tional desirability functions breaks down when the responses are Bernoulli-distributed. This paper proposes
a simple solution to avoid this breakdown. Instead of the original binary responses, their probabilities of de-
fined outcomes are considered in the logistic regression models and they are transformed into the desirability
functions. An example is used for demonstration.
1 INTRODUCTION
As science and technology have advanced to a higher
level nowadays, investigators are becoming more in-
terested in and capable of studying large-scale sys-
tems. In industry, engineering and many other ar-
eas of science, data collected often contain several re-
sponses of interest for a single set of explanatory vari-
ables. There are plenty of model selection methods,
like the LASSO (Tibshirani, 1996), Dantzig selec-
tor (Candes and Tao 2006; Phoa et al., 2009), SRRS
(Phoa, 2012ab) and so on, to find a setting of the ex-
planatory variables that optimizes a single response.
However, when multiple responses are required to
be optimized simultaneously, it is usually difficult to
come up with an optimal setting, or even several fea-
sible settings, of explanatory variables.
Multiple response problems (Khuri, 1996; Kim
and Lin, 2006) consists of three stages: data collec-
tion (design of experiments), model building, and op-
timization, specifically called multiple response op-
timization (MRO). There exists several popular ap-
proaches to reduce multiple responses to one with a
single aggregated measure and solves it as a single
objective optimization problem. They include the de-
sirability function (Harrington, 1965; Derringer and
Suich, 1980; Kim and Lin, 2000), the generalized dis-
tance measure method (Khuri and Conlon, 1981), a
square error loss function (Pignatiello, 1993; Vining,
1998), a goal attainment approach (Xu et al., 2004),
and so on.
Simple linear regression is often used to investigate
the relationship between a single explanatory vari-
able and a single response, but often the response is
not a numerical value. Instead, the response is sim-
ply a designation of one of two possible outcomes,
e.g. yes or no, accept or decline, etc. In fact, data
involving the relationship between explanatory vari-
ables and Bernoulli-distributed responses abound in
just about every discipline from engineering to, the
natural sciences, medicine, education, etc. Thus, it
becomes a challenge to deal with the optimization of
multiple responses such that these responses are bi-
nary.
The goal of this paper is to propose a modified
method to the Harrington’s desirability function ap-
proach to adapt with the optimization of multiple
Bernoulli-distributed responses. In section 2, the Har-
rington’s desirability function is introduced and a dis-
cussion is included on how the formulation is broken
down when binary responses are dealt. In section 3,
a modified method is proposed on the model building
procedure prior to the desirability function, and the
formulation becomes more simplified. Section 4 pro-
vides an example to demonstrate how the proposed
method works, and some concluding remarks are in-
cluded in the last section.
127
Kin Hing Phoa F. and Chen H. (2013).
Desirability Function Approach on the Optimization of Multiple Bernoulli-distributed Response.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 127-131
DOI: 10.5220/0004216701270131
Copyright
c
SciTePress

2 THE DESIRABILITY
FUNCTION AND ITS
LIMITATION TO
BINARY RESPONSES
The desirability function method transforms each re-
sponse into a dimensionless individual desirability
scale and then combines these individual desirabil-
ities into one whole desirability using a geometric
mean. Generally speaking, when an experimental
result with m responses y = (y
1
,...,y
m
) and k fac-
tors x = (x
1
,...,x
k
) is given, m models can be built
for each response using a common model selection
approach, and this leads to m fitted responses ˆy =
( ˆy
1
,..., ˆy
m
). Then each fitted response ˆy
i
is trans-
formed into an individual desirability value d
i
, 0 ≤
d
i
≤ 1. The overall desirability, denoted by D, is
the geometric mean of all the transformed responses,
given by
D = (d
1
× ··· × d
m
)
1/m
The value of d
i
increases as the desirability of the
corresponding response increases. The single value
of D gives the overall assessment on how desirable is
the combined m responses under the given setting of
k explanatory variables. If D is very close to 0, which
means one or more indiviual desirabilities is close to
0, then the corresponding setting would not be accept-
able. On the other hands, if D is close to 1, then all of
the individual desirabilities are simultaneously close
to 1, thus the corresponding setting would be a good
compromise among the m responses. The optimiza-
tion goal in this method is to find the maximum of
the overall desirabilities D and its associated optimal
setting of explanatory variables.
The transformation from ˆy
i
to d
i
can be either one-
sided or two-sided. One-sided transformations are
used when the goal is to either maximize or mini-
mize the response, while two-sided transformations
are used when the goal is for the response to achieve
some specified target value. Harrington (1965) used
exponential functions to transform ˆy
i
to d
i
, specifi-
cally d
i
= exp(−exp(−ˆy
i
)) for a one-side transfor-
mation and d
i
= exp(−∥ˆy
i
∥
r
) for a two-sided trans-
formation, where r is a user-selected shape parameter
that should be carefully chosen to reflect expert opin-
ion. Derringer and Suich (1980) modified Harring-
ton’s transformations and classified them into three
forms. When the goal is to maximize the i
th
response,
the individual desirability is given by the one-sided
transformation
d
i
=
0, ˆy
i
(x) < L
(
ˆy
i
−L
U−L
)
r
, L ≤ ˆy
i
≤ U
1, ˆy
i
(x) > U
where U and L are acceptable maximum and mini-
mum values of the response y
i
respectively, and r is a
user-specified weight describing the shape of the de-
sirability function. Similarly, to minimize the i
th
re-
sponse, the individual desirability is given by the one-
sided transformation
d
i
=
1, ˆy
i
(x) < L
(
U−ˆy
i
U−L
)
r
, L ≤ ˆy
i
≤ U
0, ˆy
i
(x) > U
When the goal is to obtain a target value, the individ-
ual desirability is given by the two-sided transforma-
tion
d
i
=
0, ˆy
i
(x) < L
(
ˆy
i
−L
T −L
)
r
1
, L ≤ ˆy
i
≤ T
(
U−ˆy
i
U−T
)
r
2
, T ≤ ˆy
i
≤ U
0, ˆy
i
(x) > U
where T is the target value of the response y
i
, r
1
and
r
2
are user-specified weights describing the shapes
of two-sided desirability function. Derringer (1994)
propose an extended an general form of D, using a
weighted geometric mean, given by
D = (d
w
1
1
,...,d
w
m
m
)
1/
∑
i
w
i
where w
i
is the i
th
weight on the i
th
response specified
by users.
The desirability function approach works fine
when the responses are continuous. However, when
the responses are Bernoulli-distributed, the ordinary
regression model does not provide meaningful fitted
responses. Let’s consider a simple example. Given a
binary response y
1
where +1 and −1 correspond to
YES and NO respectively, and let a setting of x re-
turn a fitted value ˆy
1
= 0.8 through a linear regression
model. If the goal is to maximize the response, fol-
lowing the traditional desirability function approach,
a upper and a lower bound of y
1
has to be found prior
to the transformation of d
1
from y
1
under a setting of
x. Let’s say the upper bound U = 0.9 and the lower
bound L = 0.5 in the fitted response ˆy
1
, and set r = 1,
then d
1
= (0.8 − 0.5)/(0.9 − 0.5) = 0.75. Although
it is mathematically possible to compute the individ-
ual desirability d
1
, it is very difficult to interpret its
meaning because neither ˆy
1
, U nor L carry any mean-
ings that correspond to YES or NO, and thus the arith-
metics among them seem not meaningful. Therefore,
instead of modeling the response via ordinary linear
regression, the logistic regression is suggested in the
next section.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
128

3 A PROPOSED METHOD
FOR MULTIPLE
BERNOULLI-DISTRIBUTED
RESPONSES
Unlike ordinary linear regression, logistic regression
is a type of regression analysis used for predicting
binary outcomes or Bernoulli trials rather than con-
tinuous outcomes. Given this difference, the logistic
regression take the natural logarithm of the odds to
create a continuous criterion. Mathematically speak-
ing,
log
π
1 − π
=
∑
i
β
i
x
i
where the term in the left side is called the logit (nat-
ural logarithm of the odds). Notice that the unintu-
itive logit needs to be converted back to the odds via
the exponential function. Therefore, although the ob-
served variables in logistic regression are discrete, the
predicted scores (logit) are modeled as a continuous
variable. Notice that π and 1 − π are the probabilities
that the outcomes are +1 and −1 respectively.
By some simple algebra, the fitted probability π
(the outcome is +1) can be rewritten as
π(x) =
1
1 + e
−
∑
i
β
i
x
i
Since these fitted probabilities are continuous, they
can serve as the substitutions of the Bernoulli-
distributed responses to transform into the desirabil-
ity function. In general, the proposed method follows
the steps below. Given an experimental result that
consists of k continuous factors x and m Bernoulli-
distributed responses y,
1. Fit m logistic regression models with x
1
,...,x
k
and the corresponding estimates β
1
,...,β
k
are ob-
tained, where β
i
is a vector of length m.
2. For each setting of x in a trial, obtain m fitted prob-
abilities π
1
,...,π
m
.
3. Transform the fitted probabilities π
1
,...,π
m
into
individual desirability function d
1
,...,d
m
.
4. Obtain the overall desirability function D, which
is the geometric mean of the individual desirabil-
ity functions.
Due to the nature of the fitted probabilities, the
optimization goal is to either maximize or minimize
π. When the goal is to maximize the i
th
π, in other
words, to maximize the probability of i
th
response as
+1 (with a defined meaning like YES or accepted),
the individual desirabilities is given by
d
i
=
0,
ˆ
π
i
(x) < L
(
ˆ
π
i
−L
U−L
)
r
, L ≤
ˆ
π
i
≤ U
1,
ˆ
π
i
(x) > U
where U and L are acceptable maximum and mini-
mum probabilities that i
th
response as +1, and r is
a user-specified weight. It is obvious that U ≤ 1 and
L ≥ 0. If both equalities hold, the individual desirabil-
ity function can be simplified as d
i
=
ˆ
π
i
, or simply the
probability of i
th
response as +1. Similarly, when the
goal is to minimize the i
th
π, in other words, to min-
imize the probability of i
th
response as +1, or equiv-
alently, to maximize the probability of i
th
response as
−1 (with a defined meaning like NO or rejected), the
individual desirabilities is given by
d
i
=
1,
ˆ
π
i
(x) < L
(
U−
ˆ
π
i
U−L
)
r
, L ≤
ˆ
π
i
≤ U
0,
ˆ
π
i
(x) > U
It is obvious again that U ≤ 1 and L ≥ 0. If both equal-
ities hold, the individual desirability function can be
simplified as d
i
= 1 −
ˆ
π
i
, or simply the probability of
i
th
response as −1. Notice that it is not necessary to
define the two-sided transformation because a target
value T in between 0 and 1 is meaningless to the op-
timization process in Bernoulli-distributed responses.
For example, if a target value T = 0.4 is desired for a
particular response, it means the optimized response
is a linear combination of both +1 and −1 with some
weights. This violates the nature of the response that
there are only two possible choices (+1 and −1).
4 AN ILLUSTRATIVE EXAMPLE
Vander Heyden et al., (1999) used the high-
performance liquid chromatography (HPLC) method
to study the assay of ridogrel and its related com-
pounds in ridogrel oral film-coated tablet simulations.
They chose to use a 12-run Plackett-Burman design to
identify the importance of eight factors on seven re-
sponses. We consider only two out of seven specific
responses, which are the percentage recovery of rido-
grel (%MC) and analysis time (t
R
). Both responses
are continuous variables. The Stepwise Response Re-
finement Screener (SRRS) proposed by Phoa (2012a)
identifies that Factors E and F (the percentage organic
solvent in the mobile phase at the start and at the end
of the gradient) have significant impact to %MC, and
Factors B (Column Manufacturer) and F have signifi-
cant impact to t
R
. The ordinary linear regression mod-
els of %MC and t
R
have p-values less than 0.0005.
DesirabilityFunctionApproachontheOptimizationofMultipleBernoulli-distributedResponse
129
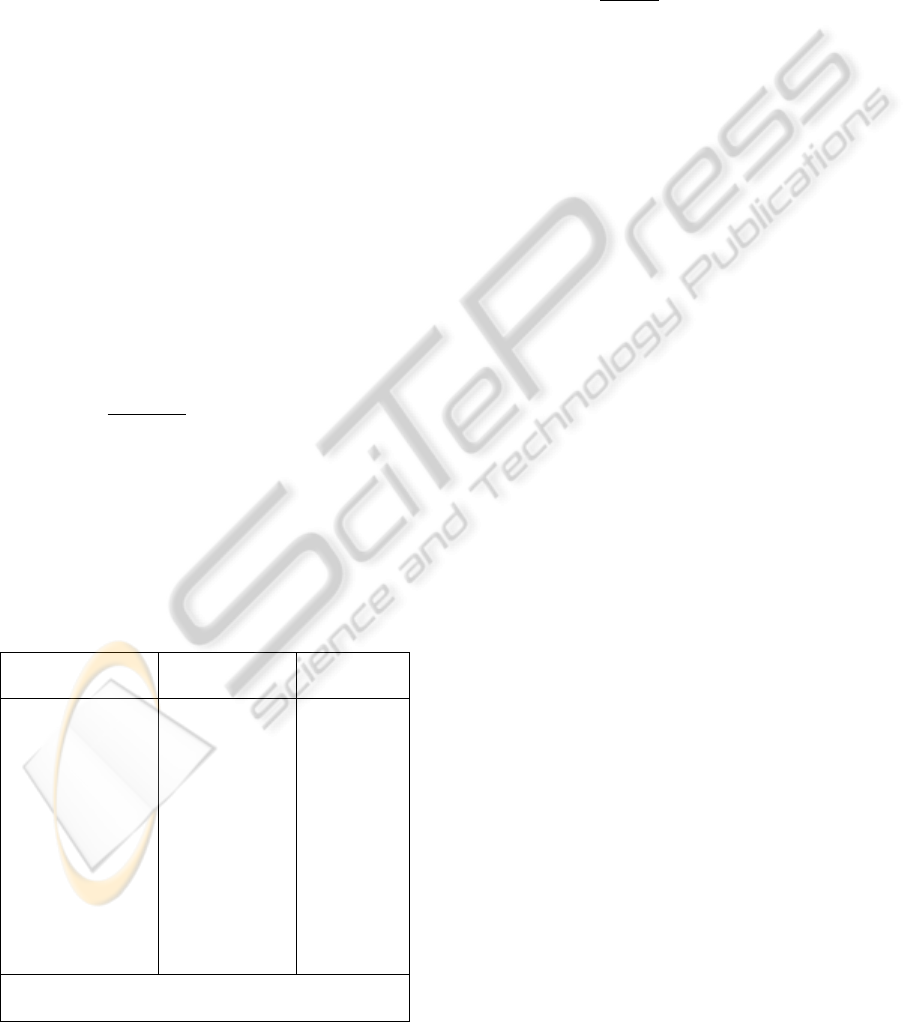
Table 1 gives three factors, design matrix and the
observed two responses. There are two forms of ob-
served responses: continuous and binary. The con-
tinuous responses are the original data from Vander
Heyden et al. (1999). However, this example aims at
demonstrating the proposed method to deal with mul-
tiple response problem, so the responses are modified
into binary. In specific, the +1 label in both binary re-
sponses represent the original observed responses that
are higher than their nominal values, and the −1 label
represent the opposite. The logistic regression models
for these two responses are
ˆ
π(%MC) = 1/(1 + e
−(2.4167−0.3333B−0.5000E+0.2500F)
)
ˆ
π(t
R
) = 1/(1 + e
−(15.1667+1.3333B−0.3333E−0.1667F)
)
where B is an indicator variable such that it is 1 if the
column manufacturer is Prodigy, and 0 otherwise.
To obtain upper and lower bounds of
ˆ
π(%MC),
its logistic regression model is used on the setting of
explanatory variables given in the data. Among 12
predicted responses, the maximum and minimum of
them are 0.7914 and 0.3393 respectively. It is obvious
that the percentage of recovery should be as high as
possible, thus the one-sided transformation for maxi-
mum purpose is suggested as follows:
d
1i
=
0,
ˆ
π
i
(%MC) < L
ˆ
π
i
(%MC)−L
U−L
, L ≤
ˆ
π
i
(%MC) ≤ U
1,
ˆ
π
i
(%MC) > U
where L = 0.3393 and U = 0.7914. The above de-
sirability function suggests that it is highly undesired
when
ˆ
π
i
(%MC) is smaller than the lower bound, and
it is highly recommended when
ˆ
π
i
(%MC) is larger
than the upper bound.
Table 1: High-performance Liquid Chromatography
(HPLC) Experiment.
Design Cont. R Binary R
B E F %MC t
R
%MC
′
t
′
R
Prodigy 26 45 101.6 11.500 +1 +1
Prodigy 24 41 101.7 13.000 +1 +1
Alltech 24 45 101.6 9.833 +1 −1
Alltech 26 45 101.9 9.483 +1 −1
Alltech 24 41 101.8 10.317 +1 +1
Prodigy 24 45 101.1 12.567 +1 +1
Prodigy 24 45 101.1 12.083 +1 +1
Alltech 26 45 101.6 8.417 +1 −1
Alltech 26 41 98.4 9.200 −1 −1
Prodigy 26 41 99.7 13.800 −1 +1
Prodigy 26 41 99.7 13.317 −1 +1
Alltech 24 41 102.3 11.150 +1 +1
Norminal Value of %MC = 100%
Norminal Value of t
R
= 9.9 min
To obtain upper and lower bounds of
ˆ
t
R
, a similar
logistic regresion model is used. Among 12 predicted
responses, the maximum and minimum of them are
0.8410 and 0.2688 respectively. It is obvious that
the analysis time should be as short as possible, thus
the one-sided transformation for minimum purpose is
suggested as follows:
d
i
=
1,
ˆ
π
i
(t
R
) < L
U−
ˆ
π
i
(t
R
)
U−L
, L ≤
ˆ
π
i
(t
R
) ≤ U
0,
ˆ
π
i
(x) > U
where L = 0.2688 and U = 0.8410. The above de-
sirability function suggests that it is highly undesired
when
ˆ
π
i
(t
R
) is larger than the upper bound, and it is
highly recommended when
ˆ
π
i
(t
R
) is smaller than the
lower bound.
5 SOME DISCUSSIONS AND
CONCLUDING REMARKS
This paper proposes a modified method for desirabil-
ity function approach to deal with the data with mul-
tiple Bernoulli-distributed responses. The proposed
method avoids the breakdown on the formulation of
the individual desirability function due to the diffi-
culties on providing a meaningful explanation to the
arithmetic operations.
The main modification is on the model building
procedure. For each response, instead of using ordi-
nary linear regression, the logistic regression model is
suggested. Then the probability of having the original
response to be +1 is transformed back from the logit
of the model. This probability is then used for be-
ing transformed into the individual desirability func-
tion. Since there are only two possible choices on the
original response, only one-sided transformation, ei-
ther maximum or minimum, is needed to consider. An
example is used for demonstrating how the proposed
method works.
The popularity of the desirability function in in-
dustrial applications has not gone unnoticed and use
of the desirability function is beginning to appear in
other areas like clincial trials and social science. The
researchese in both area contain plenty of data with
multiple binary responses and the compromise setting
of explanatory variables are desired. Thus the pro-
posed method in this paper will hopefully provide a
solution to these researches.
The method proposed in this paper sounds similar
to some modeling approaches like multi-response lo-
gistic regression and/or penalized logistic regression.
However, the main difference between them is that
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
130

the regression method aims at modeling multiple re-
sponses simultaneously, but it is possible to suggest
the estimates of a factor with different signs, which
causes confusions when one attempts to set up the fac-
tor levels of the experiment. Desirability function is
a compromise method that aggregates responses into
one single quantity, and all factors are set optimally on
this aggregated quantity. Thus, only one set of com-
promise factor setting will be returned and it reduces
the confusion when one attempts to set up the experi-
ment.
Bernoulli-distributed responses, which consists of
only two possible outcomes, is the simplest case for
categorical type variables. One promising direction to
the next step is to develop a framework of desirabil-
ity function approach for categorical responses. It is
interesting to investigate in how to couple the varia-
tion information with the categorical responses when
repeated experiments are done. Since these responses
are not continuous, transformations on the responses
and their variations are required for proper analysis.
Furthermore, the example in this paper has been an-
alyzed and thus comparable. It is desired to perform
more simulations on some new real-life applications
in order to check the efficiency of the generalized
method for categorical responses.
ACKNOWLEDGEMENTS
This work was supported by National Science Coun-
cil of Taiwan ROC grant numbers 100-2118-M-001-
002-MY2 and 101-2811-M-001-001. The authors
would like to thank two referees for their valuable
suggestions and comments to this paper.
REFERENCES
Candes, E. and Tao, T. (2006). The dantzig selector: Statis-
tical estimation when p is much larger than n. Annals
of Statistics, 35:2313–2351.
Derringer, G. (1994). A balancing act: Optimizing a prod-
uct’s properties. Quality Progress, 6:51–58.
Derringer, G. and Suich, R. (1980). Simultaneous optimiza-
tion of several response variables. Journal of Quality
Technology, 12:214–219.
Harrington, E. (1965). The desirability function. Industrial
Quality Control, 4:494–498.
Khuri, A. (1996). Multiresponse surface methodology.
Handbook of Statistics: Design and Anlysis of Exper-
iments (Ghosh, A., Rao C.R. (Eds.)), 13:377–406.
Khuri, A. and Conlon, M. (1981). Simultaneous optimiza-
tion of multiple responses represented by polynomial
regression functions. Technometrics, 23:363–375.
Kim, K. and Lin, D. (2000). Simultaneous optimization
of multiple responses by maximining exponential de-
sirability functions. Journal of the Royal Statistical
Society C, 49:311–325.
Kim, K. and Lin, D. (2006). Optimization of multiple re-
sponses considering both location and dispersion ef-
fects. European Journal of Operational Research,
169:133–145.
Phoa, F. (2012a). The stepwise response refinement
screener (srrs). (in review).
Phoa, F. (2012b). The stepwise response refinement
screener (srrs) and its applications to analysis of
factorial experiments. Proceedings of International
Conference on Pattern Recognition Applications and
Methods (ICPRAM), 1:157–161.
Phoa, F., Pan, Y., and Xu, H. (2009). Analysis of supersat-
urated designs via dantzig selector. Journal of Statis-
tical Planning and Inference, 139:2362–2372.
Pignatiello, J. (1993). Strategies for robust multiresponse
quality engineering. IIE Transactions, 25:5–15.
Tibshirani, R. (1996). Regression shrinkage and selection
via the lasso. Journal of the Royal Statistical Society
B, 58:267–288.
Vande Heyden, Y., Jimidar, M., Hund, E., Niemeijer, N.,
Peeters, R., Smeyers-Verbeke, J., Massart, D., and
Hoogmartens, J. (1999). Determination of system
suitability limits with a robustness test. Journal of
Chromatography A, 845:145–154.
Vining, G. G. (1998). Compromise approach to multire-
sponse optimization. Journal of Quality Technology,
30:309–313.
Xu, K., Lin, D., Tang, L., and Xie, M. (2004). Multi-
response system optimization using a goal attainment
approach. IIE Transactions, 36:433–445.
DesirabilityFunctionApproachontheOptimizationofMultipleBernoulli-distributedResponse
131
