
Experimental Evaluation of the Effects of Manipulation by Merging in
Weighted Voting Games
Ramoni O. Lasisi and Vicki H. Allan
Department of Computer Science, Utah State University, Logan, U.S.A.
Keywords:
Agents, Weighted Voting Games, Power Indices, Manipulation, Merging.
Abstract:
Weighted voting games are subject to a method of manipulation, called merging. This manipulation involves
a coordinated action among some agents who come together to form a bloc by merging their weights in
order to have more power over the outcomes of games. We conduct careful experimental investigations to
evaluate the opportunities for beneficial merging available for strategic agents using two prominent power
indices: Shapley-Shubik and Banzhaf indices. Previous work has shown that finding a beneficial merge is NP-
hard for both the Shapley-Shubik and Banzhaf power indices, and leaves the impression that this is indeed
so in practice. However, results from our experiments suggest that finding a beneficial merge is relatively
easy in practice. Furthermore, while it appears impossible to stop manipulation by merging for a given game,
controlling the quota ratio is desirable. Thus, we deduce that a high quota ratio reduces the percentage of
beneficial merges. Finally, we conclude that the Banzhaf index may be more desirable to avoid manipulation
by merging, especially for high quota ratios.
1 INTRODUCTION
Weighted Voting Games (WVGs) are classic coop-
erative games which provide compact representation
for coalition formation models in human societies
and multiagent systems. Each agent in a WVG has
an associated weight. A subset of agents whose to-
tal weight is at least the value of a specified quota
is called a winning coalition. The weights of agents
in a game correspond to resources or skills avail-
able to agents, while the quota is the amount of re-
sources or skills required for a task to be accom-
plished. For example, in academia, professors put
their resources (i.e., weights) together to publish ar-
ticles (i.e., quota). The relative power of each agent
in WVGs reflects its significance in the elicitation
of a winning coalition. To evaluate players’ power
in such games, prominent power indices such as
the Shapley-Shubik (Shapley and Shubik, 1954) and
Banzhaf (Banzhaf, 1965) indices are commonly used.
Recently, there is much interest in manipula-
tion (i.e., dishonest behaviors) by strategic players
in WVGs. These manipulations involve an agent or
agents misrepresenting their identities in anticipation
of gaining more power at the expense of other agents
in a game. See (Bachrach and Elkind, 2008; Aziz
and Paterson, 2009; Lasisi and Allan, 2010; Aziz
et al., 2011; Lasisi and Allan, 2011). In manipula-
tion by merging, which is also known as alliance or
collusion, two or more agents voluntarily merge their
voting weights to form a single bloc (Felsenthal and
Machover, 1998; Felsenthal and Machover, 2002). In
a beneficial merge, merged agents are compensated
commensurate with their share of the power gained
by the bloc. The agents whose weights are merged
into a bloc are referred to as assimilated agents.
(Yokoo et al., 2005) consider collusion in open
anonymous environments, such as the internet. They
show that collusion in such environments can be dif-
ficult to detect. Thus, the increased use of online sys-
tems such as trading systems and peer-to-peer net-
works, where WVGs are also applicable, means that
manipulation by merging remains an important chal-
lenge.
To provide insights into understanding the prob-
lem of manipulation by merging in WVGs, first, we
recall that the problem of computing the Shapley-
Shubik and Banzhaf indices is NP-hard (Matsui and
Matsui, 2001). (Aziz et al., 2011) have also shown
that determining if there exists a beneficial merge
for the manipulators is NP-hard using either of the
two indices to compute agents’ power. Although this
worst case complexity for manipulation by merging
is daunting, it is possible that real instances of WVGs
196
O. Lasisi R. and H. Allan V..
Experimental Evaluation of the Effects of Manipulation by Merging in Weighted Voting Games.
DOI: 10.5220/0004229401960203
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 196-203
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

are easy to manipulate. We note that real WVGs are
small enough that exponential amount of work may
not deter manipulators from participating in manipu-
lation by merging. Thus, according to (Keijzer et al.,
2010), the number of players in most real life exam-
ples of WVGs is between 10 and 50. Hence, manipu-
lations may, in some cases, be achieved in practice.
A careful investigation of effective heuristics for
manipulating such games by merging are yet to be
researched (Aziz and Paterson, 2009). This, we ar-
gue, may be primarily due to the inherent difficulty
of the problem. This is because the ability to find
beneficial merges depends on the characteristics of
the game. Some games have little opportunity for
merging while others could have many beneficial
merges. So, in contrast to the work of (Aziz et al.,
2011), in this paper, we study experimental evalua-
tion of the effects of manipulation by merging using
various parameters of the games to analyze opportuni-
ties for beneficial merging for the manipulators. This
will provide insight into understanding the problem to
both provide insights for heuristics and guide the deci-
sions of game designers. Our evaluation is carried out
using two prominent power indices: Shapley-Shubik
and Banzhaf indices, to compute agents’ power.
The NP-hardness results of finding a beneficial
merge of the previous work for both the Shapley-
Shubik and Bazhaf indices leave the impression that
this is indeed so in practice. While finding the best
merging may be difficult, results from our experi-
ments suggest that finding a beneficial merge is rel-
atively easy in practice. While we may be powerless
to stop manipulation by merging for a given game,
we suggest controlling quota ratio, which is the per-
centage of weight needed to form a winning coali-
tion. The game designer may be able to control the
quota ratio. Thus, we deduce that when the quota ratio
of a game is high, the percentage of beneficial merges
goes down. Finally, we conclude that the Banzhaf
power index may be more desirable than the Shapley-
Shubik power index to avoid manipulation by merg-
ing, especially for high values of the quota ratios.
2 RELATED WORK
(Felsenthal and Machover, 2002) characterize situ-
ations when it is advantageous or disadvantageous
for agents to merge into a bloc, and show that us-
ing the Shapley-Shubik index, merging can be ad-
vantageous or disadvantageous. (Aziz and Paterson,
2009) focus on the complexity of finding advanta-
geous merging. They show that for unanimity WVGs,
it is disadvantageous for a coalition to merge using
the Shapley-Shubik index to compute payoff. Also,
determining if there exists a beneficial merge is NP-
hard for the Shapley-Shubik index. (Lasisi and Al-
lan, 2011) considers empirical evaluation of the extent
of susceptibility of three indices, namely, Shapley-
Shubik, Banzhaf, and Deegan-Packel indices to ma-
nipulation when agents engage in merging. Their re-
sults show that the Shapley-Shubik index is the most
susceptible to manipulation via merging among the
three indices. Furthermore, a recent work of (Lasisi
and Allan, 2012) proposes a search-based approach
to manipulation by merging. They show that manipu-
lators need to do only a polynomial amount of work
to find improved benefits when the size of the ma-
nipulators’ bloc is restricted to a constant 2 ≤ k < n,
where n is the number of agents in the WVG. The au-
thors then present a pseudopolynomial-time enumer-
ation algorithm that manipulators may use to find a
much improved power gain over a random approach
using both the Shapley-Shubik and Banzhaf indices
to compute agents’ power.
It is important to note that none of these papers
deal with the experimental evaluation and analysis of
the type of beneficial merging that we study here.
3 PRELIMINARIES
3.1 Weighted Voting Games
Let I = { 1, ··· , n} be a set of n agents and the
corresponding positive weights of the agents be
{w
1
, ··· , w
n
}. Let a coalition S ⊆ I be a non-empty
subset of agents. A WVG G, with quota q involv-
ing agents I, is represented as G = [w
1
, . . . , w
n
;q]. We
assume that w
1
≥ w
2
≥ . . . ≥ w
n
. Note that this as-
sumption does not affect the definition of the game
or the generality of our results. Denote by w(S), the
weight of a coalition, S, derived as the summation of
the weights of agents in S, i.e., w(S) =
∑
j∈S
w
j
. A
coalition, S, wins in game G if w(S) ≥ q, otherwise
it loses. WVGs belong to the class of simple voting
games. In simple voting games, each coalition, S, has
an associated function v : S → {0, 1}. The value 1 im-
plies a win for S and 0 implies a loss. So, v(S) = 1 if
w(S) ≥ q, and 0 otherwise.
3.2 Power Vectors
(de Nijs and Wilmer, 2012) propose the use of power
vectors to evaluate heuristics for the well-known in-
verse problem (Fatima et al., 2008; Keijzer et al.,
2010) using the Banzhaf power index. We use power
vectors in this paper to illustrate the effects of small
ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames
197

changes in the weights of agents on their correspond-
ing powers in WVGs.
Define a power vector for a WVG G of n agents
as follows. Consider the weights of agents in G in a
non-increasing order. The power vector of G is an n-
dimensional vector v ∈ R
n
of the power of each of the
agents listed in order.
3.3 Shapley-Shubik Power Index
The Shapley-Shubik index quantifies the marginal
contribution of an agent to the grand coalition (i.e.,
a coalition of all the agents). Each permutation of the
agents is considered. We term an agent pivotal in a
permutation if the agents preceding it do not form a
winning coalition, but by including this agent, a win-
ning coalition is formed. Shapley-Shubik index as-
signs power to each agent based on the proportion
of times it is pivotal in all permutations. We specify
the computation of the index using notation of (Aziz
et al., 2011). Denote by π, a permutation of the agents,
so π : {1, . . . , n} → { 1, . . . , n}, and by Π the set of all
possible permutations. Denote by S
π
(i) the predeces-
sors of agent i in π, i.e., S
π
(i) = { j : π( j) < π(i)}. The
Shapley-Shubik index, ϕ
i
(G), for each agent i in a
WVG G is
ϕ
i
(G) =
1
n!
∑
π∈Π
[v(S
π
(i) ∪ {i}) − v(S
π
(i))]. (1)
3.4 Banzhaf Power Index
An agent i ∈ S ⊆ I is referred to as being critical in
a winning coalition, S, if w(S) ≥ q and w(S\{ i}) <
q. The Banzhaf power index computation for an agent
i is the proportion of times i is critical compared to
the total number of times any agent in the game is
critical. The Banzhaf index, β
i
(G), for each agent i in
a WVG G is given by
β
i
(G) =
η
i
(G)
∑
j∈I
η
j
(G)
(2)
where η
i
(G) is the number of coalitions for which
agent i is critical in G.
4 PROBLEM DEFINITION
4.1 Problem Formalization
Let k and n be integers such that 2 ≤ k ≤ n. Let
I = {1, ··· , n} be a set of n agents and the correspond-
ing weights of the agents be {w
1
, ··· , w
n
}, where
w
i
∈ Z. Let G = [w
1
, . . . , w
n
;q] be a WVG of n agents
with quota q ∈ Z. Consider a manipulators’ coalition
C of k agents which is a k-subset of the n-set I. We as-
sume that C contains distinct k elements chosen from
I. Suppose the manipulators in C merge into a single
bloc denoted by &C, i.e., agents i ∈ C have been as-
similated into the bloc &C, then, we have a new set
of agents in the game after merging. Thus, the initial
game G of n agents has been altered by the manipu-
lators to give a new WVG G
′
of n− k + 1 agents con-
sisting of the bloc and other agents not in the bloc i.e.,
I\C. Note that the weights of the non manipulators
and the quotas in the two games remain the same.
Let φ be any of Shapley-Shubik or Banzhaf power
index. Denote by (φ
1
(G), . . . , φ
n
(G)) ∈ [0, 1]
n
the
power of agents in WVG G. Thus, for the manipu-
lating agents i ∈ C with power φ
i
(G) in game G, the
sum of the power of the k manipulators is
∑
i∈C
φ
i
(G),
while that of the bloc formed by the manipulators in
game G
′
is φ
&C
(G
′
). The ratio τ =
φ
&C
(G
′
)
∑
i∈C
φ
i
(G)
gives a
factor of the power gained or lost by the manipulators
when they alter game G to give G
′
. The power index,
φ, is said to be susceptible to manipulation in WVG
G if there exists a G
′
such that τ > 1; the merging is
termed advantageous or beneficial. If τ < 1, then the
merging is disadvantageous or non-beneficial, while
the merging is neutral when τ = 1.
4.2 Examples of Merging in WVGs
We have used the Shapley-Shubik power index for
illustration in these examples. The manipulators and
their powers are shown in bold.
Example 1. Beneficial Merging
Let G = [8, 8, 8, 6, 5, 5, 4,2,2, 2;28] be a WVG
of ten agents. The power vector of this game is
[0.167, 0.167, 0.167, 0.119, 0.099, 0.099, 0.067, 0.039,
0.039, 0.039]. Thus, the manipulators’ coalition
C = {3, 6, 7, 8, 9, 10}. The cumulative power of these
manipulators is 0.4481. Suppose the manipulators
merge their weights to form a bloc &C and alter G to
give G
′
= [23, 8, 8, 6, 5;28]. The power of the bloc is
ϕ
&C
(G
′
) = ϕ
1
(G
′
) = 0.8000 > 0.4481. The factor of
power gained by the manipulators is τ =
0.8000
0.4481
= 1.8.
Note that we have implicitly assumed that agents
in the blocs formed are working cooperatively and
have transferable utility. Thus, proceeds from merg-
ing can easily be distributed among the manipula-
tors. For instance, in this example, each manipula-
tors may first be assign a payoff equal to what it
would get in the original game G, then, the gain (i.e.,
0.8000 − 0.4481 = 0.3519) derived from the altered
game G
′
can then be distributed among the members
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
198

of C using different solution concepts for revenue dis-
tribution from coalitional game theory.
Not all manipulation by merging are benefi-
cial. Example 2 illustrates an example of a non-
beneficial merge for the manipulators.
Example 2. Non-beneficial Merging
Let G = [10, 9, 9, 9, 8, 7, 6, 6, 2,1;56] be a WVG
of ten agents. The power vector of this game
is [0.135, 0.121, 0.121, 0.121, 0.118, 0.118, 0.118,
0.118, 0.022, 0.008]. Thus, the manipulators’
coalition C = {4, 6, 8, 9, 10}. The cumulative
power of these manipulators is 0.3869. Sup-
pose these manipulators merge their weights
to form a single bloc &C and alter G to give
G
′
= [25, 10, 9, 9, 8, 6;56]. The power of the bloc is
ϕ
&C
(G
′
) = ϕ
1
(G
′
) = 0.3333 < 0.3869. The factor of
power lost by the manipulators is τ =
0.3333
0.3869
= 0.86.
5 MERGING PREDICTION
5.1 Using Power Vectors
Using power vectors, we provide further examples
to illustrate manipulation by merging. We have used
power vectors to illustrate the effects of small changes
in the weights of agents on their corresponding pow-
ers in WVGs. The Shapley-Shubik index is used in
this example. The small changes in the weight of
agents are related to weights changes when two or
more agents merge their weights to form a bloc,
thus providing some insights into merging. A cru-
cial observation is that we can have many games hav-
ing the same power vector. For example, the follow-
ing WVGs: [11, 9, 4;12], [11, 8, 5;12], [11, 7, 6;12],
[10, 9, 5;12], [10, 8, 6;12], and [10, 7, 7;12] all have
the same power vector [0.33, 0.33, 0.33], even though
the weights’ distribution of agents in the games differ.
In Figure 1, we consider all WVGs of 3 agents
such that the total weights of the agents in each
game is 24. Figures 1(a), 1(b), and 1(c) are for the
cases when the quotas q of the games are 12, 16,
and 18, respectively. The y-axis indicates the possi-
ble weights of the first agent while the x-axis indi-
cates the possible weights of the second agents in the
games. Note that since agents weights are given in
non-increasing order, the possible weights for the sec-
ond agent are dependent on the weights of the first
agent. The possible weights of the third agents are
not shown since they can implicitly be derived hav-
ing known the weights of the first two agents.
Similar to only the 4 power vectors that are attain-
able in WVGs of 3 players using the Banzhaf index
(de Nijs and Wilmer, 2012), there are also 4 different
power vectors for these games when the number of
agents is 3 and using the Shapley-Shubikindex. These
power vectors are coded as 1, 2, 3, and 4 below:
1 : [0.33, 0.33, 0.33]
2 : [0.50, 0.50, 0.00]
3 : [0.67, 0.17, 0.17]
4 : [1.00, 0.00, 0.00]
with the games of each power vector representing ap-
propriate regions shaded in Figure 1. It is easy to
observe the following facts which have impacts on
weight changes as it relates to merging:
• The number of different power vectors is a func-
tion of the number of agents, n, in the games.
• The size of the region (associated with a particular
power vector) changes with the quota.
• Some weight vectors are volatile to changes
with respect to small changes in weight (such
as [11, 7, 6;18]) while others are not (such as
[12, 11, 1;18]).
5.2 Difficulty of Merge Prediction
A visual description clarifies manipulation by merg-
ing in WVGs. We use the Shapley-Shubik power in-
dex for illustration. Consider a WVG of three agents
denoted by the following patterns: Agent 1 ( ),
Agent 2 ( ), and Agent 3 ( ). The weight of each
agent in the game is indicated by the associated length
of the pattern. A box in the pattern corresponds to a
unit weight. Each row represents a permutation. Sup-
pose all permutations of the three agents are given as
shown in Figure 2. We can use the same figure to con-
sider a range of quotas from 1 to 6 for the game. The
Shapley-Shubik indices of the three agents are com-
puted from the figure and shown in the associated ta-
ble of the figure. These power indices for the agents
in the game correspond to using various values of the
quota for the same weights of the agents.
Consider a manipulation where Agent 1 and
Agent 3 merge their weights to form a new agent,
say, Agent X. In this case, Agent 1 and Agent 3
cease to exist since they have been assimilated by
Agent X. Thus, we have only two agents (Agent X
and Agent 2) in the altered WVG. Figure 3 shows the
results of the merging between Agent 1 and Agent
3. Notice that the number of rows has been reduced
to two, as there are now only two possible order-
ings. Consider the cases when the quota of the game is
1 or 6, the power of the assimilated agents for Agent
X from Figure 2 shows that Agent 1 and Agent 3 each
has a power of
1
3
for a total power of
2
3
. The power of
ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames
199

Figure 1: Using power vectors to illustrate the effects of small changes in the weights of agents on their corresponding
Shapley-Shubik powers in WVGs.
Figure 2: Six permutations of 3 agents and the power in-
dices of the agents for values of quota from q = 1 to q = 6.
Agent X which assimilates these two agents in the two
cases is each
1
2
<
2
3
. Also, the power of the manipu-
lators stays the same for the cases where the quota is
either 2 or 5. Specifically, the sum of the powers of
Figure 3: Manipulation by merging between Agent 1 and
Agent 3 (from Figure 2) to form a new Agent X. The indices
of Agent X and Agent 2 computed by Shapley-Shubik index
after merging for various values of quota are also shown.
Agent 1 and Agent 3 is
1
2
for these cases. This is also
true of Agent X for these cases. Finally, for the cases
where the quota of the game is 3 or 4, the power of
Agent X is 1 which is greater than
5
6
, the sum of the
powers of Agent 1 and Agent 3 in the original game.
Note the difficulty of predicting what will happen
when manipulators engage in merging. This illustra-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
200
tion also shows that the choice of the quota of a game
is crucial in determining the distribution of power of
agents in a WVG. An apparent question that concerns
the manipulators from the illustration above is the fol-
lowing : Can effective merging heuristics be found
even though predicting beneficial merging is difficult?
6 EXPERIMENTS
6.1 Simulation Environments
We perform experiments to provide understanding
and analysis of the opportunities for beneficial merg-
ing by manipulators in WVGs. We randomly gener-
ate WVGs. The weights of agents in each game are
chosen such that all weights are integers and drawn
from a Normal distribution, N(µ, σ
2
), where µ and σ
2
are the mean and variance. We have used µ = 50 and
several values of standard deviation σ from the set
{5, 10, . . . , 40}. The number of agents, n, in each of
the original WVGs is 10. For clarity of presentation,
we have restricted the number of assimilated agents,
k, in each game to 2. This is consistent with the as-
sumptions of previous work on merging (Aziz et al.,
2011; Lasisi and Allan, 2012) and coalition formation
(Shehory and Kraus, 1998), as manipulators’ blocs of
small sizes are easier to form, and more importantly
to the manipulators, they are less likely to be detected
by other agents in the games. Apart from this, we also
believethat an indepth understanding of this case (i.e.,
k = 2), will provide necessary background in under-
standing of the general case of when k > 2.
We have used a total of 200 distinct WVGs for
our experiments. For each game, we vary the quota
of the game from
1
2
w(I) + 1 to w(I) in steps of 10,
where w(I) is the sum of the weights of all agents in
the game. We then compute the factor of increment
for each assimilated bloc of size 2 in a game using
the two power indices. The evaluation is carried out
for the proportion of beneficial merges in a game and
the quota ratio,
q
w(I)
=
quota
total weight
. The quota ratios for
the experiments range from 0.5 to 1.0, and indicate
the fraction of the total weight needed for the quo-
tas. A quota ratio of 1.0 suggests the existence of a
type of WVGs referred to as unanimity WVGs, where
all agents in a game are needed to form a winning
coalition. Thus, a winning coalition always exists in
the games. In other words, the quota ratio is a measure
of the percentage of weight needed to form a winning
coalition.
We consider all possible manipulators’ blocs of
size 2. The percentage of beneficial merge for a quota
ratio is the fraction of cases whose factors of incre-
ment is greater than a specified value of τ. We tweak
τ using different values to see how the percentage
of beneficial merges varies and provide discussions
of the effects noticed in the next subsection. The
pseudocode to compute the percentage of beneficial
merges for each quota ratio is given in Figure 4.
percentBeneficialMerge(Agents I, WVG G,
τ
) {
for quota q of G from
1
2
w(I)+1 to w(I) step 10
successCount = 0;
totalCount = 0;
for each manipulators’ bloc b of size 2
compute factor of increment f for b
if f
> τ
then
successCount++;
totalCount++;
end for
quotaRatio = q / w(I);
percentBenefit = successCount / totalCount;
end for
}
Figure 4: Pseudocode to compute the percentage of benefi-
cial merges for each quota ratio.
6.2 Discussion of Simulation Results
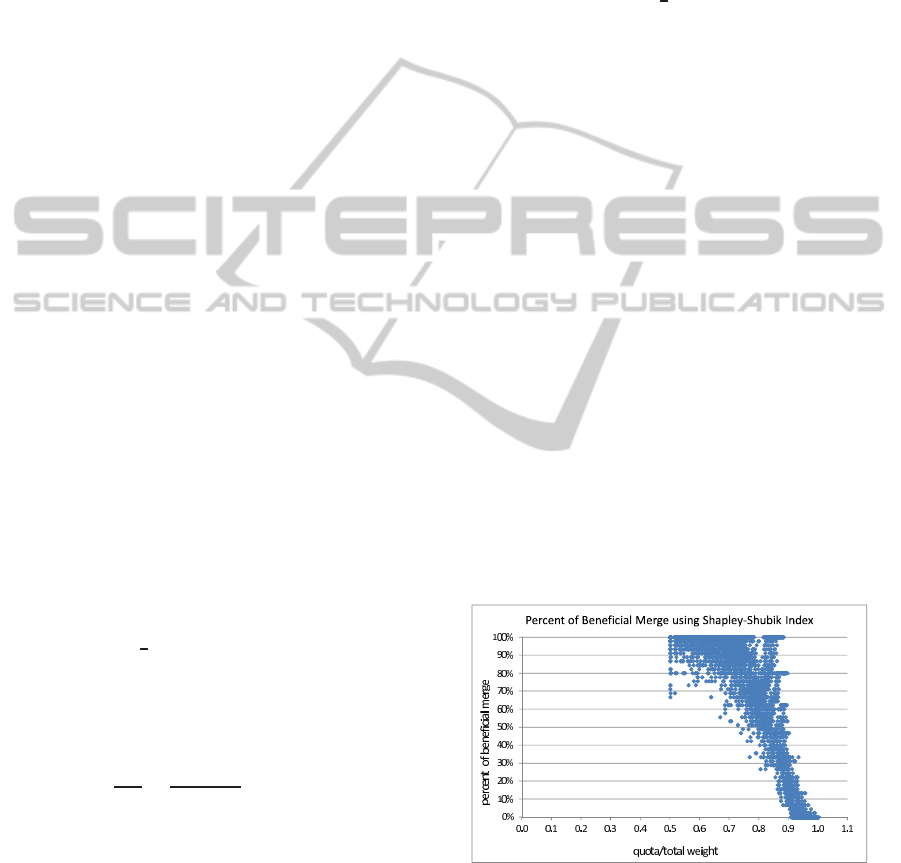
We present the results of our experiments. Figures 5
and 6 are indications of the opportunities for bene-
ficial merging available for the manipulators. The x-
axis is the quota ratio and the y-axis is the percentage
of beneficial merging available to the manipulators
when a beneficial merge is defined strictly as τ = 1,
i.e., a factor of power gain greater than 1.
Figure 5: Percentage of beneficial merging for various val-
ues of quota ratio when a beneficial merge is defined to have
a factor of power gain greater than 1.0 (Shapley-Shubik).
The theoretical results of (Aziz et al., 2011) on
merging show that finding a beneficial merge is NP-
hard for both the Shapley-Shubik and Bazhaf indices,
and leave us with the impression that this is indeed so
ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames
201
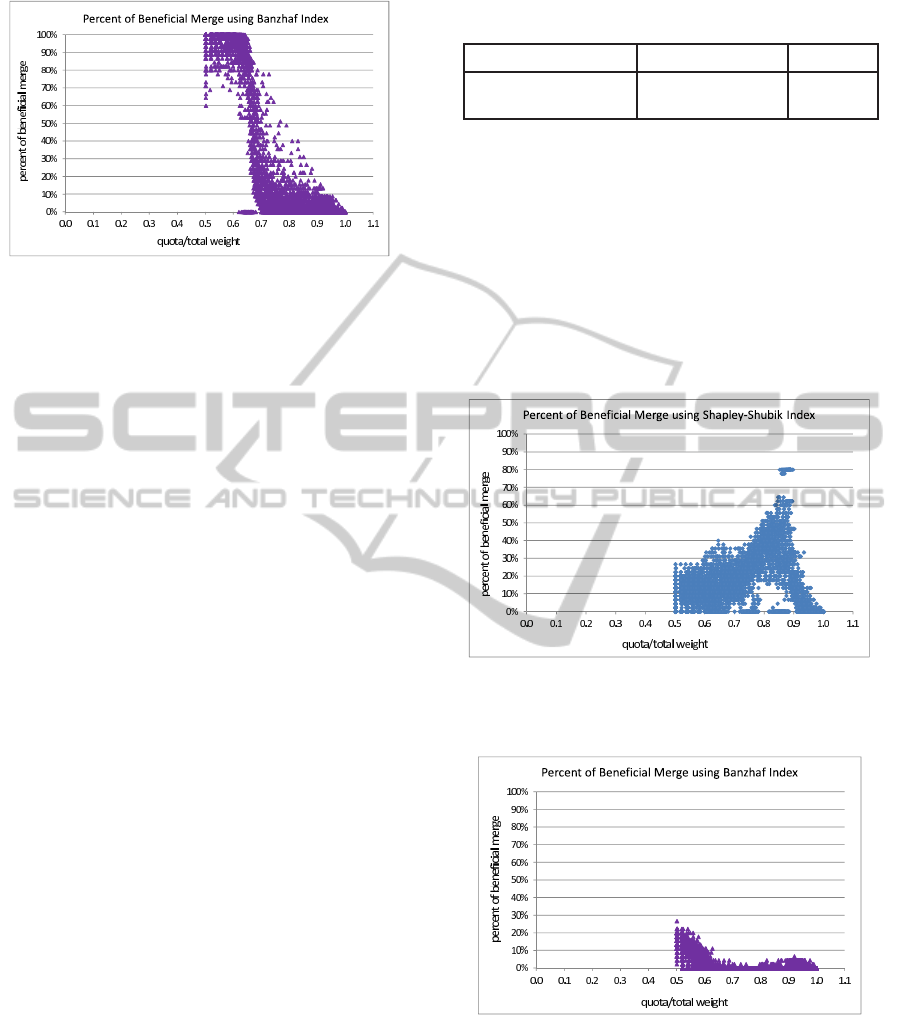
Figure 6: Percentage of beneficial merging for various val-
ues of quota ratio when a beneficial merge is defined to have
a factor of power gain greater than 1.0 (Banzhaf index).
in practice. Figures 5 and 6 show that finding a benefi-
cial merge is relatively easy in practice, at least for the
WVGs we considered, and restricting each manipula-
tors’ blocs to size 2. In reality, finding the best merg-
ing may not even be desirable, as it assumes every
agent will be willing to merge. Manipulators cannot
petition every agent to see if they are willing to merge,
as the manipulators would have announced their in-
tent to cheat. However, a dishonest agent may first
discover opportunities for beneficial merging before
suggesting such merge to other would-be manipula-
tors.
While it appears from the figures that we may
be powerless to stop merging for a given game, the
game designer may be able to control the quota. Thus,
a high quota ratio reduces the opportunities for dis-
honesty as the percentage of beneficial merges goes
down. Using the two indices to compute agents’
power, we can deduce from Figures 5 and 6 that the
Banzhaf index is more desirable to avoid cheating es-
pecially for high ratios. This is because the percent-
ages of beneficial mergings for high values of the
quota ratio using the Banzhaf index are smaller com-
pare to those of the Shapley-Shubik index. Table 1
shows the means and standard deviations of the fac-
tor of power gained by manipulators from Figures 5
and 6. This shows that, on average, manipulation by
merging is easier using the Shapley-Shubikindex than
using the Banzhaf index. This also indicates that the
Banzhaf index may be more desirable to avoid manip-
ulation in this situation.
For the second set of experiments, we consider
a more realistic scenario for the manipulators. Even
though we have defined a beneficial merge as a merge
in which manipulators have a power gain with τ >
1, manipulators may only be interested in beneficial
merge with appreciable gains as the risks of being de-
tected by the mechanism may exceed the anticipated
benefits. We have restricted the minimal beneficial
Table 1: The means and standard deviations of the factor of
power gained for Figures 5 and 6 using the two indices.
Indices Shapley-Shubik Banzhaf
Mean 1.142 1.062
Standard deviation 0.182 0.057
rate to τ = 1.05 or 1.10, and do not notice appreciable
change in the percentage of beneficial merging com-
pared with those of Figures 5 and 6. Thus, we do not
report them here.
However, for value of τ = 1.15, which represents
at least a 15% anticipated increment from the original
power of the manipulators, we noticed a sharp con-
trast from earlier results. This is an interesting and a
positive result for the designer of a game as it shows
that the percentageof beneficial merges drops for both
power indices. See Figures 7 and 8.
Figure 7: Percentage of beneficial merging for various val-
ues of quota ratio when a beneficial merge is defined to have
a factor of power gain greater than 1.15 (Shapley-Shubik).
Figure 8: Percentage of beneficial merging for various val-
ues of quota ratio when a beneficial merge is defined to have
a factor of power gain greater than 1.15 (Banzhaf index).
Consider Figure 7. The opportunities for benefi-
cial merge for the manipulators using the Shapley-
Shubik index may still be high, even when the factor
of power gained has been increased to τ = 1.15. How-
ever, for the case of the Banzhaf index (see Figure 8),
the maximum percentage of beneficial merge avail-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
202

able for the manipulators is considerably less. We ar-
gue that it is not unlikely that low percentage of bene-
ficial merge may discourage manipulators in engaging
in manipulation by merging if these conditions that
we describe prevail and also using the Banzhaf power
index to compute agents’ power.
7 CONCLUSIONS
This paper considers experimental evaluation of the
effects of manipulation by merging in weighted vot-
ing games. We conduct careful experimental investi-
gations and analyses of the opportunities for benefi-
cial merging available for strategic agents to engage
in such manipulation using two well-known power
indices, the Shapley-Shubik and Banzhaf power in-
dices to compute agents’ power. The following gives
account of our main contributions.
First, we examine effects of small changes in the
weights of agents on their corresponding powers in
weighted voting games. This is illustrated by show-
ing that power vectors are often unchanged. Second,
we argue and provide empirical evidence to show
that despite finding the optimal beneficial merge is
an NP-hard problem for both the Shapley-Shubik and
Banzhaf power indices, finding beneficial merge is
relatively easy in practice. Hence, there may be little
deterrent to manipulation by merging in practice us-
ing the NP-hardness results. Third, while it appears
that we may be powerless to stop manipulation by
merging for a given game, we suggest a measure,
termed quota ratio, that the game designer may be
able to control. Thus, we deduce that a high quota
ratio decreases the number of beneficial merges. Fi-
nally, using the two power indices to compute agents’
power, we conclude that the Banzhaf index may be
more desirable to avoid manipulation by merging, es-
pecially for high values of quota ratios.
There are several areas of ongoing research on
this problem. First, we seek to expand our experimen-
tal evaluations to consider and understand the gen-
eral case of manipulators’ blocs of size greater than
2. Second, we seek to understand the effects of other
parameters of our experiments on the opportunities
for beneficial merging for the manipulators. Finally,
we also seek to provide careful investigations of ef-
fective heuristics for manipulation by merging.
ACKNOWLEDGEMENTS
This work is supported by NSF research grant
#0812039 entitled “Coalition Formation with Agent
Leadership”.
REFERENCES
Aziz, H., Bachrach, Y., Elkind, E., and Paterson, M. (2011).
False-name manipulations in weighted voting games.
Journal of Artificial Intelligence Research, 40:57–93.
Aziz, H. and Paterson, M. (2009). False-name manipula-
tions in weighted votinggames: splitting, merging and
annexation. In 8th Intl. Conf. of AAMAS, pages 409–
416, Budapest, Hungary.
Bachrach, Y. and Elkind, E. (2008). Divide and con-
quer: false-name manipulations in weighted voting
games. In 7th Intl. Conf. of AAMAS, pages 975–982,
Estoril, Portugal.
Banzhaf, J. (1965). Weighted voting doesn’t work: a math-
ematical analysis. Rutgers Law Review, 19:317–343.
de Nijs, F. and Wilmer, D. (2012). Evaluation and improve-
ment of Laruelle-Widgr´en inverse Banzhaf approxi-
mation. CoRR, abs/1206.1145.
Fatima, S., Wooldridge, M., and Jennings, N. R. (2008). An
anytime approximation method for the inverse Shap-
ley value problem. In 7th Intl. Conf. of AAMAS, pages
935–942, Portugal.
Felsenthal, D. S. and Machover, M. (1998). The Measure-
ment of Voting Power: Theory and Practice, Problems
and Paradoxes. Edward Elgar, Cheltenham.
Felsenthal, D. S. and Machover, M. (2002). Annexation
and alliances: when are blocs advantageous a priori.
Social Choice and Welfare, 19(2):295–312.
Keijzer, B., Klos, T., and Zhang, Y. (2010). Enumeration
and exact design of weighted voting games. In 9th Intl.
Conf. of AAMAS, pages 391–398, Toronto, Canada.
Lasisi, R. O. and Allan, V. H. (2010). False name manip-
ulations in weighted voting games: Susceptibility of
power indices. In 13th Workshop on Trust in Agent So-
cieties of AAMAS, pages 139–150, Toronto, Canada.
Lasisi, R. O. and Allan, V. H. (2011). Annexations and
merging in weighted voting games - the extent of sus-
ceptibility of power indices. In 3rd Intl. Conf. of
ICAART, pages 124–133, Rome, Italy.
Lasisi, R. O. and Allan, V. H. (2012). A search-based ap-
proach to annexation and merging in weighted voting
games. In 4th Intl. Conf. of ICAART, pages 44–53,
Vilamoura, Algarve, Portugal.
Matsui, Y. and Matsui, T. (2001). NP-completeness for cal-
culating power indices of weighted majority games.
Theoretical Computer Science, 263((1-2)):305–310.
Shapley, L. S. and Shubik, M. (1954). A method for evalu-
ating the distribution of power in a committee system.
American Political Science Review, 48:787–792.
Shehory, O. and Kraus, S. (1998). Methods for task allo-
cation via agent coalition formation. Artificial Intelli-
gence, 101(1-2):165–200.
Yokoo, M., Conitzer, V., Sandholm, T., Ohta, N., and
Iwasaki, A. (2005). Coalitional games in open anony-
mous environments. In American Association for Ar-
tificial Intelligence, pages 509–514.
ExperimentalEvaluationoftheEffectsofManipulationbyMerginginWeightedVotingGames
203
