
Inverse of Lorentzian Mixture for Simultaneous Training of Prototypes
and Weights
Atsushi Sato and Masato Ishii
Information and Media Processing Laboratories, NEC Corporation 1753,
Shimonumabe, Nakahara-ku, Kawasaki, Japan
Keywords:
Lorentzian Mixture, Nearest Neighbor, Loss Minimization, Bayes Decision Theory, Machine Learning.
Abstract:
This paper presents a novel distance-based classifier based on the multiplicative inverse of Lorentzian mix-
ture, which can be regarded as a natural extension of the conventional nearest neighbor rule. We show that
prototypes and weights can be trained simultaneously by General Loss Minimization, which is a generalized
version of supervised learning framework used in Generalized Learning Vector Quantization. Experimental
results for UCI machine learning repository reveal that the proposed method achieves almost the same as
or higher classification accuracy than Support Vector Machine with a much fewer prototypes than support
vectors.
1 INTRODUCTION
Distance-based classifiers have been widely used in
real applications, because they achieve good perfor-
mance in spite of their simple structures with a few
prototypes. One popular learning algorithm of pro-
totypes is Learning Vector Quantization (LVQ) (Ko-
honen, 1995), and the margin-based theoretical anal-
ysis has proved that LVQ is a family of large mar-
gin classifiers (Crammer et al., 2003). In the early
stage of LVQ research, learning algorithms were im-
proved by heuristic approaches. However, improve-
ments have been conducted based on loss minimiza-
tion, since Generalized Learning Vector Quantization
(GLVQ) (Sato and Yamada, 1996; Sato, 1998) was
proposed. One of the major improvements concerns
the choice of an appropriate distance measure (Ham-
mer and Villmann, 2002; Schneider et al., 2009; Vill-
mann and Haase, 2011).
Meanwhile, kernel classifiers have been investi-
gated, and Support Vector Machine (SVM) (Cortes
and Vapnik, 1995) has become one of the powerful
classification method. Many works have shown that
SVM outperforms conventional classifiers. Exten-
sions of GLVQ by means of kernel functions have
been also investigated (Qin and Suganthan, 2004;
Sato, 2010), and the experiments reveal that the ex-
tended models achieve almost the same classification
accuracy as SVM. However, only weights for the ker-
nels are trained, and positions of prototypes are never
changed in these models, like in SVM. This may lead
to the limit of classification capability, and to the in-
crease of the number of prototypes.
It seems to be natural to train prototypes and their
weights simultaneously to achieve good classifica-
tion performance with a fewer prototypes. A learn-
ing method of prototypes as well as weights has been
proposed (Karayiannis, 1996), but it cannot be suit-
able for classification problems, because it was for-
mulated through unsupervised learning. One possible
alternative is to repeat adding and removing proto-
types during learning to decrease errors (Grbovic and
Vucetic, 2009), but the optimality cannot be ensured,
because the weights for the prototypes are estimated
by a heuristic approach.
In order to train prototypes and their weights
through supervised learning framework, this paper
presents a novel distance-based classifier by utiliz-
ing the multiplicative inverse of Lorentzian mixture.
Lorentzian has been evaluated as a response function
instead of sigmoid in multi-layered neural networks
(Giraud et al., 1995), but in this paper, we utilize it
for nearest neighbor classifiers. We show that the pro-
posed classifier can be regarded as a natural extension
of the conventional nearest neighbor rule. We also
show that prototypes and their weights can be trained
simultaneously by General Loss Minimization (Sato,
2010), which is a generalized version of learning cri-
terion used in GLVQ. Experimental results for UCI
machine learning repository (Blake and Merz, 1998)
151
Sato A. and Ishii M. (2013).
Inverse of Lorentzian Mixture for Simultaneous Training of Prototypes and Weights.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 151-158
DOI: 10.5220/0004240201510158
Copyright
c
SciTePress

reveal that the proposed method achieves almost the
same as or higher classification accuracy than SVM,
while the number of prototypes is much less than that
of support vectors.
2 PROPOSED METHOD
2.1 Inverse of Lorentzian Mixture
Lorentzian, which is also known as Cauchy-
distribution, has the probability density function
p(x) =
1
π
γ
(x− y)
2
+ γ
2
, (1)
where y is the peak location and γ is the half-width
at half-maximum. Then, the discriminant function
for class ω
k
using the mixture of Lorentzian in d-
dimensional space can be written as
g
k
(x) =
m
k
∑
i=1
α
ki
γ
ki
kx− y
ki
k
2
+ γ
2
ki
, (2)
where α
ki
≥ 0 is a weight for the i-th distribution, and
y
ki
’s (i = 1, ··· ,m
k
) are regarded as prototypes. As-
suming that α
ki
γ
ki
= 1, we can obtain a more simple
form
g
k
(x) =
m
k
∑
i=1
1
kx− y
ki
k
2
+ b
ki
2
, (3)
where 1/α
ki
is replaced by b
ki
for ease of description.
As shown in Fig. 1, the height (or weight) of each dis-
tribution in Eq. (3) is defined only by the bias b
ki
, so
the above assumption is found to be useful for simpli-
fying the mixture of Lorentzian.
Let us consider the dissimilarity form by taking
the multiplicative inverse of Eq. (3) as follows:
d
k
(x) =
1
g
k
(x)
=
"
m
k
∑
i=1
kx− y
ki
k
2
+ b
2
ki
p
#
1/p
, (4)
where p = −1. Since this equation is formulated by
using L
p
norm, we can extend it by taking appropri-
ate value for p < 0. For example, when p → −∞, we
can obtain the nearest neighbor rule using biased Eu-
clidean distance as follow:
lim
p→−∞
d
k
(x) =
m
k
min
i=1
kx− y
ki
k
2
+ b
2
ki
. (5)
Therefore, Eq. (4) can be regarded as a natural exten-
sion of the conventional nearest neighbor rule. If we
use (d+1)-dimensionalvectors defined by X← (x,0)
and Y
ki
← (y
ki
,b
ki
), Eq. (4) can be rewritten as
d
k
(X;θ) =
"
m
k
∑
i=1
kX− Y
ki
k
2
p
#
1/p
, (6)
0
0.2
0.4
0.6
0.8
1
-10 -5 0 5 10
x
1/(x*x+1)
1/(x*x+2)
1/(x*x+4)
1/(x*x+8)
Figure 1: Examples of Lorentzian using different values
for the bias. As the bias becomes larger, the height of the
Lorentzian becomes lower.
where θ = {Y
ki
|k = 1,··· , K;i = 1,· ·· ,m
k
} denotes
a set of classifier parameters. Therefore, to train the
(d + 1)-dimensional vectors {Y
ki
} is to train both the
prototypes and ther biases, simultaneously.
2.2 Learning based on GLM
To estimate the values of classifier parameters, Gen-
eral Loss Minimization (GLM) is employed, because
it is a general framework for classifier design (Sato,
2010). GLM can deal with prior probabilities and
various losses as well as zero-one loss for multi-class
classification problems, but more simplified form is
used in this paper. Employing zero-one loss and as-
suming that the prior probabilities are proportional to
the number of samples in each class, the total loss can
be written as follows:
L(θ) =
1
N
N
∑
n=1
K
∑
k=1
K
∑
j6=k
f(ρ
kj
(x
n
;θ))1(t
n
= ω
k
). (7)
where θ is a set of classifier parameters, N is the num-
ber of training samples, K is the number of classes, x
n
is the n-th training sample, t
n
is the genuine class of
x
n
, ω
k
is the k-th class, and 1(·) denotes an indica-
tor function such that 1(true) = 1 and 1( false) = 0.
f(ρ
kj
(·)) is a sort of a risk associated with assigning
x
n
to class ω
j
, and ρ
kj
(·) is the misclassification mea-
sure of x
n
defined by
ρ
kj
(x
n
;θ) =
d
k
(x
n
;θ) − d
j
(x
n
;θ)
d
k
(x
n
;θ) + d
j
(x
n
;θ)
, (8)
where d
k
(·) and d
j
(·) are dissimilarity-based discrim-
inant functions of class ω
k
and class ω
j
, respectively,
having positive values. The value of ρ
kj
(·) ranges be-
tween −1 and 1, and leads to a correct (wrong) de-
cision when it is negative (positive.) In other words,
if ρ
kj
(·) is positive, we can know that x
n
falls into
a wrong decision region. The function f(·) is a loss
function with respect to the misclassification measure.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
152

In this paper, the following semi-sigmoid function
is used, because it resembles the hinge loss used in
SVM:
f(ρ) =
1
1+ exp(−ξρ)
for ρ < 0,
(ξρ+ 2)/4 for ρ ≥ 0.
(9)
Since the slant of the loss function ξ(> 0) defines the
margin between classes, we have to tune it with care
(Sato, 2010).
In GLM, the classifier parameters are estimated
by minimizing L(θ) based on gradient search. If we
employ the steepest descent method, θ is updated it-
eratively (t ← t + 1) as
θ
(t+1)
= θ
(t)
+ ∆θ
(t)
, ∆θ
(t)
= −ε(t)
∂L(θ)
∂θ
θ=θ
(t)
(10)
until θ
(t+1)
≃ θ
(t)
, where ε(t) > 0 and t denotes time.
The differential of L(θ) can be derived as
∂L(θ)
∂θ
=
1
N
N
∑
n=1
K
∑
k=1
K
∑
j6=k
f
′
(ρ
kj
(x
n
;θ))
×
∂ρ
kj
(x
n
;θ)
∂θ
1(t
n
= ω
k
), (11)
where f
′
(·) denotes the differential of f(·) as follows:
f
′
(ρ) =
(
ξf(ρ)(1− f(ρ)) for ρ < 0,
ξ/4 for ρ ≥ 0.
(12)
Here, let us use (d+ 1)-dimensional vectors as shown
in Eq. (6). The differentiation of ρ
kj
(·) in Eq. (11)
depends on the class to which the prototype belongs.
For Y
ki
which belongs to the correct class ω
k
,
∂ρ
kj
(X
n
;θ)
∂Y
ki
=
−4d
j
(X
n
;θ)
[d
k
(X
n
;θ) + d
j
(X
n
;θ)]
2
×
d
k
(X
n
;θ)
kX
n
− Y
ki
k
2
1−p
(X
n
− Y
ki
), (13)
and for Y
ji
which belongs to the wrong class ω
j
,
∂ρ
kj
(X
n
;θ)
∂Y
ji
=
4d
k
(X
n
;θ)
[d
k
(X
n
;θ) + d
j
(X
n
;θ)]
2
×
d
j
(X
n
;θ)
kX
n
− Y
ji
k
2
1−p
(X
n
− Y
ji
). (14)
Therefore, the update rules are obtained by substitut-
ing θ ← Y
ki
or θ ← Y
ji
in Eq. (10). In practice, the
conjugate gradient method is used for optimizing the
parameters. Note that we can obtain the prototypes
and the biases which minimize the total loss, simulta-
neously, because Y
ki
consists of y
ki
and b
ki
. In the ex-
periments, the initial values of the prototypes were de-
termined by using K-means algorithm for each class.
For the biases, the same value was assigned to each
before learning, and they were normalized to satisfy
the following constraint during learning, so that the
biases range within a limit:
K
∑
k=1
m
k
∑
i=1
b
2
ki
= C
2
. (15)
The outline of the learning algorithm is summarized
in Algorithm I.
Algorithm 1: Learning of the proposed method.
INPUT: p, ξ, C, m
k
(k = 1,··· , K)
INITIALIZE: y
ki
← K-means, b
ki
= C
p
∑
k
m
k
(i = 1,··· ,m
k
;k = 1,··· , K)
while not converged do
· θ
(t+1)
= θ
(t)
+ ∆θ
(t)
, where L(θ
(t+1)
) ≤ L(θ
(t)
)
· b
ki
← b
ki
×C
.
q
∑
k
∑
i
b
2
ki
(i = 1,··· ,m
k
;k = 1,··· , K)
end while
OUTPUT: y
ki
, b
ki
(i = 1,· ·· ,m
k
;k = 1,· ·· ,K)
3 EXPERIMENTS
To demonstrate the effectiveness of the proposed
method, hereinafter referred to as ILM, two kinds
of experiments were conducted: one was for two-
dimensional artificial data, and the other was for the
UCI machine learning repository.
3.1 Preliminary Experiments
Preliminary experiments for two-class two-
dimensional artificial data were conducted to
evaluate the effects of hyperparameters in ILM.
Figure 2 shows examples of decision boundaries
using different values for p in Eq. (6) and C in
Eq. (15). Prototypes are shown by white circles, and
the same value is assigned to every bias in each figure
according to the constraint of Eq. (15). As the value
of p becomes smaller, the decision boundaries tend to
approximate Voronoi diagrams, because the decision
rule becomes similar to the nearest neighbor rule.
While, as the value of C becomes larger, they tend
to form more simple shapes, because the Euclidean
distance between a sample and a prototype becomes
to have a larger bias.
Figure 3 shows the decision boundaries after
learning by ILM. Cross and plus marks denote train-
ing samples for each class, and white circles denote
prototypes. Each figure corresponds to that shown
in the bottom row in Fig. 2, which was used as the
InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights
153

p = −1 p = −2 p = −4 p = −8
C = 0.0
C = 1.0
Figure 2: Examples of decision boundaries for two classes using different values for p and C in the proposed method.
Prototypes are shown by white circles, and the same value is assigned to every bias in each figure according to the constraint
of Eq. (15).
p = −1 p = −2 p = −4 p = −8
C = 1.0
Figure 3: Decision boundaries after learning by the proposed method. Cross and plus marks denote training samples for each
class, and white circles denote prototypes. Each figure corresponds to that shown in the bottom row in Fig. 2, which is the
initial state before learning.
0.001
0.01
0.1
1
1 2 3 4 5 6 7
Bias
Prototypes
p=-1
1 2 3 4 5 6 7
Prototypes
p=-2
1 2 3 4 5 6 7
Prototypes
p=-4
1 2 3 4 5 6 7
Prototypes
p=-8
Figure 4: The values of biases after learning, sorted in as-
cending order. Each graph corresponds to the result shown
in Fig. 3.
initial state before learning. Note that all training
samples were used as initial values of prototypes in
these experiments. As shown in the figures, the pro-
totypes which belongs to the blue class become closer
each other as p becomes smaller, and the decision
boundary tends to maximize the margin between the
two classes after learning. Therefore, ILM trained by
GLM can be regarded as a maximal margin classi-
fier as discussed in the literature (Sato, 2010). Fig-
ure 4 shows the values of biases after learning. Each
graph corresponds to the result shown in Fig. 3. Since
the bias is defined as the reciprocal of the weight
for Lorentzian, the smaller biases are more important
than larger ones, and the prototypes having larger bi-
ases can be removed. For example, the top three can
be removed for p = −1, and the top two can be re-
moved for p < −1. The decision boundaries after re-
moval were almost the same as shown in Fig. 3. Since
no difference was found to the eye, the figures after
removal are not shown in this paper.
3.2 UCI Machine Learning Repository
3.2.1 Experimental Setup
Experiments for the UCI machine learning repository
were conducted to evaluate the performance of ILM.
Some data preprocessing was employed beforehand
as used in the literatures (Meyer et al., 2003): 1) all
records containing any missing values were removed
from the dataset, 2) a binary coding scheme was used
for handling categorical variables, and 3) all metric
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
154

Table 1: Experimental results for UCI machine learning repository. “Ins.” denotes the number of instances after removing
missing data, “Att.” denotes the number of attributes excluding class attribute, and “#” denotes the number of support vectors
or prototypes. The proposed method, referred to as ILM, was evaluated with different parameter sets: some parameters were
fixed as (a) C = 0, p = −2
8
, (b) C = 0, (c) p = −1, and the other parameters were varied.
SVM ILM
Dataset Ins. Att. (a) (b) (c)
Error # Error # Error # Error #
(%) (%) (%) (%)
BreastCancer 683 9 2.8 61 2.3 4 2.2 4 2.3 64
Cards 653 15 12.9 218 12.6 4 12.4 4 12.3 8
Heart1 297 13 14.1 139 13.5 8 13.5 8 13.1 2
HouseVotes84 435 16 3.7 102 3.7 2 3.4 8 3.2 4
Ionosphere 351 34 4.3 149 6.8 32 3.4 16 3.1 16
Liver 345 6 27.0 211 28.1 4 26.4 4 24.9 8
P.I. Diabetes 768 8 22.3 423 21.9 2 21.6 4 21.6 4
Sonar 208 60 11.5 154 8.7 32 7.7 32 11.1 8
Tictactoe 958 9 1.5 813 0.2 16 0.2 16 1.5 16
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
m=1 m=2 m=4
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
m=8 m=16 m=32
Figure 5: Error rates for BreastCancer in UCI machine learning repository by the proposed method with parameter set (c).
variables were scaled to zero mean and unit variance.
Nine datasets
1
as shown in Table 1 were evaluated
based on 10-fold cross validation. That is to say, the
data were divided into 10 partitions, and 9 partitions
were used for training and the rest was used for test-
ing. This process was then repeated 10 times, and
the obtained results were averaged to produce a single
estimation. All of the datasets are two-class classifi-
1
The actual names in UCI machine learning reposi-
tory are Breast Cancer Wisconsin (Original), Credit Ap-
proval, Heart Disease, Congressional Voting Records, Iono-
sphere, Liver Disorders, Pima Indians Diabetes, Connec-
tionist Bench (Sonar, Mines vs. Rocks), Tic-Tac-Toe
Endgame, respectively.
cation problems, so that we can compare the perfor-
mance of ILM with SVM.
The proposed method has several hyperparame-
ters: p and m
k
in Eq. (6), C in Eq. (15), and ξ in
Eq. (9). In the experiments, the same number given
by m was used for m
k
(k = 1, ··· , K), so the per-
formance was evaluated using different values for p,
C, m and ξ. Specifically, p = {−2
i
|i = 0,· ·· ,8},
C = {0,2
i
|i = 0,· ·· ,10}, m = {2
i
|i = 0,· ·· ,5}, and
ξ = {2
i
|i = 1,· ·· ,8} were used.
InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights
155

0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
BreastCancer (m=32) Cards (m=4) Heart1 (m=1)
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
HouseVotes84 (m=2) Ionosphere (m=8) Liver (m=4)
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
ξ=2
ξ=4
ξ=8
ξ=16
ξ=32
ξ=64
ξ=128
ξ=256
0
10
20
30
40
50
1 10 100 1000
Error (%)
Normalization Value for Bias
xi=2
xi=4
xi=8
xi=16
xi=32
xi=64
xi=128
xi=256
P.I.Diabetes (m=2) Sonar (m=4) Tictactoe (m=8)
Figure 6: Error rates for UCI machine learning repository by the proposed method with parameter set (c).
3.2.2 Experiment I
Results by ILM are shown in Table 1. The lowest er-
ror rates are listed for different parameter set: some
parameters were fixed as (a) C = 0, p = −2
8
, (b)
C = 0, (c) p = −1, and the other parameters were var-
ied. Set (a) corresponds to GLVQ (p → −∞), set (b)
corresponds to an extension of GLVQ using L
p
norm-
based mixture, and set (c) corresponds to the multi-
plicative inverse of the linear mixture of Lorentzian.
Overall, the classification accuracy for set (c) is bet-
ter than set (a) and set (b), except Sonar and Tictac-
toe. This means that the learning of biases is very ef-
fective to improve classification accuracy, while the
L
p
norm-based mixture is also important for some
datasets. Figure 5 shows the error rates for Breast-
Cancer by ILM with set (c). The horizontal axis de-
notes the value of C, and the error rates using differ-
ent values for ξ are shown. It is noteworthy that the
lowest error in each figure is not so different. This
means that ILM does not seem to suffer from the over-
fitting even though many prototypes are used. Fig-
ure 6 shows similar graphs to Fig. 5, but the best result
in various m was selected for each dataset. Note that
the number of prototypes by ILM as shown in Table 1
is just twice as many as the selected m.
Similar experiments by SVM were conducted for
comparison. Actually, SVM
light
was used for evalua-
tion. The hyperparametersin SVM are the trade-offC
and RBF parameter γ in K(x, y) = exp(−γkx− yk
2
).
The performance was evaluated using different values
for C and γ. Specifically, C = {2
i
|i = −5, ···12} and
γ = {2
i
|i = −10,··· ,5} were used. The lowest error
rates and the number of the obtained support vectors
are listed in Table 1. Clearly, the error rates by ILM
are lower than those by SVM, while the number of
prototypes is much less than that of support vectors.
For BreastCancer, the number of prototypes by ILM
(c) listed in the table is larger than that of support vec-
tors, but the error rates stayed lower even though a
fewer prototypes were used. For example, it was 2.6
(%) for two prototypes (i.e. m = 1). Figure 7 shows
the results by SVM. These graphs are similar to Fig. 6,
but the horizontal axis denotes log
2
C, and the error
rates using different values for RBF parameter γ are
shown.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
156

0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
BreastCancer Cards Heart1
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
HouseVotes84 Ionosphere Liver
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
0
10
20
30
40
50
-5 0 5 10 15
Error (%)
log2(C)
-10
-9
-8
-7
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
P.I.Diabetes Sonar Tictactoe
Figure 7: Error rates for UCI machine learning repository by SVM with RBF kernel.
3.2.3 Experiment II
The results in Table 1 show that the proposed method
has capability to improve classification accuracy for
any datasets used in the experiments. However, in
practice, the hyperparameters should be estimated
without testing data. Table 2 shows similar experi-
mental results for UCI machine learning repository,
but the hyperparameters in ILM and SVM were tuned
with only training data through two-fold cross valida-
tion. Of course, the error rates are slightly worse than
those in Table 1, but ILM retains almost the same as
or better performance than SVM on the whole.
4 DISCUSSION
Experimental results for UCI machine learning repos-
itory revealedthat ILM achievesalmost the same as or
higher classification accuracy than SVM with a much
fewer prototypes than support vectors. The main ad-
vantage of ILM seems to train prototypes as well as
biases (or weights), while only weights are trained in
SVM. This may lead to reducing the number of pro-
totypes for achieving good performance. Since the
training of prototypes needs distance calculation at
every iteration in gradient search, it results in time
consumption as increasing the number of samples or
prototypes, or the dimensionality. In addition, the cost
function defined by Eq. (7) does not seem to ensure
the convexity. However, as shown in the experiments,
ILM gives a good performance for real datasets, so
it can become one of the powerful methods for clas-
sification. It was also shown that prototypes having
larger biases can be removed without degrading per-
formance in the preliminary experiments, but this re-
dundancy removal should be investigated further.
5 CONCLUSIONS
A novel distance-based classifier based on the multi-
plicative inverse of Lorentzian mixture was proposed,
which can be regarded as a natural extension of the
InverseofLorentzianMixtureforSimultaneousTrainingofPrototypesandWeights
157
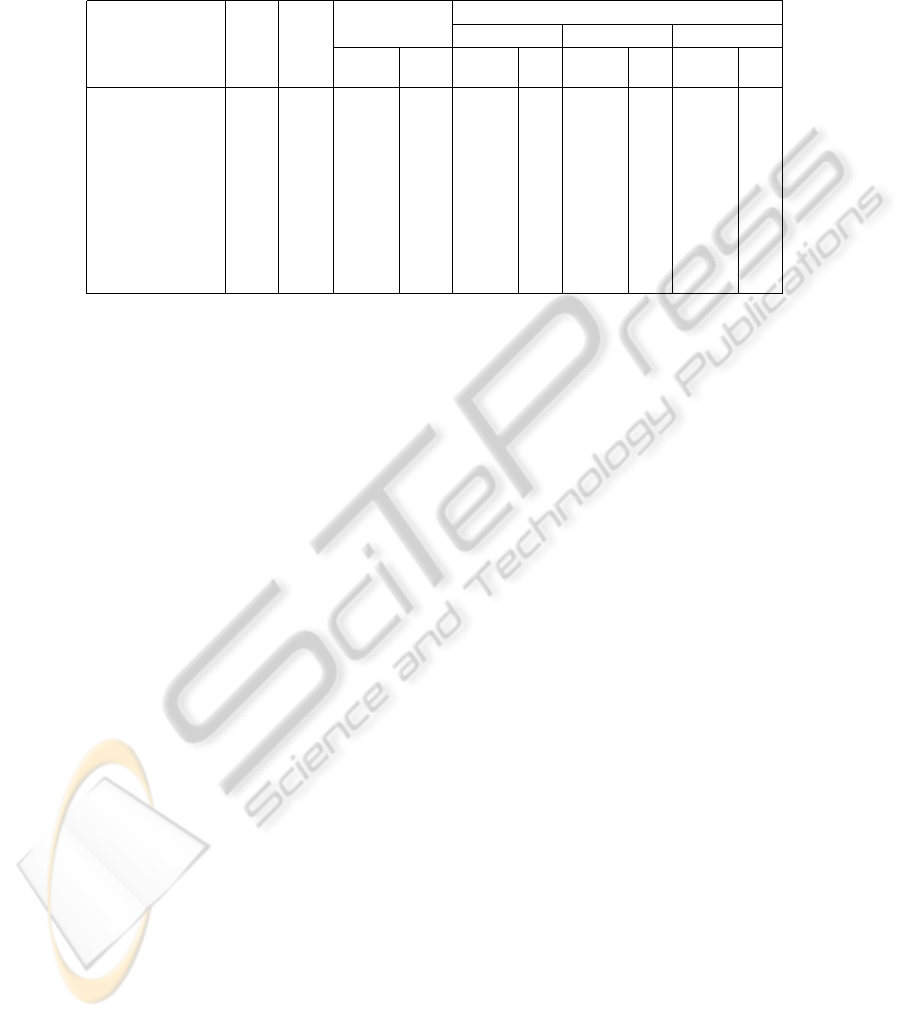
Table 2: Experimental results for UCI machine learning repository. Hyperparameters were tuned with only training data
through cross validation. “Ins.” denotes the number of instances after removing missing data. “Att.” denotes the number
of attributes excluding class attribute, and “#” denotes the number of support vectors or prototypes. The proposed method,
referred to as ILM, was evaluated with different parameter sets: some parameters were fixed as (a)C = 0, p = −2
8
, (b)C = 0,
(c) p = −1, and the other parameters were varied like in Table 1.
SVM ILM
Dataset Ins. Att. (a) (b) (c)
Error # Error # Error # Error #
(%) (%) (%) (%)
BreastCancer 683 9 2.8 66 2.5 32 2.6 64 2.6 64
Cards 653 15 13.6 189 13.2 8 13.9 8 14.6 4
Heart1 297 13 14.5 159 16.5 2 18.2 64 14.8 2
HouseVotes84 435 16 3.7 101 3.7 2 3.9 16 3.7 32
Ionosphere 351 34 4.8 148 8.3 8 3.7 32 4.3 64
Liver 345 6 28.1 203 28.1 4 27.5 4 26.3 4
P.I. Diabetes 768 8 22.3 418 22.5 2 22.3 32 21.9 64
Sonar 208 60 12.1 125 11.1 16 9.6 8 11.5 16
Tictactoe 958 9 1.7 349 1.7 2 0.9 16 1.7 2
conventional nearest neighbor rule. It was shown that
prototypes and biases can be trained simultaneously
by General Loss Minimization, which is a general
framework for classifier design. The preliminary ex-
periments raised the possibility that prototypes having
larger biases can be removed without degrading per-
formance, but this redundancy removal should be in-
vestigated further. Experimental results for UCI ma-
chine learning repository revealed that the proposed
method achieves almost the same as or higher clas-
sification accuracy than SVM for all of nine datasets
with a much fewer prototypes than support vectors.
In future, the proposed method will be evaluated for
various classification problems in real world.
REFERENCES
Blake, C. and Merz, C. (1998). UCI repository of machine
learning databases. University of California, Irvine,
Dept. of Information and Computer Sciences.
Cortes, C. and Vapnik, V. (1995). Support vector networks.
Machine Learning, 20:273–297.
Crammer, K., Gilad-Bachrach, R., Navot, A., and Tishby,
N. (2003). Margin analysis of the lvq algorithm. In
Advances in Neural Information Processing Systems,
volume 15, pages 462–469. MIT Press.
Giraud, B. G., Lapedes, A. S., Liu, L. C., and Lemm, J. C.
(1995). Lorentzian neural nets. Neural Networks,
8(5):757–767.
Grbovic, M. and Vucetic, S. (2009). Learning vector
quantization with adaptive prototype addition and re-
moval. In International Conference on Neural Net-
works, pages 994–1001.
Hammer, B. and Villmann, T. (2002). Generalized rele-
vance learning vector quantization. Neural Networks,
15(8–9):1059–1068.
Karayiannis, N. (1996). Weighted fuzzy learning vec-
tor quantization and weighted generalized fuzzy c-
means algorithm. In IEEE International Conference
on Fuzzy Systems, pages 773–779.
Kohonen, T. (1995). Self-Organizing Maps. Springer-
Verlag.
Meyer, D., Leisch, F., and Hornik, K. (2003). The support
vector machine under test. Neurocomputing, 55(1–
2):169–186.
Qin, A. K. and Suganthan, P. N. (2004). A novel ker-
nel prototype-based learning algorithm. In Inter-
national Conference on Pattern Recognition (ICPR),
pages 621–624.
Sato, A. (1998). A formulation of learning vector quantiza-
tion using a new misclassification measure. In the 14th
International Conference on Pattern Recognition, vol-
ume 1, pages 322–325.
Sato, A. (2010). A new learning formulation for kernel clas-
sifier design. In International Conference on Pattern
Recognition (ICPR), pages 2897–2900.
Sato, A. and Yamada, K. (1996). Generalized learning vec-
tor quantization. In Advances in Neural Information
Processing Systems, volume 8, pages 423–429. MIT
Press.
Schneider, P., Biehl, M., and Hammer, B. (2009). Adap-
tive relevance matrices in learning vector quantiza-
tion. Neural Computation, 21(12):3532–3561.
Villmann, T. and Haase, S. (2011). Divergence-based vector
quantization. Neural Computation, 23(5):1343–1392.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
158
