
An Efficient Translation Scheme for Representing Nurse Rostering
Problems as Satisfiability Problems
Stefaan Haspeslagh
1
, Tommy Messelis
1
, Greet Vanden Berghe
2
and Patrick De Causmaecker
1,2
1
CODeS (member of ITEC-IBBT-KU Leuven), Department of Computer Science, KU Leuven KULAK,
E. Sabbelaan 53, 8500 Kortrijk, Belgium
2
CODeS, Vakgroep IT, KAHO, Gebr. De Smetstraat 1, 9000 Gent, Belgium
Keywords:
Nurse Rostering, Satisfiability Problems, Automated Translation, Counting Constraints.
Abstract:
In this paper we present efficient translation schemes for converting nurse rostering problem instances into
satisfiability problems (SAT). We define eight generic constraints types allowing the representation of a large
number of nurse rostering constraints commonly found in literature. For each of the generic constraint types,
we present efficient translation schemes to SAT. Special attention is paid to the representation of counting
constraints. We developed a two way translation scheme for counting constraints using O(nlogn) variables
and O(n
2
) clauses. We translated the instances of the First international nurse rostering competition 2010 to
SAT and proved the infeasibility of the instances. The SAT translation was used for a hardness study of nurse
rostering problem instances based on SAT features.
1 INTRODUCTION
We present schemes for automatically translating
nurse rostering problem instances into satisfiability
problem instances (SAT).
The SAT-translation scheme was originally de-
signed for a hardness study of nurse rostering prob-
lem instances (Bilgin et al., 2009). Some algorithms
perform well on some specific instances while those
same algorithms perform worse on others. (Leyton-
Brown et al., 2006) present an experimental approach
for predicting the running time of algorithms designed
to solve the winner determination problem for combi-
natorial auctions. The previous strategy was applied
to the more abstract problem of propositional satisfi-
ability (Nudelman et al., 2004) introducing a set of
91 features for the runtime prediction of several algo-
rithms that prove whether a certain problem instance
is satisfiable or not. This work has led to the construc-
tion of SATzilla, a portfolio solver for SAT problems
(Xu et al., 2008). This portfolio was very success-
ful, winning several tracks of different SAT competi-
tions
1
. The aforementioned SAT-features set is used
to predict the runtime of a certain algorithm and the
value of the objective function obtained by the algo-
rithm.
1
More information about these competitions can be
found at http://www.satcompetition.org
A second potential application of the SAT transla-
tion scheme is applying SAT (or MaxSAT) solvers to
nurse rostering problem instances. As a first attempt,
(Acharyya, 2008) translates a simple nurse rostering
problem with a small set of constraints into SAT and
applies GSAT to solve it. The approach is limited
to small instances as the number of clauses increases
rapidly with the size of the instances. It is thus impor-
tant to develop efficient encodings of the constraints.
Modeling optimisation problems involving con-
straints on sequences of decision variables to mixed
integer programs (and SAT) can be very complex
(C
ˆ
ot
´
e et al., 2011). Special attention is given to the
translation of counting constraints into SAT clauses.
We present an efficient translation procedure generat-
ing O(n
2
) clauses and O(nlogn) variables. (Bailleux
and Boufkhad, 2003) developed a translation scheme
with similar complexity. (Sinz, 2005) provides a
O(n.k) and (As
´
ın et al., 2009) a O(nlog
2
(k)) scheme
to translate the constraint x
1
+...+x
n
≤ k. All contri-
butions however, only provide a one way translation,
preserving arc consistency. As for the hardness stud-
ies, we do not solely focus on solving nurse rostering
problems using SAT, a two way translation was re-
quired.
(Cadoli and Schaerf, 2005) present the automated
translation of problem specifications expressed in NP-
SEC into SAT. NP-SEC in a logic based language ca-
303
Haspeslagh S., Messelis T., Vanden Berghe G. and De Causmaecker P..
An Efficient Translation Scheme for Representing Nurse Rostering Problems as Satisfiability Problems.
DOI: 10.5220/0004259103030310
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 303-310
ISBN: 978-989-8565-39-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

pable of expressing all problems belonging to com-
plexity class NP. The authors tested the system on a
few classical problems such as graph colouring and
job-shop scheduling, NP-complete problems with a
rather simple problem definition. The authors high-
light the benefits of an automated approach. Although
the performance of SAT solvers on the generated in-
stances is often inferior to manual encodings, the au-
thors stem that the system is a valuable tool for devel-
oping fast prototypes for new problems, or variations
of known ones for which no specific solver is avail-
able.
In Section 2, an abstract respresentation of
nurse rostering problems using numberings is de-
scribed. Section 3 elaborates on the formal defini-
tion of generic constraints types. In Section 4, each
generic constraint type is translated to SAT. Section 5
demonstrates the applicability of the SAT translation
schemes for a hardness study of nurse rostering prob-
lem instances. Section 6 concludes and gives direc-
tions for further research.
2 ABSTRACT REPRESENTATION
OF NURSE ROSTERING
PROBLEMS USING
NUMBERINGS
The nurse rostering problem under study is the prob-
lem presented in the First international nurse rostering
competition (Haspeslagh et al., 2012). The authors
used numberings, originally designed for the efficient
evaluation of constraint violations (Burke et al., 2001)
as an abstract representation of constraints. After we
elaborate on the definition of numberings, we give an
example numbering for some sample constraints. For
a full description of the competition’s constraint, we
refer to the original paper.
2.1 Numberings
We start with some elementary notation.
Definition 1. A time unit is an elementary interval of
time in which a nurse can be assigned a shift.
In our case, shift types determine those intervals.
So, each shift type has a corresponding time unit. In
the case of the nurse rostering problems considered
within this paper, the number of time units equalled
the number of shift types times the number of days
in the planning period. Thus, supposing we have a
planning horizon of D days and for each day there are
Sh shift types, we have a set T of D ∗ Sh time units.
A solution to a nurse rostering problem is then an as-
signment of nurses to shifts on specific time units.
Numberings on the time units are defined as fol-
lows:
Definition 2. A numbering N
i
is a mapping of the
set of time units onto a set of numbers extended
with the symbol U i.e. N
i
: T → {−M,−M +
1,...,0,1,...,M − 1,M,U } where i = 1,...,I and I
is the total number of numberings. M is a positive
integer and U (undefined) is a symbol introduced to
represent the time units that are not mapped onto a
number.
The mapping does not need to be into or onto, nor
does it need to preserve sequence. An event is a time
unit for which a nurse has a shift type assigned. The
idea of the evaluation method (Burke et al., 2001) is
to go through the set of events for which the time units
do not have U (undefined) as value. We call these the
’numbered events’. More formally:
Definition 3. A personal schedule S
p
for person p is
a mapping S
p
: T → {working,free}.
Definition 4. For a given personal schedule S
p
an
event is a time unit e for which S
p
(e) = working.
Denote by T
S
p
the set of all time units for which
S
p
maps to working. T
S
p
is thus the set of time units
induced by S
p
, or in other words: the set of time units
for which nurse p is assigned to work. Denote by T
N
i
the set of time units for which the numbering N
i
is
defined.
Definition 5. The event set T
S
p
,N
i
:= T
S
p
∩ T
N
i
is the
set of time units induced by the schedule S
p
, for which
the numbering N
i
is defined (6= U).
Definition 6. Two events e
j
and e
j+1
are consecutive
with respect to numbering N
i
if N
i
(e
j+1
) − N
i
(e
j
) = 1
We can now express the following four groups of
constraints:
• total number of assignments (total): for a num-
bering N
i
, this constraint type limits the number
of events e for which N
i
(e) 6= U.
• total number of assignments of a certain type (per-
Type): for a numbering N
i
, this constraint type
limits the number of events corresponding to a
specific number j (N
i
(e) = j).
• consecutive assignments (consecutiveness): for a
numbering N
i
, this constraint limits the length a a
sequence of consecutive events in T
S
p
,N
i
.
• gaps between consecutive sequences of assign-
ments (between): for a numbering N
i
this con-
straint type limits the maximum gap (e.g. free
time) between two non-consecutive events e
j
and
e
j+1
(the gap equals N
i
(e
j+1
) − N
i
(e
j
)).
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
304

Table 1: Example numbering.
Day Mo Tu We Th Fr
ST E L E L E L E L E L
T 0 1 2 3 4 5 6 7 8 9
N 0 0 1 1 2 2 3 3 4 4
E ∗ ∗ ∗ ∗
cons 1 1 1 2 2 3 0 0 1 1
last 1 1 1 2 2 3 3 3 4 4
For each constraint type, a maximum and min-
imum bound can be set: max total and min total,
max consecutive and min consecutive, max between
and min between and max pert and min pert.
Four counting variables are introduced. total rep-
resents the total number of events for the number-
ing. consecutive represents the number of consecutive
events. If an interruption in a sequence is found, the
counter is reset to 0. pert keeps track of the number
of events per value in the numbering and last keeps
track of the number of the last evaluated event.
With each numbering N
i
a set of four of the above
counters is associated. During the evaluation, by com-
paring the counter with one of the abovementioned
constraint types, constraint violations are detected.
An example for a simplified nurse rostering prob-
lem with two shift types (ST) is given in Ta-
ble 1. We want to evaluate two constraints: the em-
ployee should work at most two consecutive days
(max consecutive = 2) and should have at least two
consecutive days off (min between = 2). E shows
the assignments to one employee. At time unit 5, a
first violation is detected as the value of the counter
cons exceeds max consecutive. At time unit 8, a sec-
ond violation is detected as (current number − last >
min between).
3 FORMAL DEFINITIONS OF
GENERIC CONSTRAINTS
In this study, we only consider monotonically ascend-
ing (Definition 7) numberings.
Definition 7. A numbering N
i
is monotonically as-
cending if, for every two time units j
a
and j
b
for which
N
i
is defined (6= U), j
a
< j
b
⇒ N
i
( j
a
) ≤ N
i
( j
b
).
The constraints on the numberings can be ex-
pressed using event sets. An important concept in
the expression of constraints is the notion of event
sequences, in particular sequences that increase at a
steady pace.
Definition 8. The event set E of a numbering N
i
and
a personal schedule S
p
is the set T
S
p
,N
i
.
With every event e ∈ E, a unique number (∈ N
i
) is
associated. We refer to Section 2.1 for detailed infor-
mation on the definition of S
p
and T
S
p
,N
i
.
Definition 9. An event sequence r is any sequence of
events e
j
from E, ( j = 0 ...m), conserving the order
of the time units corresponding to the events.
Definition 10. A sequence r is contiguously ascend-
ing if ∀ j ∈ {1, . . . , m} : e
j
− e
j−1
= 1.
We can now give formal definitions for the con-
straints in Table 2. Note that the subject of these
constraints is depending on the numbering. All con-
straints of the competition’s instances can be de-
scribed using monotonically ascending numberings
and are of one of the presented constraint types.
Table 2: Formal definition of eight generic constraints.
Constraint Value Definition
max consecutive max
c
There is no contiguously ascending event se-
quence of length max
c
+ 1
min consecutive min
c
There is no contiguously ascending event se-
quence of length l: min
c
> l ≥ 1 which is not
part of another ascending event sequence of
length at least min
c
.
max between max
b
For any two consecutive events e
j
and e
j+1
,
N
i
(e
j+1
) − N
i
(e
j
) ≤ max
b
min between min
b
For any two consecutive events e
j
and e
j+1
,
N
i
(e
j+1
) − N
i
(e
j
) ≤ 1 or N
i
(e
j+1
) − N
i
(e
j
) ≥
min
b
max total max
t
The event set E contains at most max
t
events
min total min
t
The event set E contains at least min
t
events
max perType(i) max
pt
The event set E contains at most max
pt
events
corrensponding to a number k
min perType(i) min
pt
If the event set E contains an event correspond-
ing to a number k, then it contains at least min
pt
events corresponding to k
4 TRANSLATION OF GENERIC
CONSTRAINTS TO SAT
We present a scheme to translate each of the eight
generic constraints from Section 3 to Conjunctive
Normal Form SAT clauses (Cook, 1971). A prepro-
cessing step is performed before the translation of the
constraint types.
4.1 Preprocessing
We introduce boolean decision variables v
p, j
indicat-
ing whether nurse p is working time unit j. Since the
expression of the sequence constraints is basically the
same for all employees, we denote v
p, j
as v
j
, in order
to simplify the notation.
For some numberings, consecutive time units are
assigned the same number, e.g. the example number-
ing N in Table 1 does not distinguish between dif-
ferent shifts on the same day. Hence it is natural to
introduce a variable t
i
indicating for each sequence of
consecutive time units with equal numbers whether
an employee is working on a time unit within that se-
quence. Generally, for such a sequence of time units
starting at k and ending at l:
AnEfficientTranslationSchemeforRepresentingNurseRosteringProblemsasSatisfiabilityProblems
305

Table 3: Preprocessing for ’between’ constraints.
Time unit 1 2 3 4 - - 5 6
Numbering 1 1 2 2 - - 5 5
Variable v
1
v
2
v
3
v
4
- - v
5
v
6
Preprocessing t
1
t
2
t
3
t
4
t
5
t
i
⇔
l
_
j=k
v
j
or in cnf: ¬t
i
∨ (
l
_
j=k
v
j
) and
l
^
j=k
(t
i
∨ ¬v
j
)
This results in 2 + l − k clauses. For n numbers
in the numbering we generate at most dn/2e variables
and at most 1+dn/2e clauses. The preprocessing step
thus results in O(n) variables and O(n) clauses.
4.1.1 Preprocessing for between Constraints
Translating ’between’ constraints requires a slightly
different preprocessing step. Where a numbering is
interrupted, one or more implicit variables with value
’False’ should be placed. An example is given in
Table 3, both variables t
3
≡ False and t
4
≡ False.
Without the implicit variables, some event sequences
would lack. Suppose we want a gap of at most 1
between two consecutive events and an event occurs
for t
2
(v
3
= True or v
4
= True) and t
5
(v
5
= True or
v
6
= True). Between the two events, there is a gap of
2. By omitting the implicit variables, the two event
sequences detecting the violation would be missing.
The preprocessing step results in at most O(n) ex-
tra variables and as many extra clauses as variables
added.
4.2 Translation of ’Consecutive’ and
’between’ Constraints
4.2.1 Maximum Number of Consecutive Events
and Free Time Units between Two Events
As stated in Table 2 there should not be a contigu-
ously ascending event sequence of length max
c
+ 1.
For every contiguously ascending sequence cas (cas
i
is the index in the original sequence of the i
th
variable
within cas) we have the following clauses:
¬
max
c
^
j=0
t
cas
i
!
, in cnf:
max
c
_
i=0
(¬t
cas
i
)
Analogously, for a maximum gap between two events,
we obtain:
¬
max
b
^
j=0
¬t
cas
i
!
, in cnf:
max
b
_
i=0
(t
cas
i
)
In general, both constraints for a monotonically as-
cending numbering with n numbers generates at most
(n − max
c
), respectively (n − max
b
) clauses and no
extra variables.
4.2.2 Minimum Number of Consecutive Events
and Free Time Units between Two Events
Following Table 2, there should not be a contiguously
ascending event sequence of length l (min
c
> l > 1)
which is not part of another contiguously ascending
event sequence of length at least min
c
. This implies
that in any consecutive sequence of variables t
i
of
length l (min
c
+1 ≥ l ≥ 3) the middle variables cannot
be true without one of the border variables. For ev-
ery contiguously ascending sequence cas of length l
(3 ≤ l ≤ min
c
+1) this results in the following clauses:
¬
¬t
cas
0
∧ ¬t
cas
l−1
∧
l−2
^
i=1
t
cas
i
)
!!
,
in cnf: t
cas
0
∨t
cas
l−1
∨
l−2
_
i=1
¬t
cas
i
!
Analogously, for a minimum gap between two events,
we obtain:
¬
t
cas
0
∧t
cas
l−1
∧
l−2
^
i=1
¬t
cas
i
)
!!
,
in cnf: ¬t
cas
0
∨ ¬t
cas
l−1
∨
l−2
_
i=1
t
cas
i
!
In general, both constraints for a monotonically as-
cending numbering consisting of n numbers, generate
at most (n − min
c
) clauses and no extra variables.
4.3 Translation of Counting Constraints
We developed an efficient general procedure for trans-
lating counting constraints into CNF clauses. First we
elaborate on the procedure in general. Then we show
how to translate total and pert constraint types using
this procedure.
4.3.1 General Procedure
This procedure uses an iterative process of introduc-
ing variables and clauses. We start by some elemen-
tary definitions.
Definition 11. V is the set of variables v
i
for which
we want to count the number of variables that are as-
signed true.
Definition 12. U
α,β
is the set of indices (of time units)
k between α and β for which v
k
in V is assigned true.
Definition 13. F
α,β
is the set of indices (of time units)
k between α and β for which v
k
in V is assigned false.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
306

We then introduce the variables u
i
, respectively f
i
,
denoting whether there are at least i elements in the set
U
1,n
, respectively F
1,n
, with n the number of elements
in V :
u
i
⇔ |U
1,n
| ≥ i, f
i
⇔ |F
1,n
| ≥ i for i ∈ {1,...,n} (1)
More generally, we introduce the variables u
x,y,z
( f
x,y,z
) denoting whether there are at least z events in
the set U
x,y
(F
x,y
):
u
x,y,z
⇔ |U
x,y
| ≥ z and f
x,y,z
⇔ |F
x,y
| ≥ z (2)
In the remainder of this section, we only consider the
first equivalence in (2). As u
i
= u
1,n,i
, for representing
equivalence (1), we show we only need to translate:
u
1,n,i
⇒ |U
1,n
| ≥ i (3)
By contradiction, the other direction of the equiva-
lence is equivalent with
¬u
1,n,i
⇒ ¬(|U
1,n
| ≥ i) (4)
If no i variables may be assigned true, at least n −i+1
variables should be assigned f alse:
(|U
1,n
| < i) ⇔ (|F
1,n
| ≥ n − i + 1) ⇔ f
n−i+1
(5)
Using (5), implication (4) becomes:
f
n−i+1
⇒ |F
1,n
| ≥ n − i + 1 (6)
This can be translated in the same way as we translate
(3).
4.3.2 Translation of u
1,n,i
⇒ |U
1,n
| ≥ i
First we prove the following equivalence:
u
1,n,i
⇔ (u
1,
n
2
,k
∨ u
n
2
+1,n,l
) for k + l = i + 1.
Lemma 1. u
1,n,i
⇒ (u
1,
n
2
,k
∨u
n
2
+1,n,l
) for k + l = i +1
In words, when U
1,n
contains at least i elements, then
U
1,
n
2
contains at least k elements or U
n
2
+1,n
contains at
least l elements. We will prove this by contradiction.
Proof. Let k
0
be the number of elements in U
1,
n
2
and
l
0
the number of elements U
n
2
+1,n
, then i
0
= k
0
+ l
0
is
the number of elements in U
1,n
.
Suppose that the right part of the implication does not
hold, so we have k
0
< k and l
0
< l
( k
0
< k ) and ( l
0
< l )
⇔ ( k
0
≤ k − 1 ) and ( l
0
≤ l − 1 )
⇒ ( k
0
+ l
0
) ≤ ( k + l − 1 − 1 )
⇔ i
0
≤ ( i − 1 )
⇔ i
0
< i
which is per definition ¬u
1,n,i
and thus contradicts to
the left part of the implication.
Using the above lemma we can split up the event
sets and rewrite the definition of u
1,n,i
as:
u
1,n,i
⇒ (u
1,
n
2
,k
∨ u
n
2
+1,n,l
) for all k ≥ 0,l ≥ 0
s.t. k + l = i + 1,i ∈ {1,...,n}
This is equivalent to:
u
1,n,i
⇒
^
k,l
(u
1,
n
2
,k
∨ u
n
2
+1,n,l
) for all k ≥ 0,l ≥ 0
s.t. k + l = i + 1,i ∈ {1,...,n}
This implication is then formulated as a CNF formula:
^
k,l
(¬u
1,n,i
∨ u
1,
n
2
,k
∨ u
n
2
+1,n,l
) for all k ≥ 0,l ≥ 0
s.t. k + l = i + 1
Given the limitations we can find (i + 2) pairs of val-
ues for k and l. Hence we need a total of (i + 2)
clauses to represent this implication as a cnf formula.
This procedure essentially expresses the variable u
1,n,i
in terms of lower level variables u
1,
n
2
,k
and u
n
2
+1,n,l
.
We need 2(i + 2) lower level variables to represent
the clauses. We must note here that we do not always
need all of these lower level variables, indeed the vari-
ables u
1,
n
2
,z
and u
n
2
+1,n,z
with z > (
n
2
+1) will trivially
be false, since there can not be more than (
n
2
+ 1) in-
dices in the sets U
1,
n
2
or U
n
2
+1,n
. In general, a variable
u
x,y,z
with z > (y−x +1) will always be trivially false.
This brings the actual number of lower level to at most
2(
n
2
+ 1).
Generally, we need min((n + 2),2(i + 2)) lower
level variables. In the worst case, when i equals n,
this is (n + 2).
Whereas the original definition of u
i
used sets of
size n, we are now left with sets of size
n
2
. We repeat
this recursively until the sets are of size 1. The vari-
ables u
x,x,0
and u
x,x,1
then correspond to ¬v
x
and v
x
respectively.
The ‘left’ variables u
1,
n
2
,k
with different k will in
their turn all use the same lower level variables u
1,
n
4
,k
0
and u
n
4
+1,
n
2
,l
0
. This is similar for the ‘right’ variables.
The second iteration will thus introduce 2.(n/2 + 2)
lower level variables. The total process will ulti-
mately introduce the following number of lower level
variables, for 2
k
= n:
(n + 2) + 2(n/2 + 2) + ... + 2
k−1
(n/2
k−1
+ 2)
= (n + 2) + n + 4 + ... + n + 2n
which equals
(n + n + ··· + n) + 2(2
0
+ 2
1
+ 2
2
+ ··· + 2
k−1
)
with twice k = log
2
n terms
= nlog
2
n + Σ
k
i=1
(2
i
)
= nlog
2
n + 2n − 2
= O(nlogn + n)
= O(nlogn)
AnEfficientTranslationSchemeforRepresentingNurseRosteringProblemsasSatisfiabilityProblems
307

The first iteration introduces (i + 2) lower level
clauses. In the worst case i equals n, thus (n + 2)
clauses are introduced. In a formula, the set of k
and l variables will produce the following number of
clauses
bn/2c
∑
i=0
(i + 1) +
dn/2e
∑
i=0
(i + 1)
which is O(n
2
).
4.3.3 Translation of Total and perType
Constraints
For an employee p and numbering N
x
, the total con-
straints impose restrictions on the minimum and max-
imum number of decision variables v
p, j
(for which N
x
is defined) that can be assigned true in a given per-
sonal schedule S
p
. Definition 11 to 13 can (assuming
V containts n elements) be rewritten:
V = {v
p,i
|i ∈ T
N
x
}
U
α,β
= {k|v
p,k
∧ k ∈ T
N
x
∧ (α ≤ k ≤ β)}
F
α,β
= {k|¬v
p,k
∧ k ∈ T
N
x
∧ (α ≤ k ≤ β)}
A min
total = min
t
constraint can be translated to
SAT by using the general procedure from the previ-
ous section to express:
u
min
t
⇔ |U
1,n
| ≥ min
t
A max total = max
t
constraint means at least n −
max
t
variables should be assigned false. Analogously,
this can be expressed by translating
f
n−max
t
⇔ |F
1,n
| ≥ n − max
t
The translation of pertType constraints is similar.
Only difference is that the set of variables V is lim-
ited to those corresponding to a specific value j.
V = {v
p,i
|i ∈ T
N
x
∧ N
x
(i) = j}
5 APPLICATION: HARDNESS
STUDY FOR NURSE
ROSTERING PROBLEM
INSTANCES
Empirical hardness can be understood as the com-
plexity of a problem instance, when solved with a
particular solution method, measured by some per-
formance criteria. This hardness is a combination of
the intrinsic hardness of the instance and the quality
of the procedure on this specific instance. This im-
plies that empirical hardness is inherently linked to
the algorithm that is used. Empirical hardness models
typically map a set of instance features onto a perfor-
mance criterion such as the running time of an algo-
rithm.
Instance features are often derived from expert
knowledge. However, experts may be biased and
good experts in the problem domain may not always
be available. Therefore, by translating the problem in-
stances under study to SAT, we examine the feasibil-
ity of a more general approach based on well known
SAT-features (Nudelman et al., 2004).
For the hardness studies presented in this paper,
we follow the methodology presented by (Leyton-
Brown et al., 2006). Six steps are to be followed:
1. Identification of the problem instance distribution.
2. Selection of one or more algorithms and perfor-
mance criteria.
3. Selection of a set of inexpensive, distribution in-
dependent features.
4. Sampling the instance distribution for generating
a training set.
5. Elimination of redundant and uninformative fea-
tures.
6. Learning models that map the feature space onto
the performance criteria.
As hardness studies are not the scope of this paper,
we refer to the aforementioned paper for more details
on the method used and the technical report (Mes-
selis et al., 2012) for specific and detailed information
on the above steps in the light of the nurse rostering
problem. We present the results of two performed ex-
periments to demonstrate the applicability of the SAT
translation schemes presented in this paper.
The first experiment focusses on the applicabil-
ity of the SAT features proposed in (Nudelman et al.,
2004). We designed a problem instance distribution
consisting of “smaller” problem instances
2
.
The second experiment demonstrates the applica-
bility of hardness models to real world like optimi-
sation problems. Testbed were randomisations of the
instances found in the First international nurse roster-
ing competition (Haspeslagh et al., 2012).
5.1 Applicability of Hardness Studies
using SAT Features for NRP
As stated before, a problem distribution of “smaller”
instances is generated. This allows the use of IBM
CPLEX to solve the instances. Besides an optimal
2
Smaller denotes a small planning horizon, a limited
number of employees available and a limited number of
shift to be covered.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
308
Title Suppressed Due to Excessive Length 11
Fig. 1 Optimal objective value versus predicted optimal value.
NOTE: NRP model testset is a fake
NRP model - test set
0
10
20
30
40
50
60
70
0 10203040506070
real optimal value
predicted optimal value
(a) based on the NRP feature set
SAT model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real optimal value
predicted optimal value
(b) based on the SAT feature set
There appears to be some loss in accuracy when compared to the models
for the quality of the optimal solution. This can be explained by the
fact that the metaheuristic is not always able to solve an instance to
optimality. For many instances of the distribution, the metaheuristic
does find the optimal solution. For a much smaller number of instances,
the metaheuristic can only approximate the solution. This data is thus
the same data as for the complete search method, augmented with
some noise for a small set of instances. This noise produced by the
metaheuristic is hard to model. Nevertheless, these models are still very
accurate and yield good predictive power, as the plots show.
Fig. 2 Metaheuristic obtained objective value versus predicted metaheuristic value.
NRP model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real approximate quality
predicted approximate quality
(a) based on the NRP feature set
SAT model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real approximate quality
predicted approximate quality
(b) based on the SAT feature set
– Quality gap
The regression models for the quality gap are not as accurate as the
models for solution quality. The correlation coefficients are R
2
= 0.40
Figure 1: Prediction of the optimal solution quality.
Title Suppressed Due to Excessive Length 11
Fig. 1 Optimal objective value versus predicted optimal value.
NOTE: NRP model testset is a fake
NRP model - test set
0
10
20
30
40
50
60
70
0 10203040506070
real optimal value
predicted optimal value
(a) based on the NRP feature set
SAT model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real optimal value
predicted optimal value
(b) based on the SAT feature set
There appears to be some loss in accuracy when compared to the models
for the quality of the optimal solution. This can be explained by the
fact that the metaheuristic is not always able to solve an instance to
optimality. For many instances of the distribution, the metaheuristic
does find the optimal solution. For a much smaller number of instances,
the metaheuristic can only approximate the solution. This data is thus
the same data as for the complete search method, augmented with
some noise for a small set of instances. This noise produced by the
metaheuristic is hard to model. Nevertheless, these models are still very
accurate and yield good predictive power, as the plots show.
Fig. 2 Metaheuristic obtained objective value versus predicted metaheuristic value.
NRP model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real approximate quality
predicted approximate quality
(a) based on the NRP feature set
SAT model - testset
0
10
20
30
40
50
60
70
0 10203040506070
real approximate quality
predicted approximate quality
(b) based on the SAT feature set
– Quality gap
The regression models for the quality gap are not as accurate as the
models for solution quality. The correlation coefficients are R
2
= 0.40
Figure 2: Prediction of the solution quality obtained by the
metaheuristic.
solver, a variable neighbourhood metaheuristic algo-
rithm (Burke et al., 2008) is applied.
Using a selected set of features
3
, we were able
to predict the quality of the optimal solution and the
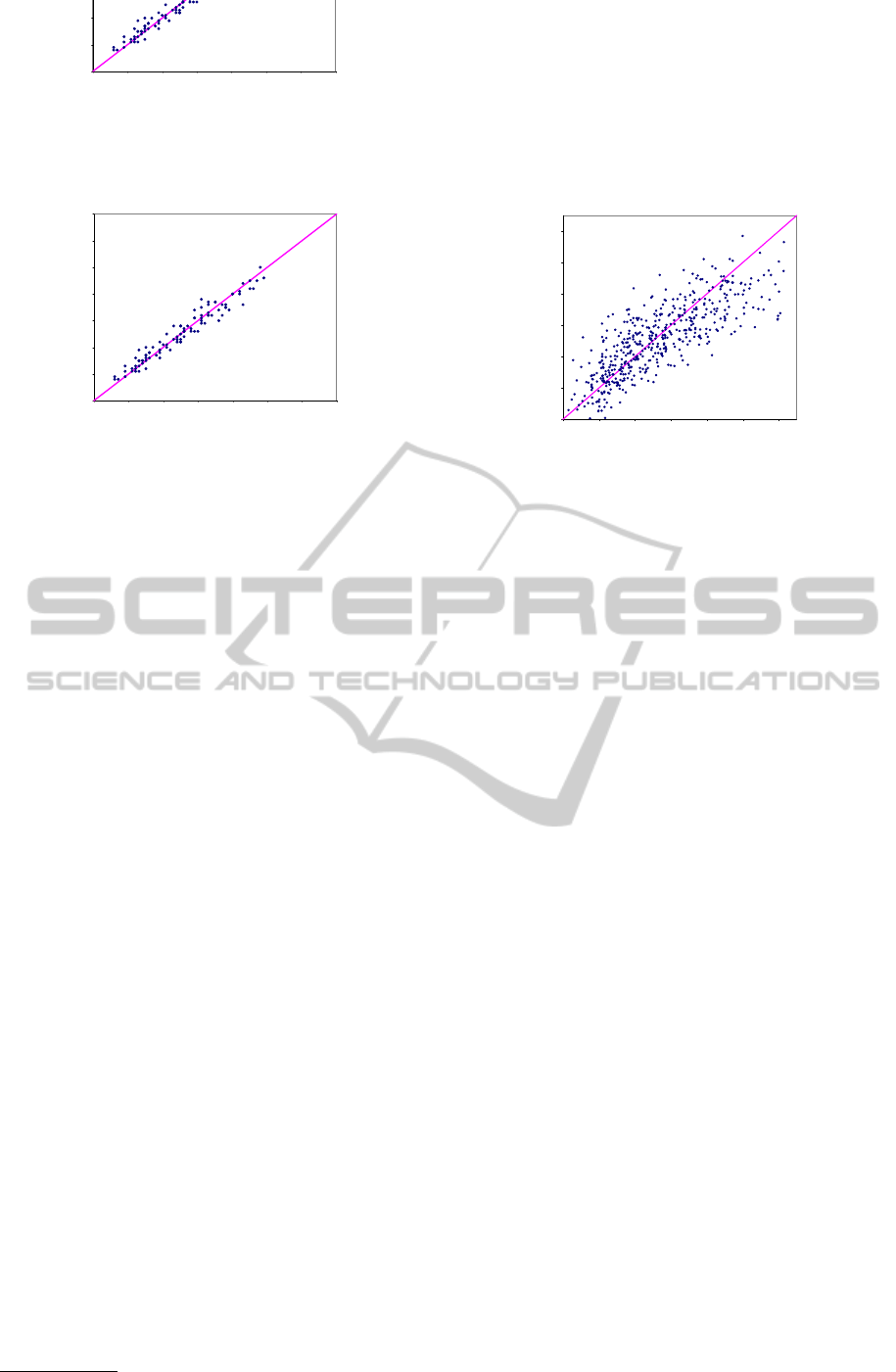
quality of the approximate solution. Figure 1 shows a
plot of the real optimal objective function values ver-
sus the predicted values on the test instances. We
found as correlation coefficient: R
2
= 0.99. Fig-
ure 2 shows a plot of the actual metaheuristic objec-
tive function values versus the predicted values. A
correlation coefficient R
2
= 0.96 is obtained.
5.2 SAT-based Hardness Analysis for
“Real World” NRP
The initial experiment served as a quick proof-of-
concept study to check the applicability of the ap-
proach to a small optimisation problem. The same
ideas were applied in the context of larger, real world
like optimisation problem instances as found in the
nurse rostering competition (Haspeslagh et al., 2012).
The feature set and the used algorithm are the same
as in the previous experiment, the performance cri-
terion under study is the quality of the approximate
solution obtained by the metaheuristic. Because of
3
Details on the features can be found in the technical
report (Messelis et al., 2012)
Title Suppressed Due to Excessive Length 15
6. Learning models that map feature space onto the performance criteria.
The models are built using statistical linear regression techniques. The
same iterative strategy as for the initial experiment is used. We compare
both resulting models.
Figure 4 shows a plot of the objective function values versus the predicted
values on the test instances, (a) for the model based on NRP features, and
(b) for the model based on SAT features. Both models are very accurate,
the NRP model has a correlation coefficient R
2
= 0.987, the model based
on SAT features achieves a very similar correlation coefficient R
2
= 0.985.
Although both models have more or less the same correlation coefficient,
the graphs show that the data points in the NRP model lie closer to the
diagonal. This can also be seen when observing the standard error of both
models. The standard error in the NRP model is 1055 while the error in
the SAT model is 1158.
Fig. 4 Metaheuristic obtained objective value versus predicted metaheuristic value.
NRP model
4000
6000
8000
10000
12000
14000
16000
4000 6000 8000 10000 12000 14000 16000
real quality
predicted quality
(a) based on the NRP feature set
SAT model
4000
6000
8000
10000
12000
14000
16000
4000 6000 8000 10000 12000 14000 16000
real quality
predicted quality
(b) based on the SAT feature set
The correlation coefficients indicate that the predictive power of the model
is high. The standard error is relatively high. This is probably due to the
fact that the metaheuristic is not particularly tuned to this experiment.
The SAT model contains structure based, balance based and Horn prox-
imity based features. As in the initial experiment, we observe a similar
importance of the node degree statistics. In addition, Horn features have
gained importance for these larger problem instances. The NRP model con-
tains features related to the weighted consecutive working and free days
in the schedule, and the number of shifts in the planning horizon. These
values are important for the prediction of the quality of the solution offered
by the metaheuristic. We showed that a feature set for hardness prediction
can be determined for the given algorithms.
Figure 3: Prediction of the solution quality obtained by the
metaheuristic.
the larger sizes of the instances, compared to the ones
of the previous experiment, the use IBM CPLEX is
no longer feasible. Figure 3 shows a plot of the ob-
jective function values obtained by the metaheuristic
versus the predicted values. A correlation coefficient
of R
2
= 0.985 is obtained. This coefficient indicates
the predictive power of the model is high.
6 CONCLUSIONS & FURTHER
RESEARCH
The main contribution of this paper is the automated
translation of nurse rostering problem instances into
SAT problems instances. To support automated trans-
lation, a formal description of nurse rostering problem
instances is required. We used numberings (Burke
et al., 2001) for clearly and unambiguously describ-
ing instances (Haspeslagh et al., 2012). We defined
eight generic constraint types allowing the representa-
tion of a large number of real world constraints found
in literature. For each constraint type, we presented
efficient translation schemes to SAT. The preprocess-
ing step for both the SAT translation introduces O(n)
variables and O(n) clauses. The SAT translation of
the consecutiveness and between constraints gener-
ates O(n) clauses. The SAT translation of count-
ing constraints generates O(n
2
) clauses and O(nlogn)
variables. Summarized, all constraints that can be
expressed as monotonic ascending numberings can
be translated to SAT. The automated translation al-
lows for an error safe representation of nurse roster-
ing problem instances as instances of other problem
domains. A manual translation can be very time con-
suming and complete equivalence between the origi-
nal and the translated model may be hard to attain.
This approach allows studying problems from an
other point of view. As shown in Section 5, the
SAT translation scheme was successfully used to
study the hardness of nurse rostering problem in-
AnEfficientTranslationSchemeforRepresentingNurseRosteringProblemsasSatisfiabilityProblems
309

stances.Although the aims of the algorithms for which
the SAT feature set (Nudelman et al., 2004) was de-
veloped is very different from the aims of algorithms
within the field of nurse rostering research (satisfia-
bility versus optimality), the relevance of SAT fea-
tures for the hardness analysis of nurse rostering prob-
lem instances was demonstrated. As we translate
to SAT, information on the objective function of the
original problem is lost. As a natural extension, the
SAT translation scheme can be adapted to produce
MAX-SAT instances thereby ’incorporating informa-
tion on the objective function’. In a first effort, MAX-
SAT solvers (Argelich and Many
`
a, 2006) can be ap-
plied to study the solution quality obtained by those
solvers. Another research direction is to design hybrid
solvers. Current efforts first try to solve a partial prob-
lem with an exact solver (Burke and Curtois, 2011;
Valouxis et al., 2012). The obtained solution is then
optimised using for example a metaheuristic. One
interesting research challenge is to study the oppo-
site. SAT solvers are able to search the entire solution
space. A metaheuristic search method only explores
the solution space partially. In a sense, metaheuris-
tics are designed for trying to escape local optima in
the solution space, e.g. a metaheuristic is used to in-
corporate diversification in the search process. By
adding extra constraints, based on the solutions ob-
tained by a metaheuristic search method, we can force
the (MAX-)SAT solvers not to explore those parts of
the solution space covered by the metaheuristic search
and therefore try to intensify diversification.
REFERENCES
Acharyya, S. (2008). A SAT Approach for Solving The
Nurse Scheduling Problem. In IEEE Region 10 Con-
ference.
Argelich, J. and Many
`
a, F. (2006). Exact max-sat solvers
for over-constrained problems. Journal of Heuristics,
12:375–392.
As
´
ın, R., Nieuwenhuis, R., Oliveras, A., and Rodr
´
ıguez-
Carbonell, E. (2009). Cardinality networks and their
applications. In Proceedings of the 12th International
Conference on Theory and Applications of Satisfiabil-
ity Testing, SAT ’09, pages 167–180.
Bailleux, O. and Boufkhad, Y. (2003). Efficient CNF En-
coding of Boolean Cardinality Constraints. In Rossi,
F., editor, Principles and Practice of Constraint Pro-
gramming - CP 2003, volume 2833 of Lecture Notes
in Computer Science, pages 108–122. Springer Berlin
/ Heidelberg.
Bilgin, B., De Causmaecker, P., Haspeslagh, S., Messelis,
T., and Vanden Berghe, G. (2009). Hardness studies
for nurse rostering problems. In LION, Trento, Italy,
14-18 January 2009.
Burke, E. and Curtois, T. (2011). New computational results
for nurse rostering benchmark instances. technical re-
port, 2011. Technical report, School of Computer Sci-
ence, University of Nottingham.
Burke, E. K., Curtois, T., Post, G., Qu, R., and Veltman,
B. (2008). A hybrid heuristic ordering and variable
neighbourhood search for the nurse rostering prob-
lem. European Journal of Operational Research,
188(2):330 – 341.
Burke, E. K., De Causmaecker, P., Petrovic, S., and
Vanden Berghe, G. (2001). Fitness Evaluation for
Nurse Scheduling Problems. In Proceedings of the
Congress on Evolutionary Computation (CEC2001),
pages 1139–1146.
Cadoli, M. and Schaerf, a. (2005). Compiling problem
specifications into SAT. Artificial Intelligence, 162(1-
2):89–120.
Cook, S. A. (1971). The complexity of theorem-proving
procedures. In Proceedings of the third annual ACM
symposium on Theory of computing, STOC ’71, pages
151–158.
C
ˆ
ot
´
e, M.-C., Gendron, B., Quimper, C.-G., and Rousseau,
L.-M. (2011). Formal languages for integer program-
ming modeling of shift scheduling problems. Con-
straints, 16(1):54–76.
Haspeslagh, S., DeCausmaecker, P., Schaerf, A., and Stle-
vik, M. (2012). The first international nurse roster-
ing competition 2010. Annals of Operations Research,
pages 1–16. 10.1007/s10479-012-1062-0.
Leyton-Brown, K., Nudelman, E., and Shoham, Y. (2006).
Learning the empirical hardness of optimization prob-
lems: The case of combinatorial auctions. In Van Hen-
tenryck, P., editor, Principles and Practice of Con-
straint Programming - CP 2002, volume 2470 of
Lecture Notes in Computer Science, pages 91–100.
Springer Berlin / Heidelberg.
Messelis, T., Haspeslagh, S., Vanden Berghe, G., and De
Causmaecker, P. (2012). Hardness studies for nurse
rostering problems using sat features. Technical re-
port, CODeS, Department of Computer Science, KU
Leuven KULAK.
Nudelman, E., Leyton-Brown, K., Hoos, H., Devkar, A.,
and Shoham, Y. (2004). Understanding random sat:
Beyond the clauses-to-variables ratio. In Wallace,
M., editor, Principles and Practice of Constraint Pro-
gramming - CP 2004, volume 3258 of Lecture Notes
in Computer Science, pages 438–452. Springer Berlin
/ Heidelberg.
Sinz, C. (2005). Towards an optimal cnf encoding
of boolean cardinality constraints. In Proceedings
of the 11th International Conference on Principles
and Practice of Constraint Programming (CP 2005),
pages 827–831.
Valouxis, C., Gogos, C., Goulas, G., Alefragis, P., and
Housos, E. (2012). A systematic two phase approach
for the nurse rostering problem. European Journal of
Operational Research, 219(2):425 – 433.
Xu, L., Hutter, F., Hoos, H. H., and Leyton-Brown, K.
(2008). Satzilla: portfolio-based algorithm selection
for sat. J. Artif. Int. Res., 32(1):565–606.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
310
