
Planning Practical Paths for Tentacle Robots
Jing Yang, Robert Codd-Downey, Patrick Dymond, Junquan Xu and Michael Jenkin
Department of Computer Science and Engineering, York University, 4700 Keele Street, Toronto, Canada
Keywords:
Path Planning, Tentacle Robotics, Redundant Manipulators.
Abstract:
Robots with many degrees of freedom with one fixed end are known as tentacle robots due to their similarity
to the tentacles found on squid and octopus. Tentacle robots offer advantages over traditional robots in many
scenarios due to their enhanced flexibility and reachability. Planning practical paths for these devices is chal-
lenging due to their high degrees of freedom (DOFs). Sampling-based path planners are a commonly used
approach for high DOF planning problems but the solutions found using such planners are often not practical
in that they do not take into account soft application-specific constraints during the planning process. This
paper describes a general sample adjustment method for tentacle robots, which adjusts the randomly gener-
ated nodes within their local neighborhood to satisfy soft constraints required by the problem. The approach
is demonstrated on a planar tentacle robot composed of ten Robotis Dynamixel AX-12 servos.
1 INTRODUCTION
Tentacle robots (see Figure 1), also knownas snake or
serpentine robots, are manipulator robots with many
degrees of freedom (DOFs). Such devices have re-
ceived considerable attention from the robotics com-
munity due to their applicability in a wide range of
different domains. Surveys on tentacle robots are pro-
vided in (Transeth et al., 2009) and (Rollinson and
Choset, 2011). Tentacle robots are often an attractive
alternative to traditional robotic systems for difficult
terrains and challenging grasping scenarios. These
applications include search and rescue missions in
complex urban environments, planetary surface ex-
ploration, minimally invasive surgery, and inspection
of piping and nuclear systems (Choset and Henning,
1999; Gayle et al., 2007; Buckinham and Graham,
2011). Unlike traditional manipulator robots which
tend to have small numbers of DOFs, tentacle robots
utilize redundantDOF’s in order to enhance their abil-
ity to deal with complex environments and tasks.
Path planning is a fundamental problem for nearly
all the robotic systems. The basic robot path plan-
ning problem involves finding a path for a robot to
get from ‘here’ to ‘there’ while avoiding any obsta-
cles in a static environment. It has been proven that
the basic path planning problem is PSPACE-complete
in the dimensionality of the DOFs possessed by the
robot (Reif, 1979; Canny, 1988). As a consequence,
a number of probabilistic sampling-based planners
have been developed to solve high-dimensional real-
world path planning problems (a summary is provided
in (Tsianos et al., 2007)) such as the planning problem
encountered with tentacle robots.
Since it can be hard to plan a path for robots with
many DOFs, most methods for high DOF robots aim
at finding any solution within a reasonable time. With
the development of sampling-based algorithms and
their application in practice, the focus has shifted to
considering the quality of the path obtained (Raveh
et al., 2011; Geraerts, 2006; Kim et al., 2003; Garber
and Lin, 2002; Wein et al., 2005; Bayazit, 2003; Song
et al., 2001; Karaman and Frazzoli, 2011). A short-
coming of basic sampling-based planning approaches
is that they often obtain highly ‘non-optimal’ solu-
tions since they rely upon randomization to map or
explore the search space. Although these algorithms
may find a valid solution, that solution may not be
practical in that it does not meet soft constraints that
exist within the problem domain. Furthermore, it
has been proven that standard PRM and RRT are not
asymptotically optimal, i.e. the cost of the solution
returned by the algorithm will not converge to the op-
timal cost as the number of samples increases (Kara-
man and Frazzoli, 2011).
The need to properly represent and use soft con-
straints is particularly important for redundant DOF
robots such as tentacle devices. For these devices
the high number of DOFs provide the opportunity to
deal with complex environments and to produce so-
lutions that are not only correct (e.g., they grasp the
object through free space, for grasping tasks) but that
128
Yang J., Codd-Downey R., Dymond P., Xu J. and Jenkin M..
Planning Practical Paths for Tentacle Robots.
DOI: 10.5220/0004263501280137
In Proceedings of the 5th International Conference on Agents and Artificial Intelligence (ICAART-2013), pages 128-137
ISBN: 978-989-8565-38-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Figure 1: A planar tentacle robot with ten links.
they also optimize other requirements of the problem
space. One common way of taking these constraints
into account is to use an appropriate controller that
takes the path identified by the path planner as input
and then integrates the soft constraints while follow-
ing the path (Bruce and Veloso, 2005; Kobilarov and
Sukhatme, 2005). There are many issues with this
approach. Perhaps most critically the paths produced
may be infeasible for a real robot. For example, fol-
lowing the path produced may require that the robot
move extremely slowly in order to minimize the in-
fluence of dynamics and other physical constraints.
These controllers are also system specific, and it can
be very hard to develop a good ‘general’ controllers
or to know which controller to use for which task.
A more general approach is to augment sampling-
based path planning with mechanisms to provide
paths that are both correct but that also optimize soft
constraints. Such augmentation could take place at
different points in the path planning algorithm. Here
we concentrate on optimizations performed during
the sampling phase of the algorithm. Specifically we
perturb each randomly generated sample within its
local neighborhood in order to enhance compliance
with the soft constraints. We show that this often
leads to more practical paths for the robot. The frame-
work described here is intended to be robot indepen-
dent, but the approach is described and tuned here to-
wards capabilities and tasks associated with the planar
tentacle robot shown in Figure 1.
This paper is structured as follows: Section 2 re-
views existing sampling-based planning algorithms
that address the path quality problem and the current
methods used to plan paths for tentacle robots. Sec-
tion 3 formulates the practicality of paths in terms
of soft constraints and describes constraints particu-
larly critical for tentacle robots. In Sections 4 and 5,
path planning strategies are developed to find paths of
user-preferred qualities based on this formalism. Sec-
tion 6 includes comparison results from applying the
practicality-based approach and basic PRM to differ-
ent test environments using both real and simulated
tentacle robots. Finally Section 7 summarizes the
work and provides possible directions for future re-
search.
2 RELATED WORK
2.1 Sampling-based Path Planning
Instead of computing an exact representation of the
planning space, sampling-based planners generate
samples and test motions in configuration space. Such
planners usually represent motions as a graph as in
the Probabilistic Roadmap Method (PRM) (Kavraki
et al., 1996; Kavraki et al., 1998), or as a tree as in the
Rapidly-exploring Random Tree (RRT) (LaValle and
Kuffner, 2000). These methods are probabilistically
complete and it is not guaranteed that these planners
will find a path even though one exists, but if they do
find a path the path will take the device from the initial
configurationto the goal. With the developmentof the
sampling-based algorithms and their application in
practice, focus in the research community has shifted
to considering the quality or practicality of the com-
puted path. Randomized path planning algorithms ad-
dressing the path quality problem can be divided into
three broad categories based on where practical issues
are integrated within the algorithm: pre-processing,
post-processing, and customized learning.
Pre-processing Approaches. Pre-processing ap-
proaches consider the specific preferences of de-
sired paths in the pre-processing phase, i.e. during
the roadmap construction phase before a query is
made. Because of its probabilistic nature, the PRM
roadmap often contains nodes and edges that lack
practical usage or are redundant. Aiming at find-
PlanningPracticalPathsforTentacleRobots
129

ing shorter paths with higher clearance, Nieuwen-
huisen and Overmars (Nieuwenhuisen and Overmars,
2004) proposed to add nodes and edges to create “use-
ful” cycles, which provide short paths and alternative
paths in different homotopy classes. Based on this
work, a PRM variant also attempts to retract nodes
and edges to the medial axis for generating high clear-
ance paths (Geraerts, 2006).
Post-processing Approaches. Given a path found
by the sampling-based path planner, post-processing
approaches modify the path in accordance with the re-
quired practicality preference by adding new nodes,
smoothing it, eliminating unnecessary loops or de-
tours, etc. Path pruning and shortcut heuristics
are common post-processing techniques for creat-
ing shorter and smoother paths (Hsu, 2000; Ger-
aerts, 2006). Two retraction algorithms are presented
to add clearance to a given path, one based in the
workspace and the other one based in the configu-
ration space (Geraerts and Overmars, 2005). Post-
processing algorithms may take multiple paths as in-
puts rather than just a single one. For example, the
path merging algorithm described in (Raveh et al.,
2011) computes a path with improved quality by hy-
bridizing high-quality sub-paths from the initial input
paths. The algorithm considers the generalized for-
mulation of path quality measures rather than specific
requirements.
Customized Learning. Although post-processing
algorithmshave shownsome success in improving the
path quality and can be used by all the path planners,
the final path depends on the original paths, i.e. they
cannot find alternative routes that deviate consider-
ably from the original ones. To avoid this problem,
customized learning algorithms integrate the require-
ment for path quality in the learning phase. For exam-
ple, Kim et al. (Kim et al., 2003) use an augmented
version of Dijkstra’s algorithm to extract a path from
a roadmap on criteria other than path length.
The approach of initially finding an approxi-
mate solution is utilized by the Fuzzy PRM (Nielsen
and Kavraki, 2000), Lazy PRM (Bohlin and
Kavraki, 2000), IRC (Iterative Relaxation of Con-
straints) (Bayazit, 2003) and C-PRM (Customizable
PRM) (Song et al., 2001) algorithms where the
roadmap nodes and edges are not validated, or are
only partially validated, during roadmap construc-
tion. During the learning phase, the path is searched
by strengthening the constraints (obstacle collision,
path length or other specified preferences) iteratively.
These methods are designed to decrease the roadmap
construction costs, while only increasing the query
costs slightly.
2.2 Path Planning for Tentacle Robots
There has been relatively little work devoted ex-
plicitly to tentacle robot path planning. One ap-
proach is based on the definition of tunnels in the
workspace (Chirikjian and Burdick, 1990). Meth-
ods from differential geometry are then used to guar-
antee that the tentacle is confined to the tunnels,
and therefore avoids any obstacles. This work does
not prescribe any strategy for constructing the tun-
nels. Later, it was proposed to use the results of the
Generalized Voronoi Graph (GVG) approach to con-
struct the tunnels. Motion planning is then achieved
via a nose-following approach which allows the end-
effector to move along the GVG followed by the rest
of body (Choset and Henning, 1999).
Sampling-based planning algorithms such as
PRMs and RRTs are popular because of their suc-
cess in a wide range of applications and in high-
dimensional configuration spaces. This makes them
an appealing choice for tentacle robot path planning,
but they still suffer from the problem of generating
less than optimal paths of the robot. Aiming at finding
realistic paths for highly articulated chain a physics-
based sampling strategy is presented in (Gayle et al.,
2007). The method exploits the coherence between
joint angles via the “adaptive forward dynamics”
framework in order to determine which joints have
the greatest impact on the overall motion. Then, only
the most important joints are simulated. The samples
are then biased by using constraint forces designed to
avoid collisions while moving toward the goal (simi-
lar to the potential field approach). Simulations show
that the planner was able to find more natural paths
than the PRMs and RRTs that used straight-line local
planners.
3 PROBLEM STATEMENT
In basic path planning (Latombe, 1991), given a robot
A , a static workspace W containing a set of obstacles,
an initial configuration θ
init
and a goal configuration
θ
goal
, the objective of path planning is to determine a
feasible path P between θ
init
and θ
goal
. The definition
of feasible paths only considers geometric constraints
that arise from collision with obstacles and is often in-
adequate to describe realistic path planning problems.
Soft constraints can be added to the basic path
planning problem in a number of different ways. Fol-
lowing the PDDL3.0 approach (Gerevini and Long,
2005), the syntax for soft constraints can be bro-
ken down into two components: (i) the identifica-
tion of the soft constraints; and (ii) the description
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
130

of how the satisfaction or lack of these constraints
affects the quality of the result. Similar to the de-
scriptions of hard constraints, soft constraints are also
described using predicates of the planning problem.
Each binary soft constraint is associated with a vio-
lation penalty weight such that paths, or portions of
paths that satisfy different subsets of soft constraints
can be compared. Let S be the set of soft constraints.
The following are typical soft constraints for tentacle
robots described in terms of inequalities between the
value computed from the robot’s configuration and a
corresponding threshold λ:
Safe Clearance from Obstacles (SCO). A soft
constraint for keeping a safe clearance from the ob-
stacles (Zghal and Dubey, 1990) is given by
N
∑
i=1
1
D
i
!
≤ λ
SCO
(1)
where D
i
is the distance between the i-th link of
the manipulator and obstacles, and λ
SCO
is the pre-
defined upper bound (similar to λ
JLA
and λ
PEE
be-
low);
Joint Limit Avoidance (JLA). A soft constraint
for joint limit avoidance (Zghal and Dubey, 1990) is
given by
N
∑
i=1
θ
i,Max
− θ
i,Min
(θ
i,Max
− θ
i
)(θ
i
− θ
i,Min
)
!
≤ λ
JLA
(2)
where θ
i,Max
and θ
i,Min
are the maximum and min-
imum permissible joint angles and θ
i
is the current
joint angle for the i-the joint.
Precision of End-Effector (PEE). It is often re-
quired to ensure the precision with which a tentacle
robot approaches a point or follows a path defined
by the pose of the end-effector (EEF) (Hill and Tesar,
1997). Let x ∈ R
m
represent the output position vec-
tor of the EEF and θ ∈ R
n
the vector of joint angles of
the robot. An infinitesimal error in the EEF position
can be mapped from the joint errors through:
∆x = J∆c (3)
where the m× n matrix J, called the Jacobian, is a ge-
ometrically dependent structure relating the joint er-
rors to the output errors (Manseur, 2006; Khalil and
Dombre, 2002). The Euclidean norm of the EEF error
is therefore bounded above by
k∆xk
k∆ck
≤ σ
max
(4)
where σ
max
is the Jacobian’s maximum singular val-
ues. A soft constraint for the generalized EEF preci-
sion can be defined by bounding σ
max
:
σ
max
≤ λ
PEE
(5)
Note that we do not attempt to distinguish degrees of
satisfaction of a soft constraint – we are only con-
cerned with whether or not the constraint is satisfied.
However, a soft constraint may be counted multiple
times depending on the number of the violation oc-
currences exhibited while executing the path. Let P
denote the set of all feasible paths. Here we define
the cost function that describes the overall practical-
ity of a path and then define the path planning with
soft constraints using the cost function.
Cost Function. Consider a feasible configuration
θ ∈ C
free
, where C
free
is the free configuration space,
i.e θ meets all the hard constraints, e.g., not colliding
with the surrounding obstacles and staying within the
joint limits. Given a soft constraint s, the cost func-
tion of the configuration cost
s
: C
free
→ [0, 1], i.e. a
cost
s
(θ) ∈ [0, 1] can be computed for each θ ∈ C
free
.
This cost function can be continuous or discrete. In
its simplest version, the cost function cost
s
is binary,
which is 0 when the soft constraint is satisfied by θ,
and 1 when violated.
Furthermore, given a set of soft constraints S with
associated violation penalty weights, the cost of the
feasible configuration is the summation of the penalty
weights of all the cost of soft constraints that are vio-
lated by θ, defined as
cost : C
free
→ R
≥0
, cost(θ) =
∑
s∈S
w(s)·cost
s
(θ) (6)
where w(s) is a positive value that represents the vi-
olation penalty weight associated with the soft con-
straint s. A path P of length l is represented by a
unit-speed parametric function τ : [0, l] → C
free
with
τ(t) = θ
t
∈ P . Then the parametric cost function can
be defined:
v : [0, l] → R
≥0
v(t) = cost ◦ τ(t) = cost(θ
t
) (7)
Given a feasible path P , its cost is the integral of the
cost of all the configurations along the path, defined
as
cost : P → R
≥0
, cost(P ) =
Z
l
0
v(t)dt (8)
A discrete approximation of the integral leads to
cost : P → R
≥0
, cost(P ) ∼
1
n
n−1
∑
k=0
v((
k
n− 1
)l) (9)
Which provides a cost function that penalizes paths
with sections that violate the soft constraints pro-
vided.
PlanningPracticalPathsforTentacleRobots
131

Algorithm 1: Roadmap Generation with Soft Constraints.
1: V ←
/
0
2: E ←
/
0
3: for i = 1, ..., n do
4: θ
rand
← sampling with soft constraints
5: V ← V ∪ {θ
rand
}
6: end for
7: for all v ∈ V do
8: X ← Near(G = (V, E), θ
rand
, r)
9: for all x ∈ X do
10: if (v, x) H then
11: E ← E ∪ {(v, x), (x, v)}
12: end if
13: end for
14: end for
15: return G = (V,E)
Path Planning with Soft Constraints. Given a
path planning problem (A , W , θ
init
, θ
goal
), a set of
soft constraints S with corresponding penalty weights
and a cost function cost, generate a feasible path P
such that cost(P ) is minimized. Report failure if no
feasible path can be found.
4 SAMPLING WITH SOFT
CONSTRAINTS
PRM was designed to answer multiple path queries
for a high-DOF robot in cluttered environments. In
order for the algorithm to find not only correct paths
but also paths that minimize violations of soft con-
straints the basic method must be refined. Here we
describe the integration of the node-based soft con-
straints in the sampling phase of the PRM.
Following (Kavraki et al., 1998), the PRM
roadmap generation is outlined in Algorithm 1.
During node generation, instead of choosing com-
pletely random configurations, our sampling method
with soft constraints (i.e. SamplingSC and Sam-
plingHCSC) is called (line 4) and the new configu-
ration that satisfies some or all the soft constraints is
added to the set of vertices V. Connections are then
attempted between vertices within a distance r using
a simple straight-line local planner.
It is observed that for a collision-free node to be
useful for path planning it must be part of a connected
free region. Within any region we can expect some
locations to be more practical than others. Ensuring
that more practical nodes are chosen during the seed-
ing process while still sampling the space sufficiently
densely to construct paths is likely to improve overall
path practicality, at least as measured by the node-
based soft constraints.
Given that a node was found to be feasible we can
search within a local region of this node to enhance
the practicality of this node. In order to take advan-
tage of this, the planner adjusts a node within its free
space to states with fewer soft constraint violations
before adding them to the roadmap. For efficiency
reasons, and for generality of the approach, we fol-
low the philosophy of randomness of the PRMs to
make the adjustment. We present two node adjust-
ment strategies SamplingSC and SamplingHCSC as
outlined in Algorithm 2 and 3.
Algorithm 2 : SamplingSC (random sampling with soft
constraints).
1: repeat
2: θ
rand
← a randomly chosen configuration in C
3: until θ
rand
H
4: θ
new
← θ
rand
5: for i ← 1, ..., k do
6: d ← N (0, r
∗
)
7: θ
i
← a random configuration at distance d from θ
rand
8: if θ
i
H and cost(θ
i
) < cost(θ
new
) then
9: θ
new
← θ
i
10: end if
11: end for
12: return θ
new
Algorithm 3: SamplingHCSC (random sampling with hill-
climbing soft constraint satisfaction).
1: repeat
2: θ
rand
← a randomly chosen configuration in C
3: until θ
rand
H
4: θ
new
← θ
rand
5: u ← a random direction
6: for i ← 1, ..., k do
7: θ
i
← move θ
new
in the direction of u by step size
d
step
8: if θ
i
H and cost(θ
i
) < cost(θ
new
) then
9: θ
new
← θ
i
10: else
11: return θ
new
12: end if
13: end for
14: return θ
new
In SamplingSC, for each randomly generated node
θ
new
that satisfies all the hard constraints, a user spec-
ifies the number k of attempts to adjust θ
new
to re-
duce the soft cost. New samples are generated in
θ
new
’s neighborhood according to the normal distri-
bution N (0, r
∗
), where the scale r
∗
(similar with the
radius r used to in Algorithm 1) is chosen based on the
assumed local complexity of the configuration space.
Each of these new samples is first tested for compli-
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
132

ance with the hard constraints (collision free in most
cases). If the test passes then the soft constraints are
applied. The valid node with minimum cost (i.e. it
satisfies soft constraints the most) from this sample is
then added in the roadmap.
Note that during the node adjustment step k nodes
are not added to the roadmap. Rather, each node is
augmented up to k times while retaining fixed the to-
tal number of nodes. Choosing k is an application-
specific issue. On the one hand, k should not be too
small, because we want to give our planner a good
chance to make an improvement. On the other hand,
making k too large increases the running time unnec-
essarily. In essence we assume that within some ra-
dius (defined by r
∗
) of a node, there exists a com-
mon homotopic path. In this work we assume a sin-
gle r
∗
but clearly it would be possible to set r
∗
= f(θ)
for complex non-homogeneousenvironments or to set
r
∗
= g(n) according to the density of the sampling.
SamplingHCSC is a greedy strategy that can be
considered as an alternative to SamplingSC. Instead
of attempting to reduce the cost of a sample once, the
SamplingHCSC iterates the maximum of k steps to-
ward a random direction u until a hard constraint is
violated or the cost stops decreasing. The random di-
rection u incorporates all of the degrees of freedom of
the robot.
Once the roadmap R is constructed, finding a
path between θ
init
and θ
goal
involves connecting these
points to R . If they do not belong to the same con-
nected component, then more nodes need to be gen-
erated for R to connect the components to which θ
init
and θ
goal
belong. If this cannot be accomplished after
a maximal number of trials then failure is reported.
Otherwise, it proceeds to the next phase: extracting
an optimal path from R . Given the nature of the cost
function of paths, it is possible to use Dijkstra’s al-
gorithm (Kim et al., 2003) to find the minimum cost
path in R from θ
init
to θ
goal
.
5 POSTPROCESSING WITH
SOFT CONSTRAINTS
Path smoothing is a commonly used post-processing
method that improves a found path. Path pruning and
shortcut heuristics are common path smoothing tech-
niques for creating shorter and smoother paths. The
shortcut method tries to iteratively improve the path
by replacing a part of the path with a shorter local
path. In each iteration, the path is randomly split in
three parts. Let a and b denote the begin and end
configurations of the middle part. If the local path
LP(a, b) is collision-free, then the local path replaces
the middle part. Due to their simplicity, shortcut algo-
rithms have been widely used to improve the quality
of paths computed by randomized planners (Geraerts
and Overmars, 2007).
The goal of traditional shortcutting method is to
find a shorter path that is in the same homotopy class
of an existing path. However, this can bring the robot
close to an obstacle or violate other soft constraints.
We augment the shortcut algorithm with soft con-
straints (shown in Algorithm 4) which compares the
cost of the new local path and the original part of the
path before replacement. We expect that this method
will be slower than the original heuristic as the cost
comparison takes extra computing time. However, we
expect that the resultant path will be more practical.
Algorithm 4: Shortcut with Soft Constraints (discrete path
P = θ
0
, θ
1
, ...θ
m−1
).
1: loop
2: a, b ← two random indices in [0, m) and (a < b)
3: P
1
← θ
0
, ...θ
a−1
4: P
2
← θ
a
, ...θ
b
5: P
3
← θ
b+1
, ...θ
m−1
6: if LP(θ
a
, θ
b
) H and cost(LP(θ
a
, θ
b
)) < cost(P
2
)
then
7: P ← P
1
∪ LP(θ
a
, θ
b
) ∪ P
3
8: end if
9: end loop
6 EXPERIMENTAL VALIDATION
This section describes experiments of the algorithm
using a real tentacle robot and its simulation. The
planar tentacle robot is composed of ten Robotis Dy-
namixel AX-12 servos (Figure 1). The robot is ap-
proximately 67cm long when it lies straight. One end
of the robot is fixed and rollers have been installed to
reduce friction between the robot and the table top.
The algorithms were implemented within Lavalle’s
Motion Strategy Library (LaValle, 2006), and run on
a Mac running OS X with 3.06 GHz Intel Core 2 Duo
processor and 2 GB memory.
Only one single soft constraint (SCO, JLA, and
PEE as discussed in Section 3) is considered in each
experiment. The penalty weight for each soft con-
straint is set to 1. The thresholds are set as follows:
λ
sco
= 15, λ
jla
= 50, λ
pee
= 1000.
Comparisons between the basic path planning and
path planning with soft constraints minimizing a cost
function are illustrated in Figure 2. The scene shows
a simulation of the tentacle robot operating in a
workspace comprising two obstacles. The path plan-
ners attempt to compute possible paths that takes the
PlanningPracticalPathsforTentacleRobots
133
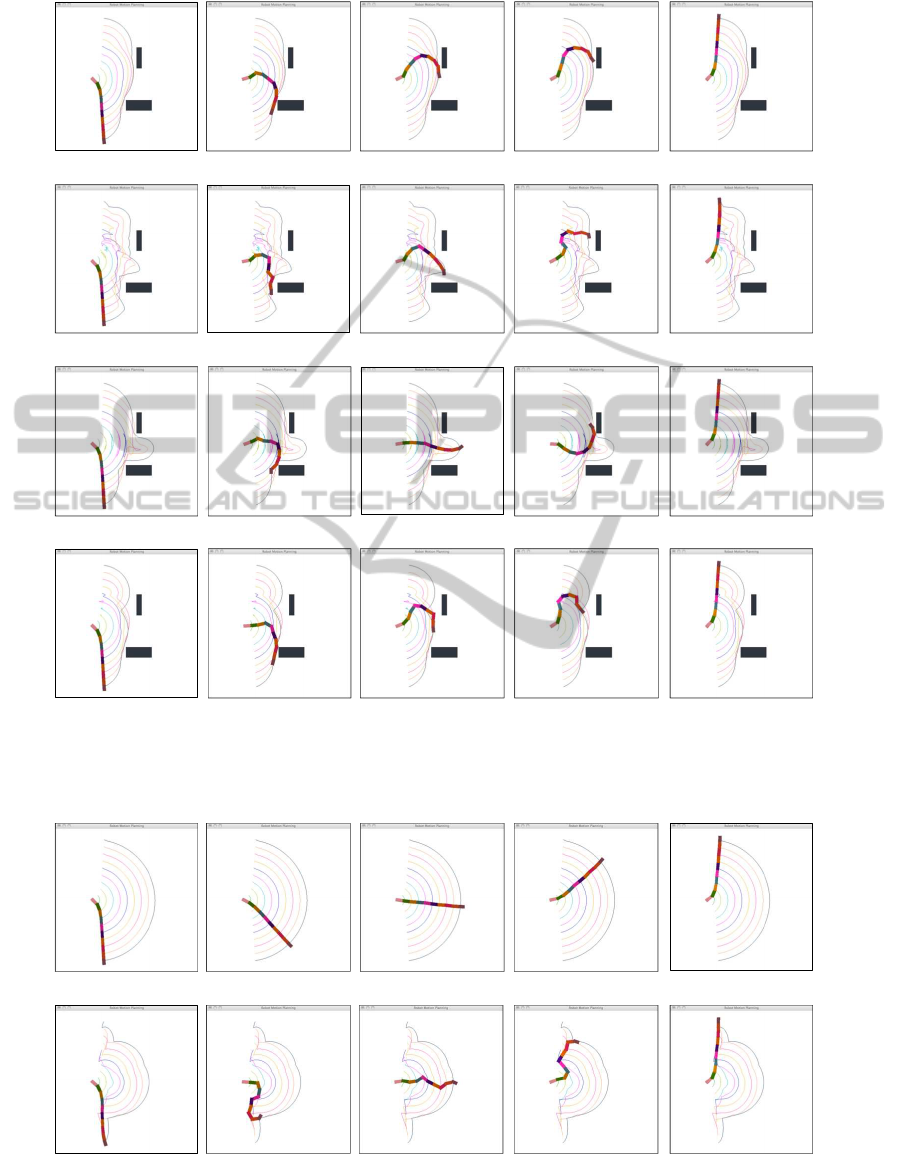
(a)
(b)
(c)
(d)
Figure 2: Path planning in a workspace with two rectangular obstacles. Comparison between (a) basic path planning; (b) path
planning with soft constraints keeping safe clearance from obstacles (SCO); (c) path planning with soft constraints avoiding
joint limits (JLA); (d) path planning with soft constraints maximizing precision of the end-effector (PEE).
(a)
(b)
Figure 3: Path planning in the absence of obstacles. Comparison between (a) basic path planning and (b) Path planning with
soft constraints maximizing the precision of end-effector (PEE).
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
134
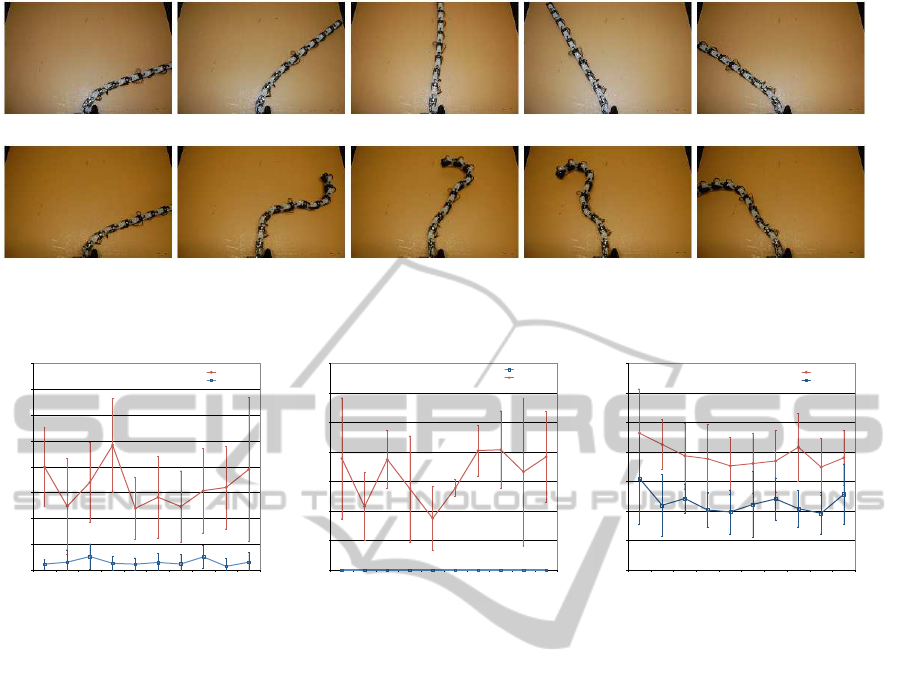
(a)
(b)
Figure 4: Snapshots of the tentacle robot executing the paths computed by: (a) basic path planning and (b) Path planning with
soft constraints maximizing the precision of end-effector (PEE).
0
20
40
60
80
100
120
140
160
3000
4000
5000
6000
7000
8000
9000
10000
11000
12000
Cost of the path
Initial Number of Seed Points
PRM
SamplingSC-SCO
0
20
40
60
80
100
120
140
3000
4000
5000
6000
7000
8000
9000
10000
11000
12000
Cost of the path
Initial Number of Seed Points
SamplingSC-JLA
PRM
10
30
50
70
90
110
130
150
3000
4000
5000
6000
7000
8000
9000
10000
11000
12000
Cost of the path
Initial Number of Seed Points
PRM
SamplingSC-PEE
(a) (b) (c)
Figure 5: Cost comparison of the paths found by PRM and SamplingSC, when the soft constraints are: (a) SCO; (b) JLA;
(c) PEE. Cost of the path is measured as the summation of the binary cost of the configurations along the discretized path.
Results are averaged for 20 independent runs for each case. Standard deviations are shown.
robot from the lower space to the upper one while
avoiding obstacles. Figure 2(a) shows a path com-
puted by the traditional PRM followed by the tradi-
tional shortcut method. The path is correct and is
relatively short. Figure 2(b) shows a path computed
by our path planner minimizing SCO, which encour-
ages to keep the robot a minimum distance away from
the obstacles. Figure 2(c) shows a path minimizing
JLA, which tries to minimize the deviation between
each joint. Therefore the robot becomes straight when
passing the gap between the two obstacles.
In practice the precision of tentacle robots is a crit-
ical issue for it to accomplish tasks and the precision
issue becomes more critical when the robot has more
joints. Here we use PEE as the soft constraint in path
planning and try to find paths that the robot can fol-
low more precisely. As discussed in Section 3 we
can increase the precision of the end-effector by re-
ducing the maximum singular value σ
max
of the Jaco-
bian matrix. It has been observed that σ
max
is max-
imized when the robot is straight, and it decreases
when the robot bends. A result path is shown in Fig-
ure 2(c). The difference is more obvious in the case
shown in Figure 3 where there is no obstacle in the
scene. Most path planners will compute a path shown
in Figure 3(a) that directly takes the path from the start
to the goal while the robot stays straight all the way.
However, maximizing the PEE gives a more complex
solution as shown in Figure 3(b). The effectiveness
of the method was further validated on the real ten-
tacle robot, to which we passed different computed
paths and it shows that our method outperforms ba-
sic PRM in terms of precision of the robot in practice.
See Figure 4 for snapshots from the executionof these
experiments.
To test our algorithm’s performance on differ-
ent soft constraints, we compare the practical path
alghorithm with the basic PRM using the problem
shown in Figure 2. We compare the SamplingSC al-
gorithm with a single soft constraint applied against
the basic PRM. Each algorithm was tested with vari-
ous numbers of seed points as described in Figure 5.
By sampling with soft constraints the average cost of
the path is decreased significantly when compared to
the basic PRM in all the three cases. The SamplingSC
method also shows more stability (smaller standard
PlanningPracticalPathsforTentacleRobots
135
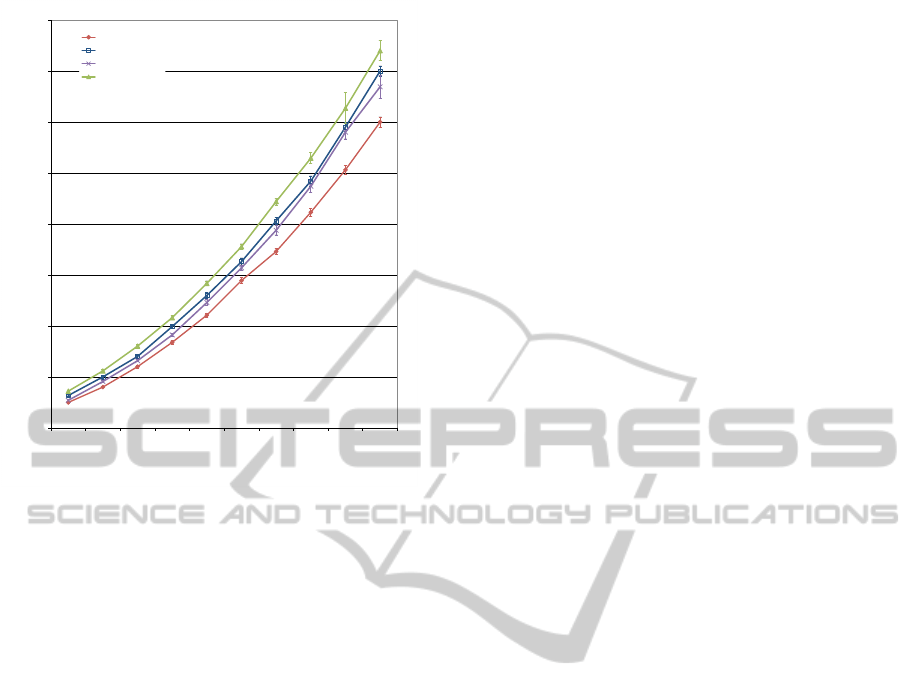
0
10
20
30
40
50
60
70
80
3000
4000
5000
6000
7000
8000
9000
10000
11000
12000
Running time (s)
Initial Number of Seed Points
PRM
SamplingSC-SCO
SamplingSC-JLA
SamplingSC-PEE
Figure 6: Comparison of the running time of the basic PRM
and SamplingSC with soft constraints being SCO, JLA and
PEE. Results are averaged for 20 independent runs for each
case. Standard deviations are shown.
deviations) than the basic PRM in the path quality
they achieve. Figure 6 compares the running time of
constructing the basic PRM and the roadmap with dif-
ferent soft constraints for the test model. It shows that
the roadmap generation with soft constraints takes
more time to compute than the PRM algorithm since
the node adjustment involves an increased number of
collision checks and computation to check the soft
constraints.
7 SUMMARY AND FUTURE
WORK
Path planning is an important but intractable prob-
lem in Robotics. Sampling-based path planning al-
gorithms are successful in solving high-dimensional
problems. However, their ability to find paths that
meet certain soft constraints is still limited. In many
applications, it is also required to find a path that is
safer or more precise than other alternative paths.
This paper describes an approach to the problem
of planning practical paths for tentacle robots in terms
of soft constraints and develops sample adjustment
strategies for sampling-based path planners to take
into account these soft constraints. The planner ad-
justs each randomly generated node in a random di-
rection within its local neighborhood to increase its
practicality (i.e. reduce its cost). Then the new node
with competitive practicality replaces the initial node
in the roadmap.
We have shown the effectiveness of our approach
using both a simulated and real tentacle robot. Three
soft constraints are used separately in the test model.
Although the resultant path is not optimal due to the
randomness of the planner, it shows significant im-
provement over the path computed by the basic PRM.
Currently we only considered node-level soft con-
straints to express the practicality of each node, i.e.
a configuration of the robot. For many problems the
transition of the adjacent configurations should also
meet certain requirements, such as the smoothness of
the transition and the acceleration of the movement.
Ongoing work includes developing path planners to
address such edge-level practicality issues.
REFERENCES
Bayazit, O. B. (2003). Solving Motion Planning Problems
by Iterative Relaxation of Constraints. PhD thesis,
Texas A&M University.
Bohlin, R. and Kavraki, L. E. (2000). Path planning using
Lazy PRM. In Proceedings IEEE International Con-
ference on Robotics & Automation (ICRA), volume 1,
pages 521–528, San Fransisco, CA, USA. IEEE Press,
IEEE Press.
Bruce, J. and Veloso, M. (2005). Real-Time Multi-Robot
Motion Planning with Safe Dynamics. In Multi-Robot
Systems: From Swarms to Intelligent Automata, vol-
ume 3.
Buckinham, R. and Graham, A. (2011). Safire - a robotic
inspection system for candu feeders. In Proceedings
International Conference on CANDU Maintenance.
Canny, J. F. (1988). The Complexity of Robot Motion Plan-
ning. MIT Press, Cambridge, MA, USA.
Chirikjian, G. S. and Burdick, J. W. (1990). An obstacle
avoidance algorithm for hyper-redundant manipula-
tors. In Proceedings IEEE International Conference
on Robotics & Automation (ICRA), volume 1, pages
625–631.
Choset, H. and Henning, W. (1999). A follow-the-leader
approach to serpentine robot motion planning. ASCE
Journal of Aerospace Engineering.
Garber, M. and Lin, M. C. (2002). Constraint-based motion
planning using Voronoi diagrams. In Proceedings In-
ternational Workshop on Algorithmic Foundations of
Robotics (WAFR).
Gayle, R., Redon, S., Sud, A., Lin, M., and Manocha, D.
(2007). Efficient motion planning of highly articu-
lated chains using physics-based sampling. In Pro-
ceedings IEEE International Conference on Robotics
& Automation (ICRA), pages 3319–3326.
Geraerts, R. (2006). Sampling-based Motion Planning:
Analysis and Path Quality. PhD thesis, Utrecht Uni-
versity.
ICAART2013-InternationalConferenceonAgentsandArtificialIntelligence
136

Geraerts, R. and Overmars, M. (2005). On improving the
clearance for robots in high-dimensional configura-
tion spaces. In Proceedings IEEE/RSJ International
Conference on Intelligent Robots and Systems (IROS),
pages 679–684.
Geraerts, R. and Overmars, M. H. (2007). Creating high-
quality paths for motion planning. International Jour-
nal of Robotics Research, 26(8):845–863.
Gerevini, A. and Long, D. (2005). Plan constraints and
preferences in pddl3 - the language of the fifth inter-
national planning competition. Technical report, Uni-
versity of Brescia.
Hill, B. and Tesar, D. (1997). Design of Mechanical Prop-
erties for Serial Manipulators. PhD thesis, University
of Texas at Austin.
Hsu, D. (2000). Randomized Single-query Motion Planning
in Expansive Spaces. PhD thesis, Stanford University.
Karaman, S. and Frazzoli, E. (2011). Sampling-based al-
gorithms for optimal motion planning. International
Journal of Robotics Research, 30(7):846–894.
Kavraki, L. E., Latombe, J.-C., Motwani, R., and Raghavan,
P. (1998). Randomized query processing in robot path
planning. Journal of Computer and System Sciences,
57(1):50–60.
Kavraki, L. E., Svestka, P., Latombe, J.-C., and Overmars,
M. (1996). Probabilistic roadmaps for path plan-
ning in high dimensional configuration spaces. IEEE
Transactions on Robotics and Automation, 12(4):566–
580.
Khalil, W. and Dombre, E. (2002). Modeling, Identification
and Control of Robots. Hermes Penton Ltd.
Kim, J., Pearce, R. A., and Amato, N. M. (2003). Ex-
tracting optimal paths from roadmaps for motion plan-
ning. In Proceedings IEEE International Conference
on Robotics & Automation (ICRA), volume 2, pages
2424–2429.
Kobilarov, M. and Sukhatme, G. S. (2005). Near time-
optimal constrained trajectory planning on outdoor
terrain. In Proceedings IEEE International Confer-
ence on Robotics & Automation (ICRA), pages 1833–
1840.
Latombe, J.-C. (1991). Robot Motion Planning. Kluwer.
LaValle, S. M. (2006). Planning Algorithms. Cam-
bridge University Press, Cambridge, U.K. Available
at http://planning.cs.uiuc.edu.
LaValle, S. M. and Kuffner, J. J. (2000). Rapidly-exploring
random trees: Progress and prospects. In Proceedings
International Workshop on Algorithmic Foundations
of Robotics (WAFR).
Manseur, R. (2006). Robot Modeling and Kinematics. Da
Vinci Engineering Press.
Nielsen, C. and Kavraki, L. E. (2000). A two-level
fuzzy prm for manipulation planning. In Proceed-
ings IEEE/RSJ International Conference on Intelli-
gent Robots and Systems (IROS), volume 3, pages
1716–1722. IEEE Press, IEEE Press.
Nieuwenhuisen, D. and Overmars, M. H. (2004). Useful
cycles in probabilistic roadmap graphs. In Proceed-
ings IEEE International Conference on Robotics &
Automation (ICRA), volume 1, pages 446–452.
Raveh, B., Enosh, A., and Halperin, D. (2011). A little
more, a lot better: Improving path quality by a path
merging algorithm. IEEE Transactions on Robotics,
27(2):365–371.
Reif, J. H. (1979). Complexity of the mover’s problem and
generalizations. In Proceedings Annual Symposium
on Foundations of Computer Science (SFCS), pages
421–427.
Rollinson, D. and Choset, H. (2011). Virtual chassis for
snake robots. In Proceedings IEEE International Con-
ference of IntelligentRobot and Systems (IROS), pages
221–226.
Song, G., Miller, S., and Amato, N. M. (2001). Customizing
prm roadmaps at query time. In Proceedings IEEE
International Conference on Robotics & Automation
(ICRA), pages 1500–1505.
Transeth, A. a., Pettersen, K. y., and Liljeb¨ack, P. (2009).
A survey on snake robot modeling and locomotion.
Robotica, 27(7):999–1015.
Tsianos, K. I., Sucan, I. A., and Kavraki, L. E. (2007).
Sampling-based robot motion planning: Towards real-
istic applications. Computer Science Review, 1:2–11.
Wein, R., van den Berg, J. P., and Halperin, D. (2005).
The visibility–voronoi complex and its applications.
In Proceedings Annual Symposium on Computational
Geometry (SCG), pages 63–72, New York, NY, USA.
ACM.
Zghal, H. and Dubey, R. V. ad Euler, J. A. (1990). Colli-
sion avoidance of a multiple degree of freedom redun-
dant manipulator operating through a window. In Pro-
ceedings IEEE American Control Conference, pages
2306–2312.
PlanningPracticalPathsforTentacleRobots
137
