Predicting Classifier Combinations
Matthias Reif
1
, Annika Leveringhaus
2
, Faisal Shafait
1
and Andreas Dengel
1
1
German Research Center for Artificial Intelligence, Trippstadter Strasse 122, 67663 Kaiserslautern, Germany
2
Department of Computer Science, University of Kaiserslautern, 67663 Kaiserslautern, Germany
Keywords:
Classifier Combination, Meta-learning, Meta-features, Classification, Classifier Ensembles.
Abstract:
Combining classifiers is a common technique in order to improve the performance and robustness of clas-
sification systems. However, the set of classifiers that should be combined is not obvious and either expert
knowledge or a time consuming evaluation phase is required in order to achieve high accuracy values. In
this paper, we present an approach of automatically selecting the set of base classifiers for combination. The
method uses experience about previous classifier combinations and characteristics of datasets in order to create
a prediction model. We evaluate the method on over 80 datasets. The results show that the presented method
is able to reasonably predict a suitable set of base classifiers for most of the datasets.
1 INTRODUCTION
According to Wolperts no-free-lunch theo-
rem (Wolpert, 1996), no single learning scheme
is able to generate the most accurate classifier for
any domain. There are three reasons why a learning
algorithm might fail for a given problem, that implies
a true hypothesis (Dietterich, 2000): (1) If not suffi-
cient training data is available, the learning algorithm
can find several hypotheses that approximate the true
hypothesis with the same accuracy. (2) Learning
algorithms might get stuck in local optima because
they often perform a local search to find the best
hypothesis. (3) The true hypothesis can not be
represented by any of the hypotheses that the learning
algorithm is able to create.
Because of these reasons, a suitable classifier for
a given domain is usually determined by either ex-
pert knowledge or an exhaustive evaluation of mul-
tiple algorithms. A different approach for avoiding
the failure of a single algorithm is to join multiple al-
gorithms. By combining the predictions of multiple
classifiers, the weaknesses of a single classifier in one
domain can be compensated by the strengths of a dif-
ferent classifier. Consequently, a combination of clas-
sifiers that are sufficiently accurate and diverse can
outperform single classifiers (Dietterich, 2000). Ad-
ditionally, by taking multiple classifiers into account,
the variance of the predictions is reduced and the ro-
bustness of the classification system can be increased.
The critical point on combining classifiers is sele-
cting the set of sufficiently accurate and diverse base-
level classifiers. If all classifiers deliver correlated
results, their combination would hardly provide any
improvement. Diversity among the base classifiers
can be introduced by using distinct algorithms, dif-
ferent parameter values of the same algorithm, dif-
ferent subsets of the samples, or different subsets of
the features. The fusion strategy defines how the out-
put of multiple classifiers are combined in order to
get one result. An appropriate fusion strategy can fur-
ther improve the performance of combined classifiers.
The fusion strategy might be serial, parallel, or hier-
archical. However, no type of combination has yet
been found that works best for all cases (Kuncheva
and Whitaker, 2003).
Also, the choice of classifiers that will be com-
bined has an influence on the final performance of the
classification system. An obvious approach would be
evaluating different set of classifiers and, finally, se-
lect the one that achieved the best results. Although
this probably will lead to good results, it is time con-
suming: Each considered classifier has to be trained,
preferable including a parameter optimization. In this
paper, we present an approach for automatically se-
lecting a suitable set of distinct classifiers for a given
dataset without the need of evaluating the classifiers.
The rest of the paper is structured as follows: In
the next section, we describe previous work. In the
following Section 3, the presented approach is ex-
plained in detail. Section 4 contains the evaluations.
The final Section 5 comprises a conclusion.
293
Reif M., Leveringhaus A., Shafait F. and Dengel A. (2013).
Predicting Classifier Combinations.
In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 293-297
DOI: 10.5220/0004266602930297
Copyright
c
 SciTePress

2 RELATED WORK
Meta-learning is used to make selections or recom-
mendations for new learning tasks. Knowledge about
previous learning tasks is modeled in order to gain
knowledge for the new learning task. A well known
example is algorithm selection: Based on the knowl-
edge about the best performing algorithm for multi-
ple datasets, a suitable algorithm is automatically se-
lected for a new dataset.
Typically, methods for algorithm or model selec-
tion are based on single algorithms, only, instead of
combinations of them. The best algorithm might
be predicted directly using classification (Bensusan
and Giraud-Carrier, 2000a; Ali and Smith, 2006),
a ranking approach creates a sorted list of all algo-
rithms (Brazdil et al., 1994; Brazdil et al., 2003; Vi-
lalta et al., 2004), or the actual accuracy of each con-
sidered algorithm is predicted using regression (Gama
and Brazdil, 1995; Sohn, 1999; Reif et al., 2012).
Only less work has been done in automatically
selecting suitable algorithm combinations based on
the given problem. (Cornelson et al., 2002) used
meta-learning to combine families of information re-
trieval algorithms. (Bennett et al., 2005) proposed a
probabilistic method for combining classifiers taking
context-sensitive reliabilities into account. (Todor-
ovski and D
ˇ
zeroski, 2003) presented meta decision
trees (MDT), that are used to decide which base clas-
sifier should be used to classify a sample. A MDT is
trained on the class probability distributions created
by the base classifiers for a given sample. However,
the set of used base classifiers has to be fixed in ad-
vance. (Kitoogo and Baryamureeba, 2007) investi-
gated the approach of selecting the best three out of
five base classifiers based on three dataset properties
(number of classes, number of attributes, and number
of samples). However, the approach does not auto-
matically select any classifiers but does a clustering
on the dataset properties and the performance values
of the different classifier combinations.
3 METHODOLOGY
In this paper, we investigate the approach of predict-
ing the best combination of three out of five classi-
fiers. The goal of the approach is to automatically
get a set of three classifiers for a given dataset which
combination achieves the highest possible accuracy.
Therefore, we fix the fusion strategy and use plurality
voting. We chose three classifiers because it is a good
compromise between the run-time and the diversity of
the classifiers. Additionally, using an odd number of
voting classifiers reduces the probability of ties.
The five base-level classifiers were selected that
their foundations make different assumptions. We
included tree-based and instance-based classifiers as
well as statistical classifiers and neural networks.
Each classifier includes an optimization of its most
important parameters using a grid-search and ten-fold
cross-validation. This means, whenever a classifier is
trained, its parameters are newly optimized. The se-
lected classifiers and their optimized parameters are:
k-Nearest Neighbor (k), MLP (learning rate), SVM
(γ, C), Decision Tree (confidence, minimal gain), and
Naive Bayes (laplace correction).
Like in most meta-learning approaches, datasets
are represented by their characteristics and properties.
Different measures are used to extract such proper-
ties, which are typically called meta-features. Obvi-
ous meta-features are the number of sample, the num-
ber of classes, and the number of attributes. Such sim-
ple meta-features are directly and easily extractable
from the dataset (Michie et al., 1994).
Besides simple measures with only limited de-
scriptive power, more sophisticated measures are used
as meta-features. We used meta-features from five
different groups: eight simple, five statistical (e.g.,
kurtosis, skewness, correlation) (Michie et al., 1994;
Castiello et al., 2005; Engels and Theusinger, 1998),
six information-theoretic (e.g., conditional entropy,
mutual information, signal-noise ratio) (Michie et al.,
1994; Segrera et al., 2008), 17 model-based (e.g.,
width and depth of a created decision tree) (Peng
et al., 2002; Bensusan et al., 2000), and eight land-
markers (e.g., accuracy of Naive Bayes, Nearest
Neighbor, and Decision Stumps) (Pfahringer et al.,
2000; Bensusan and Giraud-Carrier, 2000b). The
same 44 meta-features as used by (Reif, 2012) have
been calculated for each dataset.
The presented approach uses supervised-learning
for the prediction of a suitable set of classifiers.
Therefore, the training of the meta-learner requires
this information for each training dataset. First, the
dataset is preprocessed by replacing missing values
and converting nominal to numeric features because
SVM as well as MLP do not support nominal fea-
tures. Additionally, all features are normalized to the
interval [0;1]. Then, all base classifiers are trained on
the dataset using parameter optimization with a grid
search and a ten-fold cross-validation. Afterwards, all
ten possible combinations are evaluated by estimating
their performance using ten-fold cross-validation and
plurality voting. Finally, the combination maximizing
the accuracy is selected as label.
Since the collected meta-data is structured like a
traditional classification dataset, an arbitrary classi-
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
294

0
5
10
15
20
25
30
NB+KNN+MLP
NB+KNN+SVM
NB+MLP+SVM
KNN+MLP+SVM
DT+NB+KNN
DT+NB+MLP
DT+NB+SVM
DT+KNN+MLP
DT+KNN+SVM
DT+MLP+SVM
Number of datasets
best
solely
Figure 1: The number of datasets on which the different
classifier combinations achieved the highest accuracy – pos-
sibly with other combinations or solely.
fication algorithm can be applied on the meta-level.
Based on the previously created meta-dataset, it de-
livers a classification model that is able to predict a
suitable set of classifiers for a new dataset. We se-
lected a SVM as the meta-level learning scheme since
it has been successfully used in the past on a variety of
domains. However, we also tried different algorithms,
but we did not observe significant improvements com-
pared to SVM. Since the set of meta-features is rela-
tively big and the usefulness of each meta-feature is
not guaranteed, we applied forward selection (Kohavi
and John, 1997) of the features.
4 EVALUATION
We evaluated the approach on 84 datasets that were
randomly selected from UCI (Asuncion and New-
man, 2007), StatLib (Vlachos, 1998), and (Simonoff,
2003). They contain 2 to 24 classes, 1 to 359 features,
and 10 to 435 samples. The resulting meta-dataset
contains 84 samples, 44 features, and 10 classes.
As a preceding analysis, we counted how often
each combination is the best for a certain dataset be-
cause it achieves the highest accuracy. Additionally,
we determined how often a combination achieves the
highest accuracy for a dataset solely. The results are
shown in Figure 1. Two things are notable from this
plot: (1) The combination KNN+MLP+SVM seems to
be a good choice in general because it achieves the
highest accuracy most frequent, together with other
combinations but also solely. (2) Each combination
achieves the highest accuracy solely for at least two
datasets. This strengthens the necessity of select-
ing the set of used base classifiers depending on the
dataset.
Since the training data only consists of 84 sam-
ples, we applied a leave-one-out cross-validation for
evaluating the presented approach: For the prediction
of a classifier combination for a particular dataset, a
classification model based on the remaining 83 sam-
ples is trained. Afterwards, the predicted combina-
Accuracy
Best Prediction Average Best
0.0
0.2
0.4
0.6
0.8
1.0
Figure 2: Box plot of the accuracies achieved by using the
best combination, the averaged best combination, and the
predicted combination.
tion can be compared to the ground-truth information.
Since our meta-learning approach is a classification
task, typically classification measures such as classi-
fication accuracy might be used to evaluate the perfor-
mance of the prediction model. However, this would
lead to the following issues: If multiple combina-
tions achieve the highest accuracy, the label includes
only one of them and predicting any other combi-
nation with the same accuracy will lead to an error.
Also, predicting a sub-optimal combination with only
a slightly decreased accuracy as compared to the high-
est accuracy would receive the same error as predict-
ing the worst combination with a very low accuracy.
Therefore, we compared the accuracy achieved by the
predicted combination and the accuracy achieved by
the best combination.
Figure 2 shows a box plot of the accuracies
achieved by three strategies for selecting the classi-
fier combination: (1) the optimal combination achiev-
ing the highest possible accuracy, (2) the combina-
tion that achieved the highest average accuracy over
all datasets (KNN+MLP+SVM), and (3) the combination
predicted by the presented approach. Unfortunately,
just using the combination that worked best in aver-
age during the past seems to be a better strategy then
the presented approach.
For a deeper investigation of the results we also
looked at each dataset individually. Figure 3 shows
the accuracy achieved by the three strategies for each
dataset.
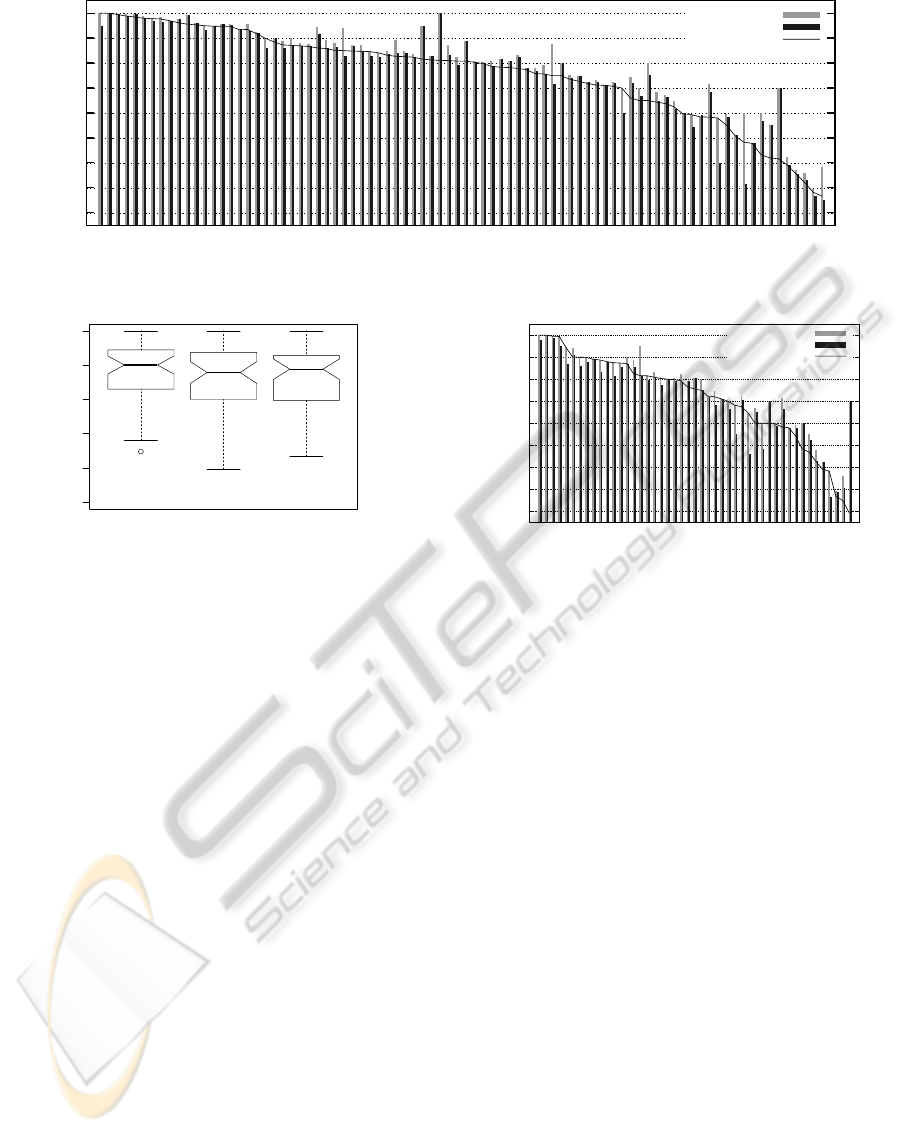
A first result is that the presented method achieves
the accuracy of the baseline or even the best accu-
racy for many datasets. For more than the half of
the datasets, the accuracy of the predicted combina-
tion is less than 2.5% smaller than the highest ac-
curacy. However, a second result from Figure 3 are
the small differences between the different selection
strategies for most of the datasets. Many datasets have
a very low variance within the different combinations.
While this fact is an indication of the robustness of
combining multiple classifiers, it also counteracts the
PredictingClassifierCombinations
295

0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Accuracy
Dataset
Best
Average Best
Prediction
Figure 3: The accuracy values achieved by the three methods for each dataset individually (sorted according to the accuracy
of the prediction for a better visualization).
Accuracy
Best Prediction Average Best
0.0
0.2
0.4
0.6
0.8
1.0
Figure 4: Box plot of the accuracies achieved by using the
best combination, the averaged best combination, and the
predicted combination for the reduced set of datasets.
meta-learning approach.
Learning to predict a good classifier combination
based on datasets with a very low variance over the
candidate combinations is problematic. It is hard
for the learning algorithm to create a discriminative
model if the training data is not discriminative itself.
Therefore, we investigated if using more discrimina-
tive combinations will improve the results. We cre-
ated a second meta-dataset that includes only knowl-
edge about base datasets with at least 5% accuracy
difference between the best and the worst classifier
combination. This was the case for 47 out of the 84
datasets. The reduced meta-dataset was used for both
training and testing. While removing particular sam-
ples from the training set is obviously valid, testing a
method on a reduced set might make the evaluation
less convincing. However, since we test our method
on datasets where the selection of the used base clas-
sifiers actually matters, we think that the evaluation is
still valid and convincing.
Figure 4 shows the box plot of the accuracies
achieved by the three strategies based on the reduced
dataset. It is visible that the performance of the pre-
sented method was improved compared to the base-
line method (“Average Best”). Unfortunately, a clear
benefit of the presented method is not noticeable.
Again, we plotted the accuracies achieved for each
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
Accuracy
Dataset
Best
Average Best
Prediction
Figure 5: The accuracy values achieved by the three meth-
ods for the reduced set of datasets (sorted according to the
accuracy of the prediction for a better visualization).
dataset individually, as shown in Figure 5. For most
of the datasets, the presented method was able to pre-
dict a classifier combination that is at least as good as
the baseline method. For some datasets, the predic-
tion is still worse than the baseline, especially for the
“parity5” dataset (rightmost in Figure 5). It is notable
that the presented method achieves even the highest
accuracy on over 20 of the 47 datasets.
5 CONCLUSIONS
In this paper we presented a novel approach for pre-
dicting the best classifier combination for a given
dataset. Based on dataset characteristics, the ap-
proach automatically selects three out of five base
classifiers that should be combined in order to achieve
high accuracy values on the dataset. Therefore, a
meta-learning approach was developed. A classifica-
tion model is trained based on the meta-features and
the knowledge about the optimal classifier combina-
tion for multiple datasets. The presented approach
was evaluated on 87 datasets. The results show the
overall suitability of the approach while its perfor-
mance could be increased if only datasets with diverse
combination accuracies were used for training.
ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods
296

REFERENCES
Ali, S. and Smith, K. A. (2006). On learning algorithm
selection for classification. Applied Soft Computing,
6:119–138.
Asuncion, A. and Newman, D. (2007).
UCI machine learning repository.
http://www.ics.uci.edu/∼mlearn/MLRepository.html
University of California, Irvine, School of Informa-
tion and Computer Sciences.
Bennett, P. N., Dumais, S. T., and Horvitz, E. (2005). The
combination of text classifiers using reliability indica-
tors. Information Retrieval, 8(1):67–100.
Bensusan, H. and Giraud-Carrier, C. (2000a). Casa batl is
in passeig de grcia or how landmark performances can
describe tasks. In Proc. of the ECML-00 Workshop on
Meta-Learning: Building Automatic Advice Strategies
for Model Selection and Method Combination, pages
29–46.
Bensusan, H. and Giraud-Carrier, C. (2000b). Discovering
task neighbourhoods through landmark learning per-
formances. In Proc. of the 4th Europ. Conf. on Princi-
ples of Data Mining and Knowledge Discovery, pages
325–330.
Bensusan, H., Giraud-Carrier, C., and Kennedy, C. (2000).
A higher-order approach to meta-learning. In Proc. of
the ECML’2000 workshop on Meta-Learning: Build-
ing Automatic Advice Strategies for Model Selection
and Method Combination, pages 109–117.
Brazdil, P., Gama, J., and Henery, B. (1994). Characteriz-
ing the applicability of classification algorithms using
meta-level learning. In Machine Learning: ECML-94,
volume 784 of Lecture Notes in Computer Science,
pages 83–102. Springer Berlin / Heidelberg.
Brazdil, P. B., Soares, C., and da Costa, J. P. (2003). Rank-
ing learning algorithms: Using IBL and meta-learning
on accuracy and time results. Machine Learning,
50(3):251–277.
Castiello, C., Castellano, G., and Fanelli, A. M. (2005).
Meta-data: Characterization of input features for
meta-learning. In Modeling Decisions for Artificial
Intelligence, volume 3558, pages 295–304. Springer
Berlin / Heidelberg.
Cornelson, M., Grossmann, R. L., Karidi, G. R., and Shnid-
man, D. (2002). Survey of Text Mining: Cluster-
ing, Classification, and Retrieval, chapter Combining
Families of Information Retrieval Algorithms using
Meta-Learning, pages 159–169. Springer.
Dietterich, T. G. (2000). Ensemble methods in machine
learning. In Proc. of the First Int. Workshop on Multi-
ple Classifier Systems, pages 1–15.
Engels, R. and Theusinger, C. (1998). Using a data metric
for preprocessing advice for data mining applications.
In Proc. of the Europ. Conf. on Artificial Intelligence,
pages 430–434.
Gama, J. and Brazdil, P. (1995). Characterization of clas-
sification algorithms. In Progress in Artificial Intelli-
gence, volume 990 of Lecture Notes in Computer Sci-
ence, pages 189–200. Springer Berlin / Heidelberg.
Kitoogo, F. E. and Baryamureeba, V. (2007). Meta-
knowledge as an engine in classifier combination. In-
ternational Journal of Computing and ICT Research,
1(2):74–86.
Kohavi, R. and John, G. H. (1997). Wrappers for feature
subset selection. Artificial Intelligence – Special issue
on relevance, 97:273–324.
Kuncheva, L. I. and Whitaker, C. J. (2003). Measures
of diversity in classifier ensembles and their relation-
ship with the ensemble accuracy. Machine Learning,
51(2):181–207.
Michie, D., Spiegelhalter, D. J., and Taylor, C. C. (1994).
Machine Learning, Neural and Statistical Classifica-
tion. Ellis Horwood.
Peng, Y., Flach, P., Soares, C., and Brazdil, P. (2002). Im-
proved dataset characterisation for meta-learning. In
Discovery Science, volume 2534 of Lecture Notes in
Computer Science, pages 193–208. Springer Berlin /
Heidelberg.
Pfahringer, B., Bensusan, H., and Giraud-Carrier, C. (2000).
Meta-learning by landmarking various learning algo-
rithms. In Proc. of the 17th Int. Conf. on Machine
Learning, pages 743–750.
Reif, M. (2012). A comprehensive dataset for evaluating
approaches of various meta-learning tasks. In First
International Conference on Pattern Recognition and
Methods.
Reif, M., Shafait, F., Goldstein, M., Breuel, T., and
Dengel, A. (2012). Automatic classifier selection
for non-experts. Pattern Analysis and Applications.
10.1007/s10044-012-0280-z.
Segrera, S., Pinho, J., and Moreno, M. (2008). Information-
theoretic measures for meta-learning. In Hybrid Ar-
tificial Intelligence Systems, volume 5271 of Lecture
Notes in Computer Science, pages 458–465. Springer
Berlin / Heidelberg.
Simonoff, J. S. (2003). Analyzing Categor-
ical Data. Springer Texts in Statis-
tics. Springer Berlin / Heidelberg.
http://people.stern.nyu.edu/jsimonof/AnalCatData/.
Sohn, S. Y. (1999). Meta analysis of classification al-
gorithms for pattern recognition. IEEE Transac-
tions on Pattern Analysis and Machine Intelligence,
21(11):1137 –1144.
Todorovski, L. and D
ˇ
zeroski, S. (2003). Combining clas-
sifiers with meta decision trees. Machine Learning,
50:223–249.
Vilalta, R., Giraud-Carrier, C., Brazdil, P., and Soares, C.
(2004). Using meta-learning to support data mining.
International Journal of Computer Science and Appli-
cations, 1(1):31–45.
Vlachos, P. (1998). StatLib datasets archive.
http://lib.stat.cmu.edu Department of Statistics,
Carnegie Mellon University.
Wolpert, D. H. (1996). The lack of a priori distinctions
between learning algorithms. Neural Computing,
8(7):1341–1390.
PredictingClassifierCombinations
297