
A Maintenance-optimal Swapping Policy
For a Fleet of Electric or Hybrid-electric Vehicles
Ahmad Almuhtady
1
, Seungchul Lee
1
, Edwin Romeijn
2
and Jun Ni
1
1
Deapartment of Mechaincal Engineering, University of Michigan, Ann Arbor, U.S.A.
2
Department of Industrial and Operations Engineering, University of Michigan, Ann Arbor, U.S.A.
Keywords: Resource Allocation Policy, Swapping Policy, Branch and Bound, Intelligent Maintenance.
Abstract: Motivated by high oil prices, several large fleet companies initiated future plans to hybridize their fleets to
establish immunity for their optimized business models against severe oil price fluctuations, and adhere to
increasing awareness of environmentally-friendly solutions. The hybridization projects increased
maintenance costs especially for highly costly and degradable components such as Li-ion batteries. This
paper introduces a degradation-based resource allocation policy to optimally utilize batteries on fleet level.
The policy, denoted as Degradation-based Optimal Swapping Policy, incorporates optimal implementation
of swapping and substitution actions throughout a plan of finite time horizon to minimize projected
maintenance costs. The swapping action refers to the inter-change in the placement of two batteries within a
fleet. The substitution action refers to the replacement of degraded batteries with new ones. The policy takes
advantage of the different degradation rates in the batteries health states; due to different loading conditions;
achieving optimal placement at different time intervals throughout the plan horizon. A mathematical model
for the policy is provided. The optimization of the generated model is studied through several algorithms.
Numerical results for sample problems are shown to illustrate the capability of the proposed policy in
establishing substantial savings in the projected maintenance costs compared to other policies.
1 INTRODUCTION
While Oil prices throughout the last decades have
undergone significant increases, transportation still
in general relies on it for 97% of its energy. It
becomes significantly harder for companies and
corporations with large fleets to maintain their
preferred higher profit margins. Therefore, many of
these fleet companies were highly motivated to
reduce their annual fuel consumption which reflects
on millions of dollars in savings. Additionally,
environmentally friendly technologies have attracted
large companies and corporations who benefit from
both commercial advertisement of endorsing such
technologies and established savings. For example,
Wal-Mart has set a goal of doubling the fleet
efficiency by 2015 from a 2005 baseline. One aspect
of these plans has included the consideration of
hybridizing fleets to enhance the fuel economy. Both
FedEx and UPS have as well endorsed hybridizing
parts of their fleets. Environmentally conscious
cities, schools and universities (e.g. University of
Michigan) have as well introduced hybrid-electric
buses into their fleets.
In a hybrid system, batteries have the most
significant share of the total cost of the hybrid
system. These components degrade to a point where
substitution with new ones becomes inevitable. The
substitution action here is defined as the replacement
of the degraded battery with a new one. The limited
battery useful life motivates the consideration of
maintenance plans which can incorporate a
predictive scheme of batteries health states. This
plan will reduce the projected battery maintenance
costs and ensure less abruptly interrupted daily task
assignment to these hybrid vehicles. Fair prediction
of the battery degradation within commercial fleets
is attainable due to the consistency in the expected
work load. For example, in a fleet of delivery trucks,
the batteries in hybrid vehicles assigned to
Downtown area routes are most likely subjected to
larger frequencies of micro charging and discharging
cycles in comparison to those within vehicles
assigned to the suburbs. This reflects significantly
on the degradation rate of these batteries. This
consistency can help a predictive maintenance
policy to optimally utilize all the batteries on fleet
35
Almuhtady A., Lee S., Romeijn E. and Ni J..
A Maintenance-optimal Swapping Policy - For a Fleet of Electric or Hybrid-electric Vehicles.
DOI: 10.5220/0004270601830192
In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 183-192
ISBN: 978-989-8565-40-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

level. To achieve this, a uniquely formulated policy,
designated as Degradation-based Optimal Swapping
(DBOS) policy, is proposed in this paper.
In most current companies which run hybrid
vehicles in their fleets, batteries are used until they
reach retirement. However, swapping batteries
within their fleet can achieve a reduction in the
projected cost of the maintenance plans. The
swapping action here is defined as the inter-change
in the placement of two batteries from two different
loading (degradation) profiles. This swapping policy
relies on the prediction of the different degradation
rates which is attributed mainly to the loading and
usage conditions. The prediction of such degradation
level introduces a potential to conduct swapping
actions among batteries and to control the timing of
the end of life for these batteries, where substitution
becomes inevitable. One direct impact of this is
providing substantial savings in projected
maintenance costs as a result of the application of
such policy. Additionally, this policy has the
potential to provide an integration between
maintenance actions and the company's daily
operations (integration of maintenance and
logistics). This enables a sustainable management of
the costly hybrid fleet asset. Additionally, the
information obtained throughout the policy can be
invested to build up a database of retired batteries in
terms of their conditions and predicted date of
retirement. This database can significantly improve
the success of the retired batteries remanufacturing
schemes, already implemented in several OEMs.
The remanufacturing helps both reduce the
environmental impact resulting from the disposal of
such batteries and promotes the use of cheap second-
hand hybrid technologies.
The research in this paper includes the
development of the model to describe the policy in
its general form and the investigation of suitable
approaches to achieve the optimum solution. The
remainder of this paper is organized as follows.
Section 2 will review relevant research work.
Section 3 will focus on modeling the policy in a
comprehensive mathematical model which accounts
for all the decision variables necessary to apply the
policy. The solution to the generated model
including the development of a policy-specific
optimization algorithm will be the focus of Section
4.
2 LITERATURE REVIEW
This problem can be categorized under the planning
and scheduling optimization, as the generated output
could be in the form of a schedule of different
placements for the batteries within the fleet. Both
planning and scheduling deal with the allocation of
available resources over time to perform a collection
of tasks. The difference between planning and
scheduling is not always clear cut (Grossmann et al.,
2002). However, in general planning deals with
longer time horizons (e.g. weeks, few months) and it
deals with high level decisions such as investment in
new facilities and production levels. Scheduling on
the other hand is concerned with shorter time
horizons (e.g. days, few weeks) with the emphasis
often being on the lower level decisions such as
sequencing of operations. Although the expected
outcome decisions from the DBOS policy are low
level decisions such as the change of the placement
of a battery, DBOS is intended to be part of a long
maintenance plan horizon. Therefore the policy can
be classified under either scheduling or planning.
DBOS model is expected to partially share the
form of one of the most famous scheduling problems
which is globally known as the fleet assignment
problem in transportation science. Given a flight
schedule and a set of aircraft of different types, the
fleet assignment problem faced by an airline is to
determine which type of aircraft should fly each
flight segment on the airline’s daily (or weekly)
schedule (Bertsimas and Tsitsiklis, 1997). The
similarity between these two problems mainly arises
in the placement decision variable; chosen to be
binary in many cases; this variable holds the key to
optimize the objective function. In the fleet
assignment problem, there are several factors
considered in assigning a fleet to a flight leg. These
factors include passenger demand, revenue, seating
capacity, fuel costs, crew size, availability of
maintenance at arrival and departure stations, gate
availability, and aircraft noise. Many of these factors
are captured in the objective coefficient of the
decision variable; others are captured by constraints
(Hane et al., 1995). On a similar basis, modelling the
problem for the DBOS policy is intended to take into
account several factors, such as degradation profiles,
demand, health states tracking, maintenance
capabilities and costs associated with the swapping
and substitution actions. However, there are several
important differences between the two problems
such as the substitution variables (reset variables)
needed for DBOS to function properly. The
substitution variables interaction with the placement
variables and their major contribution in the
objective function uniquely characterizes DBOS.
The fleet assignment problem has been studied
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
36

by numerous researchers. The daily scheduling of
the fleet assignment problem formulation impose
large number of integer variables and severely
degenerate model which leads to poor performance
of standard linear programming techniques. Methods
to address this problem include an interior-point
algorithm, dual steepest edge simplex, cost
perturbation, model aggregation, branching on set-
partitioning constraints, and prioritizing the order of
branching (Hane et al., 1995). In (Talluri, 1996), a
model and an algorithm for swapping applications in
a daily airline fleet assignment have been developed.
Given a daily fleet assignment, the problem of
changing the assignment of a specified flight leg to a
different equipment type while still satisfying all the
constraints have been considered. As airline
planning process evolves through several decision
making phases including schedule construction and
fleet planning that are succeeded by aircraft
maintenance routing and crew scheduling, the need
for integrated planning and robust planning were
realized. Integrated planning is intended to integrate
the functional phases at the planning stage, and
robust planning is intended to make decisions at the
planning stage that are beneficial to the operations
(Gao et al., 2009). Integrating schedule design and
fleet assignment was implemented in (Rexing et al.,
2000); (Lohatepanont and Barnhart, 2004).
Examples of research on robust planning include
robust fleet assignment as in (Rosenberger et al.,
2004); (Smith and Johnson, 2006).
Planning and scheduling problems generally
incorporate discrete/continuous optimization
problems. The mixed integer nonlinear program
(MINLP), inherently require special treatment as
complexities arise due to nonlinearity and integer
choices. The most common MINLPs encountered in
planning are 0-1 integer nonlinear programming
(ZOINLP) problems where none of the continuous
variables exist and all the decision variables are
binary. As section 3 of this paper details the
modelling of the DBOS policy, it will become
apparent that the generated model falls under
(ZOINLP) problems category.
The basis of tackling integer programming
problems (whether linear or nonlinear) in many
algorithms rely on relaxing the problem into
continuous sub-problems. The algorithm in this case
works on a higher level establishing control on the
sub-solvers and using the information from the sub-
problems solutions to arrive to the integer solution.
The sub-problems are solved by some well-
performing continuous variable programming
problem solver (such as Simplex for linear
programming (LP) problems (Chvátal, 1983) and
Sequential Quadratic Programming (SQP) with
reduced gradient method (Schittkowski, 1982) for
nonlinear programming (NLP) problems). Branch
and Bound (B&B) algorithm (Gupta and Ravindran,
1985) falls under this category of integer
programming problem solvers. B&B consists of a
tree enumeration in which LP or NLP sub-problems
are solved at each node, and eliminated based on
bounding properties. B&B’s success and speed in
finding the solution inherently depends on the
relaxed problem sub-solver.
Other algorithms for solving MINLP include
Generalized Benders Decomposition (GBD)
(Benders, 1962); (Geoffrion, 1972), Outer-
Approximation (OA) (Duran and Grossmann, 1987);
(Fletcher and Leyffer, 1994), and Extended Cutting
Plane Method (ECP) (Westerlund and Pettersson,
1995). The literature also provides some non-
rigorous methods for handling non-convexities such
as the equality relaxation algorithm (Kocis and
Grossmann, 1987) and the augmented penalty
version of it by (Viswanathan and Grossmann,
1990). Modifications on standard Stochastic
methods such as Genetic Algorithm (GA) originally
developed by (Holland, 1975) and Simulated
Annealing (SA) originally developed by (Metropolis
et al., 1953) have promoted their use to solve
MINLPs. These algorithms impose no limitation
(such as continuity and differentiability) on the
search space of the optimization problem.
Additionally, some of these algorithms could benefit
from parallel processing which in turn accelerates
convergence. Hybrid algorithms as in (Adler, 1993);
(Robinson et al., 2002); (Xia and Wu, 2005) are as
well widely found in Literature. Such algorithms
intend to take advantage of the merits of two or
more of the standard algorithms to achieve better
solutions (in terms of convergence, global optima,
etc.).
3 MATHEMATICAL
MODELLING OF DBOS
POLICY
The key to apply the DBOS policy is a concise and
representative model which accounts for swapping
and substitution actions. The objective of the policy
aims towards optimal battery utilization over a finite
plan horizon in a way that minimizes total
maintenance plan projected costs.
Typical constraints are formulated for demand
AMaintenance-optimalSwappingPolicy-ForaFleetofElectricorHybrid-electricVehicles
37

(number of vehicles operating in each degradation
profile), batteries health state degradation tracking
(swapping and substitution effects, threshold, etc.)
(See Figure 1). Other constraints are relevant to the
company’s logistics such as maintenance crew
availability, business requirements, etc. The model
includes two types of decision variables: placement
variables and substitution variables (or reset
variables).
Figure 1: Health State Changes with Swapping and
Substitution Actions.
3.1 Placement Decision Variables
The model is formulated to follow the placement of
batteries in terms of location and time. The location
here refers to the loading profile in which the battery
is placed, and for which predicted degradation rate
of the health state is assumed to be known. The
variable is studied at predefined constant discrete
intervals of time (Δ), which are chosen upon the
company’s preference and capability to achieve
regular workflow. This interval should be inspired
by the company’s prescheduled checkups cycles. For
example if the company’s vehicles are usually
maintained or checked up monthly, then choosing Δ
to be equal to 1 month is reasonable. Δ relates the
frequency of the discrete time points at which the
scheduler has the option to perform a swapping
action. Theoretically as ∆ gets smaller, more
swapping options are present and we expect the total
maintenance cost to decrease to a certain limit. This
limit is where introducing further swapping actions
will not improve the cost function and the optimizer
opts for no additional swapping actions upon correct
implementation of the policy (accurate
optimization). The validation of such behaviour is
shown in Section 4.3.
In this formulation, the placement decision
variable,
() 0,1
ij
Xk
in the model is chosen to be
binary, where its indices stand for
1,2, , battery index in the fleet
1, 2, , degradation/loading profile
1,2, , discrete time, where:
plan horizon
in
jm
kK
KT
(1)
For example, if Δ = 1 month, and X
31
(7) = 1 means
that the 3
rd
battery is placed in the first degradation
profile at the 7
th
month.
There are several constraints which are related
directly to the placement decision variable. Some of
these constraints arise from physical sense, others
from demands and capabilities. The first constraint
relates to the physical sense that a specific battery
can be only assigned to one degradation profile for a
specific interval. Additionally, the demand
j
d
drives the number of batteries assigned to the jth
degradation profile per interval. In formulation,
these two constraints; respectively; translate to:
1
1
( ) 1, 1, , ; 1, ,
() , 1, , ; 1, ,
m
ij
j
n
ij j
i
X
kinkK
X
kd j m k K
(2)
The placement variable is the indirect indicator for
whether a swapping action has taken place or not.
This can be formulated through:
if the th battery is
1 swapped at time to/from
() ( 1)
the th degradation profile
0 otherwise
ij ij
i
k
Xk Xk
j
(3)
The total number of swapping actions which take
place at time k can be given by:
11
1
() ( 1)
2
nm
ij ij
ij
Xk Xk
(4)
Equation (4) enables us to formulate the constraints
related to the company’s preferential rules for
swapping. Examples of these rules include an
enforced minimum span between subsequent
swapping actions for the same battery, and
maximum number of allowable swapping actions
within the fleet per interval. For the first one, if Δ is
assumed to be equal to 1 month (for example), and a
minimum of 3 months of enforced span between
subsequent swapping actions for the same battery,
then it translates to:
11
1
11
() ( 1) ( 1) ()
22
1
(2) (1)1,
2
1, , ; 2, ,
mm
ij ij ij ij
jj
m
ij ij
j
X
kXk Xk Xk
Xk Xk
ink K
(5)
0.7
0.75
0.8
0.85
0.9
0.95
1
0 2000 4000 6000
DegradationIndicator
Time
∆ ∆ ∆∆
Swapping
effect
Substitution
effect
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
38

Or it can be abbreviated as:
2
01
1
() ( 1)1,
2
1, , ; 2, ,
m
ij ij
hj
Xkh Xkh
ink K
(6)
In the general form, the constraint can be
represented as (for a minimum span of
H
between swapping actions for the same battery):
1
01
1
() ( 1)1,
2
1, , ; 2, ,
Hm
ij ij
hj
Xkh Xkh
ink K
(7)
Maximum number (
) of swapping actions per
interval can be easily modelled as:
11
1
() ( 1) , 2, ,
2
nm
ij ij
ij
X
kXk k K
(8)
3.2 Substitution Decision Variables
A substitution decision variable,
()
i
Z
k
to represent
any substitution action is included in the modelling.
if the th battery is substituted
1
at the begining of epoch
()
no substitution at the
0
begining of epoch
i
i
k
Zk
k
(9)
The substitution variable has only two indices as it
relates only to battery i being substituted and time k
at which substitution takes place.
The decision whether to initiate a substitution
action or not, is merely dependent on the state of the
battery health. This indicates the need to track the
battery’s health state degradation throughout its
deployment in the field. In modelling DPSO with
deterministic states, it is assumed that the degradable
health states are predictable. The prediction is
dependent on both the battery state at the beginning
of the current interval and the degradation profile at
which the battery is placed.
To track the degradation of the batteries health
states, an accumulative degradation dependent
quantity
()
i
yk
is defined. The accumulative
degradation is a monotonically increasing dependent
variable which is calculated in the model based on
the decision variables (placement and substitution
variables). In this formulation, when a new battery is
brought in, the accumulative degradation is set to
zero. Based on the assumption of linear degradation
the accumulative degradation can be found by:
1
1
1
(0) 0 1, ,
() 1 () ( 1) ()
() ()
1(1) (),
1, , ; 1, ,
i
m
iii jij
j
m
ijij
j
m
ik i j ij
j
yin
yk Zk yk rX k
Zk rX k
Zyk rXk
kKin
(10)
where
j
r
is the degradation rate when the battery is
assigned to jth degradation profile.
Additional constraints arise from the bounds on
the accumulative degradation variable:
0(),
1, , ; 1, ,
i
yk
kKin
(11)
where
is the threshold at which substitution
becomes inevitable.
3.3 Objective Function
There are several objectives that could be used
towards an optimum policy. The policy can aim for
minimized maintenance costs, maximized utilization,
or a combination of both. One direct and simplified
objective that can be chosen is to minimize the
projected maintenance costs over a finite plan
horizon. With the satisfaction of the constraints
described above, the minimization of the projected
costs which are attributed to the batteries
substitution and swapping actions can achieve an
optimum scheduling policy. Based on the discussion
previously, the cost can be found by:
1
211
2
11
1
() () ( 1)
2
() ()
Knm
ij ij
kij
nK
i
ik
JckXkXk
ckZk
(12)
where c
1
(k) is time dependent swapping cost
coefficient, which includes penalties and potential of
loss due to swapping, and c
2
(k) is time dependent
substitution cost coefficient. The choice to make
both cost coefficients as time dependent increases
the flexibility of the model.
AMaintenance-optimalSwappingPolicy-ForaFleetofElectricorHybrid-electricVehicles
39
4 OPTIMIZATION IN DBOS
POLICY
The mathematical model of DBOS policy with
deterministic states has been introduced in Section 3.
This section is dedicated to the solution of the
DBOS policy model.
4.1 DBOS-Policy-specific
Branch-and-Bound-based
Algorithm
Although the generated model successfully captures
the intended functionality of the policy, the DBOS
policy model is a Zero-One Integer Nonlinear
programming (ZOINLP) problem. In similar work
(Almuhtady et al., 2012), typical stochastic
algorithms such as Genetic Algorithm (GA) and
Simulated Annealing (SA) Algorithm have been
shown to be capable of solving small size problems
of this type. However, repeatability in results and
robustness for large scale problems were absent in
the implementation. Additionally, the
implementation of a direct Branch and Bound (B&B)
scheme with variant NLP sub-solvers has not been
successful due to the growing nonlinearity in health
state updates in Equation (10).
In this paper, we introduce a DBOS-policy-
specific Branch-and-Bound-based algorithm that
successfully generates repeatable answers as well as
provide robustness over all problem sizes. The
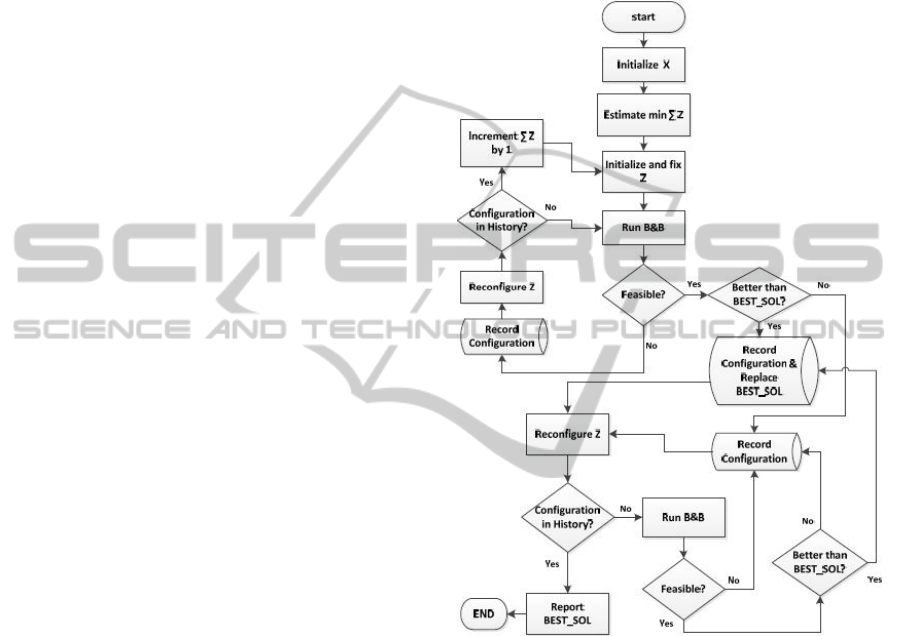
algorithm is illustrated in Figure (2).
The algorithm reduces the complexity of the
model by providing incremented estimates of the
total number of required substitutions (Z
i
(k)). The
estimates are generated from expected loads and
logic-based rules. Total demand over horizon (when
averaged per battery) dictates whether this estimate
is started at zero or not. For example, if the average
demand per battery exceeds threshold value (),
starting with estimate (Z
i
(k)=0) becomes trivial.
For each estimate, all satisfying (non-repeated)
configurations are investigated. The reconfiguration
is done systematically that it will generate each time
a new configuration until all possible unrepeated
configurations for that estimate have been tested.
We note here that repeated configurations include
any new Z
i
(k) array that is generated from swapping
rows in an old Z
i
(k) array as this action provides no
new configurations. The first estimates are chosen to
be very conservative (low number of substitutions).
This probably leads to infeasibility for all or most
reconfigurations of Z
i
(k) for the first iteration.
Nevertheless, the conservativeness provides
assurance for minimum objective value function as
the major part of the cost is attributed to the
substitution. We note here that the infeasibility is
identified quickly and therefore the performance of
the algorithm in general is not hindered by the
conservativeness.
Figure 2: DBOS-Policy-Specific Branch-and-Bound-based
Algorithm.
With this implementation, at each instant the
nonlinearity in the model (Equation 10) ceases to
exist and the problem is reduced to a Zero-One
Integer Linear Programming (ZOILP) problem. This
promotes the utilization of a Branch and Bound
(B&B) scheme with a (LP) sub-solver. The later
only applies if the absolute value in the objective
function is formatted in the standard LP form as well.
This is easily implemented through a number of
well-known mathematical tricks. It should be noted
that the formatting of the absolute value into the
standard LP form incorporates an increase in the
decision variables which may adversely affect the
algorithm’s performance for significantly large
problems.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
40

4.2 Case Study I
In this section, we report numerical results of a 5-
vehicle fleet case study. The problem parameters are
available in Table (1).
Table 1: Case Study I Parameters.
Parameter symbol value
N
umber of vehicles N 5
N
umber of loading profiles M 4
Plan Horizon (months) K
4
vehicles allocated per loading profile
J
N
[1, 1, 1, 2]
Degradation rates (per month)
j
r
[0.11, 0.08, 0.04,
0.02]
Swapping Cost Coefficient
1
()ck
400
Substitution Cost Coefficient
2
()ck
11600
Threshold β 0.2
Discretization Interval (month) ∆ 1
The cost coefficients are inspired by real
applications. The degradation coefficients have been
modified to reflect shorter chosen plan horizon for
the numerical case study as a sample problem. The
modification in the coefficients is intended to
simulate the real scenario where longer horizons are
chosen, and thus substitutions are inevitable.
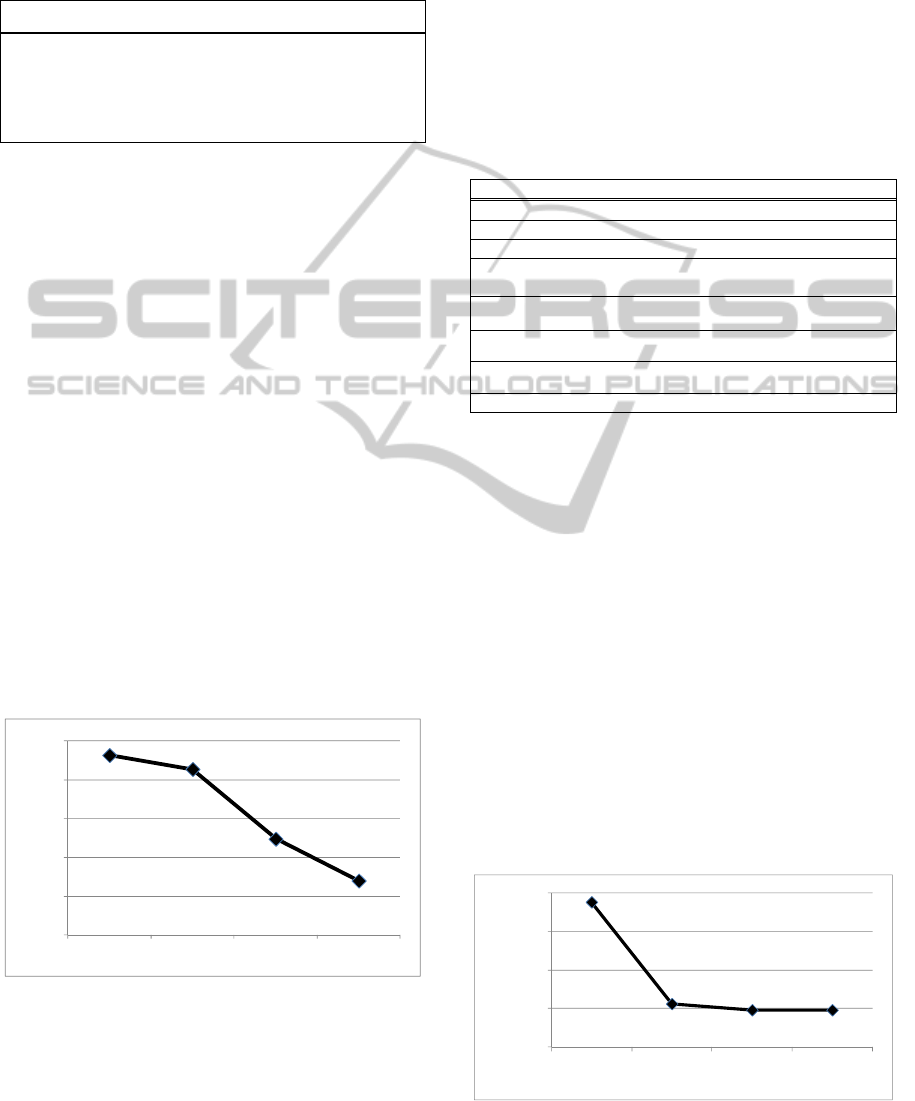
The solutions generated by GA and SA are
shown in Figures (3) and (4). The horizontal line
indicates the cost upon the application of no
swapping policy for the case study. Though SA
outperforms GA in this case, repeatability in results
and lack of runs achieving the global minima are
shortcomings of both algorithms. The runtimes for
GA and SA algorithms were 19 minutes and 45
seconds; respectively.
The solutions generated by DBOS-policy-
specific B&B-based algorithm are shown in Figure
(5). It is clear that the repeatability has been attained
only in the DBOS-policy-specific B&B-based
algorithm where global optima have been achieved
at every single run. The runtime was found to be 41
minutes.
Though repeatability might not represent great
significance in this small size problem as SA can be
run cheaply several times, there are two main
advantages of using DBOS-policy-specific B&B-
based algorithm. The first is that the total cost
associated by the swapping and substitution actions
is $14000 with the DBOS-policy-specific algorithm
in comparison to the best run of SA with cost equal
to $14800. That means SA best run has generated a
suboptimal solution with 5.4% difference. The
guarantee of achieving the global minima with the
proposed algorithm is a key for its outperformance.
That is, for this small problem, the difference in cost
between SA best run and the proposed algorithm
solutions are 5.4%. This can be higher for a different
problem. The second advantage will be present in
the scalability as Case Study II will show.
Specifically, the case study will demonstrate what
the outcomes are when larger numbers of decision
variables are involved.
Figure 3: GA Different Runs.
Figure 4: SA Different Runs.
Figure 5: DBOS-Policy-specific B&B-based Algorithm
Different Runs.
0
10000
20000
30000
40000
50000
60000
0 102030
Cost
run
noswapping
cost
0
10000
20000
30000
40000
50000
0 102030
Cost
run
noswapping cost
0
10000
20000
30000
40000
50000
0510
Cost
run
noswapping cost
AMaintenance-optimalSwappingPolicy-ForaFleetofElectricorHybrid-electricVehicles
41
The optimum schedule per DBOS policy for Case
Study I is shown in Table (2).
Table 2: Schedule of Batteries Placement from the DBOS-
Policy-specific B&B-based Algorithm.
Battery 1st month 2nd month 3rd month 4th month
A 4 4 4 1
B 2 1 1* 2
C 4 2 2 4
D 3 3 3 3
E 1 4 4 4
(*) means a substitution action has taken place
Finally for case study I, we benchmark the
performance of the DBOS policy, several
management policies have been applied (see Figure
6).
The maintenance plan cost has been evaluated
for each of the four shown policies. In the “No-
swapping” policy, the batteries in the fleet are
dedicated to one degradation profile throughout the
plan horizon, where no swapping is allowed. The
rotational fixed swapping policy refers to the policy
where swapping actions are conducted on a timely,
fixed and cyclic manner. An example of that is the
rotational swapping of tires in automobiles to even
out the degradation (front wheel driving or rear
wheel driving). The third policy (Intelligent fixed
swapping) refers to the case when swapping actions
are conducted between the most and the least
degraded batteries at each cycle (The intelligence
refers to basing decision on being informed about
the health state of the battery). Though the later
performs better than the No-swapping and
Rotational Fixed Swapping policies, the DBOS
policy clearly outperforms all of them.
Figure 6: Benchmarking DBOS policy.
4.3 Case Study Ii (∆ Variation)
In this section, we verify the claim we made in
Section 3.1 about the role of ∆. The DBOS-policy-
specific branch-and-bound-based algorithm is
implemented on a second case study (see Table 3)
where ∆ is varied from 1 week to 1 month. The case
study will serve as well to illustrate the scalability of
the proposed algorithm when larger numbers of
decision variables are involved. That is, decreasing
∆ increases the size of the problem significantly due
to the increase in the placement and substitution
variables under investigation. The outcome of this
increase on the performance of SA and the proposed
policy is investigated.
Table 3: Case Study II Parameters.
Parameter symbol value
Number of vehicles N 3
Number of loading profiles M 2
Plan Horizon (months) K
4
vehicles allocated per loading
profile
J
N
[1, 2]
Degradation rates (per month)
j
r
[0.11, 0.04]
Swapping Cost Coefficient
1
()ck
400
Substitution Cost Coefficient
2
()ck
11600
Threshold β 0.2
Figure (7) shows the results when SA was used.
It can be seen that SA algorithm is unable to capture
the intended behaviour of the DBOS policy. The
policy aims to opt for swapping when swapping
achieves decreased objective values. In this case, as
the problem size grows the optimizer fails to
recognize the unnecessary swapping actions and
therefore the total cost increases. On the other hand,
Figure (8) shows the results of the DBOS-policy-
specific B&B-based algorithm when ∆ is varied. The
anticipated behaviour appears clearly. The cost
decreases when ∆ is varied from 1 month, to 20 days
and finally to half month. After that, there is no
improvement in the objective value when ∆ is
shortened from 15 days to 1 week. The optimizer in
this case opts for no more swapping actions than
what has been chosen for the 15 days discretization
interval, and therefore the policy is correctly
captured.
Figure 7: SA algorithm best run result when ∆ is varied.
0
100
200
300
400
500
Noswapping RotationalFixed
Swapping
IntelligentFixed
Swapping
DBOS
Cost
x10
2
20000
25000
30000
35000
40000
1week 15days 20days 1month
Cost
∆
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
42
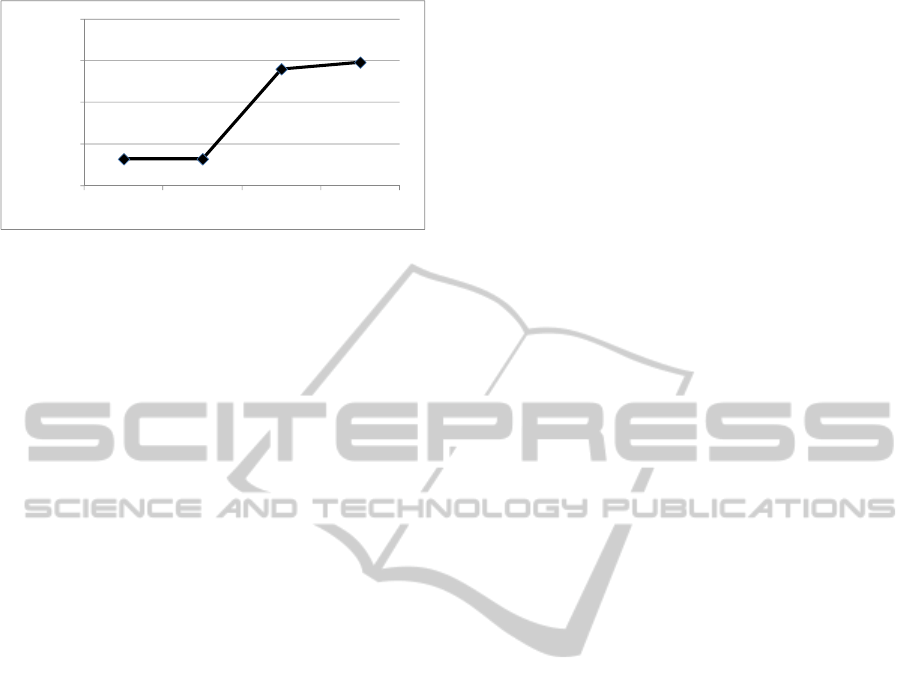
Figure 8: DBOS-policy-specific B&B-based algorithm
result when ∆ is varied.
5 CONCLUSIONS
Plans for electrification and hybridization of fleets
are already in progress to minimize the overall cost
of operation and fuel consumption and adhere to
environmentally friendly awareness. The
hybridization projects increased maintenance costs
especially for highly costly and degradable
components such as Li-ion batteries. This paper
presented a uniquely formulated resource allocation
policy based on the degradation of the health states
of the batteries, to be part of the maintenance
planning for the fleet. The policy, denoted as
Degradation-based Optimal Swapping (DBOS),
utilizes batteries on fleet level through a series of
optimally chosen swapping and substitution actions.
The policy takes advantage of the different
degradation rates of the batteries within the fleet,
based on loading conditions, to choose optimal
placements of these batteries. A representative
mathematical model with deterministic health states
have been presented in this paper as well. The
optimization of the generated model of DBOS policy
has been investigated as well. A DBOS-policy-
specific algorithm has been developed and
successfully implemented. Numerical results showed
the outperformance of the algorithm in comparison
to standard optimization techniques. Numerical
results as well validated the role of the discretization
interval in the DBOS policy, allowing but not
necessary choosing the option to perform additional
swapping actions minimizing the costly substitution
ones.
ACKNOWLEDGEMENTS
This material is based upon work supported by the
National Science Foundation under Grant No.
0639468 (the Industry/University Cooperative
Research for Intelligent Maintenance Systems).
REFERENCES
Adler, D. Genetic Algorithms And Simulated Annealing:
A Marriage Proposal. Neural Networks, 1993., IEEE
International Conference, 1993 1993. 1104-1109
Vol.2.
Almuhtady, A., Lee, S. & Ni, J. 2012. Degradation-Based
Swapping Polcy With Application To System-Level
Manufacturing Utilization. ASME 2012 International
Manufacturing Science And Engineering Conference -
MSEC2012. Notre Dame, IN.
Benders, J. F. 1962. Partitioning Procedures For Solving
Mixed-Variables Programming Problems. Numerische
Mathematik, 4, 238-252.
Bertsimas, D. & Tsitsiklis, J. N. 1997. Introduction To
Linear Optimization, Athena Scientific.
Chvátal, V. 1983. Linear Programming, New York, W. H.
Freeman.
Duran, M. & Grossmann, I. 1987. An Outer-
Approximation Algorithm For A Class Of Mixed-
Integer Nonlinear Programs. Mathematical
Programming, 39, 337-337.
Fletcher, R. & Leyffer, S. 1994. Solving Mixed Integer
Nonlinear Programs By Outer Approximation.
Mathematical Programming, 66, 327-349.
Gao, C., Johnson, E. & Smith, B. 2009. Integrated Airline
Fleet And Crew Robust Planning. Transportation
Science, 43, 2-16.
Geoffrion, A. M. 1972. Generalized Benders
Decomposition. Journal Of Optimization Theory And
Applications, 10, 237-260.
Grossmann, I. E., S. A. Van Den Heever And I.
Harjunkoski, 2002. Discrete Optimization Methods
And Their Role In The Integration Of Planning And
Scheduling. AICHE Sympsium Series, 98, 150-168.
Gupta, O. K. & Ravindran, A. 1985. Branch And Bound
Experiments In Convex Nonlinear Integer
Programming. Management Science, 31, 1533-1546.
Hane, C. A., Barnhart, C., Johnson, E. L., Marsten, R. E.,
Nemhauser, G. L. & Sigismondi, G. 1995. The Fleet
Assignment Problem: Solving A Large-Scale Integer
Program. Mathematical Programming, 70, 211-232.
Holland, J. H. 1975. Adaptation In Natural And Artificial
Systems: An Introductory Analysis With Applications
To Biology, Control, And Artificial Intelligence,
Oxford, England: U Michigan Press.
Kocis, G. R. & Grossmann, I. E. 1987. Relaxation
Strategy For The Structural Optimization Of Process
Flow Sheets. Industrial & Engineering Chemistry
Research, 26, 1869-1880.
Lohatepanont, M. & Barnhart, C. 2004. Airline Schedule
Planning: Integrated Models And Algorithms For
Schedule Design And Fleet Assignment.
Transportation Science, 38, 19-32.
10000
15000
20000
25000
30000
1week 15days 20days 1month
Cost
∆
AMaintenance-optimalSwappingPolicy-ForaFleetofElectricorHybrid-electricVehicles
43

Metropolis, N., Rosenbluth, A., Rosenbluth, M., Teller, A.
& Teller, E. 1953. {E}Quation Of State Calculations
By Fast Computing Machines. Journal Of Chemical
Physics, 21.
Rexing, B., Barnhart, C., Kniker, T., Jarrah, A. &
Krishnamurthy, N. 2000. Airline Fleet Assignment
With Time Windows. Transportation Science, 34, 1-
20.
Robinson, J., Sinton, S. & Rahmat-Samii, Y. Particle
Swarm, Genetic Algorithm, And Their Hybrids:
Optimization Of A Profiled Corrugated Horn Antenna.
Antennas And Propagation Society International
Symposium, 2002. IEEE, 2002 2002. 314-317 Vol.1.
Rosenberger, J. M., Johnson, E. L. & Nemhauser, G. L.
2004. A Robust Fleet-Assignment Model With Hub
Isolation And Short Cycles. Transportation Science,
38, 357-368.
Schittkowski, K. 1982. The Nonlinear Programming
Method Of Wilson, Han, And Powell With An
Augmented Lagrangian Type Line Search Function.
Numerische Mathematik, 38, 115-127.
Smith, B. C. & Johnson, E. L. 2006. Robust Airline Fleet
Assignment: Imposing Station Purity Using Station
Decomposition. Transportation Science, 40, 497-516.
Talluri, K. T. 1996. Swapping Applications In A Daily
Airline Fleet Assignment. Transportation Science, 30,
237-248.
Viswanathan, J. & Grossmann, I. E. 1990. A Combined
Penalty Function And Outer-Approximation Method
For MINLP Optimization. Computers & Chemical
Engineering, 14, 769-782.
Westerlund, T. & Pettersson, F. 1995. An Extended
Cutting Plane Method For Solving Convex MINLP
Problems. Computers & Chemical Engineering, 19,
Supplement 1, 131-136.
Xia, W. & Wu, Z. 2005. An Effective Hybrid
Optimization Approach For Multi-Objective Flexible
Job-Shop Scheduling Problems. Computers &
Industrial Engineering, 48, 409-425.
ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems
44
