Measuring Musical Rhythm Similarity

Statistical Features versus Transformation Methods

J. F. Beltran, X. Liu, N. Mohanchandra and G. T. Toussaint

Faculty of Science, New York University Abu Dhabi, Abu Dhabi, U.A.E.

Keywords: Musical Rhythm, Similarity Measures, Transformations, Inter-Onset Interval Histograms, Mallows

Distance, Edit Distance, Statistical Features, Pattern Recognition, Music Information Retrieval, Mantel Test.

Abstract: Two approaches to measuring the similarity between symbolically notated musical rhythms are compared

with human judgments of perceived similarity. The first is the edit-distance, a popular transformation

method, applied to the rhythm sequences. The second works on the histograms of the inter-onset-intervals

(IOIs) of these rhythm sequences. Furthermore, two methods of dealing with the histograms are also

compared: the Mallows distance, and the employment of a group of standard statistical features. The results

provide further evidence from the aural domain, that transformation methods are superior to feature-based

methods for predicting human judgments of similarity. Furthermore, the results also support the hypothesis

that statistical features applied to the histograms of the rhythms are better than music-theoretical structural

features applied to the rhythms themselves.

1 INTRODUCTION

A fundamental problem in many scientific domains

is the measurement of similarity between a pair of

objects (Toussaint, 2013). There are two general

approaches to tackling this problem that have

received much attention in the literature: feature-

based methods and transformation-based

procedures. In feature-based methods a collection of

d features (measurements) is first calculated for each

object. Then the dissimilarity between two objects is

defined as the distance between their corresponding

feature vectors (Duda et al., 2000). The

transformation-based techniques on the other hand

measure similarity between two objects by the

minimum amount of work (suitably defined) that is

required to transform one object into the other.

Experimental evidence and consensus has been

accumulating, for at least a decade, which suggests

that in the visual domain, the transformation

methods appear to be superior to the feature-based

methods (Hahn et al., 2003). One such method

utilized in many pattern recognition applications is

the edit distance (also known as the Levenshtein

distance). Experiments have suggested that the edit

distance is a good predictor of human perceptual

judgments of rhythm similarity (Toussaint et al.,

2011); (Post and Toussaint, 2011). Furthermore, a

recent comparison of the edit distance with a

feature-based measure that employed a collection of

structural features common in music theory and

ethnomusicology for the purpose of classification,

has highlighted the superiority of the edit distance,

and has thus added support from the auditory

domain to the growing consensus of the advantages

of transformation methods observed in the visual

domain (Toussaint et al., 2012).

Here two approaches to measuring the similarity

between symbolically notated musical rhythms are

compared with each other and with human

judgments of perceived similarity: the feature-based

approach and the transformation method. In the

feature-based approach, unlike the music-theoretical

structural features used by Toussaint et al., (2012),

the features employed here are statistical features

computed from the Inter-Onset-Interval (IOI)

histograms of the rhythms, as was done with

acoustic input by Gouyon et al., (2004). For the

transformation approach we used two methods. The

first calculates the edit-distance, used frequently in

previous studies, directly on the rhythm sequences,

and the second calculates the Mallows distance from

the IOI-histograms (Levina and Bickel, 2001).

595

Beltran J., Liu X., Mohanchandra N. and Toussaint G. (2013).

Measuring Musical Rhythm Similarity - Statistical Features versus Transformation Methods.

In Proceedings of the 2nd International Conference on Pattern Recognition Applications and Methods, pages 595-598

DOI: 10.5220/0004325505950598

 SciTePress

2 TRANSFORMATION

METHODS

The Mallows distance (Levina and Bickel, 2001) is

closely related to the earth-mover's and

transportation distances and is quite complicated in a

general setting. In this study we use it in the context

of binary rhythm sequences all of which have the

same numbers of pulses and onsets. This implies that

the histograms of the IOIs have the same number of

bins. In this case the Mallows distance is simple and

may be computed efficiently in O(d) time, where d

is the cardinality of the two histograms being

compared.

The edit distance measures the least amount of

work needed to convert one rhythm to another by the

minimum number of basic operations (insertions,

deletions, and substitutions of symbols) that are

necessary to accomplish the task. An insertion of a

symbol into a sequence lengthens the sequence by

one symbol, a deletion shortens the sequence

accordingly, and a substitution exchanges one

symbol for another without altering its length.

3 STRUCTURAL FEATURES

Toussaint et al., (2012) compared the edit distance to

a feature-based method that used a group of 14

structural features that are frequently employed for

rhythm analysis and classification in music theory

and ethnomusicology. The data they used consisted

of the nine 8-pulse rhythms shown in Table 1. Thus

each rhythm was converted into a 14-dimensional

feature vector, and the dissimilarity between two

rhythms was measured by the 1st-order Minkowski

metric between their feature vectors. The listening

tests they performed with human subjects

demonstrated that the edit distance was successful at

predicting human judgments, whereas the feature-

based method fared quite poorly.

4 STATISTICAL FEATURES

The statistical features used here included the eight

features calculated from the IOI histograms that

were previously investigated by Gouyon et al.,

(2004) in the acoustic domain, and five additional

features calculated from the IOI values themselves.

The latter five features consisted of the shortest, the

longest, the range, the standard deviation, and the

Normalized Pairwise Variability index (nPVI). The

nPVI measures the directional change of the IOIs as

they occur in a sequence. Unlike the standard

deviation, which treats IOIs in isolation, the nPVI

measures the deviations between adjacent IOIs. It

was originally proposed for the analysis of

variability in speech rhythms using vocalic lengths.

More recently it has been explored as a general tool

in musical rhythm analysis (Toussaint, 2012).

5 THE RHYTHM DATA SETS

The experiments were done with two data sets that

had been used in previous studies. The first data set

consisted of six 16-pulse, 5-onset distinguished

Afro-Cuban timelines shown in box notation in

Table 1.

Table 1: The six 5-onset, 16-pulse rhythms used.

Rhythm Name Binary Box Notation

Shiko

× − − − × − × − − − × − × − − −

Son

× − − × − − × − − − × − × − − −

Soukous

× − − × − − × − − − × × − − − −

Rumba

× − − × − − − × − − × − × − − −

Bossa-Nova

× − − × − − × − − − × − − × − −

Gahu

× − − × − − × − − − × − − − × −

Table 2: The nine 8-pulse rhythms used.

Rhythm Name Binary Box Notation

2-3-3

× − × − − × − −

3-2-3

× − − × − × − −

Cinquillo-Variant

× − × × − × × ×

Cinquillo

× − × × − × × −

Conga

× − − × − − − −

Contradanza

× − × × × × × −

Habanera

× − − × × − × −

Tango-Congo

× − − × × − − −

Tresillo

× − − × − − × −

In this notation the symbols "×" and "−" stand for a

sounded unit-time pulse and a silent unit-time pulse,

respectively. These six rhythms had been used

previously to compare human judgments with the

edit distance (Toussaint et al., 2011). The second

data set consisted of nine Afro-Cuban rhythms of

eight pulses each, with onsets varying between two

and six, shown in box notation in Table 2, that had

been used in a former study to compare the edit

distance with the group of distinguished structural

features taken from music theory (Toussaint et al.,

2012).

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

596

6 RESULTS

To compare the various similarity measures with

each other and with human judgments, the

dissimilarity between every pair of rhythms in the

data was first calculated, obtaining a distance matrix.

Then a statistical procedure called the Mantel test

was used for calculating the correlation coefficients

between pairs of these distance matrices. The results

of the Mantel tests for the 16-pulse and 8-pulse

rhythms are listed in Tables 3 and 4, respectively,

where the statistically significant results are shown

in boldface type, and the asterisk indicates results

that were obtained in previous studies. Space

limitations do not permit the duplication here of the

description of the human listening tests performed

(for this see Toussaint et al., 2011).

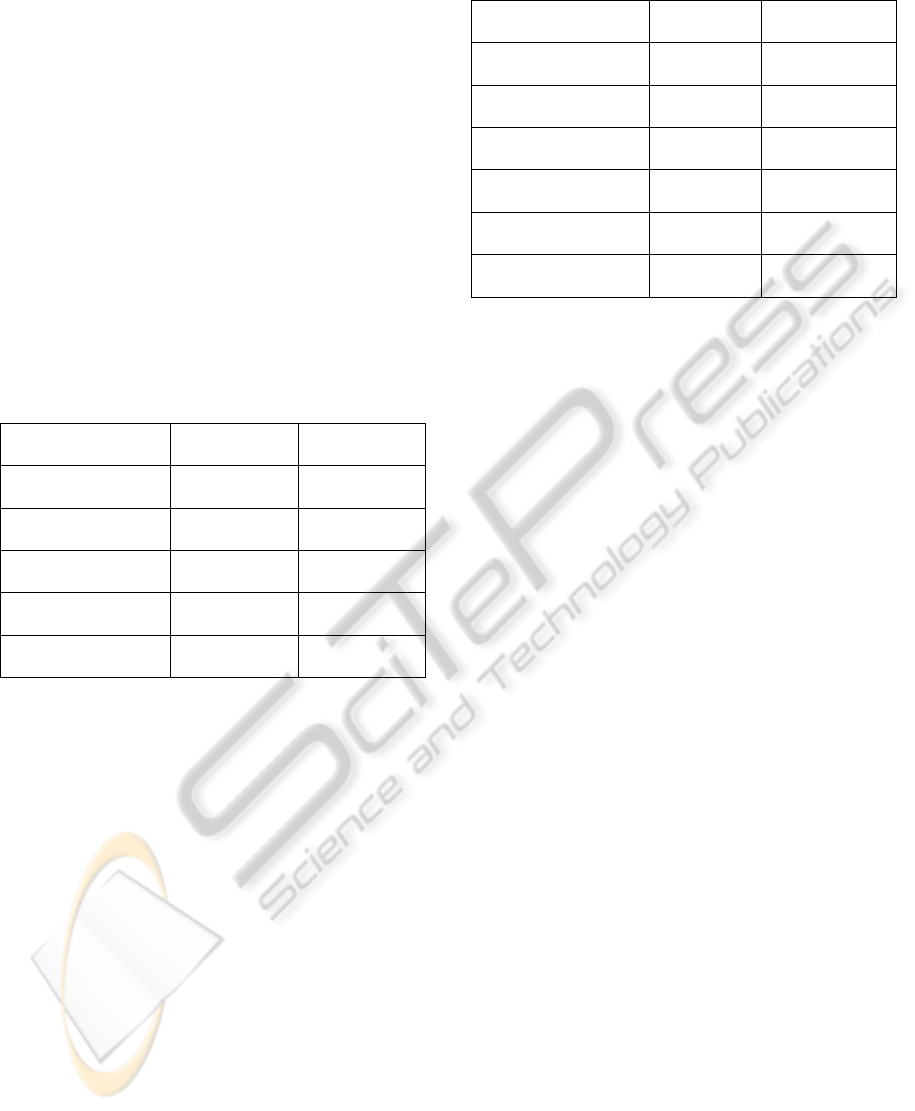
Table 3: Mantel test results for the 16-pulse rhythms.

Human

Judgment

Edit Distance

Statistical Features

r = -0.07

p = 0.47

r = -0.14

p = 0.28

Stat. Features and

nPVI

r = 0.02

p = 0.44

r = -0.09

p = 0.42

nPVI only

r = 0.24

p = 0.21

r = 0.07

p = 0.43

Normalized

Mallows Distance

r = 0.70

p = 0.02

r = 0.35

p = 0.2

Edit Distance*

r = 0.76

p = 0.02

−

Of all the experiments performed with the 16-pulse

rhythms, only the Mallows distance gave statistically

significant results, correlating highly with human

judgments (r = 0.70, p = 0.02). This is almost as

high as the previous result obtained with the edit

distance (r = 0.76, p = 0.02) calculated directly on

the rhythms themselves (Toussaint et al., 2011).

Note that in this corpus all the rhythms have the

same number of onsets, and therefore corpus

normalization is equivalent to pairwise

normalization.

By contrast with the 16-pulse rhythms, all the

experiments with the 8-pulse rhythms, yielded mild

but statistically significant correlations with human

judgments. The nPVI, a successful measure of

rhythm complexity (Toussaint, 2012), gave the

lowest correlation (r = 0.25, p = 0.04) when used in

isolation, and all the other models yielded

correlation coefficients ranging between 0.48 and

0.43. This represents a significant drop from the

previously obtained result with the edit distance (r =

0.59, p = 0.0002) when calculated directly on the

Table 4: Mantel test results for the 8-pulse rhythms.

Human

Judgment

Edit Distance

Statistical Features

r = 0.43

p = 0.006

r = 0.57

p = 0.003

Stat. Features and

nPVI

r = 0.46

p = 0.003

r = 0.57

p = 0.003

nPVI only

r = 0.25

p = 0.04

r = -0.05

p = 0.44

Corpus-Normalized

Gen. Mallows Dist.

r = 0.45

p = 0.003

r = 0.41

p = 0.03

Pairwise-Normalized

Gen. Mallows Dist.

r = 0.48

p = 0.001

r = 0.21

p = 0.1

Edit Distance*

r = 0.59

p = 0.0002

−

rhythm sequences (Toussaint et al., 2012). In this

corpus the number of onsets in the rhythms varies

considerably, and therefore the results with the

corpus and pairwise normalizations differ a little.

Surprisingly, the statistical features calculated from

the IOI histograms correlate quite highly with the

edit distance.

7 CONCLUSIONS

One of the main conclusions we can draw from this

study is that the statistical features calculated from

the inter-onset interval histograms, used by Gouyon

et al. (2004) in the context of music information

retrieval, are much better than the music-theoretical

structural features investigated previously by

Toussaint et al., 2012), for predicting human

judgments of rhythm similarity. The Mallows

distance computed from the IOI histograms gave the

best results obtained here, providing further

evidence to support the hypothesis that

transformation methods are superior to feature-based

methods as tools for predicting human judgments of

similarity.

REFERENCES

Duda, R. O., Hart, P. E., & Stork, D. G., 2000. Pattern

Classification, Wiley-Interscience, 2

Edition.

Gouyon, F., Dixon, S., Pampalk, E., & Widmer, G., 2004.

Evaluating rhythmic descriptors for musical genre

classiﬁcation. Proc. 25th Int. AES Conference.

Hahn, U., Chater, N., & L. B. Richardson, L. B., 2003.

Similarity as transformation. Cognition, 87, 1-32.

Levina, E. & Bickel, P. (2001). The earth mover’s distance

is the Mallows distance: Some insights from statistics.

Proceedings Eighth IEEE International Conference on

MeasuringMusicalRhythmSimilarity-StatisticalFeaturesversusTransformationMethods

597

Computer Vision, Vancouver, Canada, 2, 251-256.

Post, O. & Toussaint, G. T. 2011. The edit distance as a

measure of perceived rhythmic similarity. Empirical

Musicology Review, 6, 3, 164-179.

Toussaint, G. T., 2013. The Geometry of Musical Rhythm.

Chapman-Hall/CRC Press.

Toussaint, G. T., 2012. The pairwise variability index as a

tool in musical rhythm analysis. Proc. 12th Int. Conf.

Music Perception and Cognition (ICMPC),

Thessaloniki, Greece, July 23-28, 1001-1008.

Toussaint, G. T., Mathews, L., Campbell, M., & Brown,

N., 2012. Measuring musical rhythm similarity:

Transformation versus feature-based methods, (in

preparation).

Toussaint, G. T., Campbell, M., & Brown, N., 2011.

Computational models of symbolic rhythm similarity:

Correlation with human judgments. Analytical

Approaches to World Music, 1, 2.

ICPRAM2013-InternationalConferenceonPatternRecognitionApplicationsandMethods

598