Segmenting and Selecting Cross-sale Prospects using Dynamic Pricing

Fredrik Thuring

, Jens Perch Nielsen

, Montserrat Guill´en

and Catalina Bolanc´e

Faculty of Actuarial Science and Insurance, Cass Business School, 106 Bunhill Row, London, EC1Y 8TZ, U.K.

Riskcenter-IREA, Dept. Econometrics, University of Barcelona, Diagonal 690, 08034 Barcelona, Spain

Keywords:

Cross-Sales, Call Center, Dynamic Pricing, Price Elasticity of Demand, Closed form Expressions, Multivari-

ate B¨uhlmann-Straub Credibility, Financial Services, Insurance Industry.

Abstract:

In this paper we consider segmentation of a company’s customer data base with respect to the future expected

proﬁt, emerging from not yet sold products. We consider a situation where the company is interested in

contacting a subset of the customers in the data base to offer additional products. The price at which the

products are offered may vary and by utilizing an estimate of the price elasticity of demand, we are able to ﬁnd

closed a form expression of the optimal price as well as the corresponding expected proﬁt, for each customer

prospect. We implement the methodology and test it using real data from a major Scandinavian insurance

company. We underline that a closed form expression of the optimal price is seldom found in the dynamic

pricing literature, suggesting that our pricing formula would be of interest to a broad audience of economists,

econometricians, pricing managers and actuaries.

1 INTRODUCTION

This paper addresses the challenge of setting an opti-

mal price and segmenting a customer data base with

respect to the proﬁt that is expected to emerge from

a cross-sale attempt. Of particular interest is the ﬁ-

nancial services industry where companies have sig-

niﬁcant data bases and a traditional long relationship

with each customer, once they purchase their prod-

ucts. Normally, the cross sale challenge is associated

with using the company’s speciﬁc knowledge of e.g.

the probability of a cross sale, the cost of a cross sale

attempt, the average discounted future proﬁt and the

uncertainty of the proﬁt of the entire cross sale at-

tempt for that individual. In this paper we propose an

extension to this approach by introducing an estimate

of the price elasticity of demand and deriving an ex-

pression for the optimal price at which the additional

product should be sold, in order to maximise proﬁt to

the company.

Proﬁt emerging from contacting subsets of cus-

tomers has been considered by e.g. Bult and Wans-

beek (1995), Venkatesan and Kumar (2004), G¨on¨ul

and Hofstede (2006) and Kaishev et al. (2012). In

Bult and Wansbeek (1995), the optimal selection is

based on the customer response (sale or no sale) to a

direct marketing offer of books, periodicals and music

to households by a retailer in the Netherlands. Given

sale, it is assumed that the marginal, i.e. per customer,

return (proﬁt) is deterministic. Customer selection

based on customer life time value is considered in

Venkatesan and Kumar (2004) where the model uti-

lizes classical regression techniques. G¨on¨ul and Hof-

stede (2006)takes the approach further by introducing

optimisation objectives such as proﬁt maximisation,

customer retention and utility maximisation. They ap-

ply their methodology to the problem of setting opti-

mal sales catalogue mailing strategies. In Kaishev et

al. (2012) a model is presented for the customer spe-

ciﬁc proﬁt given a cross-sale approach. The proﬁt to

the company is generated by the stochastic income, at

point of sale, minus the cost of contacting a speciﬁc

customer minus the stochastic cost generated by the

customer as an effect of his/her actions. The model

is primarily directed towards applications in the in-

surance and banking sector where customers can be

associated with either claims or loan defaults, affect-

ing the company’s proﬁt. None of the studies con-

sider changing the price at which products are offered

in order to boost revenue and proﬁt. In this paper we

argue that by introducing elasticity of demand and dy-

namic pricing into customer segmentation studies, as

described above, the customer selections would im-

prove further and increase the proﬁt to the company.

The literature on traditional cross-sale models is vast

and we refer the interested reader to papers by Ka-

301

Thuring F., Perch Nielsen J., Guillén M. and Bolancé C..

Segmenting and Selecting Cross-sale Prospects using Dynamic Pricing.

DOI: 10.5220/0004336401030108

In Proceedings of the 2nd International Conference on Operations Research and Enterprise Systems (ICORES-2013), pages 103-108

ISBN: 978-989-8565-40-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

makura et al. (1991), Knott et al. (2002), Kamakura

et al. (2003), Kamakura et al. (2004), Li et al. (2005),

Kamakura (2007), and Li et al. (2010).

We consider the ﬁnancial service industry primar-

ily because of the large customer data bases normally

available as well as the speciﬁc structure of the of-

fered products. Financial services offered by banks

and insurance companies, such as mortgage contracts

and other types of loans, household, car and motor-

cycle insurance policies, and other types of personal

lines insurance products, differ in several ways from

other conventional retail products and services which

other companies offer. There is a policy duration

speciﬁed at the date of sale of a ﬁnancial product

and also the cost associated with a speciﬁc customer

is stochastic and becomes known to the organization

at some random time after the sales date. For ex-

ample, the cost generated by an insurance policy is

mainly determined by the claim amount which de-

pends on the occurrence and severity of the related

insured event. In a mortgage setting, a holder of a

mortgage contract may default on his/her loan repay-

ment at some random moment within the duration of

the contract, which may lead to a loss for the lending

bank or its insurance company, of unknown (random)

size.

To be able to introduce elasticity of demand and

dynamic pricing into a cross-sale model, we consider

the model from Kaishev et al. (2012). This model in-

volves three random quantities, a binary random vari-

able, modelling the event of cross-selling, a random

variable modelling the price of the offered product

and another random variable, modelling the cost as-

sociated with a speciﬁc customer for the cross-sale

product. We generalise the model by introducing a

relation between the probability of a successful cross-

sale and a price change variable c

> −1 for customer

i and product k. Also the offered price Π

is related

to c

and a tariff price Π

0ik

as Π

= (1+ c

)Π

0ik

With these introductions to the model of Kaishev et

al. (2012) we are able to derive a closed form expres-

sion of the customer speciﬁc optimal price change c

∗

which maximises expected proﬁt from each customer.

2 A MODEL FOR CROSS-SALE

PROFIT UNDER THE

INFLUENCE OF PRICE

ELASTICITY

We consider a company, offering K different prod-

ucts, and a set of i = 1, . . . , I customers for which the

stochastic proﬁt H

, for a product k ∈ {1, . . . , K}, is

of interest. We assume that all I customers are in pos-

session of at least one product k

′

∈ {1, . . . , k − 1, k +

1, . . . , K}, but not product k, wherefore the proﬁt, with

respect to product k, is of stochastic nature. The com-

pany may contact the customers to cross-sell product

k, by which the customer response (purchase/no pur-

chase) is modeled by a Bernoulli random variable A

with success probability p

. The company has inﬂu-

ence over the offered price Π

, to a speciﬁc customer

i, by adjusting the tariff price Π

0ik

with a price change

parameter c

> −1 as Π

= (1+ c

)Π

0ik

. The tariff

price Π

0ik

is a stochastic variable since it may be in-

ﬂuenced by customer decisions such as add-ons and

other customisation not known to the company prior

to the cross-sale contact. We assume that the success

probability p

is dependent of the price change pa-

rameter c

, a cross-sale probability p

0ik

and a price

elasticity e

> 0 as p

0ik

(1+c

)

. It should be noted

that p

decreases as the price change parameter c

increases and that p

= p

0ik

for c

= 0 (i.e. no price

change). The cross-sale product k is associated with a

stochastic cost S

as well as a deterministic cost ω

for performing the cross-sale contact to the customer.

We assume that a customer’s response to a cross-sale

contact A

is not related to the tariff price Π

0ik

or the

stochastic cost S

, i.e. A

is independent of Π

0ik

and

. Inspired by the model of Kaishev et al. (2012),

we propose an extended model taking the price elas-

ticity e

into account as the following.

= l

}

(Π

− S

) − ω

(1)

}

(

1, p

0, 1− p

0ik

(1+c

)

= (1+ c

)Π

0ik

The model of Kaishev et al. (2012) is a special

case of the proposed model with c

= 0. We denote

by µ

= E [H

] the expectation of the stochastic vari-

able H

for which we have the expression

= E [H

] =

0ik

(1+c

)

((1+ c

)E (Π

0ik

) − E (S

)) − ω

(2)

where we have used that A

is independent of Π

0ik

and S

3 OPTIMISATION OF THE

EXPECTED PROFIT

We are interested in ﬁnding the value of the price

change parameter c

for which the expected proﬁt (2)

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

302

is maximised. We present the following proposition.

Proposition.

Proposition. The price change c

∗

which maximises

in (2) is the following

∗

E (S

E (Π

0ik

)(e

− 1)

− 1. (3)

Proof.

Proof. We can rewrite (2) as follows

= p

0ik

E (Π

0ik

)(1+ c

)

(1−e

)

−

0ik

E (S

)(1+ c

)

−e

− ω

Differentiating with respect to c

gives

dµ

= p

0ik

E (Π

0ik

)(1− e

)(1+ c

)

−e

−

0ik

E (S

)(−e

)(1+ c

)

−e

−1

= p

0ik



E(Π

0ik

)(1−e

)

(1+c

)

E(S

(1+c

)



and by equating to zero (noting that p

0ik

> 0) we get

E(Π

0ik

)(1−e

)

(1+c

)

E(S

(1+c

)

= 0.

The above can be rewritten as

(1+ c

)

−e

(E (Π

0ik

)(1− e

)(1+ c

) + E (S

) = 0.

Noting that c

> −1 we get

E (Π

0ik

)(1− e

)(1+ c

) + E (S

= 0

which is solved by

E(S

E(Π

0ik

)(e

−1)

− 1.



From (3) it should be noted that e

> 1 for the optimal

price change c

∗

to be feasible. In economic terms,

this means that the demand for the good need to be

elastic or relatively elastic. The maximum expected

proﬁt µ



∗



for customer i is received by insertion

of (3) into (2) and after some algebraic manipulations

it yields

∗

) = p

0ik



E (Π

0ik

)





− 1

E (S

)



−1

− ω

(4)

With the expression for the optimal price change (3)

and the corresponding proﬁt (4) the company is able

to assess whether or not a certain customer should

be contacted and offered the product k, at the price



1+ c

∗



0ik

. The possibility of µ



∗



< 0

should be noted, i.e. even at the optimal price change

some customers are expected to contribute negatively

to the proﬁt of the company and should therefore not

be contacted.

4 VARIABLE SPECIFICATION

AND PARAMETER

ESTIMATION

For speciﬁcation of the variables Π

0ik

, S

and ω

0ik

the model (2) we follow the approach of Kaishev et

al. (2012) and consider the insurance business where

problems regarding which customers to cross-sell to,

at which price, are common. For the expected value of

the stochastic variable describing the tariff price Π

0ik

we use the mean value from a collateral data set of the

company as E (Π

0ik

) =

For the variable S

we follow standard actuarial

convention and identify it as the aggregate claims cost

∑

t=1

ikt

, where N

describes the stochastic num-

ber of insurance claims (for customer i) and X

de-

scribes the corresponding monetary size of each of

these claims. Additionally, we let each customer i be

associated with a latent risk variable Θ

modelling

unobserved characteristics related to the risk of that

customer, for which θ

is its realisation. The expec-

tation of N

, conditioned on the latent random risk

variable Θ

, is E [N

| Θ

= θ

] =

and X

has

expectation E [X

] = ¯x

is sometimes called the

a priori expected number of claims. Both

and ¯x

denote the mean value for which collateral data from

the company is needed in the estimation. By assum-

ing independence between N

and X

the expectation

of S

(conditioned on Θ

) becomes

E [S

| Θ

= θ

] = E [N

| Θ

= θ

]E [X

] =

¯x

(5)

We use multivariate credibility theory to estimate

and speciﬁcally the estimator presented in Thur-

ing (2012). This estimator produces an estimate of

, for the cross-sale product k for which no customer

speciﬁc data is available, using available information

with respect to another product k

′

. We assume that

customer speciﬁc data is available for the a priori ex-

pected number of claims λ

′

and observed number of

claims n

′

, with n

′

being a realisation of N

′

, for all

I customers.

= θ

′

+ σ

′



′

− θ

′



(6)

In order to be able to evaluate (6), estimates of θ

′

, τ

′

, σ

′

and θ

′

need to be obtained from collat-

eral data of the company, see e.g. B¨uhlmann & Gisler

(2005) p. 185-186. For further details, see also En-

glund et al. (2009) and Thuring et al. (2012).

For the cost of a cross-sale contact ω

we con-

sider the speciﬁc case of each cross-sale contact be-

ing equally costly for the company and therefore use

SegmentingandSelectingCross-saleProspectsusingDynamicPricing

303

as estimator ω

= ω

, where ω

is estimated with ap-

propriate data of the company.

The cross-sale probability p

0ik

is estimated using

a regression model p

0ik

= f

p,k



p,ik



, where f

p,k

an appropriate regression function, estimated based

on collateral data from the insurance company and

p,ik

is a set of customer speciﬁc antecedents of the

contacted customer, see related studies of Knott et al.

(2002) and Li et al. (2005) where suggestions for f

p,k

are given.

For the price elasticity e

we consider the deﬁni-

tion of price elasticity as the logarithm of the percent-

age change in demand over the logarithm of the per-

centage change in price. Furthermore we assume that

we have collateral data available where the success of

a large number of cross-sale contacts has been regis-

tered and that a random number of the contacts have

been associated with a price change c

. The price

change have been introduced to measure its effect on

sales success of the cross-sale contacts. To be able to

estimate the price elasticity we denote by ¯p

the esti-

mated probability of cross-sale success, for contacts

associated with no price change. Furthermore, we

denote by ¯p

the estimated probability of cross-sale

success, for contacts associated with a price change

of c

. According to the deﬁnition of price elasticity

we have



¯p



ln(1+ c

)

. (7)

5 REAL DATA STUDY

We have available the data base of a major Scandi-

navian insurance company within non-life personal

lines insurance (home, building, car, boat, etc.). To

be able to estimate the necessary parameters for (3)

and (4) we need data from different sources within

company’s data base. The average values of the tariff

price

is easily calculated from the data of all ex-

isting customer in possession of product k. Also the

average a priori expected number of claims

and the

average claim severity ¯x

is available by considering

all claims historically reported to the company in re-

lation to the risk exposure (total number of years for

all customers).

In order to be able to evaluate (6), estimates of

, τ

′

, τ

′

, σ

′

and θ

′

need to be obtained from

a collateral data set consisting of present customers

in possession of both product k and k

′

. The estimates

are found in Table 1. These estimates are needed to

estimate the customers speciﬁc risk proﬁle

The constant cost of a cross-sale contact ω

estimated by analysing data on stafﬁng cost and of-

Table 1: Estimates of the model parameters for estimating

the customer speciﬁc risk proﬁle

1 1.755 0.081 0.130 1.12

2 1.349 0.130 0.211 0.91

ﬁce rent, collected at the call center of the company.

The regression function f

p,k



p,ik



, for the cross-sale

probability p

0ik

, is based on data from past cross-sale

attempts, details on variable selection and parame-

ter estimates cannot be disclosed due to conﬁdential-

ity agreements between the authors and the company.

The estimate of the price elasticity e

is received from

a unique data set of insurance quotes subject to a ran-

dom price change in order to measure its effect on the

realisation of random variable A

(sale/ no sale).

Our validation data set, for implementation of

the formulas (3) and (4), is a data set consisting of

I = 4463 insurance customers who were targeted for

a cross-sale campaign (in the following referred to as

the campaign data set). These speciﬁc customers were

approached, via telephone, and were, at the time of

contact, in possession of a household insurance cov-

erage (in the following referred to as product k

′

= 1).

The aim of the telephone call was to cross-sell a car

insurance coverage (in the following referred to as

product k = 2). Not every customer accepted the cross-sale

offer, of the 4463 contacted household policyholders, 177

purchased the car insurance coverage, i.e.

∑

i=1

}

= 177.

Our aim with this data is to examine the expected

proﬁt from each of the customers, with respect to

product k = 2, and how the proﬁt is related to dif-

ferent values of the price change c

. Of particular

interest is the optimal price change c

∗

and its corre-

sponding proﬁt µ

∗

), according to (3) and (4), in

comparison to c

= 0 which corresponds to the model

of Kaishev et al. (2012). Table 2 presents summary

statistics of all the necessary parameters from both the

collateral data sets and the campaign data set.

We apply (3) and (4) to all the records of the

campaign data set and present the results through his-

tograms, see ﬁgure 1. In ﬁgure 1 we have also in-

cluded a graph showing cumulative sums of the ex-

pected proﬁt

∑

i=1

ˆµ

(with no price change, c

= 0) and

compared this to cumulative sums

∑

i=1

ˆµ

∗

(with opti-

mal price change, c

∗

), for l = 1, . . . , 4463. The

campaign data set is sorted by decreasing proﬁt, ˆµ

and ˆµ

∗

respectively, prior to cumulative summation.

By this approach the curves show the total expected

proﬁt from an increasing subset of customers and the

optimal number of customers to contact is where the

curve has its maximum. For the expected proﬁt as-

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

304

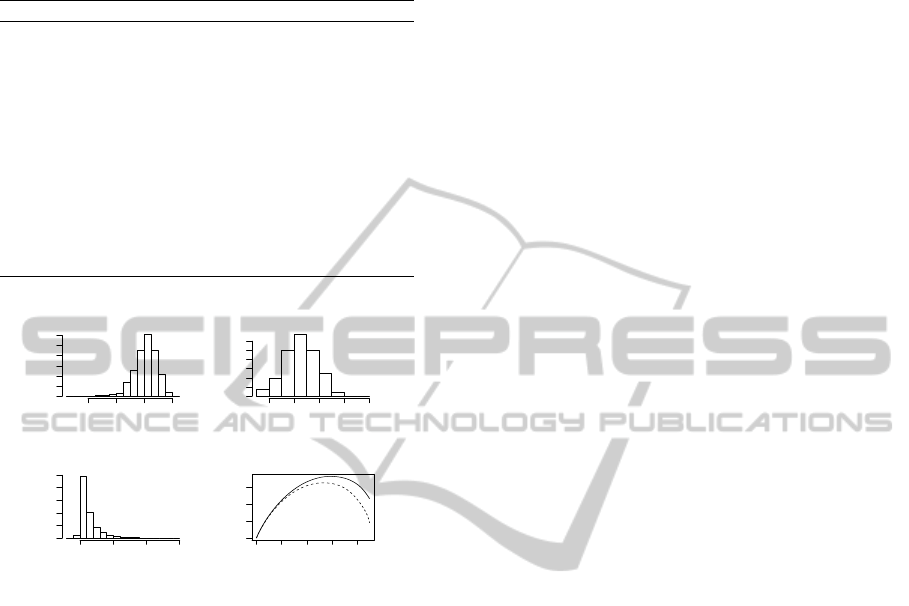
Table 2: Descriptive statistics of the campaign data set, note

that k

′

= 1 represents household insurance coverage and that

k = 2 represents car insurance coverage.

Constant Min Max Mean

- 0.0083 3.92 0.64

1.12 - - -

}

- 0 1 0.040

ˆp

- 0.0040 0.13 0.069

- 0.71 2.05 0.95

0.91 - - -

0.375 - - -

ˆm

($) 2, 025 - - -

($) 949 - - -

($) 15 - - -

ˆe

3 - - -

Histogram of µ

(0)

Frequency

−40 −20 0 20

0 400 800 1200

Histogram of µ

)

Frequency

−10 0 10 20 30

0 400 800

Histogram of c

Frequency

0.0 0.5 1.0 1.5

0 1000 2000

0 1000 3000

0 5000 15000

Number of contacts

Expected profit, µ

Figure 1: Top left is a histogram over expected proﬁts asso-

ciated with no price change µ

(0), top right is a histogram

over expected optimal proﬁts µ



∗



, bottom left is a his-

togram of the optimal price changes c

∗

and the bottom right

graph shows cumulative sorted sums

∑

i=1

ˆµ

(dotted) and cu-

mulative sorted sums

∑

i=1

ˆµ

∗

(solid).

sociated with c

= 0 this is 2647, while applying the

optimal price change to each customer c

∗

, results in

2934 customers having a positiveexpected proﬁt. The

resulting total expected proﬁt from these 2647 and

2934 customers is $16, 416 and $18, 338, an increase

of almost 12%. The average value of price changes is

calculated to 0.13, i.e. the optimal prices offered to

the cross-sale customers is 13% above the tariff price.

6 CONCLUSIONS

In this paper, we have derived a closed form expres-

sion for the customer speciﬁc optimal price change

and the corresponding optimal proﬁt. The staring

point is the model of Kaishev et al. (2012) which has

been generalised towards a situation where the prob-

ability of success, of a cross-sale attempt, is depen-

dent of the price at which the product is offered. The

new approach is tested on data from a major Scan-

dinavia insurance company where the target group of

customers (associated with positive expected proﬁt)

increase as optimal price changes are applied. The re-

sulting formula for optimal price change is not only of

interest to researcher and practitioners of cross-selling

but could be applied in a far broader context of pricing

in general.

REFERENCES

Bult, J. R. and Wansbeek, T., 1995. Optimal selection for

direct mail, Marketing Science, 14(4), 378-394.

B¨uhlmann, H. and Gisler, A., 2005. A Course in Credi-

bility Theory and its Applications (Berlin, Germany:

Springer Verlag).

Englund, M., Gustafsson, J., Nielsen, J. P. and Thuring, F.,

2009. Multidimensional Credibility with Time Effects

- An Application to Commercial Business Lines, The

Journal of Risk and Insurance, 76(2), 443-453.

G¨on¨ul, F. F. and Hofstede, F.T., 2006. How to compute

optimal catalog mailing decisions, Marketing Science,

25(1), 65-74.

Kaishev, V. K., Nielsen, J. P., Thuring, F. 2012. Opti-

mal customer selection for cross-selling of ﬁnancial

services products, Expert Systems with Applications,

forthcoming.

Kamakura, W.A., 2007. Cross-Selling: Offering the Right

Product to the Right Customer at the Right Time in

Lehzan Aksoy, Timothy Keiningham and David Be-

jou (Eds.) Proﬁt Maximization through Customer Re-

lationship Marketing , Haworth Press.

Kamakura, W. A., Kossar, B. and Wedel, M., 2004. ”Iden-

tifying innovators for the cross-selling of new prod-

ucts,” Management Science, 50, 1120-1133

Kamakura, W. A., Wedel, M., de Rosa, F. and Mazzon, J.

A., 2003. Cross-selling through database marketing: a

mixed data factor analyzer for data augmentation and

prediction, International Journal of Research in Mar-

keting, 20(1), 45-65.

Kamakura, W. A., Ramaswami, S. and Srivastava R., 1991.

Applying latent trait analysis in the evaluation of

prospects for cross-selling of ﬁnancial services, Inter-

national Journal of Research in Marketing, 8, 329-

349.

Knott A., Hayes, A. and Neslin, S. A., 2002. Next-product-

to-buy models for cross-selling applications, Journal

of Interactive Marketing, 16(3), 59-75.

Li, S., Sun, B. and Montgomery, A. L. 2010. Cross-Selling

the Right Product to the Right Customer at the Right

Time, Journal of Marketing Research, 48(4), 683-700.

Li, S., Sun, B. and Wilcox, R. T., 2005. Cross-selling se-

quentially ordered products: an application to con-

sumer banking services, Journal of Marketing Re-

search, 42, 233-239.

SegmentingandSelectingCross-saleProspectsusingDynamicPricing

305

Thuring, F., 2012. A credibility method for proﬁtable cross-

selling of insurance products, Annals of Actuarial Sci-

ence, 6(1).

Venkatesan, R. and Kumar, V., 2004. A customer life-

time value framework for customer selection and re-

sources allocation strategy, Journal of Marketing, 68,

106-125.

ICORES2013-InternationalConferenceonOperationsResearchandEnterpriseSystems

306