Knowledge Controlled Mathematical Coaching
Strategies and Results of a Personalized Blended Learning Approach
Michael Schäfer
Computer Science Institute, University of Applied Sciences Ruhr West, Tannenstraße 43, Bottrop, Germany
Keywords: Mathematical Coaching, Bridging Courses, Personalization, Blended Learning.
Abstract: The mathematical competence of first year students is an important success factor at least for technical
studies. As a significant percentage of students do not have sufficient mathematical skills, universities often
utilise blended learning courses to increase these skills prior to the start of studies. Due to the diversity of
students and their educational backgrounds, individual strategies are needed to achieve the necessary
competence for successfully managing their studies. This paper describes our approach at the University of
Applied Sciences Ruhr West, where we are using personalized blended learning concepts based on the
measurement of individual mathematical competences at the beginning of a coaching process. This is used
to gain a better matching between the individual learner level and the adapted learning concepts. We
combine individual presence learning groups and a personalized e-learning environment. This environment
is adapted based on mathematical skills of each student. It uses individual learning advices, short-term
optical feedback and up to date e-learning material in a Moodle-based LMS (learning management system).
The coaching concept is approved by the results of summative and formative evaluations.
1 INTRODUCTION
In recent years, university professors in technical
studies report decreasing mathematical skills and an
increasing diversity of their educational classes.
Since 2002 the mathematical skills at the
Universities of Applied Science in North Rhine
Westphalia have been tested. The mathematical
competence has been evaluated in a standardized
mathematical test carried out on the first day of their
university education since then.
Ten basic mathematical subjects (e.g. solving
equations, quadratics, powers and logarithms, linear
equation) have to be solved.
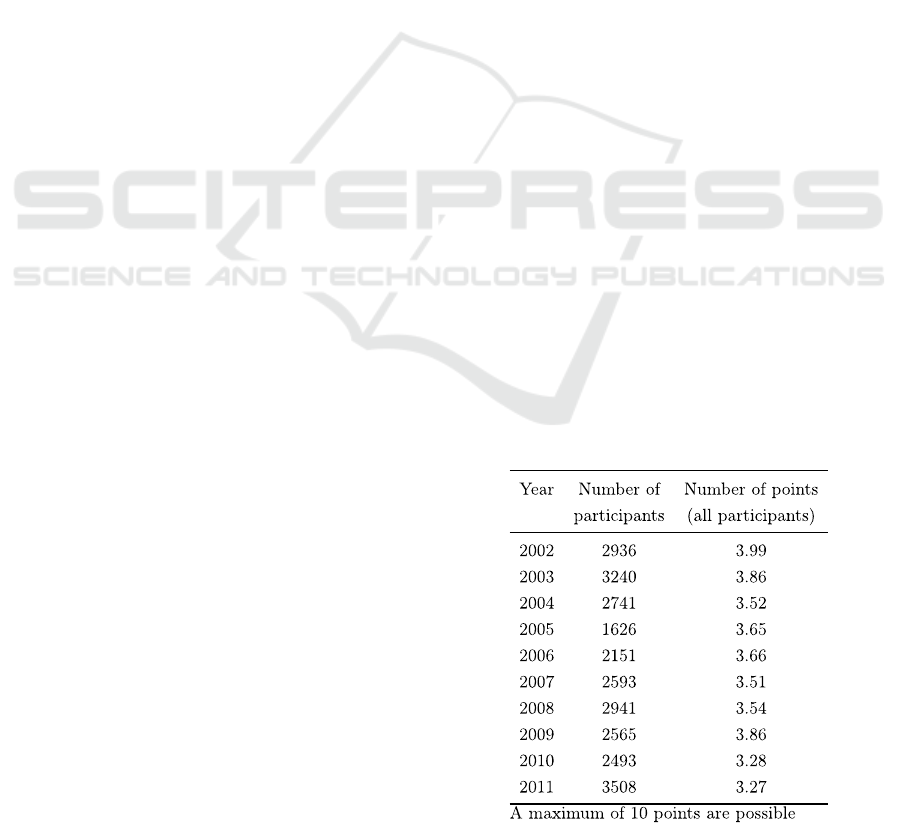
The average value of solved questions is shown
in column three of Table 1 (Knospe, 2012).
The already disappointing results of 2002 are
continuously getting poorer.
The approach described here utilizes an
individual adapted mathematical coaching for each
student in order to improve and equalise the
qualifications of all students before the beginning of
their university education.
Table 1: Results of math-examination before the start of
studies.
This paper starts with a section about related
work and continues with a description of the
architectural approach and detailed information
about the implementation, shows results of the
evaluation of the system described and concludes
with an outlook on planned future work.
484
Schäfer M..
Knowledge Controlled Mathematical Coaching - Strategies and Results of a Personalized Blended Learning Approach.
DOI: 10.5220/0004343204840488
In Proceedings of the 5th International Conference on Computer Supported Education (CSEDU-2013), pages 484-488
ISBN: 978-989-8565-53-2
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK
In a blended scenario, our approach combines an
online learning course and presence courses that are
adjusted to the results of a mathematical test.
(Schäfer et al., 2012).
The online course is developed due to the
approach of the ARCS-Modell of motivational
design by John Keller (Keller, 2010). It uses
different elements to gain and keep the attention of
the students and to increase the satisfaction, as these
are main factors of learner motivation.
We use several concepts of personalized
feedback to keep motivation and support the
learning outcome. This is similar to concepts of Saul
and Wuttke (Saul and Wuttke, 2011). Regarding the
results of Jarvis and de Freitas (Jarvis and de Freitas,
2009) on the effects of in-game feedback to the
learning transfer improvement, we are using similar
feedback mechanisms. In a first pilot study we
enriched our interface with a humanoid avatar to
improve learning effects as evaluated by Ayad
(Ayad, 2010). The learning design considers aspects
of diversity as shown by Bhattacharya and Hartnett
(Bhattacharya and Hartnett, 2008). To improve the
quality of the coaching concept it is embedded in a
quality improving process based on a modification
of the PDCA cycle (Deming, 1986).
3 ARCHITECTURAL APPROACH
The central idea of our approach is to improve the
matching between the individual knowledge of each
student and our online and offline teaching
strategies. Therefore, each student does a
mathematical test with 48 items out of fifteen topics
as shown in Table 2.
Table 2: Topics of the mathematical test.
The results are stored in a database and used to adapt
the online and presence courses. Further information
is presented in (Schäfer
et al., 2012).
In order to design the presence courses three
clusters of different ability levels are built. Students
with low abilities have courses with a duration of
three weeks starting in small groups with less than
ten participants. Medium-level student courses will
take two weeks while high-level student courses will
last only one week. An overview is presented in
Table 3.
Table 3: Presence learning group arrangement.
New students have to complete the courses
weekly to prevent a separation in different learning
groups corresponding to the ability levels. Students
with low-level abilities are starting in small groups
of 10 participants. After one week students with
medium abilities join these groups up to a maximum
of 25 participants. They are starting again with the
same mathematical subjects, but quicker.
One week later, students with high-level abilities
complete the courses up to 35 participants and the
whole course starts again with the same subjects but
even quicker.
The advantage of this is that the students with
lower abilities had the possibility of repeating the
same subjects several times. The learning velocity of
students with higher abilities is adequately taken into
account. We prevent a separation of students due to
their different skills in the beginning because all
students should recognise an equalized state of
knowledge of the other participants in their course.
The online-learning course starts prior to the
presence courses and it can be attended additionally.
The course is adapted for every student. The results
of the mathematical test are taken into account for a
dynamic generation of personal feedback and for
giving learning advice. The feedback is given with
textual and graphic analysis, symbolic and textual
learning advice. Due to the motivational design by
John Keller, screencasts are used to get attention and
simple mathematical tests with optical feedback are
used to keep attention, to show the learning
enhancement and to support confidence and
satisfaction. Like in serious games the personal aim
is to get as much positive optical feedback as
possible.
The adapted blended learning design as shown
KnowledgeControlledMathematicalCoaching-StrategiesandResultsofaPersonalizedBlendedLearningApproach
485
above is summative and formative evaluated. Due
to this the learning outcome proven and structured
feedback is available to optimise the whole coaching
process.
4 IMPLEMENTATION
The mathematical coaching was developed in the
year 2010 and it was used with 335 students in the
year 2011. After a formative evaluation with the
result of an overall good feedback but a less good
acceptance of the online learning course (Schäfer
et
al.,
2012), the motivational elements were
enhanced. In the year 2012, more than 600 students
took part.
The mathematical test of each student was done
as paper and pencil test. Here, an anonymous
number and the email-address were collected to be
able to send necessary information about the
organisation of the presence and online courses. The
results were stored in an SQL-database being part of
the learning management system (LMS). Moodle
(Moodle Development Team, 2012)
was used as
LMS.
Twenty teachers in three locations have done the
presence courses after a professor of the university
instructed them. Clustering students through
competence and study path did the matching. A
homogenies cluster with a teacher of the same
background/similar degree was built.
An individual mail with the account data to the
LMS, the time and place of the best matching
mathematical courses was generated and distributed.
The online mathematical course combines an all-
embracing amount of learning material with a
pedagogical and motivational concept to improve
the usage of this material and the learning outcome.
The LMS-design is based on the university corporate
design and enhanced with many graphical and
interactive elements. The front page is shown in
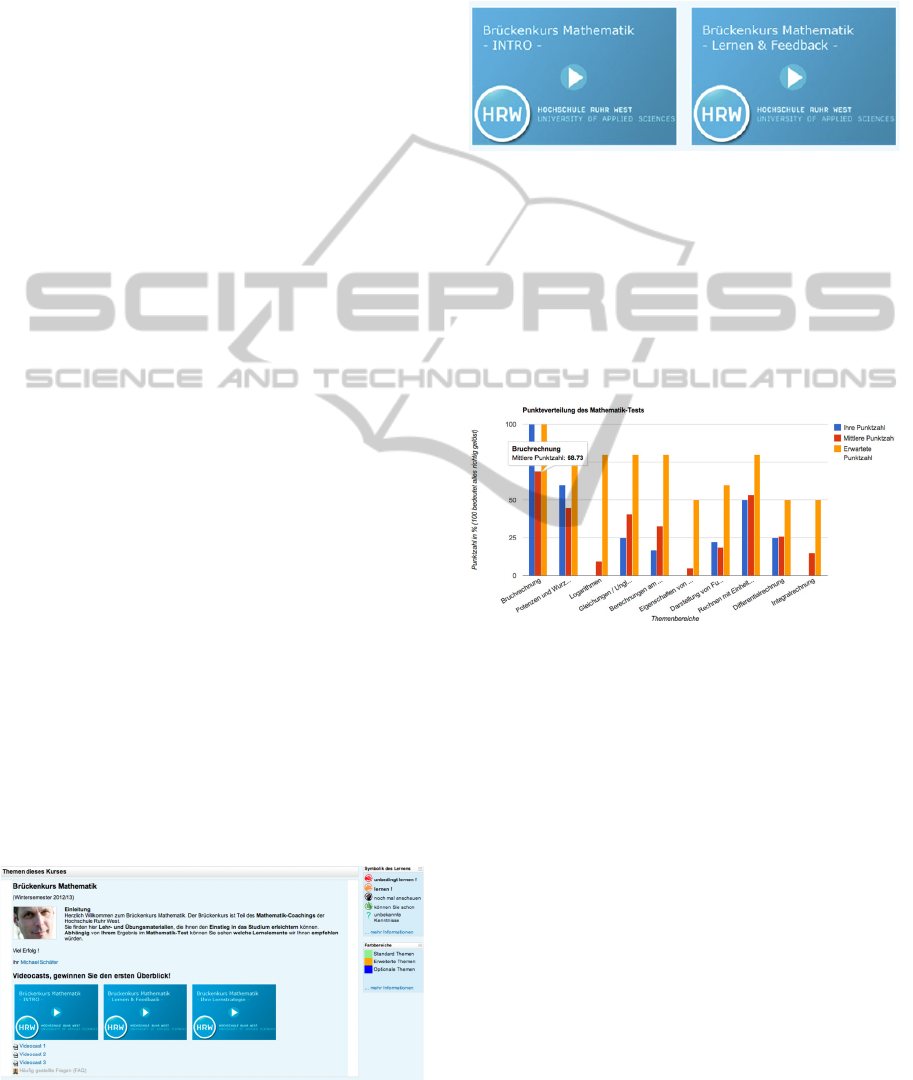
Figure 1.
Figure 1: Front page of the mathematical online course.
It gains attention by personally addressing the
student and by using motivating screencasts (Figure
2), which reflects the important of mathematical
knowledge and guides the students through the next
steps.
Figure 2: Screen casts as motivational elements.
They are invited to look at their personal test
score as starting point for their own self-regulated
learning concept.
As shown in Figure 3 the students can see their
own score, the average score of all students and the
expected score the university teachers have. For
simplicity reasons, the scores are clustered by topics
equal to Table 2.
Figure 3: Personal math test result (Blue (first column) –
own score of the student (depending on Moodle user), Red
(second column) – average score of all students, Orange
(third column) – expected score by teachers).
Having had a look at this first feedback, the
students are invited to watch the second screencast
about learning and feedback (Figure 2). Here they
are informed about the feedback symbolism like for
example the thumbs to reflect the results of the
mathematical test in the current subject. Like the
good knowledge of the student with the green thumb
up at the top of Figure 4. After reading these
explanations the students are guided to pass the first
learning element and to do the first mathematical
self-test.
A graphical rating scale gives them feedback on
their success and the students can prove this by
doing a second similar test.
An example is shown in Figure 4.
CSEDU2013-5thInternationalConferenceonComputerSupportedEducation
486
Figure 4: Feedback elements in the online course.
To enhance the engagement and the average
length of course-usage an avatar is embedded. This
virtual coach, implemented as 3D humanoid
character, is used to give feedback and learning
advice. Different implementations were evaluated.
On the one hand, a lean design of the automotive
sector as shown in Figure 5 with text-to-speech
translation, which could easily be used for dynamic
interactions (CharAt, Version 1.0) was tested. On
the other hand, pre-recorded but realistic 3D
animated humanoids with synchronized audio from
voice-over artists were tried.
Figure 5: Alex as virtual coach in the online course.
This was topped off with short mathematical
tests at the end of each week in the presence course
and a mathematical test at the end of the coaching
process, which is equivalent to the mathematical test
done before the coaching was started.
5 EVALUATION AND RESULTS
Three different data sources are used for evaluation.
Firstly, it was the log-data of the LMS to prove the
usage of the online mathematical course.
Secondly, the summative evaluation of learning
outcome based on the mathematical tests before and
after the coaching was used.
Thirdly, the formative evaluation one month
after the end of the coaching to evaluate the whole
system was taken into account.
5.1 Log Data
An anonymous ID and an email address were
collected with the mathematical test done in the
beginning. Due to data privacy policies it was not
allowed to use the data from matriculation. With this
data, 613 individual mails with the accounts to the
online course were generated. 32 mails came back
with failure notices. About 50 mails were suspended
to the spam-folders of the recipients by one email-
provider. We suppose that a significant part was not
read, because of the communication shifts from
email to other channels like social media platforms.
In the online course 493 students watched their
personal result as shown in Figure 3. The first
videocast was watched by 191 students (1200 page
views), the first learning element (elementary
calculation) was used by 286 students, the second
from 282 (powers and radicals) students, the fifth
(function) was only used by 149 students. The usage
of selftests have the same tendency from 155
students using the first selftest to 24 students using
the eleventh selftest.
5.2 Summative Evaluation
In the beginning n=613 of all new students took part
in the voluntary mathematical test. This is only a
part of all new students (N=893), because the
matriculation was possible until the first day of
studies. The information about the mathematical
coaching and the account to the online course were
sent to the students one month prior to the start of
studies and the presence course started three weeks
before the studies began.
5.2.1 Results before Coaching
Out of 48 items an average value of AVG=13.70
items were correctly solved with a standard
deviation of SD=8.82.
5.2.2 Results after Coaching
After our coaching the students could pass another
mathematical test with 48 equivalent items (n=132).
The results are based on a paired-samples t-test.
The average value of correctly solved items was
AVG=28.48 with a standard deviation of SD=7.31.
Depending on the kind of eligibility of university
admission, the following differences between the
different groups are to be found:
a) General eligibility with advanced mathematic
course
n=41, AVG=31.90, SD=8.71
KnowledgeControlledMathematicalCoaching-StrategiesandResultsofaPersonalizedBlendedLearningApproach
487

b) General eligibility with basic mathematic course
n=37, AVG=28.51, SD=8.07
c) Subject-linked eligibility
n=50, AVG=26.20, SD=8.69
5.3 Formative Evaluation
A formative assessment is done one month after the
studies start to evaluate the usability, acceptance and
performance of the coaching-system. The survey
consists of 27 items with 12 different dimensions.
The first evaluation in 2011 was only done with a
small part of the participating students (N=49). First
of all we were not sure, if a mathematical test,
before the studies are starting, will be accepted.
With an average value of AVG=5.42, a standard
deviation of SD=.93 and a median of SM=6 the
students seem to accept the test as reasonable.
Visiting the presence learning courses was profitable
for the students with an average value of AVG=5.84,
a standard deviation of SD=1.25 and a median of
SM=6. In a 5-level-Likert scale (Likert, 1932) the
students estimate the influence of the small group-
sizes with an average of AVG=1.7 and a standard
deviation of SD=1.37 (1: very positive, 2:
positive...).
For the question, if using the e-learning platform
was profitable to them, the students estimated with
an average of AVG=3.74, a standard deviation of
SD=1.39 and a median of SM=4. So only a slightly
positive result was measurable. Whereas the visiting
of the presence-learning course in combination with
using the e-learning platform was profitable for the
students with an average of AVG=4.93, a standard
deviation of SD=1.47 and a median of SM=5.
The overall feedback for fitting the demands of
each student, self-observed learning effects and
helpfulness for the first year courses was positive.
We used these results to improve our online-system
as shown before.
6 CONCLUSIONS AND
FURTHER WORK
The knowledge controlled mathematic coaching
concept was successfully implemented. The
summative evaluation shows a significant increase
of the mathematical competences of new students
prior to the beginning of their studies.
We plan to use our results to further enhance the
concept to improve the mathematical competence of
the students and the technical implementation. The
adaption of e-learning material, the personalized
feedback and the arrangement of learning groups
depending on the students’ competence have
positive effects on the improvement of current math
skills of first year students. The enhancement
through avatars seems to be promising.
In conclusion, this paper presented the
implementation of a learner centred adaptable
blended learning concept. The mathematical
coaching significantly improves learning effects.
These effects are controlled by summative and
formative evaluations. Some efforts of future work
are still necessary in order to enhance this concept
and optimise its implementation.
REFERENCES
Ayad, Khaled A. A. (2010). The role of edutainment in e-
learning - an empirical study. PhD Thesis, De
Montfort University.
Bhattacharya M., Hartnett M. (2008). Addressing
Diversity in Design of Online Courses. BCcampus and
Common wealth of Learning.
CharAt (Version 1.0)[Computer Software]. Cologne,
Germany: Charamel GmbH. Retrieved 02/02/2013,
from http://www.charamel.com/.
Deming, W. (1986). Out of the crisis: quality, productivity
and competitive position. Cambridge: Cambridge
University Press.
Jarvis, S.& de Freitas, S. (2009) Evaluation of an
Immersive Learning Programme to Support Triage
Training: In-game Feedback and its effect on Learning
Transfer. In proceedings of IEEE Games and Virtual
Worlds for Serious Applications (VS-GAMES ’09),
pp.117-122.
Keller, J. M. (2010). Motivational Design for Learning
and Performance: The ARCS Model Approach.
Springer US.
Knospe, H. (2012). Mathematik an der Schnittstelle
zwischen Schule und Hochschule Probleme und
Perspektiven. Retrieved 11/06/2012, from
http://www.nt.fh-koeln.de.
Likert, R. (1932). A Technique for the Measurement of
Attitudes. Archives of Psychology 140: 1–55.
Moodle Development Team. (2012). Modular Object
Oriented Dynamic Learning Environment, Open
Source LMS. Retrieved 01/11/2012, from
http://www.moodle.org.
Saul, C. & Wuttke, H.-D. (2011). Feedback
personalization as prerequisite for assessing higher-
order thinking skills. European Journal of Open,
Distance and E-learning, EURODL, pp. 445/1-445/10.
Schäfer M., Jansen M., Stehling T. (2012). Improving
Current Math State of Knowledge for First Year
Students, Proceedings of the 1st International Moodle
Scientific Conference (MoodleSCo2012), 2012
CSEDU2013-5thInternationalConferenceonComputerSupportedEducation
488
