
Model-based System Engineering for Fault Tree Generation and
Analysis
Nataliya Yakymets, Hadi Jaber, Agnes Lanusse
CEA Saclay Nano-INNOV, Institut CARNOT CEA LIST, DILS, 91 191 Gif sur Yvette CEDEX, Saclay, France
Keywords: Model-based System Engineering, Model-based Safety Assessment, Fault Tree, Sysml, Altarica.
Abstract: In this paper, we focus on the integration of formal approaches for automatic FT generation within a MBSE
workflow. We describe a safety modelling framework for FT generation that leverages features of SysML
modelling language and includes facilities to make semantic connections with formal verification and FTA
tools. MBSE methods and tools (meta-models, profiles, model transformation) are fully exploited to
propose a seamless workflow customizable for safety engineers. We illustrate the FT generation and
analysis flow associated with the proposed framework using the example of the train detection system and
the AltaRica formal environment.
1 INTRODUCTION
Safety-critical systems are expected to satisfy a high
level of dependability including reliability,
availability, security and safety. Therefore standards
concerned with the development of such systems
require an application of specific design flows where
system engineering is conducted in parallel with
various safety assessment (SA) activities. Typical
SA methods include hazard analysis, failure mode
and effects analysis (FMEA), fault-tree generation
and analysis (FTA) (NASA, 2002), formal
verification (Meenakshi et al., 2007). Although these
well-established methods provide an efficient
support for safety engineers, they could greatly
benefit from a tighter coupling with system
modelling environments.
In this context, model-based system engineering
(MBSE) is a convenient approach to develop safety-
critical systems (Estefan and May, 2007). MBSE
relies upon system level models and offers
convenient frameworks to integrate different
dedicated analysis views within a global design
environment. It becomes thus possible to perform
model-based safety analysis by incorporating
existing SA methods and tools into the MBSE
workflow.
In this paper, we aim to contribute in integration
of SA techniques into the MBSE environment based
on System Modelling Language (SysML) (OMG,
2007). SysML is a general-purpose modelling
language that provides a global overview of system
architecture. SysML is built as a UML profile for
specifying, analyzing, designing and verifying
complex systems. Certain efforts have already been
put into investigation of possible ways of SA
application through the MBSE process based on
SysML (David et al., 2010). Similar studies are also
undertaken with other modelling languages such as
Architecture Analysis and Design Language
(AADL) (Feiler et al., 2012) or EAST-ADL.
In this paper, we address formal approaches
applied for automatic FT generation and analysis at
the preliminary safety assessment phase. We
leverage features of SysML to capture information
required to conduct formal analysis in MBSE. For
this reason, we propose a safety modelling
framework for FT generation and analysis (SMF-
FTA) including metamodels, profiles, model
transformation, verification and FTA tools. The FTA
results can be further used for the evaluation of
different system architectures and their optimization
according to certain safety goals.
The remainder of the paper is organized as
follows. In section 2, we explore state-of-the-art in
SA techniques and tools for FTA. In section 3, we
introduce our method and toolset for automatic FT
generation and analysis. In section 4, we present
experimental results and conclude in section 5.
210
Yakymets N., Jaber H. and Lanusse A..
Model-based System Engineering for Fault Tree Generation and Analysis.
DOI: 10.5220/0004346902100214
In Proceedings of the 1st International Conference on Model-Driven Engineering and Software Development (MODELSWARD-2013), pages 210-214
ISBN: 978-989-8565-42-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORKS AND PAPER
CONTRIBUTION
FTA is a deductive top-down method to analyse
system design and safety. Typical FT consists of the
top event and a set of basic and house events
organized with logic gates. The FT qualitative
analysis aims to find all the minimal combinations
of basic events (called minimal cut sets) resulting in
the top event. The quantitative analysis of FTs is
also often used in probabilistic computation
performed by such tools as XFTA (XFTA, 2011).
The FT generation approaches fall into several
categories. Structured approaches (NASA, 2002)
use manually created models of failure behaviour.
Such approaches rely upon the ability of the SA
engineer to predict the system behaviour and,
consequently, may lead to higher probablity of
errors. Another group of FT generation approaches
(for example, HiP-HOPS (Walker et al., 2007) is
based on the use of analytical expressions associated
with the system components to model the possible
propagation of failures. Approaches based on failure
modes injection extend each component of the
nominal system model with a set of possible failure
modes and then model the system failure behaviour
using such an extended model. The tools based on
these approaches (for example, FSAP/NuSMV
(Bozzano and Villafiorita, 2007)) translate an
extended model into a state machine and then use
formal verification algorithms to generate FTs. We
list here only academic approaches, since industrial
solutions generally rely on part of them. Although
tools mentioned above (Walker et al., 2007),
(Bozzano Villafiorita, 2007) perform automatic FT
generation, they lack convenient representation of
the input system models and final results of SA. For
example, FSAP/NuSMV or ARC (ARC, 2012) tools
use formal languages such as SMV or AltaRica to
describe a system which might require certain time
efforts from the SA engineer. In HiP-HOPS, safety
annotations can be entered through a profile of the
EAST-ADL implementation in Papyrus, but there
are no elaborated mechanisms to show the results of
SA in the system models.
In this work we analyze the possibilities of using
different methods and tools for automatic FT
generation, analysis and visualization across the
MBSE process. We propose to combine the
analytical approach with formal verification methods
to automatically generate FTs derived from the
SysML models. We represent a safety modelling
framework for FT generation and analysis, called
SMF-FTA. SMF-FTA enables the use of formal
verification and FTA algorithms during the MBSE
process supported by the Papyrus (Papyrus, 2012)
editing tool for SysML. Furthermore, it implements
an ability to visualize FTA results in the SysML
modelling environment. SMF-FTA contains model
transformation tools, the ARC tool for formal
verification and the XFTA tool for FTA, as well as
the AltaRica (Arnold et al., 2000) and Open-PSA
(Open-PSA, 2008) metamodels and the profile for
FT visualization. In the next sections, we shall
describe the SMF-FTA architecture and show how
the tool can be used for the FT generation and
analysis.
3 SAFETY MODELLING
FRAMEWORK
The architecture of SMF-FTA is represented in
Figure 1. It has been implemented using java under
Eclipse Modelling Framework (EMF) and includes a
set of tools for FT generation and analysis. The FT
generation method and tool flow associated with
SMF-FTA include several steps. First, a system
under analysis is designed with Papyrus platform
using SysML block and internal block diagrams.
Then a SysML model of a system is annotated with
the possible failure behaviour. Once the annotation
has been done, the failure modes of every block are
automatically extracted from the output deviation
expressions, and the SysML model is converted into
the AltaRica language. The checking of the AltaRica
model is performed by the ARC tool using an
automatically generated script. This script allows
ARC to generate minimal cut sets for the considered
model. Based on this information we automatically
create FTs and represent them in the Open-PSA
format. Finally, with the XFTA tool we can perform
FT quantitative analysis. In order to make SA results
more representative, we visualize FTs in SysML
modelling environment using dedicated FT profile.
Figure 1: The SMF-FTA architecture.
Model-basedSystemEngineeringforFaultTreeGenerationandAnalysis
211

3.1 Model Annotation
A model is described in SysML using block and
internal block diagrams that can be further annotated
with system failure behaviour. This behaviour is
represented as a set of analytical expressions
showing how deviations in the block outputs can be
caused by internal failures of the block and/or
possible deviations in the block inputs. We assign
output deviation expressions by adding
OpaqueExpressions into the Default Description of
output ports of the appropriate block.
3.2 Model Conversion
The transformation method used for conversion of
SysML model to AltaRica relies upon the MBSE
approach. First, a SysML model is verified if it
conforms to the standard SysML metamodel and
then model to model transformation takes place. In
order to verify if a new generated AltaRica model
conforms to the AltaRica concepts, we developed
the AltaRica metamodel using Ecore package for
EMF.
Table 1: Transformation rules.
Concept SysML AltaRica Description
Component type System Block Node main
System under
analysis
Component
/Prototype
Block
Part
Node
Field:sub
System components
Flow variable
/Type
/Direction
FlowPort
/Flow Port Type
/Flow Direction
Field: Flow
/bool, integer, float,
domain
/In , Out
System ports
Connection
components
Connector Assertion
Connection between
components
Output deviation
expression
Opaque-Expression
Failure modes, failure
events, output
assertions
Block dysfunctional
behaviour
Table 1 lists the transformation rules used in the
algorithm implemented in SMF-FTA. In AltaRica, a
system is represented as a state machine composed
of the set of nodes N = {n
0
, n
1
,..., n
m
}. Each node n
i
= {F
in
, F
out
, S, E, T, A} contains a set of input F
in
and
F
out
output flows, a set of states S a set of events E a
set of transitions T and a set of output assertions A.
In SysML, a system can be considered as a set of
blocks B = {b
0
, b
1
,..., b
m
}, where each block b
i
=
{P
in
, P
out
, D}
contains a set of input P
in
and output
P
out
ports as well as a set of output deviation
expressions D linked to the output ports of the
blocks. Each expression contains a set of failure
modes M and a subset of corrupted inputs P'
in
of
block b
i
:
d
k
D, d
k
= {M, P'
in
P
in
}.
Consequently, each block b
i
of the SysML model
is translated into the AltaRica node n
i
as follows.
The input and output ports are translated into the
corresponding flows: P
in
→ F
in
, P
out
→ F
out
. Failure
modes extracted from the output deviation
expressions are converted into the node’s states and
events appearing during the transition to these states:
M→S, M→E. We assume that a system under
consideration is operating normally, thus all
extracted states are initialized as “false” in AltaRica.
The node’s transition
t
j
T is generated the
following way: (s
a
=false) |- e → (s
a
=true), where e
E is an event resulting in the occurrence of failure
mode associated with the state s
a
S.
In AltaRica, the correct behaviour of the nodes is
described using analytical expressions. These
expressions are simply a logical negation of output
deviation expressions:
D
→A.
3.3 Fault Tree Generation and Analysis
SMF-FTA exploits formal algorithms realised in the
ARC tool to generate all possible minimal
combinations of component failures violating a
given failure event. This allows us to group these
combinations, called minimal cut sets, in a fault tree
structure as follows. The events from each minimal
cut set are considered as basic and grouped using
AND gates. Then we connect all the AND gates to
the OR gate which, in turn, is linked to the top event.
Thereby, we provide a convenient way of
representing series of events that result in occurrence
of a considered top event.
FTs are generated in open-PSA format and can
be further analyzed with XFTA tool. This tool
performs quantitative analysis of FTs and provides
information on top event probability for different
mission times, importance factors of basic events,
common cause analysis, etc. The FTs can be
represented either in open-PSA format, the FT
specific format developed for describing complex
FTs, or in a graphical form with dedicated SysML
profile.
4 EXAMPLE OF SMF-FTA USE
In this section, we illustrate the FT generation and
analysis flow associated with SMF-FTA. We
consider an example of a train detection system
(TDS) that has been studied in (Andrews and Henry,
1997). The system shown in Figure 2 describes a
situation when there is no train in the section. In this
case generator G1 excites Relay core, which in turn
attracts the Contacts, so that Signal Circuit for
Green light is closed. Thus, Green light is on and
Red light is off. We consider a situation when “The
MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
212
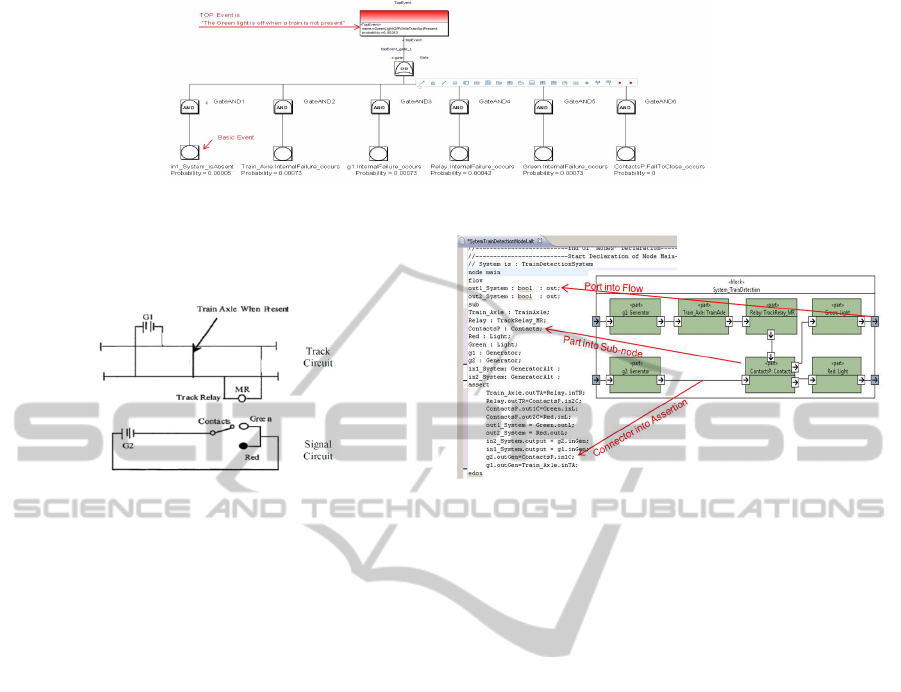
Figure 4: FT representation using Open-PSA subprofile.
Green light is off when a train is not present”. In
other words, this will be a top event of the FT.
Figure 2: Train detection system.
In Figure 3b we represent the TDS architecture
described using SysML internal block diagrams.
Having created a SysML model of TDS, we annotate
output ports of each block with output deviation
expressions. Information on the failure modes and
events is extracted from these expressions when the
SysML model is converted into AltaRica according
to the rules given in Table 1. The results of such a
transformation are shown for the main node of
AltaRica model (Figure 3).
We use ARC to build a FT corresponding to the
considered top event. This FT can be also
represented in a graphical form using our FT profile
(Figure 4). As shown in the FT, the top event occurs
if any of the G1, Train_Axle, Relay, ContactsP or
Green components fails. A quantitative analysis of
the obtained FT is conducted with the XFTA tool.
As an example, we assess the probability of the top
event based on the failure rates of basic events. We
find that the probability that “The Green light is off
when a train is not present” equals 2.63×10
-3
.
5 CONCLUSIONS
In this paper, we addressed the problem of the
integration of formal approaches for automatic fault
tree generation within a SysML-based engineering
workflow. We described a safety modelling
framework for fault tree generation, analysis and
visualization providing a convenient and uniform
a) b)
Figure 3: a) Main node declaration in AltaRica; b) Internal
block diagram of TDS.
environment for safety engineers by automating
certain phases of the safety assessment process.
ACKNOWLEDGEMENTS
We thank Hadi Jaber for his strong contribution to
this work during his internship in CEA.
REFERENCES
Andrews, J. D. & Henry, J. J., 1997. A computerized fault
tree construction methodology', Proceedings of the
Institution of Mechanical Engineers, Part E: Journal
of Process Mechanical Engineering 211(3), 171-183.
ARC (2012), 'ARC web page, available at: http://
www.altarica.labri.fr/forge/projects/arc/wiki.
Arnold, A.; Griffault, A.; Point, G. & Rauzy, A., 2000.
The AltaRica language and its semantics, Fundamenta
Informaticae 34, 109--124.
Bozzano, M. & Villafiorita, A., 2007. The FSAP/NuSMV-
SA Safety Analysis Platform, International Journal on
Software Tools for Technology Transfer 9, 5-24.
David, P.; Idasiak, V. & Kratz, F., 2010. Reliability study
of complex physical systems using SysML, Reliability
Engineering & System Safety 95(4), 431 - 450.
Estefan, J., May 2007. Survey of Candidate Model-Based
Systems Engineering (MBSE) Methodologies, rev. A,
IncoseMBSE Focus Group, . Passadena, CA, USA,
Model-basedSystemEngineeringforFaultTreeGenerationandAnalysis
213

(INCOSE), May 23, 2008. INCOSE-TD-2007-003-02.
Feiler, P. & Gluch, D.Professional, A.-W., ed., 2012.
Model-Based Engineering with AADL: An
Introduction to the SAE Architecture Analysis &
Design Language, P.Ed Heg USA.
NASA, 2002. Fault Tree Handbook with Aerospace
Applications Version 1.1.
Meenakshi, B.; Das Barman, K.; Babu, K. & Sehgal, K.,
2007. Formal safety analysis of mode transitions in
aircraft flight control system, in ‘DASC '07.
IEEE/AIAA 26th', pp. 2.C.1-1 -2.C.1-11.
OMG, 2007. Object Management Group - Systems
Modeling Language (OMG SysML).
OPEN-PSA, 2008. OPEN-PSA web page, available at:
http://www.open-psa.org'.
Papyrus, 2012. Papyrus web page, available at: http://
www.eclipse.org/modeling/mdt/papyrus/.
Walker, M.; Bottaci, L. & Papadopoulos, Y., 2007.
Compositional Temporal Fault Tree Analysis, in
Francesca Saglietti & Norbert Oster, ed., 'Computer
Safety, Reliability, and Security', Springer Berlin
Heidelberg, pp. 106-119.
XFTA, 2011. XFTA web page, available at: http://
www.lix.polytechnique.fr/~rauzy/xfta/xfta.htm
MODELSWARD2013-InternationalConferenceonModel-DrivenEngineeringandSoftwareDevelopment
214
