Enhancing Estimation Skills with GeoGebra

Volume Ratios of Essential Solids

Libu

se Samkov

Department of Mathematics, Faculty of Education, University of South Bohemia,

Jeron

ymova 10,

Cesk

e Bud

ejovice, Czech Republic

Keywords:

Volume Ratios, Estimation Skills, GeoGebra, ICT Support.

Abstract:

The ﬁrst part of this article reports the results of a survey focusing on estimation skills relating to the concept of

volume. The survey tested pre-service and in-service math teachers of various nationalities and various school

types, and investigated their skills in estimating volume ratios of essential solids (a cylinder, a ball, and a cone).

The second part of the article analyzes the mathematical background of cone and ball cases. The third part of

the article shows the possibilities of GeoGebra software in creating test materials for similar surveys, and —

in accordance with the results of the survey — presents dynamic models designed to enhance estimation skills

in volume ratios. The text gives detailed instruction on how to create such kind of GeoGebra materials.

1 INTRODUCTION

Estimation is a process whereby one approximates,

through rough calculations, the worth, size, or amount

of an object or quantity that is present in a given situ-

ation. The approximation, or estimate, is a value that

is deemed close enough to the exact value or mea-

surement to answer the question being posed (NCES,

1999). The importance of estimation in the school

curriculum was acknowledged for instance in the

1986 yearbook of National Council of Teachers of

Mathematics, see (Schoen and Zweng, 1986). The

acquiring of estimation skills in schools is said to pro-

vide an essential practical means of operating within

many mathematical and everyday situations in which

precise calculation or measurement are contextually

deﬁned as either impossible or unnecessary (Levine,

1982).

This article focuses on estimation skills re-

lated to the concept of volume, that means on the

measurement-type estimation skills. It is particularly

devoted to estimating volume ratios. The issue can be

represented by the question

“What are the corresponding height and vol-

ume ratios of a given solid?”

Precisely, for a given solid and for a given volume ra-

tio m/n we explore the level to which the solid should

be ﬁlled with water in order to ﬁll exactly m/n of the

solid volume. This level is speciﬁed relatively, as a

ratio of the height of the solid. We may also study the

issue conversely — ﬁll the solid to a given height ratio

α, and look for the volume of the ﬁlled part expressed

as a ratio of the volume of the whole solid.

The issue of volume ratios is not a common part

of school mathematics, due to difﬁcult calculations

backgrounding the problem. On the other side, vol-

ume ratios are an integral part of everyday reality. To-

gether it makes the issue an ideal candidate for engag-

ing estimates.

The ﬁrst part of this article reports the results of

a survey focusing on volume ratios of three essential

solids: a cylinder, a ball, and a cone. See Figure 1.

The survey tested 80 pre-service and in-service math

teachers of various nationalities and various school

types, and investigated their skills in estimating vol-

ume ratios of these solids.

Figure 1: Solids ﬁlled with water to a certain level.

The second part of the article analyzes the mathe-

matical background of cone and ball cases.

The third part of the article shows the possibilities

of GeoGebra software in creating test materials for

similar surveys, and — in accordance with the results

of the survey — presents dynamic models designed to

enhance estimation skills in volume ratios. The text

Samková L..

Enhancing Estimation Skills with GeoGebra - Volume Ratios of Essential Solids.

DOI: 10.5220/0004382100890094

In Proceedings of the 5th International Conference on Computer Supported Education (CSEDU-2013), pages 89-94

ISBN: 978-989-8565-53-2

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

gives detailed instruction on how to create such kind

of GeoGebra materials.

2 THE SURVEY

2.1 The Sample

We tested 37 in-service math teachers, namely 11 uni-

versity teachers and teacher trainers from Czechia,

Germany, Serbia and Bulgaria, and 26 teachers

from Czech, German and Serbian primary, lower-

secondary and upper-secondary schools. These teach-

ers were participants in workshops at some confer-

ences and training seminars held between November

2011 and October 2012.

Concurrently we tested 43 pre-service math teach-

ers from Czech and German universities. These

teacher students were not individually selected; the

survey was conducted in whole classes.

2.2 The Test

All surveyed teachers got to ﬁll the same worksheet,

consisting of 17 quick-answer questions with a com-

mon instruction. These questions were open-ended.

The worksheet is precisely shown in Figures 2-5.

Figure 2: The worksheet, a title page.

Figure 3: The worksheet, a cylinder page.

The content of the worksheet is of escalating dif-

ﬁculty. It begins with a cylinder case, which serves as

a kind of calibration — all volume ratios of a cylin-

der are identical to height ratios. Then the worksheet

Figure 4: The worksheet, a ball page.

Figure 5: The worksheet, a cone page.

continues with a ball, whose height and volume ratios

coincide only in 1/2 case. The ﬁnal part of the work-

sheet is devoted to a cone, in which all height ratios

differ from their corresponding volume ratios.

2.3 The Evaluation

We divided respondents into 2 groups according to

their status (in-service, pre-service).

We focused on relative errors of estimates calcu-

lated as

estimate − exact answer

exact answer

(1)

so that the sign can tell us if the estimate is bigger

than the exact answer (+ sign) or smaller (− sign).

As the ﬁrst evaluation method we ascertained

relative errors of all outcome estimates, and deter-

mined their arithmetic mean and median. A detailed

overview can be found in Table 1.

The table shows that both in-service and pre-

service teacher respondents have good estimation

skills in a cylinder case, and also in a ball case — ex-

cept 1/10 of the ball volume. Both groups overrated

1/10 of the ball volume, in-service performed a little

better, their mean relative error is 44 %. Also both

medians are overrated in this case.

On the other side, cone estimates are generally un-

derrated, for all tested volume ratios. The worst cone

ratio was 1/2 (with mean relative error -33 %, resp.

-32 %), closely followed by 1/4 (with both mean rel-

ative errors -29 %).

Since the variability of answers was limited by

the requirement to express volume ratios as fractions,

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

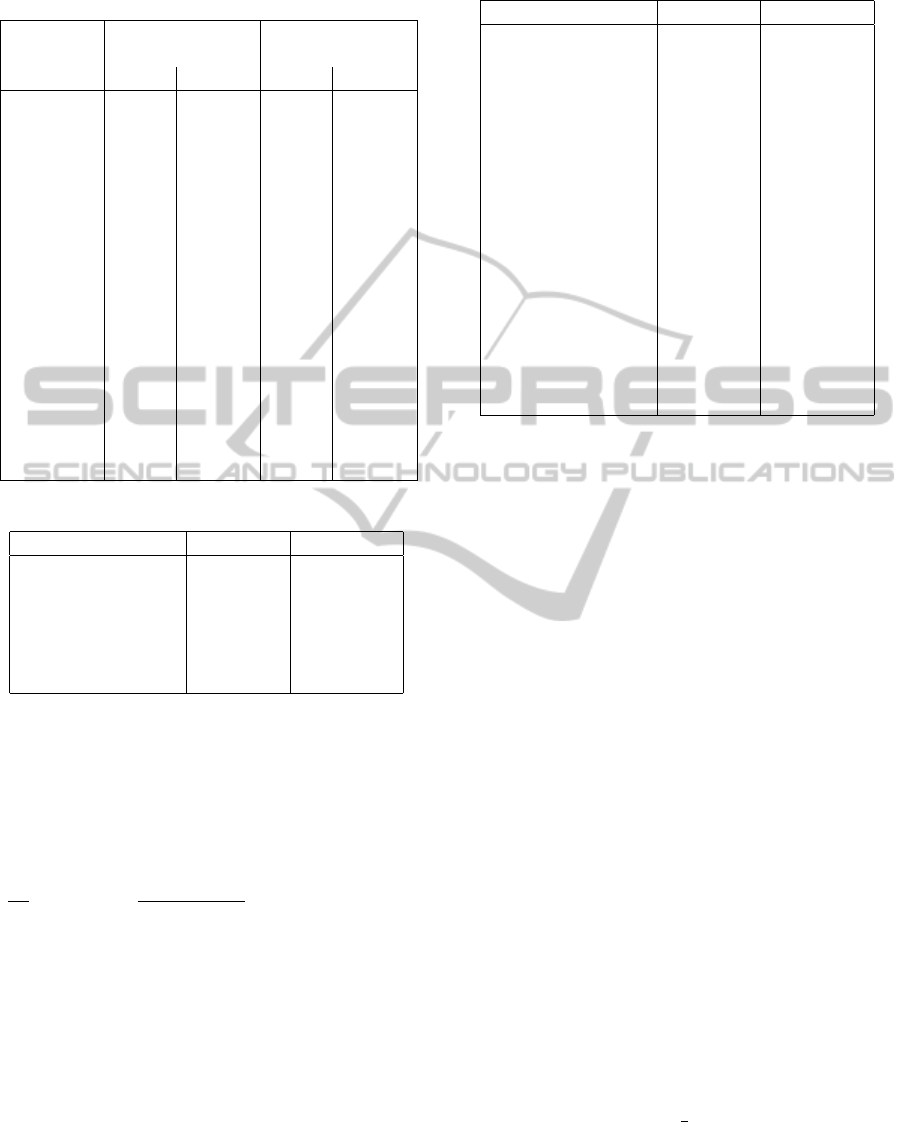
Table 1: Relative errors of in-service and pre-service teach-

ers’ estimates; in-service: N = 37, pre-service: N = 43.

Solid & In-service Pre-service

volume ——————- ——————-

ratio Mean Median Mean Median

Cylin 1/2 -1 % 0 % 0 % 0 %

Cylin 1/5 -2 % 0 % 0 % 0 %

Cylin 3/4 1 % 0 % 1 % 0 %

Cylin 3/5 3 % 0 % 3 % 0 %

Cylin 7/8 -7 % 0 % 0 % 0 %

Ball 1/2 0 % 0 % 0 % 0 %

Ball 1/3 8 % 0 % 5 % 0 %

Ball 1/4 8 % 0 % 14 % 6 %

Ball 1/5 15 % 0 % 7 % 0 %

Ball 2/3 -2 % 0 % -1 % 0 %

Ball 3/4 1 % 0 % -1 % 0 %

Ball 1/10 44 % 34 % 48 % 55 %

Cone 1/2 -33 % -33 % -32 % -33 %

Cone 1/4 -29 % -20 % -29 % -33 %

Cone 2/3 -30 % -25 % -28 % -25 %

Cone 3/4 -19 % -20 % -19 % -20 %

Cone 7/8 -15 % -14 % -14 % -14 %

Table 2: Modus of estimates.

Solid, volume ratio In-service Pre-service

Ball 1/10 1/6 1/5

Cone 1/2 1/3 1/3

Cone 1/4 1/5 1/6

Cone 2/3 1/2 1/2

Cone 3/4 3/5, 1/2 3/5

Cone 7/8 3/4 3/4

we may also focus on modus of our data. A detailed

overview of cases whose modus differs from the exact

answer is in Table 2.

We may also analyze the difference between

groups by independent two-sample t-test. Take for

example the samples of relative errors belonging to

Ball 1/10 picture. Formula

= 1,443 ∈



42,36

(0,025)

42,36

(0,025)



(2)

means that we do not reject the hypothesis of equal

variances at 0,05 level, and

T = 0, 399 5 t

(0,05) (3)

means that we do not reject the hypothesis of equal

means at 0,05 level either.

As the last method of evaluation we use the scor-

ing method for Estimation Interview Test used in

(Montague and van Garderen, 2003): an estimate is

considered accurate if it is within 50 % of the ex-

act answer. From this perspective, the case of 1/10

of the ball volume appears as the one with the high-

est failure rate: it has 17 inaccurate estimates among

Table 3: Percentage of inaccurate estimates.

Solid, volume ratio In-service Pre-service

Cylinder 1/2 0 % 0 %

Cylinder 1/5 3 % 0 %

Cylinder 3/4 0 % 0 %

Cylinder 3/5 0 % 2 %

Cylinder 7/8 8 % 2 %

Ball 1/2 0 % 0 %

Ball 1/3 6 % 9 %

Ball 1/4 11 % 23 %

Ball 1/5 11 % 7 %

Ball 2/3 0 % 9 %

Ball 3/4 0 % 7 %

Ball 1/10 47 % 54 %

Cone 1/2 6 % 21 %

Cone 1/4 25 % 28 %

Cone 2/3 6 % 7 %

Cone 3/4 8 % 19 %

Cone 7/8 6 % 9 %

in-service teachers’ answers (which means 47 % an-

swers being inaccurate), and 23 among pre-service

teachers’ answers (54 % inaccurate). The second one

in terms of failure is the case of 1/4 of the cone vol-

ume with 25 %, resp. 28 % inaccurate answers. A

detailed overview can be found in Table 3.

2.4 The Summary

The survey showed that both pre-service and in-

service math teachers had signiﬁcant difﬁculties with

estimating volume ratio from a picture of a cone, and

in some cases also from a picture of a ball.

It would be expedient to enhance this kind of esti-

mation skills, for instance through a suitable ICT en-

vironment.

3 MATHEMATICAL

BACKGROUND

This section shall reveal the mathematical back-

ground of the problem of ﬁnding the height ratio α

for a given volume ratio m/n, and vice versa.

3.1 The Cone

The volume of a cone with base radius r and height

k is given by a formula

πr

k. The water in the

cone reaches an unknown height h, expressed as an

α-multiple of the height of the cone, i.e., h = α · k.

The complement of the water in the cone is also a

cone, with height k(1 − α), and base radius r(1 − α).

EnhancingEstimationSkillswithGeoGebra-VolumeRatiosofEssentialSolids

See Figure 6. Thus, the volume of the water can be

expressed as

water

πr

k −

πr

(1 − α)

k(1 − α)

πr



1 − (1 − α)



(4)

Figure 6: The cone (left), similar triangles (middle, right).

We are looking for a water level corresponding to

m/n of the cone volume:

water

· V

cone

1 − (1 − α)

(5)

α = 1 −

1 −

(6)

3.2 The Ball

The volume of a ball with radius r is given by a for-

mula

πr

. The height of the ball equals 2r. The wa-

ter in the ball reaches an unknown height h = α · 2r.

The water in the ball occupies a spherical cap with

height h, for details see Figure 7.

Figure 7: The ball situation in detail.

The volume of the water equals the volume of the

spherical cup, that means

water

πh(3a

+ h

) =

πr

(3 − 2α) (7)

We are looking for a water level corresponding to

m/n of the ball volume:

water

· V

ball

(3 − 2α) =

(8)

2α

− 3α

= 0 (9)

This cubic equation has three real solutions, one of

them belonging to an interval h0,1i:

α =

− cos



π + arccos



1 −





(10)

Detailed solution of (9) leading to (10) can be found

in (Samkova, 2012).

4 ICT SUPPORT

We shall show the possibilities of enhancing estima-

tion skills with help of ICT, both in passive and active

ways. We shall use GeoGebra, free mathematics dy-

namic software for teaching and learning mathemat-

ics at all school levels. GeoGebra is currently avail-

able in about 55 languages, it has received several

educational software awards in Europe and the USA.

For more about GeoGebra see (GeoGebra, 2012).

4.1 Creating Illustrations with

GeoGebra

At ﬁrst we shall demonstrate the passive way of Geo-

Gebra support — dynamic illustrations of transparent

hollow essential solids partially ﬁlled with water.

4.1.1 The Cylinder

The GeoGebra construction begins with sliders for n,

m, cylinder radius r, and cylinder height k. Then we

create a front view of the cylinder, which is actually a

rectangle with base 2r and height k:

poly1= Polygon[(r,0),(r,k),(-r,k),(-r,0)]

The ﬁlled part of the cylinder is also a cylinder, its

front view is another rectangle:

h=k*m/n

poly2=Polygon[(r,0),(r,h),(-r,h),(-r,0)]

The construction is almost done, we just have

to design it properly. We change LineThickness of

poly1 to 6, Color of poly2 to blue, LineThickness of

poly2 to 0, Opacity of poly2 to 50. The preview of

the construction is in Figure 8.

With this dynamic illustration we may prepare

various pictures of cylinders ﬁlled with water to a cer-

tain level, and export them as PNG or EPS ﬁles.

We may also export the dynamic worksheet as a

webpage, and make it available to students. In this

case, we label the r slider with “base radius”, and the

k slider with “cylinder height”. We add an interactive

text to the worksheet.

The ﬁnal form of the worksheet is in Figure 9.

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation

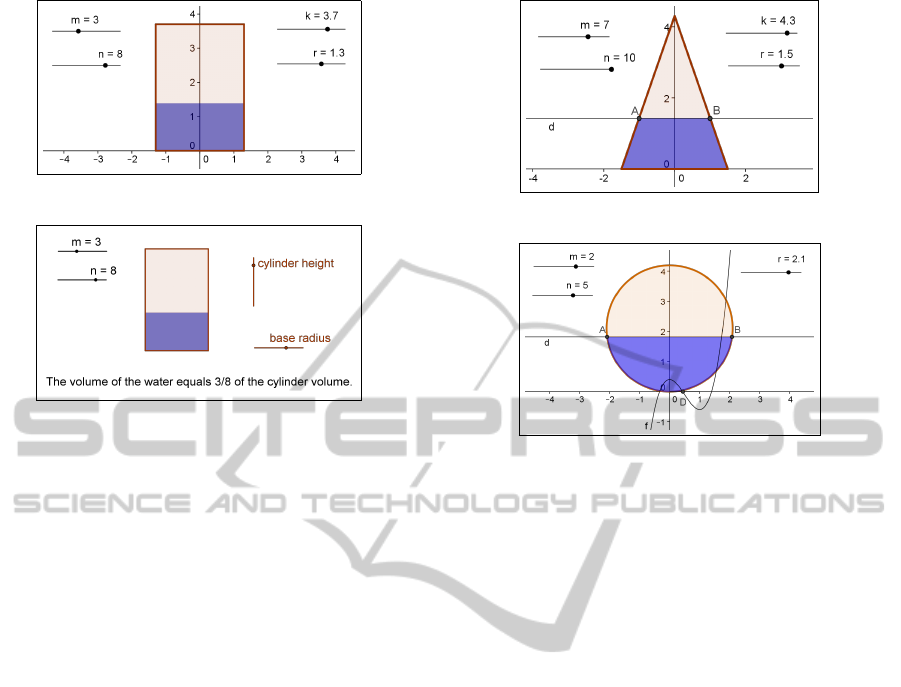
Figure 8: The preview of the cylinder case construction.

Figure 9: The dynamic worksheet for a cylinder.

4.1.2 The Cone

The construction begins again with sliders for n, m,

base radius r, and cone height k. Then we create a

front view of the cone, which is actually an isosceles

triangle with base 2r and height k:

poly1= Polygon[(r,0),(0,k),(-r,0)]

The ﬁlled part of the cone is a truncated cone, its

front view is an isosceles trapezoid:

alpha=1-(1-m/n)ˆ(1/3)

h=alpha*k

d=Line[(0,h),xAxis] . . . the water level

Intersect[d,poly1] . . . points A and B

poly2=Polygon[(r,0),B,A,(-r,0)]

Now we just have to design the picture the same

way as in the cylinder case. The preview of the con-

struction is in Figure 10.

Note that the illustration is not correct for m = n.

We have to create a blue triangle

poly3=Polygon[(r,0),(0,k),(-r,0)]

with a Condition to Show Object m=n.

4.1.3 The Ball

The construction begins again with sliders for n, m,

and ball radius r. Then we create a front view of the

ball, which is a circle with radius r:

circ1=Circle[(0,r),r]

As the next step we solve graphically the equation

(9): we deﬁne a left side as a function, and ﬁnd where

its graph intersect h0,1i at the x-axis:

f(x)=2xˆ 3-3xˆ 2+m/n

Figure 10: The preview of the cone case construction.

Figure 11: The preview of the ball case construction.

a=Segment[(0,0),(1,0)]

D=Intersect[f,a]

alpha=x(D)

The ﬁlled part of the ball is an upside-down ori-

ented spherical cup, its front view is a circular seg-

ment with a chord parallel to x-axis:

h=alpha*2r

d=Line[(0,h),xAxis] . . . the water level

Intersect[d,circ1] . . . points A and B

circ2=Arc[circ1,A,B]

As previously, we design the picture, and solve

separately the situation for m = n. The preview of the

construction is in Figure 11.

4.2 Interactive Estimation Training

with GeoGebra

Now we shall demonstrate the active way of Geo-

Gebra support — a dynamic GeoGebra worksheet for

interactive estimation training of volume ratios. This

tool focuses on the process of ﬁnding the right esti-

mate of water level for a given volume ratio. The

worksheet randomly generates volume ratios m/n,

waits for the user to draw his estimate to the picture,

and evaluates the estimate.

We shall show the construction in a cone case. The

construction begins with random sliders for n, m, with

sliders for r, k, and with poly1, alpha, h as in 4.1.2.

Then we create the exact water level:

d=Segment[(-2*r,h),(2*r,h)]

EnhancingEstimationSkillswithGeoGebra-VolumeRatiosofEssentialSolids

This exact answer should be hidden if needed, so that

we create a check box q with d as its selected object,

and label it Exact answer.

The next step will prepare the picture for user’s

estimation process:

p=Segment[(0,0),(0,k)]

P=Point[p]

o=Line[P,xAxis]

Intersect[o,poly1] . . . points A and B

poly2=Polygon[(r,0),B,A,(-r,0)]

The preview of the construction is in Figure 12.

Figure 12: The preview of the training construction.

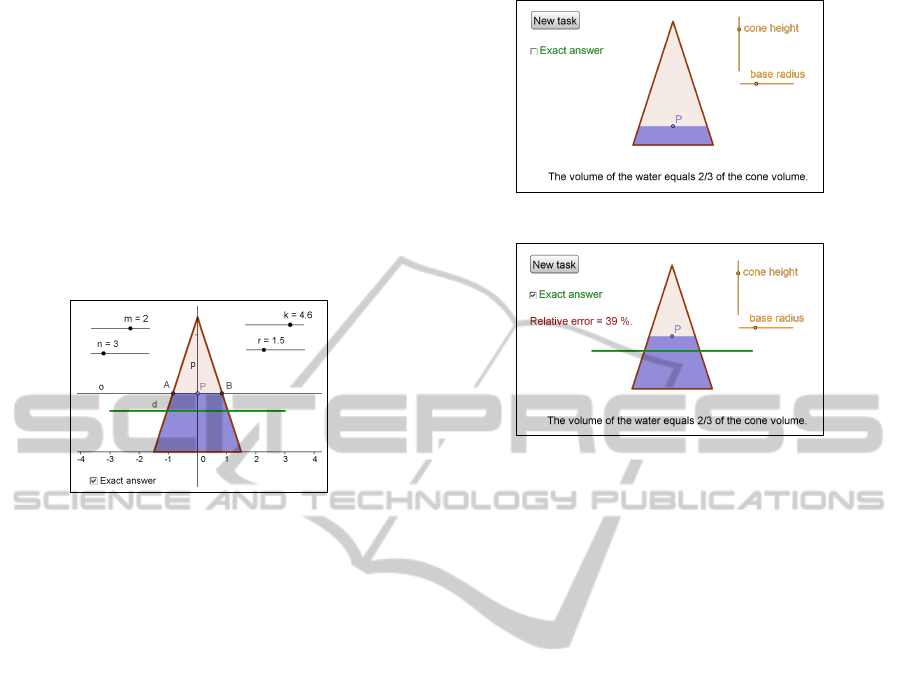
As a ﬁnal activity we have to manage the process

of generating random values of n, m: we create a but-

ton with label New task, and with GeoGebra script

UpdateConstruction[]

q=false

Pressing this button will load new random values

for n and m, and hide the segment with exact answer.

The user can move point P to a position where he

thinks the corresponding water level should be, then

mark the check box Exact answer, and compare his

estimate with the line of exact answer.

We may also determine relative error of the esti-

mate: deﬁne err=round((y(P)-h)/h*100), and in-

corporate it into an interactive text with a Condition

to Show Object q=true to it.

The ﬁnal form of the worksheet can be seen in

Figures 13 and 14.

5 CONCLUSIONS

The issue of volume ratios is a remarkable compo-

nent of the concept of volume. Our survey showed

that even math teachers had difﬁculties with estimat-

ing volume ratios of some essential solids. GeoGebra

software offers an interesting way how to enhance

this kind of estimation skills — through a dynamic

GeoGebra environment we can create illustrations re-

lated to the volume ratio issue, or an interactive es-

timation training tool. Future surveys may focus on

Figure 13: The worksheet ready for user’s estimation.

Figure 14: The evaluation of the user’s estimate.

non-teacher respondents or more deeply on the partic-

ular role of GeoGebra in enhancing estimation skills.

ACKNOWLEDGEMENTS

The survey described in the article was conducted

within a European FP7 project: The FIBONACCI

Project — Large scale dissemination of inquiry based

science and mathematics education, No. 244684.

REFERENCES

GeoGebra 4 available at http://www.geogebra.org, (re-

trieved Nov 5, 2012).

Levine, D. R. (1982). Strategy use and estimation ability of

college students. Journal for Research in Mathematics

Education, 13, 350-359.

Montague, M. and van Garderen, D. (2003). A Cross-

Sectional Study of Mathematics Achievement, Esti-

mation Skills, and Academic Self-Perception in Stu-

dents of Varying Ability. Journal of Learning Dis-

abilities, 36(5), 437-448.

National Center for Educational Statistics (1999). Estima-

tion Skills, Mathematics-in-Context, and Advanced

Skills in Mathematics. NCES 2000-451, Washington,

DC.

Samkova, L. (2012). Jak velk

a je t

retina koule? [In Czech:

How big is one third of a ball?] South Bohemia Math-

ematical Letters, 20(1). (to appear)

Schoen, H. and Zweng, M. (1986). Estimation and mental

calculations: The 1986 Yearbook of the NCTM. VA:

National Council of Teachers of Mathematics, Reston.

CSEDU2013-5thInternationalConferenceonComputerSupportedEducation