
Solving Planning Problems with LRTA*
Raulcezar M. F. Alves and Carlos R. Lopes
Faculty of Computing, Federal University of Uberlˆandia, Uberlˆandia, Minas Gerais, Brazil
Keywords:
Planning Systems, EHC, BFS, LRTA*, FF Planner.
Abstract:
A number of new heuristic search methods have been employed in the development of planning systems
over the last years. Enforced Hill Climbing (EHC) combined with a complete search strategy, such as Best
First Search (BFS), is a method that has been frequently used in several AI planning systems. Although
this method presents an enhanced performance when compared to alternative methods used in many of the
other planning domains, it does all the same show some weaknesses. In this paper the authors propose to
replace the use of EHC and BFS with LRTA*, which is a search algorithm guided by heuristics like EHC and
is as complete as BFS. Moreover, the authors implemented some optimizations on LRTA*, such as a heap
with a maximum capacity to store the states during the search, along with pruning of successors after state
expansion. Experiments show significant improvements compared to the standard form of the FF planner,
which is a representative planning system based on EHC and BFS.
1 INTRODUCTION
Planning is a field of Artificial Intelligence that tries
to control complex systems autonomously. It has be-
come very useful for solving practical problems such
as design, logistics, games, space exploration, etc.
Planning systems or planners aim to generate a se-
quence of actions, called a plan, required to reach a
goal (a solution of a problem) from a given initial con-
figuration of the problem.
Many planners use search techniques to select ac-
tions for building their plans such as the FF (Fast
Forward) planner that combines the execution of two
search algorithms: EHC (Enforced Hill Climbing)
and BFS (Best First Search). After performing sev-
eral experiments on problems of common planning
domains using FF, it was possible to identify some sit-
uations that could hamper the performance of search
algorithms. One situation happens when the search
process goes into a local maximum and gets stuck
at dead ends, which cause local search algorithms
as EHC to fail. Another situation refers to the lack
of memory space to store all the states generated by
complete search algorithms like BFS.
This paper presents a planning algorithm based on
a search algorithm known as LRTA* (Learning Real
Time A*). In order to overcome the difficulties de-
scribed above, we propose some modifications to the
standard LRTA* algorithm. A priority queue is used
to store generated states. States with high heuristic
values are placed near to the root, so they can be eas-
ily removed in case there is no memory space left.
Also we have introduced a policy for pruning succes-
sors rather than saving all of them after expanding a
state. An advantage of LRTA*, is that it can easily es-
cape from a local maximum, which is a problem for
local search techniques. The planning algorithm was
built upon JavaFF, a Java implementation of FF. Ex-
periments show significant improvements compared
to the standard form of the FF planner.
The remainder of the paper is organized as fol-
lows. Section 2 describes related work and motiva-
tion for our proposal. Definition and characteristics
of the problem to be solved are provided in section
3. Background knowledge is described in Section 4.
In section 5 we propose the HPS-LTRA* algorithm
to improve the planning process. A description of the
experiments and their results is provided in section 6.
The conclusion is presented in section 7.
2 RELATED WORK
In the last decade there was a significant increase in
the efficiency of planning systems. The FF planner is
the evolution of these systems. FF incorporated tech-
niques proposed by previous planners like HSP (Bon-
net and Geffner, 1998) which brought along some fur-
ther improvements.
475
M. F. Alves R. and R. Lopes C..
Solving Planning Problems with LRTA*.
DOI: 10.5220/0004449404750481
In Proceedings of the 15th International Conference on Enterprise Information Systems (ICEIS-2013), pages 475-481
ISBN: 978-989-8565-59-4
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

Just as HSP, the FF planner (Hoffmann and Nebel,
2001) carries out a forward state space search, using
a heuristic that estimates the goal distance by ignor-
ing the delete list of all actions. It is a very common
strategy used to relax the model and find a solution
with lower cost and fewer restrictions. Unlike HSP
that assumes subgoals to be independent, FF takes
into account positive interactions that might happen
among subgoals. Also, FF accepts the selection of
more than one action at a time by building a graph of
a relaxed plan, a technique based on the Graphplan
system (Blum and Furst, 1995).
Another difference between FF and HSP is the in-
troduction of a novel kind of local search strategy to
avoid local maximum, employing a systematic search
and HC (Hill Climbing) algorithm, called EHC (En-
forced Hill Climbing). The EHC was developed to use
the concept of helpful actions during the expansion of
a state. The employment of helpful actions works like
a filter to return a set with just promising successors
of a state.
FF was the most successful automatic planner
in the “2nd International Planning Competition”.
Metric-FF a descendant of FF, was a top performer in
STRIPS and simple numeric tracks of the next com-
petition. Recent planners such as Conformant-FF,
Contingent-FF, Probabilistc-FF, MACRO-FF, MAR-
VIN, POND, JavaFF, DiFF and Ffha have employed
strategies introduced by FF (Akramifar and Ghassem-
Sani, 2010).
In the same line of FF, other recent planners com-
bine several search techniques. For instance, FD
(Fast Downward) (Helmert, 2006) computes plans by
heuristic search in the state space reachable from the
initial state. However, FD uses a very differentheuris-
tic evaluation function called the causal graph heuris-
tic that does not ignore the delete list unlike HSP and
FF. FD also uses some optimizations in search algo-
rithms within its strategy, as described below:
• Greedy best-first search: a modified version
of (Russell and Norvig, 2009) greedy best-first
search, with a technique called deferred heuris-
tic evaluation to mitigate the negative influence of
wide branching. It also deals with preferred op-
erators introduced by FD, similar to FF’s helpful
actions.
• Multi-heuristic best-first search: a variation of
greedy best-first search which evaluates search
states using multiple heuristic estimators, main-
taining separate open lists for each, and support-
ing the use of preferred operators too.
• Focused iterative-broadening search: a new sim-
ple search algorithm that does not use heuristic es-
timators, and instead reduces the vast set of search
possibilities by focusing on a limited operator set
derived from the causal graph.
The LAMA planner (Richter and Westphal, 2010)
follows the same idea offered by the other systems
cited above, that being the heuristic forward search.
It presented the best performance among all plan-
ners in the sequential satisficing track of the “Inter-
national Planning Competition 2008”. LAMA uses
a variant of the FF heuristic and heuristic estimates
derived from landmarks, propositional formulas that
must be true in every solution of a planning task.
Two algorithms for heuristic search are implemented
in LAMA: a greedy best-first search, aimed at find-
ing a solution as quickly as possible; and a Weighted
A* search that allows balancing speed against solution
quality. Both algorithms are variations of the standard
methods, using open and closed lists.
The improvementmade to planning systems is not
only due to the advanceof heuristic functions, but also
to the creation and modification of search algorithms.
In (Akramifar and Ghassem-Sani, 2010), a new
form of enforced hill climbing, called GEHC (Guided
Enforced Hill Climbing) was proposed to avoid dead
ends during the search by adapting an ordering func-
tion to expands the successors. It is faster and ex-
amines fewer states than EHC, even though in some
domains its plan quality was slightly inferior.
An approach of action planning based on SA (Sim-
ulated Annealing) is described at (Rames Basilio Ju-
nior and Lopes, 2012), which shows significant re-
sults compared to algorithms based on enforced hill
climbing. One of the difficulties is to choose the val-
ues of the parameters used in SA.
(Xie et al., 2012) presents a method that use a
greedy best-first search driven by a combination of
random walks and direct state evaluation, which bal-
ances between exploration and exploitation. This
technique was implemented in the Arvand planner of
IPC-2011, which improved coverage and quality of
its standard form. The algorithm scales better than
other planners especially in domains in which many
paths are generated between the initial state and the
goal. However, it does not have a good performance
in problems that require exhaustive search of large re-
gions of the state space.
A variation of a best-first search algorithm is in-
troduced by (Stern et al., 2011), called PTS (Poten-
tial search), which is designed to solve a cost-bound
search problem. It orders the states in the open list
according to their potential that is generated by the
relation between a given heuristic and the optimal so-
lution cost. This algorithm showed good results in
relation to others that have a similar purpose, such as
those algorithms based on Weighted A*. But until the
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
476

desired solution is found, a state that has a slightly
higher potential but is farther from the goal is prefer-
able to a state that is very close to the goal.
In most of these works even with some modifica-
tions, the algorithms are not capable of finding the so-
lution for all problems by using only one search tech-
nique. In general, it is necessary to use a combination
of search techniques. When the main techniques fail
in achieving a solution, the planners make use of a
complete search to reach the goal in order to guaran-
tee completeness. As a result, much time and effort
are wasted in a preliminary phase of those planning
algorithms.
3 CHARACTERIZATION OF THE
PROBLEM
A planning problem is defined by a tuple of three el-
ements (A, I, G), where A is a set of actions, I refers
to the initial state, and G corresponds to a goal to be
achieved. Let P be the set of all propositions that rep-
resents facts in the world. The current state, or world,
is assigned to w and represents the subset of satis-
fied propositions in P so that w ⊆ P in the world. In
STRIPS (Fikes and Nilsson, 1971), an action is repre-
sented by a triple (pre(a), add(a), del(a)) whose elements
belong to the set of propositions P and corresponds
respectively to its preconditions and effects - this last
through the add and delete lists. Action a is applica-
ble in w if w ⊇ pre(a) holds. To apply a in w, replace
w with w’ so that w’ = w - del(a) + add(a). It is assumed
that del(a) ∩ add(a) = {}. A planner should be capable
of finding a sequence of actions that change I into a
state that satisfies G.
Our work was developed based on the FF plan-
ner, more specifically on JavaFF. JavaFF (Coles et al.,
2008b) is a planner and also a planning framework. It
is implemented in Java, based on the source code of
CRIKEY (Coles et al., 2008a), which contains the ba-
sic structure of FF planner. JavaFF is not a full recon-
struction of FF planner, but it preserves the essence of
FF. It has several features necessary in a planner:
• functions and planning heuristics based on FF
planner;
• parser functions for domains and problems de-
scribed in PDDL (Planning Domain Definition
Language) (Fox and Long, 2003);
• implementation of EHC and BFS, which together
form the basis of FF planner;
• examples of domains and planning problems in
PDDL format.
After performing several tests in domains of plan-
ning problems offered by JavaFF by using the default
combination of EHC and BFS, it was possible to iden-
tify some general situations that could hamperthe per-
formance of any search algorithm, such as:
• planning problems with many states that generate
the same successors, demanding a large memory
space;
• states generating many successors, which also re-
quire too much memory space;
• states that generate themselves as successor. If the
planner does not treat repeated states the search
might go into a loop. Therefore, it is necessary
that these states be removed;
• states where the heuristic evaluation demands a
lot of time, usually because they are very far from
the goal. So, if these heuristics need to be re-
calculated every time that a state reappears in the
search, the process tends to be very slow;
• situations in which the search process goes into a
local maximum and gets stuck at dead ends, mak-
ing local search algorithms as EHC fail. In this
case, the strategy of FF and JavaFF is to invoke a
complete algorithm, called BFS, to solve the task
from scratch, thus losing all the previous process-
ing data, which expends more time and memory.
EHC and BFS can be affected by the difficulties
described above. In this work we propose to replace
the use of EHC and BFS with LRTA*, which is a
search algorithm guided by heuristics like EHC and
is as complete as BFS. Moreover, we made some op-
timizations on LRTA*, such as a heap with capacity
to store the states during the search, along with the
pruning of some successors after the expansion of a
state.
4 BACKGROUND
A search tries to determine a sequence of steps to
reach the goal from the initial state of a problem.
Search process can be compared with the process of
building a search tree whose root is the initial state.
The leaf nodes correspond to states waiting to be ex-
panded or states that possess an empty set of succes-
sors. For each step, the search algorithm chooses a
leaf node to expand until it reaches the goal. Search
algorithms generate multiple choices of paths, where
the decision of what path to follow is defined by the
search strategy.
Some algorithms use uninformed search strate-
gies, also called blind search, where there is no infor-
mation about the distance between the current state
SolvingPlanningProblemswithLRTA*
477

and the goal. The most popular uninformed search
algorithms are: breadth-first search, uniform-cost
search, depth-first search, depth-limited search, iter-
ative deepening depth-first search and bidirectional
search.
Informed search strategy, or heuristic search, uses
specific knowledge of the problem to choose the next
state to be expanded. This knowledge can be repre-
sented by a heuristic function that estimates the cost
of the current state to the goal. This estimate indicates
how promising the state is in terms of achieving the
objective. Under this approach, there are two types
of algorithms: off-line and on-line (Furcy, 2004). In
off-line algorithms, the deliberativephase, or planning
phase, is carried out completely before the execution
phase. Therefore, it needs all the time and space nec-
essary to find a solution, and then move onto the exe-
cution. On the other hand, on-line algorithms, known
as real time search algorithms, alternate the deliber-
ative phase and execution during the search process.
They have constraints related to time and information,
i.e., they do not have enough information about the
search space, and after some time they need to return
a solution. In general, on-line algorithms can find so-
lutions faster than off-line algorithms.
A* is an off-line algorithm which combines
uniform-cost search with heuristic search, using the
following evaluation function to determine how good
a state is: f(n) = g(n) + h(n), where g(n) is the amount
spent until reaching the state n and f(n) is the esti-
mated cost to reach the goal from n. This algorithm
had been described firstly by (Hart et al., 1968) and
became known as A. When used with an admissi-
ble heuristic, it reaches the optimal solution, and is
known as A*. However, it is impractical on a large
scale because it keeps in memory all possible paths
during the search process.
LRTA* (Learning Real Time A*) (Korf, 1990)
could be seen as an on-line version of A*. During
the search for a solution, it updates the heuristic val-
ues of the states, forcing it to “learn” whether a path
is good or not. When the solution coming from the
search is executed, more information is obtained from
the environment. In this way, better paths can be ob-
tained later. A basic description of the LRTA* fol-
lows. It begins in the initial state s
initial
and then
transfers to the next step where it moves to the most
promising successor according to its evaluation func-
tion. The search ends when the goal s
goal
is found. At
each iteration, the algorithm updates the estimative of
the distance between the current state s
current
and the
goal, giving more information about the environment
to help the search process.
Algorithm 1: LRTA*(s
initial
,s
goal
).
1: s
current
← s
initial
2: loop
3: s
′
← arg min
s
′′
∈succ(s
current
)
(c(s
current
,s
′′
) + h(s
′′
))
4: if s
current
= s
goal
then
5: h(s
current
) ← h
0
(s
current
)
6: else
7: h(s
current
) ← max(h(s
current
),min
s
′′
∈succ(s
current
)
(c(s
current
,s
′′
) +
h(s
′′
)))
8: end if
9: if s
current
= s
goal
then
10: return
success
11: end if
12: s
current
← s
′
13: end loop
As shown in Algorithm 1, its executioncan be de-
scribed in the following manner: a h value is associ-
ated to each state. The h
0
(s) corresponds to the initial
value of h for a state s. First, the initial state s
initial
is defined as current state s
current
. LRTA* selects a
successor to be the new current state; it is made by
evaluating the minimum sum c(s
current
,s
′′
) + h(s
′′
) of
all adjacent states of s
current
, where ties are broken at
random (line 3). Then, the heuristic value of the cur-
rent state h(s
corrente
) is updated (line 4-8). After that,
it moves to the selected successor (line 12) and a new
iteration starts. This process is repeated until the goal
is reached.
5 HPS-LRTA*
LRTA * is guided by a heuristic evaluation in the
same way as EHC and is as complete as BFS. In
this section we present the algorithm HPS-LRTA*
(Heap&PruningSuccessors-LRTA*), an adaptation of
LRTA*, for generating plans more efficiently and re-
ducing execution time. HPS-LRTA* also allows for
the balancing and storage of states in memory, which
handles the lack of space during the search. Details
concerning these improvements are described below.
• states generated by the algorithm will be stored
in a heap that work as a priority queue, which is
ordered by heuristic values at each state. Thus,
states with higher values will be closer to the root
facilitating their removal if there is not enough
memory. The chance of using states with higher
values of priority again during the search is very
low;
• keeping the states with some structure prevents
the reevaluation of its heuristic value every time
it reappears in the search. In cases where the goal
is far away, this calculation is very slow. Further-
more, storing states ensures that when a heuristic
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
478

of a saved state is updated, it will never be reset.
This is the way LRTA* learns;
• the learning process is one of the greatest ad-
vantages of the algorithm, which is particular to
LRTA*. This is realized by updating the heuristic
value of the current state using the result obtained
from the evaluation function of the best succes-
sor, which allows a more accurate evaluation of
this state if it reappears in the search;
• if a state is generated several times in the search,
just one instance of it remains in the heap, which
saves space;
• when a state generates itself as successor, that suc-
cessor will be pruned, which avoids loops;
• HPS-LRTA* uses the same heuristic function ex-
istent in FF. By considering that such heuristic is
a good function for estimating the number of ac-
tions necessary for achieving the goal, it believes
that states with high heuristic values will not be
promising for the search. Based on this aspect,
and by the fact that there are problems that gener-
ate many successors with the same heuristic val-
ues during the expansion of a state, pruning suc-
cessors with higher heuristics could be a good op-
tion to save space. For this reason, only some of
the successors with lower heuristics will be stored,
while the others will be pruned. Based on experi-
ments, it was observed that a rate of pruning cor-
responding to 0.7 provided the best results;
• another important parameter is the heap capacity
that determines how many states can be stored.
If the search exceeds the heap capacity, its root
(which contains the state with the worst heuristic)
will be removed repeatedly until the capacity re-
turns to normal;
• every state needs to keep a reference to its par-
ent state. This is necessary for the occurrence of
backtracking. The use of backtracking allows the
search process to escape from local maximums
and dead ends, which is something that cannot be
avoided in EHC. Without backtracking, execution
could stop and lose all existing processing data.
Algorithm 2 shows the pseudo-code of the algo-
rithm HPS-LRTA*. The algorithm starts by initial-
izing the heap Q (line 1). The s
current
variable (cur-
rent state) is instantiated to the initial state (line 2)
and added to the heap (line 3). Next, the main loop
starts. Firstly, a balance of the heap is made if neces-
sary. It consists of removing its root repeatedly until
its capacity becomes less than c (maximum capacity
of the heap). This is necessary for allowing enough
memory space during the search (lines 5-7). A test is
Algorithm 2: HPS-LRTA*(s
initial
,s
goal
,r,c).
1: Q ← {}
2: s
current
← s
initial
3: Q.add(s
current
)
4: loop
5: while Q.length() > c do
6: Q.remove()
7: end while
8: if s
current
= s
goal
then
9: return
success
10: end if
11: S ← {arg min
s
′′
∈succ(s
current
)
(c(s
current
,s
′′
) + h(s
′′
))}
12: s
′
← S[random(S.length())]
13: h(s
current
) ← max(h(s
current
),min
s
′′
∈succ(s
current
)
(c(s
current
,s
′′
) +
h(s
′′
)))
14: Q.increaseKey(s
current
,h(s
current
))
15: if s
′
/∈ Q then
16: Q.add(s
′
)
17: end if
18: for i ← 0 to (S.length() × r) do
19: if S[i] /∈ Q then
20: Q.add(S[i])
21: end if
22: end for
23: s
current
← s
′
24: end loop
carried out, which verifies if s
current
reaches the spec-
ified goal. When the goal is achieved, the algorithm
stops the execution and returns success (lines 8-10).
In the next step the expansion phase begins. It
starts by evaluating the minimum sum c(s
current
,s
′′
)+
h(s
′′
) for all successors. These successors make
s
current
their parent, and a set S keeps all successors
that have the lowest h value in this expansion. If a
successor state is exactly the same of scurrent it will
be pruned (line 11). From all the successors at S, one
of them is chosen randomly (line 12).
The heuristic value h(s
current
) of the current state
s
current
is updated with the lowest evaluation of its
successors (line 13). With this new value, the state
must be updated in the heap. This updating might
take this state close to the root if its heuristic gets
worse (line 14). The selected successor is added to
the heap if it is not already there (lines 15-17). The
same happens with a percentage of the successors in
the set S, and the rest are pruned to save space (lines
18-22). The rate of pruning is given by parameter r.
Finally, the move to the selected successor is made
(line 23), and the algorithm realizes another iteration.
6 EXPERIMENTS AND RESULTS
As already mentioned above, our planning system
was built upon JavaFF, a Java implementation of FF.
Essentially, the calls of EHC and BFS were replaced
SolvingPlanningProblemswithLRTA*
479
by a call to HPS-LRTA*. In order to make a compar-
ative analysis between FF and the proposed planner,
both approaches solved planning problems from the
following domains:
• driverlog: warehouse management domain, from
where trucks transport crates and then the crates
must be stacked on pallets at their destinations;
• depots: this domain involves driving trucks,
which deliver packages between locations. The
complication is that the trucks require drivers who
must walk between trucks in order to drive them.
The paths for walking and the roads for driving
form different maps on the locations;
• pipesworld: pipeline domains, where pipes are
used to connect areas.
Usually, each domain has 20 associated problem
instances of increasing size, measured in terms of the
numbers of constants and related goals in each in-
stance (Long and Fox, 2006). In our tests, the driver-
log domain has 20 problems where 01-08 are simple
problems, 09-13 add more location and 14-20 apply
more resources. Depots contains 22 problems which
01-06 are small problems, 07-09 increase the num-
ber of surfaces, 10-12 augment the locations, 13-15
have more surfaces and locations, 16-18 add more
general resources such as trucks and hoists, and 19-
22 increase the problem scale. Pipesworld is a com-
plex domain that contains 50 problems, where even
the first 10 problems are very hard to solve.
Software and hardware configurations include op-
erating system Linux OpenSuse 12.1, processor Intel
Centrino (dual core of 1.4GHz each one), 1.9GiB of
memory and hard disk SATA-82801 of 160GB.
The experiments were carried out by running
JavaFF which combines EHC and BFS, and the al-
gorithm proposed in this paper, HPS-LRTA*. For
each one of these approaches, fifty executions were
realized for each problem of the domains mentioned
above. In order to allow comparative analysis, we
chose only those problems that finished their execu-
tion in at most 30 minutes in both approaches.
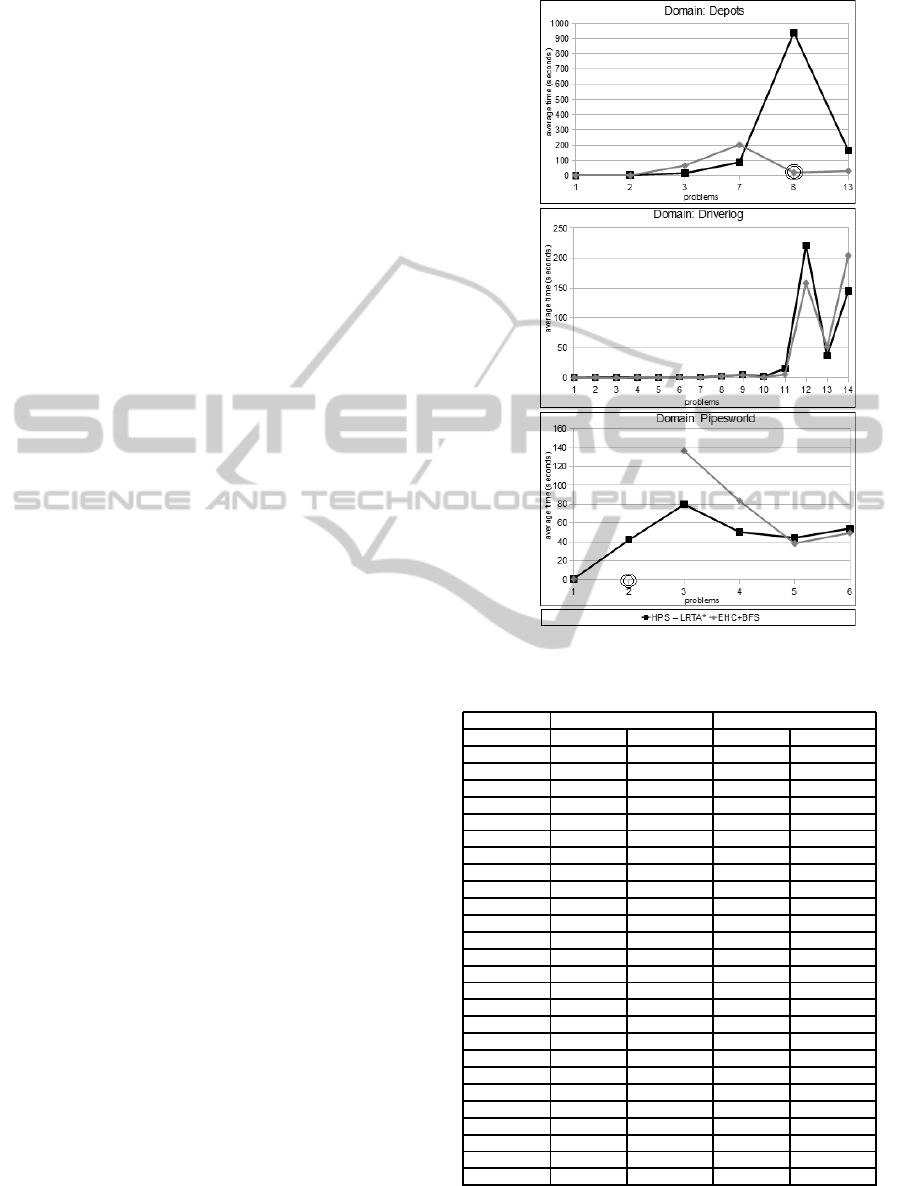
Figure 1 depicts the average runtime for the prob-
lems solved by both approaches.
Table 1 shows the rate of failed executions due to
lack of memory space and their average runtime.
Note that for more difficult problems, the pro-
posed algorithm has a better runtime in most cases.
Moreover, it manages to avoid the lack of memory
space, which might cause the failure of the search.
This failure might happen when FF is employed. For
instance problem 08 in the depots domain and prob-
lem 02 in the pipesworld domain had respectively
86% and 100% of failed executions in the experi-
Figure 1: Average time to successful executions.
Table 1: Rate of failed executions and average time.
Problem Failed Time
EHC + BFS HPS - LRTA* EHC + BFS HPS - LRTA*
Depots 01 0% 0% 0,20 sec. 0,20 sec.
Depots 02 0% 0% 0,50 sec. 1,30 sec.
Depots 03 0% 0% 65,36 sec. 14,93 sec.
Depots 07 8% 0% 202,68 sec. 86,90 sec.
Depots 08 86% 0% 18,41 sec. 940,66 sec.
Depots 13 0% 0% 29,63 sec. 162,81 sec.
Driverlog 01 0% 0% 0,07 sec. 0,25 sec.
Driverlog 02 0% 0% 0,82 sec. 0,69 sec.
Driverlog 03 0% 0% 0,17 sec. 0,54 sec.
Driverlog 04 0% 0% 0,95 sec. 0,83 sec.
Driverlog 05 0% 0% 0,53 sec. 1,07 sec.
Driverlog 06 0% 0% 1,03 sec. 1,23 sec.
Driverlog 07 0% 0% 0,40 sec. 1,24 sec.
Driverlog 08 0% 0% 2,98 sec. 2,67 sec.
Driverlog 09 0% 0% 4,84 sec. 5,25 sec.
Driverlog 10 0% 0% 0,88 sec. 2,55 sec.
Driverlog 11 0% 0% 5,77 sec. 15,31 sec.
Driverlog 12 0% 0% 158,20 sec. 221,46 sec.
Driverlog 13 5% 0% 52,33 sec. 37,02 sec.
Driverlog 14 16% 0% 204,02 sec. 145,39 sec.
Pipesworld 01 0% 0% 0,44 sec. 0,75 sec.
Pipesworld 02 100% 0% ................... 41,96 sec.
Pipesworld 03 0% 0% 136,44 sec. 79,69 sec.
Pipesworld 04 4% 0% 83,52 sec. 50,56 sec.
Pipesworld 05 0% 0% 38,35 sec. 44,25 sec.
Pipesworld 06 4% 0% 49,46 sec. 54,25 sec.
ments. This occurs when EHC reaches a dead end,
and BFS is launched. BFS makes a complete search
ICEIS2013-15thInternationalConferenceonEnterpriseInformationSystems
480

that keeps all the states in memory, which might cause
lack of memory space if the search runs for a long
time.
7 CONCLUSIONS
When concerning simple problems where the initial
state is closer to the goal and few states are generated,
the heuristic proposed by the FF is a useful guide for
search algorithms. Therefore, an agile algorithm such
as EHC can solve problems faster.
However, for more difficult problems in which
many states should be generated and many actions are
required to produce the goal, EHC is inclined to fail
by getting stuck at dead ends. In this case the EHC
execution stops and all the time spent and processing
realized thus far is lost. When this happens, FF starts
a new search from the scratch by using BFS, which
is characterized by a low response time. Also, BFS
needs more space to store the states, which cause it
fail sometimes. In these situations the algorithm HPS-
LRTA* is more efficient, due to the fact that it can es-
cape from a local maximum, avoiding dead ends, and
it also balances the memory space. An improvement
that could be put into practice is to use the concept
of helpful actions in the algorithm, as it is the case
with EHC. Helpful actions filter the most promising
states before the expansion phase, which accelerates
the search process. Also, the authors are planning
to change HPS-LRTA* with respect to the expansion
state. The idea is to generate successors until one
that is better evaluated than the current state, is found.
In doing this we believe that HPS-LRTA* can solve
small problems as fast as EHC.
ACKNOWLEDGEMENTS
This research is supported in part by the Coordination
for the Improvement of Higher Education Personnel
(CAPES), Research Foundation of the State of Minas
Gerais (FAPEMIG) and Faculty of Computing (FA-
COM) from Federal University of Uberlˆandia (UFU).
REFERENCES
Akramifar, S. A. and Ghassem-Sani, G. (2010). Fast for-
ward planning by guided enforced hill climbing. Eng.
Appl. Artif. Intell., 23(8):1327–1339.
Blum, A. and Furst, M. L. (1995). Fast planning through
planning graph analysis. In Proceedings of the 14th in-
ternational joint conference on Artificial intelligence
- Volume 2, IJCAI’95, pages 1636–1642, San Fran-
cisco, CA, USA. Morgan Kaufmann Publishers Inc.
Bonnet, B. and Geffner, H. (1998). Hsp: Heuristic search
planner. Entry at the AIPS-98 Planning Competition,
Pittsburgh.
Coles, A. I., Fox, M., Long, D., and Smith, A. J. (2008a).
Planning with problems requiring temporal coordina-
tion. In Proceedings of the Twenty-Third AAAI Con-
ference on Artificial Intelligence (AAAI 08).
Coles, A. I., Fox, M., Long, D., and Smith, A. J. (2008b).
Teaching forward-chaining planning with javaff. In
Colloquium on AI Education, Twenty-Third AAAI
Conference on Artificial Intelligence.
Fikes, R. and Nilsson, N. J. (1971). Strips: A new approach
to the application of theorem proving to problem solv-
ing. In Cooper, D. C., editor, IJCAI, pages 608–620.
William Kaufmann.
Fox, M. and Long, D. (2003). Pddl2.1: An extension to pddl
for expressing temporal planning domains. Journal of
Artificial Intelligence Research, 20:2003.
Furcy, D. A. (2004). Speeding up the convergence of on-
line heuristic search and scaling up offline heuristic
search. PhD thesis.
Hart, P., Nilsson, N., and Raphael, B. (1968). A Formal Ba-
sis for the Heuristic Determination of Minimum Cost
Paths. IEEE Transactions on Systems Science and Cy-
bernetics, 4:100–107.
Helmert, M. (2006). The fast downward planning system.
Journal of Artificial Intelligence Research, 26:191–
246.
Hoffmann, J. and Nebel, B. (2001). The ff planning system:
Fast plan generation through heuristic search. Journal
of Artificial Intelligence Research, 14:2001.
Korf, R. E. (1990). Real-time heuristic search. Artif. Intell.,
42(2-3):189–211.
Long, D. and Fox, M. (2006). The international planning
competition series and empirical evaluation of ai plan-
ning systems. In Paquete, L., Chiarandini, M., and
Basso, D., editors, Proceedings of Workshop on Em-
pirical Methods for the Analysis of Algorithm.
Rames Basilio Junior, R. and Lopes, C. (2012). An ap-
proach to action planning based on simulated anneal-
ing. In Systems, Man, and Cybernetics (SMC), 2012
IEEE International Conference on, pages 2085 –2090.
Richter, S. and Westphal, M. (2010). The lama planner:
Guiding cost-based anytime planning with landmarks.
Russell, S. J. and Norvig, P. (2009). Artificial Intelligence:
A Modern Approach. Prentice Hall, 3rd edition.
Stern, R., Puzis, R., and Felner, A. (2011). Potential search:
A bounded-cost search algorithm. In ICAPS.
Xie, F., Nakhost, H., and M¨uller, M. (2012). Planning via
random walk-driven local search. In ICAPS.
SolvingPlanningProblemswithLRTA*
481
