
Phase-frequency Domain Model of Costas Loop
with Mixer Discriminator
N. V. Kuznetsov
1,2
, G. A. Leonov
2
, P. Neittaanm¨aki
1
, S. M. Seledzhi
2
,
M. V. Yuldashev
1,2
and R. V. Yuldashev
1,2
1
Dept. of Mathematical Information Technology, University of Jyv¨askyl¨a,
P.O. Box 35 (Agora), Jyv¨askyl¨a, FIN-40014, Finland
2
Faculty of Mathematics and Mechanics, Saint-Petersburg State University,
Universitetski pr. 28, Saint-Petersburg, 198504, Russia
Keywords:
Costas Loop, Phase-locked Loop, Phase Detector Characteristic, Mathematical Model, Nonlinear Analysis.
Abstract:
Problem of rigorous mathematical analysis of classical Costas Loop for non-sinusoidal signals is considered.
The analytical method for phase detector characteristics computation is proposed and new classes of phase
detector characteristics are computed for the first time. Effective methods for nonlinear analysis of Costas
Loop are discussed.
1 INTRODUCTION
The Costas loop is a classical phase-locked loop
(PLL) based circuit for carrier recovery (Best, 2007;
Costas, 1956; Djordjevic et al., 1998; Waters,
1982). Nowadays various modifications of Costas
loop circuit are used in many communication devices,
e.g. Global Positioning Systems (GPS) (Kaplan and
Hegarty, 2006; Nowsheen et al., 2010; Hasegawa
et al., 2001).
Although PLL-based circuits are essentially a
nonlinear control systems, in modern engineering lit-
erature, devoted to the analysis of PLL-based cir-
cuits, the main direction is the use of simplified lin-
ear models, the methods of linear analysis, empirical
rules, and numerical simulation (see a plenary lecture
of D. Abramovich at American Control Conference
2002 (Abramovitch, 2002)). While the linearization
and analysis of linearized models of control systems
may lead to incorrect conclusions
1
, the attempts to
justify the reliability of conclusions, based on the ap-
plication of such simplified approaches, are quite rare
(see, e.g., (Suarez and Quere, 2003; Margaris, 2004;
1
see, e.g. counterexamples to filter hypothesis and to
Aizerman’s and Kalman’s conjectures on absolute stabil-
ity (Leonov and Kuznetsov, 2011; Leonov et al., 2011b;
Kuznetsov et al., 2011a; Bragin et al., 2011; Leonov
and Kuznetsov, 2013) and Perron effects of Lyapunov
exponents sign inversions for time varying linearizations
(Leonov and Kuznetsov, 2007) etc.
Feely, 2007; Banerjee and Sarkar, 2008; Feely et al.,
2012; Suarez et al., 2012)). Rigorous nonlinear analy-
sis of PLL-based circuit models is often very difficult
task, so for analysis of nonlinear PLL models, numer-
ical simulation is widely used (Troedsson, 2009; Best,
2007; Bouaricha et al., 2012). However for high-
frequency signals, complete numerical simulation of
physical model of PLL-based circuit in signals/time
space, described by nonlinear non-autonomous sys-
tem of differential equations, is highly complicated
(Abramovitch, 2008a; Abramovitch, 2008b) since it
is necessary to simultaneously observe “very fast time
scale of the input signals” and “slow time scale of
signal’s phases”. Here a relatively small discretiza-
tion step in numerical procedure does not allow one to
consider transition processes for high-frequency sig-
nals in a reasonable time.
To overcome these difficulties, it is possible to
construct mathematical model of PLL-based circuit
in phase-frequency/time space, described by nonlin-
ear dynamical system of differential equations. In
this case only slow time scale of signal’s phases is
investigated. That, in turn, requires (Leonov et al.,
2012b) the computation of phase detector character-
istic (a nonlinear element used to match reference
and controllable signals), which depends on wave-
forms of considered signals (Kuznetsov et al., 2011c;
Kuznetsov et al., 2011b; Kuznetsov et al., 2010a).
However, the use of results of this mathematical
model analysis for conclusions, concerning the be-
427
V. Kuznetsov N., A. Leonov G., Neittaanmaki P., M. Seledzhi S., V. Yuldashev M. and V. Yuldashev R..
Phase-frequency Domain Model of Costas Loop with Mixer Discriminator.
DOI: 10.5220/0004479104270433
In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2013), pages 427-433
ISBN: 978-989-8565-70-9
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

havior of considered physical model, requires rigor-
ous justification (Leonov et al., 2011b; Leonov et al.,
2012b).
All in all discovery of hidden oscillations
2
in
nonlinear dynamical models of PLL (Leonov and
Kuznetsov, 2013) shows that for investigation of pos-
sible behavior of nonlinear systems, simple simula-
tion is an unreliable tool and can lead to wrong con-
clusions. For numerical computation of possible limit
solutions in a dynamic system, all initial conditions
need to be evaluated, and in a non-autonomous sys-
tems with input, in addition, all possible inputs need
to be considered. Here to get reliable results of sim-
ulations one need to verify analytically a condition of
uniqueness of limit solution (i.e. convergent prop-
erty of systems (van den Berg et al., 2006)) or to
apply special analytical-numerical procedures, which
allow to compute hidden oscillations (Leonov and
Kuznetsov, 2011; Bragin et al., 2011; Leonov et al.,
2011a; Leonov et al., 2012a).
In this paper effective approaches to rigorous
nonlinear analysis of classical analog Costas loop
are discussed. For computation of phase-detector
characteristics, effective analytical method is demon-
strated. For various non-sinusoidal waveforms of
high-frequency signals, new classes of phase-detector
characteristics are obtained, and dynamical model of
Costas loop is constructed.
2 DESCRIPTION
OF THE COSTAS LOOP
IN THE SIGNAL SPACE
Consider the Costas loop with harmonic carrier
(Fig. 1). Here input signal is Binary Phase Shift Key-
ing (BPSK) signal, which is a product of transferred
data m(t) = ±1 and harmonic carrier sin(ωt) with
high frequency ω. Input signal is multiplied (block
N
) with the output of voltage-controlled oscillator
(VCO) in the upper branch (I branch)
I =
1
2
m(t)cos(0) − m(t)cos(2ωt)
.
(1)
2
From a computational point of view, in nonlinear dy-
namical systems, attractors can be regarded as self-excited
and hidden attractors (Kuznetsov et al., 2010b; Leonov and
Kuznetsov, 2011; Leonov et al., 2011a; Bragin et al., 2011;
Leonov et al., 2012a; Leonov and Kuznetsov, 2013). Self-
excited attractors can be localized numerically by a stan-
dard computational procedure, in which after a transient
process a trajectory, started from a point of unstable man-
ifold in a neighborhood of equilibrium, reaches a state of
oscillation and therefore one can easily identify it. In con-
trast, for a hidden attractor, its basin of attraction does not
intersect with small neighborhoods of equilibria.
1
2
(
1
2
(
)
)
VCO Filter
=
=I
=Q
Filter
Filter
m(t)
Figure 1: Costas loop: m(t) is a transferred data (±1);m(t)
sin(ωt) is an input signal; ω is a frequency of oscillators.
Filtration (blocks Filter) of high frequency compo-
nent cos(2ωt) allows to get demodulated data m(t).
In the lower branch (Q branch) the phase of VCO sig-
nal is shifted by −
π
2
Q =
1
2
m(t)sin(0) − m(t)sin(2ωt)
.
(2)
This signal after filtration of high frequency compo-
nent sin(2ωt) can be used to detect a lock state of the
loop. Then both branches are multiplied together and
next low-pass filter forms control signal for VCO in
order to adjust its frequency to the frequency of the
carrier.
Here to avoid these non-rigorous arguments, and
to consider non-sinusoidal (see applications, e.g., in
(Henning, 1981; Wang and Emura, 1998; Sutterlin
and Downey, 1999; Wang and Emura, 2001; Chang
and Chen, 2008; Sarkar and Sengupta, 2010)) mathe-
matical properties of high-frequency oscillations will
be considered.
3 COMPUTATION
OF PHASE DETECTOR
CHARACTERISTIC
Since two arm filters are used for data demodulation
and can be applied apart from the loop (see e.g. (Ka-
plan and Hegarty, 2006)), for investigation of tran-
sient processes one can consider simplified block dia-
gram of Costas loop in Fig. 2. Here signals f
1,2
(t) =
Figure 2: Multiplier and filter.
f
1,2
(θ
1,2
(t)) with θ
1,2
(t) as phases are carrier and out-
put of VCO. Suppose that the waveforms f
p
(θ) of
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
428

signals are bounded 2π-periodic piecewise differen-
tiable functions
3
(this is true for the most considered
waveforms). Consider Fourier series representation
of such functions:
f
p
(θ) =
∞
∑
i=1
a
p
i
cos(iθ) + b
p
i
sin(iθ)
,
a
p
i
=
1
π
π
R
−π
f
p
(θ)cos(iθ)dθ,
b
p
i
=
1
π
π
R
−π
f
p
(θ)sin(iθ)dθ, p = 1, 2,
Assume that relation between the input ξ(t) and
the output σ(t) of Filter has the form:
σ(t) = α
0
(t) +
Z
t
0
γ(t − τ)ξ(τ)dτ, (3)
where γ(t) is an impulse response function of filter
and α
0
(t) is an exponentially damped function de-
pending on the initial data of filter at moment t = 0.
By assumption, γ(t) is a differentiable function with
bounded derivative (this is true for the most consid-
ered liner filters (Thede, 2005)).
A high-frequency property of signals can be refor-
mulated in the following condition.
Frequencies ω
p
(t) of signals can be defined
(Leonov, 2008) as follows θ
1,2
(t) = ω
1,2
(t)t + ψ
1,2
.
Consider a large fixed time interval [0, T], which can
be partitioned into small intervals of the form
[τ, τ+ δ], τ ∈ [0, T],
where the following relations
|γ(t) − γ(τ)| ≤ Cδ, |ω
p
(t) − ω
p
(τ)| ≤ Cδ,
∀t ∈ [τ, τ + δ], ∀ τ ∈ [0, T],
(4)
|ω
1
(τ) − ω
2
(τ)| ≤ C
1
, ∀ τ ∈ [0, T], (5)
ω
p
(t) ≥ ω
min
, ∀t ∈ [0, T], p = 1, 2 (6)
are satisfied.
Suppose that δ is sufficiently small as compared
with the fixed numbers T,C,C
1
and ω
min
is suffi-
ciently large as compared with the number δ : ω
−1
min
=
O(δ
2
).
The latter means that on small intervals [τ, τ + δ]
the functions γ(t) and ω
1,2
(t) are “almost constant”
and the functions f
1,2
(t) are rapidly oscillating. Ob-
viously, such a condition occurs for high-frequency
oscillations.
Consider equivalent block diagram of Costas loop
(Fig. 3) in phase-frequency space. Here θ
1,2
(t) are
phases of oscillations f
1,2
θ
1,2
(t)
, PD is a nonlin-
ear block with the characteristic ϕ(θ) (being called a
3
The functions with a finite number of jump discontinu-
ity points differentiable on their continuity intervals.
Figure 3: Phase detector and filter.
Phase Detector or discriminator). The phases θ
1,2
(t)
are the inputs of PD block and the output is the func-
tion ϕ(θ
1
(t) − θ
2
(t)). A shape of phase detector char-
acteristic is based on a shape of input signals.
In the both diagrams (Figs. 2 and 3) the filters are
the same with the same impulse transient function γ(t)
and the same initial data. The filters outputs are the
functions g(t) and G(t), respectively. By (3) one can
obtain g(t) and G(t):
g(t) =α
0
(t) +
Z
t
0
γ(t − τ) f
1
θ
1
(τ)
f
2
θ
2
(τ)
f
1
θ
1
(τ)
f
2
θ
2
(τ)
dτ,
G(t)=α
0
(t) +
Z
t
0
γ(t − τ)ϕ
θ
1
(τ) − θ
2
(τ)
dτ.
(7)
Using the approaches outlined in (Leonov, 2008;
Kuznetsov et al., 2010a; Kuznetsov et al., 2011c;
Kuznetsov et al., 2012), the following result can be
proved.
Theorem 1. If conditions (4)–(6) are satisfied (high-
frequency property) and
ϕ(θ) =
A
1
0
A
2
0
4
+
1
2
∞
∑
l=1
(A
1
l
A
2
l
+ B
1
l
B
2
l
)cos(lθ)+
(A
1
l
B
2
l
− B
1
l
A
2
l
)sin(lθ)
,
(8)
where
A
1
0
=
a
1
0
a
1
0
2
+
∞
∑
m=1
(a
1
m
a
1
m
+ b
1
m
b
1
m
),
A
1
k
=
a
1
0
a
1
k
2
+
1
2
∞
∑
m=1
[a
1
m
(a
1
m+k
+a
1
m−k
)+b
1
m
(b
1
m+k
+b
1
m−k
)],
B
1
k
=
a
1
0
b
1
k
2
+
1
2
∞
∑
m=1
[a
1
m
(b
1
m+k
−b
1
m−k
)−b
1
m
(a
1
m+k
−a
1
m−k
)],
A
2
0
=
a
2
0
a
2
0
2
+
∞
∑
m=1
(α
2
m
α
2
m
+ β
2
m
β
2
m
),
A
2
k
=
a
2
0
α
2
k
2
+
1
2
∞
∑
m=1
[α
2
m
(α
2
m+k
+α
2
m−k
)+β
2
m
(β
2
m+k
+β
2
m−k
)],
B
2
k
=
a
2
0
β
2
k
2
+
1
2
∞
∑
m=1
[α
2
m
(β
2
m+k
−β
2
m−k
−β
2
m
(α
2
m+k
−α
2
m−k
)],
(9)
Phase-frequencyDomainModelofCostasLoopwithMixerDiscriminator
429

and
α
2
k
=
a
2
k
, k = 4p,
b
2
k
, k = 4p+ 1,
−a
2
k
, k = 4p+ 2,
−b
2
k
, k = 4p+ 3,
β
2
k
=
b
2
k
, k = 4p,
−a
2
k
, k = 4p+ 1,
−b
2
k
, k = 4p+ 2,
a
2
k
, k = 4p+ 3,
(10)
then for the same initial data of filter the following
relation
G(t) − g(t) = O(δ), ∀t ∈ [0, T] (11)
is valid.
3.1 Proof of Theorem
Let t ∈ [0, T]. Consider the difference
g(t) − G(t) =
t
Z
0
γ(t − s)
f
1
θ
1
(s)
f
2
θ
2
(s)
f
1
θ
1
(s)
f
2
θ
2
(s) −
π
2
−
− ϕ
θ
1
(s) − θ
2
(s)
ds.
(12)
Denote by m ∈ N ∪{0} a natural number such that
t ∈ [mδ, (m+ 1)δ]. Then
m <
T
δ
+ 1. (13)
The function γ(t) is continuous and, therefore, it is
bounded on [0, T]. In addition, f
1
(θ), f
2
(θ), ϕ
θ
are
bounded on R. Then
(m+1)δ
Z
t
γ(t − s) f
1
θ
1
(s)
f
2
θ
2
(s)
f
1
θ
1
(s)
f
2
θ
2
(s) −
π
2
ds = O(δ),
(m+1)δ
Z
t
γ(t − s)ϕ
θ
1
(s) − θ
2
(s)
ds = O(δ).
(14)
So (12) can be rewritten as
g(t) − G(t) =
m
∑
k=0
Z
[kδ,(k+1)δ]
γ(t − s)
f
1
θ
1
(s)
f
2
θ
2
(s)
f
1
θ
1
(s)
f
2
θ
2
(s) −
π
2
−
− ϕ
θ
1
(s) − θ
2
(s)
ds+ O(δ).
(15)
Since (4), it follows that on any interval
[kδ, (k+ 1)δ] (16)
one obtains
γ(t − s) = γ(t − kδ) + O(δ),
t > s, s ∈ [kδ, (k + 1)δ].
(17)
Here s ∈ [kδ, (k + 1)δ] and O(δ) is independent on
k. Then by (15), (17) and the boundedness of
f
1
(θ), f
2
(θ), ϕ
θ
one gets
g(t) − G(t) =
m
∑
k=0
γ(t − kδ)
Z
[kδ,(k+1)δ]
f
1
θ
1
(s)
f
2
θ
2
(s)
f
1
θ
1
(s)
f
2
θ
2
(s) −
π
2
−
− ϕ
θ
1
(s) − θ
2
(s)
ds+ O(δ).
(18)
Denote
θ
p
k
(s) = θ
p
(kδ) + ω
p
(kδ)(s− kδ), p = 1, 2.
(19)
Now, by (5) with s ∈ [kδ, (k+ 1)δ]
θ
p
(s) = θ
p
k
(s) + O(δ). (20)
Since ϕ
θ
is bounded and continuous on R, one ob-
tains
Z
[kδ,(k+1)δ]
ϕ
θ
1
(s) − θ
2
(s)
− ϕ
θ
1
k
(s) − θ
2
k
(s)
ds =
= O(δ
2
),
(21)
The function f
2
(θ) is smooth while the function
f
1
(θ) is piecewise differentiable and bounded. If
f
1
(θ) is also continuous on R, then
Z
[kδ,(k+1)δ]
f
1
(θ
1
(s)) f
2
(θ
2
(s)) f
1
θ
1
(s)
f
2
θ
2
(s) −
π
2
ds =
=
Z
[kδ,(k+1)δ]
f
1
θ
1
k
(s)
f
2
θ
2
k
(s)
f
1
θ
1
k
(s)
f
2
θ
2
k
(s) −
π
2
ds+ O(δ
2
).
(22)
Considering sets (22) outside of sufficiently small
neighbourhoods of discontinuity points and using
(4)–(6), the proof of theorem is completed.
3.2 Example
Consider triangular and sawtooth signals (Fig. 4)
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
430

-1
-0.5
0
0.5
1
1.5
2
0 2 4 6 8 10 12 14
-1
-0.5
0
0.5
1
1.5
2
0 2 4 6 8 10 12 14
Figure 4: Triangular and sawtooth signal waveforms.
f
1
(θ) =
8
π
2
∞
∑
n=1
1
(2n− 1)
2
cos
(2n− 1)θ
f
2
(θ) = −
2
π
∞
∑
n=1
1
n
sin
nθ
.
Then by Theorem 1 one gets the following character-
istics (Fig. 5)
ϕ(θ) = −
1
72
+
2
π
2
sin(2θ)+
+
2
π
2
∞
∑
l=1
1
π
2
l
4
cos(2lθ), l = 2p,
1
πl
3
sin(2lθ), l = 2p + 1, p ∈ N
-0.1
-0.05
0
0.05
0.1
0 2 4 6 8 10 12 14
Figure 5: PD characteristics.
4 COSTAS EQUATIONS
IN PHASE-FREQUENCY SPACE
From Theorem 1 it follows that physical model of
classical Costas loop in signals space (Fig. 1) can be
asymptotically changed (for high-frequency genera-
tors) to mathematical model in phase-frequency space
(Fig. 6).
VCO
Figure 6: Phase-locked loop with phase detector.
Here PD is a phase detector with corresponding
characteristics. Thus, on basis of asymptotic analy-
sis of high-frequency oscillations, characteristics of
phase detector can be computed.
The following remark is useful for derivation of
differential equations of PLL.
Consider a quantity
˙
θ
p
(t) = ω
p
(t) +
˙
ω
p
(t)t, p = 1, 2.
For correctly designed PLL such that it possesses the
property of global stability, there occurs exponential
damping of
˙
ω
j
(t):
|
˙
ω
p
(t)| ≤ Ce
−αt
, p = 1, 2.
Here C and α are certain positive numbers indepen-
dent of t. Therefore,
˙
ω
p
(t)t is, as a rule, sufficiently
small as compared with the number ω
min
(see con-
ditions (5)– (6)). From the above one can conclude
that the following approximate relation
˙
θ
p
(t) ≈ ω
p
(t)
is valid. In deriving the differential equations of this
PLL, it can be used a block diagram in Fig. 6 and the
following relation
˙
θ
p
(t) = ω
p
(t), p = 1, 2. (23)
Note that usually the control law of tunable oscil-
lators is considered linear:
˙
θ
2
(t) = ω
2
(0) + LG(t). (24)
Here ω
2
is a free-running frequency of tunable oscil-
lator, L is a certain number, and G(t) is a control sig-
nal, which is a filter output (Fig. 3). Thus, the equa-
tion of Costas loop is as follows
˙
θ
2
(t) = ω
2
(0)+
+ L
α
0
(t) +
t
Z
0
γ(t − τ)ϕ
θ
1
(τ) − θ
2
(τ)
dτ
.
(25)
Assuming that the master oscillator is such that
˙
θ
1
(t) ≡ ω
1
(0), one can obtain the following equation
for Costas loop
θ
1
(t)−θ
2
(t)
′
+
+L
α
0
(t) +
t
R
0
γ(t − τ)ϕ
θ
1
(τ)−θ
2
(τ)
dτ
=
= ω
1
(0) − ω
2
(0).
(26)
This is an equation of classical PLL.
The above theoretical results is justified by sim-
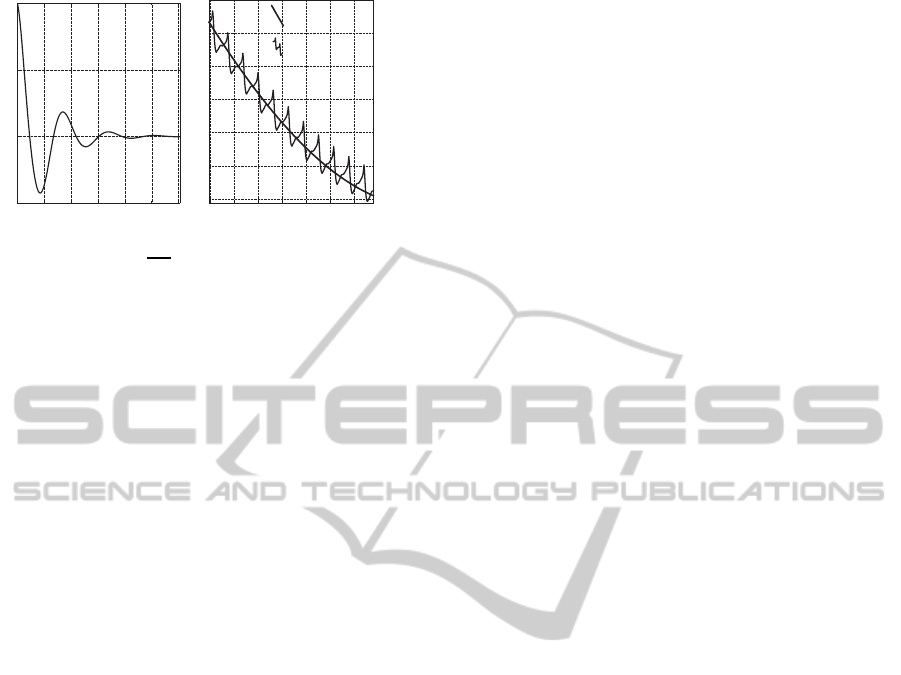
ulation of Costas loop model in phase-frequency
space and signal space (Fig. 7). Unlike the filter
output for mathematical model in phase-frequency
space, the output of filter for physical model in sig-
nals space contains additional high-frequency oscil-
lations. These high-frequency oscillations interfere
with qualitative analysis and efficient simulation of
Costas loop.
The analysis of mathematical model of Costas
loop is based on the theory of phase synchroniza-
tion. This theory was developed in the second half
of the last century on the basis of three applied the-
ories: the theory of synchronous and induction elec-
trical motors, the theory of auto-synchronization of
unbalanced rotors, and the theory of phase-locked
Phase-frequencyDomainModelofCostasLoopwithMixerDiscriminator
431
-0.5
0
-1
-1.5
2 4 6 8 10 12
time
lter output
-0.9
-1
-1.1
-1.2
-1.3
-1.4
0.8 0.9 1 1.1 1.2 1.3 1.4
time
phase/frequency
space
signal space
Figure 7: ω
2
(0) = 101 Hz, ω
1
(0) = 100 Hz, L = 30, fil-
ter transfer functions
1
s+1
, triangular (input) and sawtooth
(VCO) waveforms.
loops. Modification of direct Lyapunov method with
the construction of periodic Lyapunov-like functions,
the method of positively invariant cone grids, and the
method of nonlocal reduction turned out to be most
effective (Leonov et al., 1996; Leonov, 2006; Leonov
et al., 2009). The latter method, which combines
the elements of direct Lyapunov method and bifur-
cation theory, allows one to extend the classical re-
sults of F. Tricomi (Tricomi, 1993) and his proge-
nies (Kudrewicz and Wasowicz, 2007) to the multi-
dimensional dynamical systems.
5 CONCLUSIONS
The approach, proposed in this paper, allows one to
compute analytically phase-detector characteristics of
costas loop in the case of non-sinusoidal signal wave-
forms and to proceed from analysis of classical Costas
loop in space of signals to analysis and simulation in
space of signals phases and, ultimately, to simulate
effectively classical Costas loop circuits.
ACKNOWLEDGEMENTS
This work was supported by Academy of Finland,
Ministry of Education and Science, Russian Founda-
tion for Basic Research, and Saint-Petersburg State
University (Russia).
REFERENCES
Abramovitch, D. (2002). Phase-locked loops: A control
centric tutorial. In Proceedings of the American Con-
trol Conference, volume 1, pages 1–15.
Abramovitch, D. (2008a). Efficient and flexible simula-
tion of phase locked loops, part I: simulator design.
In American Control Conference, pages 4672–4677,
Seattle, WA.
Abramovitch, D. (2008b). Efficient and flexible simulation
of phase locked loops, part II: post processing and a
design example. In American Control Conference,
pages 4678–4683, Seattle, WA.
Banerjee, T. and Sarkar, B. (2008). Chaos and bifurcation in
a third-order digital phase-locked loop. International
Journal of Electronics and Communications, (62):86–
91.
Best, R. E. (2007). Phase-Lock Loops: Design, Simulation
and Application. McGraw-Hill.
Bouaricha, A. et al. (2012). Hybrid time and frequency
solution for PLL sub-block simulation. US Patent
8,209,154.
Bragin, V. O., Vagaitsev, V. I., Kuznetsov, N. V., and
Leonov, G. A. (2011). Algorithms for finding hid-
den oscillations in nonlinear systems. The Aizerman
and Kalman conjectures and Chua’s circuits. Jour-
nal of Computer and Systems Sciences International,
50(4):511–543. 10.1134/S106423071104006X.
Chang, G. and Chen, C. (2008). A comparative study of
voltage flicker envelope estimation methods. In Power
and Energy Society General Meeting - Conversion
and Delivery of Electrical Energy in the 21st Century,
pages 1–6.
Costas, J. (1956). Synchoronous communications. In Proc.
IRE, volume 44, pages 1713–1718.
Djordjevic, I. B., Stefanovic, M. C., Ilic, S. S., and Djord-
jevic, G. T. (1998). An example of a hybrid system:
Coherent optical system with costas loop in receiver-
system for transmission in baseband. J. Lightwave
Technol., 16(2):177.
Feely, O. (2007). Nonlinear dynamics of discrete-time cir-
cuits: A survey. International Journal of Circuit The-
ory and Applications, (35):515–531.
Feely, O., Curran, P. F., and Bi, C. (2012). Dynamics of
charge-pump phase-locked loops. International Jour-
nal of Circuit Theory and Applications. 10.1002/cta.
Hasegawa, K., Kanetsuna, H., and Wakamori, M. (2001).
GPS positioning method and GPS reception appara-
tus. EP1092987 A2.
Henning, F. H. (1981). Nonsinusoidal Waves for Radar and
Radio Communication. Academic Pr, first edition.
Kaplan, E. and Hegarty, C. (2006). Understanding GPS:
Principles and Applications. Artech House.
Kudrewicz, J. and Wasowicz, S. (2007). Equations of
Phase-Locked Loops: Dynamics on the Circle, Torus
and Cylinder, volume 59 of A. World Scientific.
Kuznetsov, N. V., Leonov, G. A., Neittaanm¨aki, P.,
Seledzhi, S. M., Yuldashev, M. V., and Yulda-
shev, R. V. (2010a). Nonlinear analysis of phase-
locked loop. IFAC Proceedings Volumes (IFAC-
PapersOnline), 4(1):34–38. 10.3182/20100826-3-
TR-4016.00010.
Kuznetsov, N. V., Leonov, G. A., and Seledzhi,
S. M. (2011a). Hidden oscillations in nonlin-
ear control systems. IFAC Proceedings Vol-
umes (IFAC-PapersOnline), 18(1):2506–2510.
10.3182/20110828-6-IT-1002.03316.
ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics
432

Kuznetsov, N. V., Leonov, G. A., and Vagaitsev, V. I.
(2010b). Analytical-numerical method for attractor
localization of generalized Chua’s system. IFAC Pro-
ceedings Volumes (IFAC-PapersOnline), 4(1):29–33.
10.3182/20100826-3-TR-4016.00009.
Kuznetsov, N. V., Leonov, G. A., Yuldashev, M. V., and Yul-
dashev, R. V. (2011b). Analytical methods for com-
putation of phase-detector characteristics and PLL de-
sign. In ISSCS 2011 - International Symposium on
Signals, Circuits and Systems, Proceedings, pages 7–
10. 10.1109/ISSCS.2011.5978639.
Kuznetsov, N. V., Leonov, G. A., Yuldashev, M. V.,
and Yuldashev, R. V. (2012). Nonlinear analysis
of Costas loop circuit. ICINCO 2012 - Proceed-
ings of the 9th International Conference on Informat-
ics in Control, Automation and Robotics, 1:557–560.
10.5220/0003976705570560.
Kuznetsov, N. V., Neittaanm¨aki, P., Leonov, G. A.,
Seledzhi, S. M., Yuldashev, M. V., and Yulda-
shev, R. V. (2011c). High-frequency analysis of
phase-locked loop and phase detector characteris-
tic computation. ICINCO 2011 - Proceedings
of the 8th International Conference on Informatics
in Control, Automation and Robotics, 1:272–278.
10.5220/0003522502720278.
Leonov, G. A. (2006). Families of transverse curves
for two-dimensional systems of differential equations.
Vestnik St.Petersburg University, (4):48–78.
Leonov, G. A. (2008). Computation of phase detector char-
acteristics in phase-locked loops for clock synchro-
nization. Doklady Mathematics, 78(1):643–645.
Leonov, G. A. and Kuznetsov, N. V. (2007). Time-varying
linearization and the Perron effects. International
Journal of Bifurcation and Chaos, 17(4):1079–1107.
10.1142/S0218127407017732.
Leonov, G. A. and Kuznetsov, N. V. (2011). Analytical-
numerical methods for investigation of hidden os-
cillations in nonlinear control systems. IFAC Pro-
ceedings Volumes (IFAC-PapersOnline), 18(1):2494–
2505. 10.3182/20110828-6-IT-1002.03315.
Leonov, G. A. and Kuznetsov, N. V. (2013). Hidden attrac-
tors in dynamical systems. From hidden oscillations
in Hilbert-Kolmogorov, Aizerman, and Kalman prob-
lems to hidden chaotic attractors in Chua circuits. In-
ternational Journal of Bifurcation and Chaos, 23(1).
10.1142/S0218127413300024, art. no. 1330002.
Leonov, G. A., Kuznetsov, N. V., and Seledzhi, S. M.
(2009). Automation control - Theory and Practice,
chapter Nonlinear Analysis and Design of Phase-
Locked Loops, pages 89–114. In-Tech.
Leonov, G. A., Kuznetsov, N. V., and Vagaitsev,
V. I. (2011a). Localization of hidden Chua’s at-
tractors. Physics Letters A, 375(23):2230–2233.
10.1016/j.physleta.2011.04.037.
Leonov, G. A., Kuznetsov, N. V., and Vagaitsev, V. I.
(2012a). Hidden attractor in smooth Chua systems.
Physica D: Nonlinear Phenomena, 241(18):1482–
1486. 10.1016/j.physd.2012.05.016.
Leonov, G. A., Kuznetsov, N. V., Yuldahsev, M. V.,
and Yuldashev, R. V. (2011b). Computation
of phase detector characteristics in synchronization
systems. Doklady Mathematics, 84(1):586–590.
10.1134/S1064562411040223.
Leonov, G. A., Kuznetsov, N. V., Yuldahsev, M. V., and Yul-
dashev, R. V. (2012b). Analytical method for compu-
tation of phase-detector characteristic. IEEE Trans-
actions on Circuits and Systems – II: Express Briefs,
59(10):633–647. 10.1109/TCSII.2012.2213362.
Leonov, G. A., Ponomarenko, D. V., and Smirnova, V. B.
(1996). Frequency-Domain Methods for Nonlinear
Analysis. Theory and Applications. World Scientific,
Singapore.
Margaris, W. (2004). Theory of the Non-Linear Analog
Phase Locked Loop. Springer Verlag, New Jersey.
Nowsheen, N., Benson, C., and Frater, M. (2010). Design of
a high frequency fpga acoustic modem for underwa-
ter communication. In OCEANS 2010 IEEE-Sydney,
pages 1–6. IEEE.
Sarkar, A. and Sengupta, S. (2010). Second-degree digital
differentiator-based power system frequency estima-
tion under non-sinusoidal conditions. IET Sci. Meas.
Technol., 4(2):105–114.
Suarez, A., Fernandez, E., Ramirez, F., and Sancho, S.
(2012). Stability and bifurcation analysis of self-
oscillating quasi-periodic regimes. IEEE transactions
on microwave theory and techniques, 60(3):528–541.
Suarez, A. and Quere, R. (2003). Stability Analysis of Non-
linear Microwave Circuits. Artech House, New Jer-
sey.
Sutterlin, P. and Downey, W. (1999). A power line com-
munication tutorial - challenges and technologies. In
Technical Report. Echelon Corporation.
Thede, L. (2005). Practical analog and digital filter design.
Artech House.
Tricomi, F. (1993). Integrazione di differeziale presentasi in
electrotechnica. Annali della Roma Schuola Normale
Superiore de Pisa, 2(2):1–20.
Troedsson, N. (2009). Method and simulator for generating
phase noise in system with phase-locked loop. US
Patent App. 12/371,828.
van den Berg, R., Pogromsky, A., and Rooda, K.
(2006). Convergent systems design: Anti-windup for
marginally stable plants. In 45th IEEE Conference on
Decision and Control, pages 5441–5446. Optical So-
ciety of America.
Wang, L. and Emura, T. (1998). A high-precision position-
ing servo-controller using non-sinusoidal two-phase
type PLL. In UK Mechatronics Forum International
Conference, pages 103–108. Elsevier Science Ltd.
Wang, L. and Emura, T. (2001). Servomechanism using
traction drive. JSME International Journal Series C,
44(1):171–179.
Waters, G. W. (1982). Costas loop QPSK demodulator. US
Patent 4,344,178.
Phase-frequencyDomainModelofCostasLoopwithMixerDiscriminator
433
