Efficient Characteristic 3 Galois Field Operations
for Elliptic Curve Cryptographic Applications
Vinay S. Iyengar
Oregon Episcopal School, Portland, Oregon, U.S.A.
Keywords: Public-Key Cryptography, Elliptic Curves, Characteristic 3 Galois Field Theory, Performance Optimization.
Abstract: Galois fields of characteristic 3, where the number of field elements is a power of 3, have a distinctive
application in building high-security elliptic curve cryptosystems. However, they are not typically used
because of their relative inefficiency in computing polynomial operations when compared to conventional
prime or binary Galois fields. The purpose of this research was to design and implement characteristic 3
Galois field arithmetic algorithms with greater overall efficiency than those presented in current literature,
and to evaluate their applicability to elliptic curve cryptography. The algorithms designed were tested in a
C++ program and using a mapping of field element logarithms, were able to simplify the operations of
polynomial multiplication, division, cubing, and modular reduction to that of basic integer operations. They
thus significantly outperformed the best characteristic 3 algorithms presented in literature and showed a
distinct applicability to elliptic curve cryptosystems. In conclusion, this research presents a novel method of
optimizing the performance of characteristic 3 Galois fields and has major implications for the field of
elliptic curve cryptography.
1 INTRODUCTION
Galois fields are one of the most important concepts
in abstract algebra and have a wide variety of
applications towards public-key cryptography
algorithms. In essence, a Galois field is an algebraic
structure with established operations for addition,
subtraction, multiplication, and division that satisfy
the requirements for an Abelian group. This means
that operations follow the five axioms of an Abelian
group: closure, associativity, commutativity, having
an identity element and an inverse element. Most
importantly, Galois fields have a finite number of
elements in them (Lidl and Niederreiter, 1997).
The most efficient and secure cryptographic
system in use today is known as elliptic curve
cryptography (ECC) and is based on the concept of
elliptic curves built over Galois fields (Koblitz,
1987). Our research in particular investigates elliptic
curves built over Galois fields of characteristic 3.
This essentially means that the number of elements
in the field is a power of 3, allowing the Galois field
to be notated as GF(3
k
), where k represents the
degree of the field. In Galois fields of characteristic
3, elements of the field are represented as
polynomials modulo a primitive polynomial p(x),
where coefficients are either 0, 1, or 2 (Lidl and
Niederreiter, 1994). A primitive polynomial is an
irreducible polynomial of degree k - 1 that can
generate all elements of the field. After the research
of Galbraith (2001), it is well accepted that
characteristic 3 curves provide more security and
bandwidth efficiency than conventional binary or
prime curves. In addition, they are highly applicable
towards building pairing-based cryptosystems, an
attractive option for identity-based cryptographic
algorithms (Boneh and Franklin, 2001). However,
according to the canonical research of Harrison,
Page and Smart (2002), they are not efficient enough
despite their potential. This is mainly because
characteristic 3 polynomial arithmetic operations
rely on base 3 arithmetic (Figure 1) and are much
slower compared to prime and binary Galois fields,
which utilize the computer’s inherent hardware
arithmetic.
Figure 1: Base 3 Arithmetic.
Elliptic curves are a type of equation of the
form y
2
= x
3
+ ax + b, where a and b represent
integer coefficients. When elliptic curves are built
531
S. Iyengar V..
Efficient Characteristic 3 Galois Field Operations for Elliptic Curve Cryptographic Applications.
DOI: 10.5220/0004528105310536
In Proceedings of the 10th International Conference on Security and Cryptography (SECRYPT-2013), pages 531-536
ISBN: 978-989-8565-73-0
Copyright
c
 2013 SCITEPRESS (Science and Technology Publications, Lda.)

over a Galois field, the points on the curve
themselves form an Abelian group making it
possible for operations to be done on points on the
curve such as addition of two points, where the
result is a third point on the curve, as shown on the
left of Figure 2 (Hankerson et al.). This form of
elliptic curve is known as the Weierstrass equation
and is the most standard form of elliptic curve used
in number theory (Koblitz, 1994). Another form of
elliptic curve that is popular is the Edwards equation
(right side of Figure 2) of the form x
2
+ y
2
= 1 +
dx
2
y
2
, where d represents a coefficient. Our research
works primarily with the Edwards form of elliptic
curves due to the lack of characteristic 3 Edwards
research in the past.
Weierstrasss: y
2
= x
3
+ ax + b Edwards: x
2
+ y
2
= 1 + dx
2
y
2
Figure 2: Geometric Representation of Weierstrass
Addition (“What is Diffie-Hellman”, n.d) and Graphical
Representation of Multiple Edwards Curves (“Edwards
Curve”, n.d).
Given the fact that operations can be performed
on points on an elliptic curve, it is possible to design
cryptographic algorithms based on difficult number-
theoretic problems within this group (Silverman,
2006). For ECC this difficult problem is the Elliptic
Curve Discrete Logarithm Problem (ECDLP), which
states that it is difficult to find a point P and integer
k, given their product Pk. This operation of
multiplying a point by an integer is referred to as
scalar multiplication. Scalar multiplication not only
dominates the execution time of ECC algorithms,
but is also essential to the security of these systems.
1.1 Related Work
The research of Harrison, Page and Smart is
regarded as the canonical paper on software
implementation of characteristic 3 Galois fields for
ECC applications. Their research uses conventional
algorithms for polynomial arithmetic, and then
provides software optimization. Research by Iyengar
has developed efficient scalar multiplication
algorithms. Three of these algorithms are use
extensively in this research: the Binary Double-Add
Algorithm, the Ternary Expansion Algorithm, and
the Balanced Ternary Expansion Algorithm.
1.2 Research Goals
This research has two main goals:
1. To design and implement characteristic 3 Galois
field operations with greater overall efficiency than
conventional state-of-the-art algorithms.
2. To analyze this new method’s applicability to
elliptic curve cryptography.
Overall efficiency is evaluated as a combination
of a comparison of implementation speeds, and
time-space tradeoffs. If a new and more efficient
method for characteristic 3 Galois field operations
can be developed, it would be a major advancement
for elliptic curve cryptography and Internet security
in general.
2 CONVENTIONAL
ALGORITHMS
Algorithms 1 – 6 are the characteristic 3 Galois field
algorithms as presented in the research of Harrison,
Page and Smart, 2002. They are widely considered
the most efficient characteristic 3 algorithms in
literature.
Algorithm 1: Characteristic 3 Polynomial
Addition/Subtraction
INPUT: Polynomials f(x) = [a
n
…a
1
, a
0
]
and g(x) = [b
m
…b
1
, b
0
]
OUTPUT: f(x) + g(x)
1. For i from 0 to n if n > m,
from 0 to m if m > n
a. P
i
= (a
i
+/− b
i
) % 3
2. Return P(x)
Algorithm 3: Conventional Characteristic 3
Polynomial Multiplication
INPUT: Polynomials f(x) = [a
n
…a
1
, a
0
]
and g(x) = [b
m
…b
1
, b
0
]
OUTPUT: f(x) *g(x)
1. For i from 0 to n
a. For j from 0 to m
i. P
i+j
= (a
i
* b
j
) % 3
2. Return P(x)
Algorithm 4: Conventional Characteristic 3
Polynomial Cubing
INPUT: Polynomial f(x) = [a
n
…a
1
, a
0
]
OUTPUT: f(x) ^ 3
1. For i from 0 to n
a. P
i * 3
= (a
i
* 3) % 3
SECRYPT2013-InternationalConferenceonSecurityandCryptography
532

Conventional characteristic 3 polynomial cubing
takes the degrees of all terms of f(x), and multiplies
them by 3. The resulting polynomial is then reduced
modulo the primitive polynomial of the system.
Algorithm 5: Conventional Characteristic 3
Polynomial Division
INPUT: Polynomials f(x) = [a
n
…a
1
, a
0
]
and g(x) = [b
m
…b
1
, b
0
]
OUTPUT: f(x) / g(x)
1. h(x) = Extended Euclidean
Algorithm Inverse of g(x)
2. Return h(x) * f(x)
Conventional characteristic 3 polynomial division is
a complex operation requiring multiple steps.
Firstly, the inverse of the divisor is taken using
Algorithm 6. This is then multiplied by the dividend
using Algorithm 3.
Algorithm 6: Extended Euclidean Algorithm
INPUT: Polynomial f(x) = [a
n
…a
1
, a
0
],
Primitive Polynomial p(x)
OUTPUT: f
-1
(x)
1. remainder[1] = p(x);
remainder[2] = f(x)
2. inverse[1] = 0; inverse[2] = 1
3. i = 2
4. while remainder[i] > 2
a. i = i + 1
b. remainder[i] = remainder[i-2]
mod remainder[i-1]
c. quotient[i] = remainder[i-2] /
remainder[i-1]
d. If(inverse[i] == 2) inverse[i]
= 2(-quotient[i] *
inverse[i-1] + inverse[i-2])
e. Else (inverse[i] = -
quotient[i] * inverse[i-1] +
inverse[i-2])
f. Return inverse[i]
3 KEY RESEARCH CONCEPTS
The key idea of this research was to map the
polynomials to a simpler representation more
conducive to efficient arithmetic. The algorithms
designed were inspired by the concept of Zech’s
logarithms presented in the work of Lidl and
Neiderreiter, 1997. The algorithms designed include
the following: logarithm table generation,
polynomial multiplication, polynomial division, and
polynomial cubing.
3.1 Our Novel Contributions
This research designed and developed a new and
highly efficient way of doing characteristic 3 Galois
field operations using a logarithm-table approach.
Furthermore, this research explored and analyzed
Edwards curves over characteristic 3 fields. Finally,
scalar multiplication was implemented using binary,
ternary, and balanced-ternary algorithms.
Algorithm 7: Logarithm Table Generation
INPUT: Primitive Polynomial P(x)
OUTPUT: Mapped table of field elements
and logarithms
1. LogTable[0] = x
2. For i from 1 to field size do
a. LogTable[i] =
LogTable[i-1] * x
b. if degree of LogTable[i]=
degree of P(x) do
LogTable[i] modulo P(x)or
substitution reduction
3. Return LogTable
The logarithm table generation algorithm aims to
create a table of field element logarithms, mapped
from a power representation. This is done by
repeatedly multiplying successive terms in the table
by the value x, and then reducing these values
modulo the primitive polynomial of the system. This
algorithm also utilizes the concept of substitution
reduction to simplify polynomial modular reduction.
Substitution reduction basically substitutes, during
the computation phase, an identity previously
computed in the table, in order to simplify modular
reduction. To better illustrate this concept, we have
created a small example of logarithm table
generation as shown in Figure 3.
Figure 3: Example of Logarithm Table
Generation and Use
The following example shows the creation of a log
table for the Galois Field 3
3
over the primitive
polynomial P(x) = x
2
+ 2x + 2
Power
Rep
Galois Field
Rep
Operation Done
1 1
x x 1  x
x
2
x + 1 x
2
mod x
2
+ 2x + 2
x
3
2x + 1 x
2
+ x = 2x + 1
x
4
2 2x
2
+ x = 2
x
5
2x 2  x
x
6
2x + 2 2x
2
= 2x + 2
x
7
x + 2 2x
2
+ 2x = x + 2
x
8
1 x
2
+ 2x = 1
EfficientCharacteristic3GaloisFieldOperationsforEllipticCurveCryptographicApplications
533

This example computes the table in 8 multiplications
by x, and just 1 modular reduction using repeated
substitution with the identity x
2
= x + 1.
Once created, the logarithm table can then be
used to perform the following operations very
efficiently:
Polynomial multiplication and modular
reduction: Addition of power representation
exponents – EX: (x + 1)  (2x + 1) = x
2
 x
3
= x
5
=
2x
Polynomial division and modular reduction:
Subtraction of power representation exponents –
EX: (2x + 2) / 2 = x
6
/ x
4
= x
2
= x + 1
Polynomial exponentiation and modular
reduction: Multiplication of power representation
exponent by the desired exponent – EX: (2x + 1)
2
=
(x
3
)
2
= x
3

2
= x
6
= 2x + 2
3.2 Implementation
The main instrument used in this research was a
Windows 7 computer with a 2.10 GHz Intel Core i3
processor installed with a Microsoft Visual Studio
compiler. The main program was written in C++. An
open source implementation for a Galois Field of
characteristic 2 (Partow, 2006) was used as the
starting point for the programming part of the
research. The algorithms for the Galois Field of
characteristic 3 were designed independently and
then implemented into the program for testing.
Primitive polynomials were generated for each
Galois field size using the open source software
Primpoly (O’Connor, 2013).
4 RESULTS AND DISCUSSION
4.1 Galois Field Operations
The first goal of this research was to design and
implement characteristic 3 Galois field operations
more efficient than conventional algorithms. These
algorithms were tested by performing operations on
a wide range of values within Galois fields of six
different sizes: 3
5
, 3
7
, 3
9
, 3
11
, 3
13
, 3
15.
These
operations were measured in terms of processor
cycle counts, and finally averaged out as an
indication of the algorithms’ overall efficiencies.
Table 1 compares the average speed of these
operations using both the logarithm table method
designed in this research and the conventional
methods.
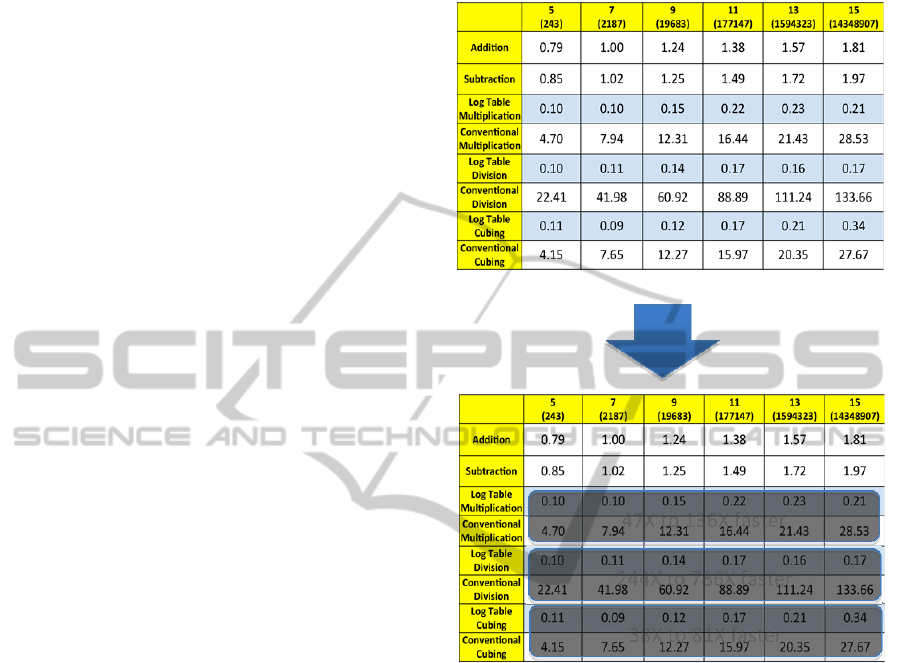
Table 1: Comparison of Performance of Galois Field
Operations (Processor Clock Cycles).
Degree of Galois Field
As shown in Table 1, the logarithm table
methods of doing basic characteristic 3 Galois field
operations were orders of magnitude faster than their
conventional counterparts. To conclude, research
goal 1 was met.
4.2 Elliptic Curve Analysis
Research goal 2 was to evaluate the applicability of
the logarithm table method towards elliptic curve
cryptography. The underlying Galois Field was thus
implemented, tested, and verified over Edwards
elliptic curves. This basically involved timing scalar
multiplication operations using the Binary Double-
Add, the Ternary Expansion, and the Balanced
Ternary Expansion algorithms for Edwards curves
using six different Galois field sizes: 3
5
, 3
7
, 3
9
, 3
11
,
3
13
, 3
15
. This procedure was first done using the
conventional polynomial arithmetic operations.
47Xto136Xfaster
38Xto81Xfaster
244Xto786Xfaster
SECRYPT2013-InternationalConferenceonSecurityandCryptography
534

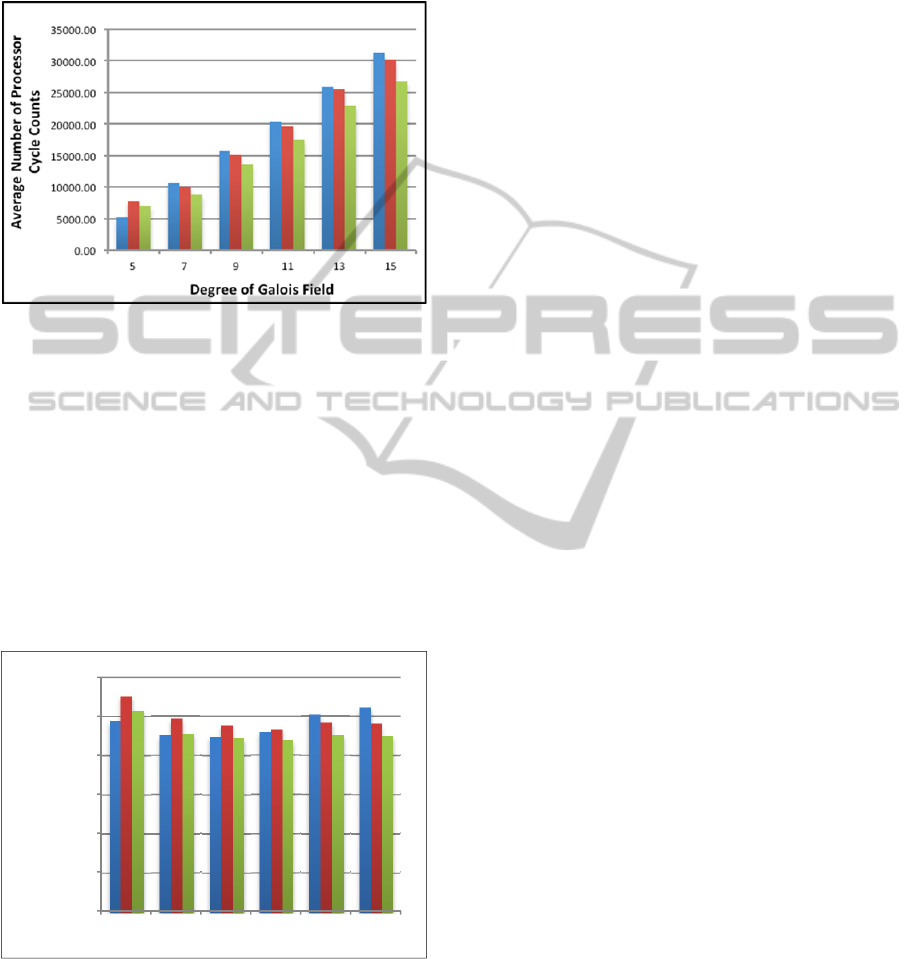
Figure 4: Elliptic Curve Scalar Multiplication -
Conventional Polynomial.
Figure 4 shows the average performance of
scalar multiplication algorithms over 6 Galois field
sizes using the conventional characteristic 3
arithmetic algorithms. The Balanced Ternary
Expansion algorithm is the most efficient for all
Galois field sizes except 3
5
. Furthermore, as the size
of the underlying Galois field increases, the
efficiency decreases in a linear manner.
This same scalar multiplication testing procedure
was applied with the logarithm table method for
polynomial arithmetic.
Figure 5: Elliptic Curve Scalar Multiplication – Logarithm
Table.
Figure 5 shows the average time for scalar
multiplication operations over the 6 different Galois
fields with the 3 different scalar multiplication
algorithms using logarithm table polynomial
operations. It is clear that the Balanced-Ternary
algorithm is generally the fastest, and as the size of
the field increases, the speed of all algorithms
remains constant. Most importantly, these operations
are significantly faster in comparison to their
conventional counterparts shown in Figure 4.
Specifically, the logarithm table method for scalar
multiplication ranges from ~5X faster for a field of
degree 5, to ~30X faster for a field of degree 15.
4.3 Next Steps
A very attractive option for future research is
developing a hybrid method that utilizes both
logarithm table and conventional arithmetic,
reducing the cost upfront and the storage needed,
while also taking advantage of the speed provided
by logarithm table-based arithmetic. This could be
done by using a logarithm table method for a small
subfield, and then extending this field to a larger
power. Also, next steps include testing larger
numbers such as NIST (National Institute for
Standards in Technology) size elliptic curves in
order to evaluate the scalability of these algorithms.
5 CONCLUSIONS
In this paper, we present a novel and efficient
method for characteristic 3 Galois field operations
and analyze this method’s distinctive applications to
elliptic curve cryptography. We thus meet both
research goals. The findings of this research have a
wide significance towards the findings of other
researchers such as Harrison et al. and those at NIST
who have disregarded characteristic 3 Galois fields
for elliptic curve cryptographic applications. This
research shows that in fact characteristic 3 can be a
feasible option for some ECC applications.
ACKNOWLEDGEMENTS
My teacher and sponsor Peter Langley for all his
help and encouragement. My mentor Dr. Neal
Koblitz, Professor of Mathematics at the University
of Washington for his guidance and continuous
support. Dr. Jiangtao Li of Intel Corporation for
reviewing my research paper and providing useful
feedback.
0,00
200,00
400,00
600,00
800,00
1000,00
1200,00
5 7 9 11 13 15
AverageNumberofProcessor
CycleCounts
DegreeofGaloisField
Legen
d
for Figures 4 and 5
 Binary Double-Add
 Ternary Expansion
 Balanced Ternary Expansion
EfficientCharacteristic3GaloisFieldOperationsforEllipticCurveCryptographicApplications
535

REFERENCES
Ahmadi, O., Hankerson, D., & Menezes, A. (2007).
Software implementation of arithmetic in. Arithmetic
of Finite Fields, 85-102.
Barreto, P., Kim, H., Lynn, B., & Scott, M. (2002).
Efficient algorithms for pairing-based cryptosystems.
Advances in Cryptology—CRYPTO 2002, 354-369.
Bernstein, D., & Lange, T. (2007). Faster addition and
doubling on elliptic curves. Advances in Cryptology,
13, 29-50. Retrieved from http://cr.yp.to/newelliptic/ -
20070906.pdf
Blake, I., Seroussi, G., & Smart, N. (1999). Elliptic curves
in cryptography. (1st ed.). London: Cambridge
University Press.
Boneh, D., & Franklin, M. (2001). Identity-based
encryption from the Weil pairing. In Advances in
Cryptology—CRYPTO 2001 (pp. 213-229). Springer
Berlin/Heidelberg.
Das, A., & Madhavan, C. E. V. (2009). Public-key
cryptography: theory and practice. (1st ed.). New
Delhi: Dorling Kindersley.
Galbraith, S. (2001). Supersingular curves in
cryptography. Advances in Cryptology—ASIACRYPT
2001, 495-513.
Hankerson, D., Menezes, A., & Vanstone, S. (2004).
Guide to elliptic curve cryptography. (1st ed.).
Springer.
Harrison, K., Page, D., & Smart, N. P. (2002). Software
implementation of finite fields of characteristic three,
for use in pairing-based cryptosystems.LMS
Journal of Computation and Mathematics, 5(1),
181-193.
Iyengar, V. S. (2012). Novel elliptic curve scalar
multiplication algorithms for faster and safer public-
key cryptosystems. International Journal on
Cryptography and Information Security, 2(3), 57-66.
doi: 10.5121/ijcis.2012.2305
Koblitz, N. (1994). A course in number theory and
cryptography. (2 ed.). New York, NY: Springer
Koblitz, N. (1987). Elliptic curve
cryptosystems. Mathematics of Computation, 48(177).
203–209. Retrieved from http://www.ams.org/
journals/mcom/1987-48-177/S0025-5718-1987-
0866109-5/S0025-5718-1987-0866109-5.pdf
Lawson, N. (2009). Side-channel attacks. IEEE, 7(6), 65-
68. Retrieved from http://rootlabs.com/articles/
IEEE_SideChannelAttacks.pdf
Lidl, R. and Niederreiter, H. Introduction to Finite Fields
and Their Applications, rev. ed. Cambridge, England:
Cambridge University Press, 1994.
Lidl, R. and Niederreiter, H. (Eds.). Finite Fields, 2nd ed.
Cambridge, England: Cambridge University Press,
1997.
O’Connor, S.E. (2013) Primpoly (Version 11.0)
[Computer Software] Available from: http://www.
seanerikoconnor.freeservers.com/Mathematics/Abstrac
tAlgebra/PrimitivePolynomials/overview.html
Partow, A. (2006) Galois Field Arithmetic Library
(Version 5.0) [Computer Software] Available
from:
http://www.partow.net/projects/galois/#GFALLice nse
Silverman, J. H. (2006). A friendly introduction to number
theory.
(3rd ed., Vol. 3). Pearson Prentice Hall.
What is diffie-hellman (n.d.). RSA Labs: PKCS, 7,
Retrieved from http://www.rsa.com/rsalabs/
node.asp?id=2248
(2012). Edwards Curve. Wikipedia, the free encyclopedia,
Retrieved from http://en.wikipedia.org/wiki/
File:Edward-curves.svg
SECRYPT2013-InternationalConferenceonSecurityandCryptography
536