A Metamodel-driven Architecture for Generating, Populating
and Manipulating “Possible Worlds” to Answer Questions
Imre Kilián
1
and Gábor Alberti
2
1
Department of Informatics, University of Pécs, H-7624 Pécs, Ifjúság útja 6, Hungary
2
Department of General Linguistics, University of Pécs, H-7624 Pécs, Ifjúság útja 6, Hungary
Keywords: Representational Dynamic Discourse Semantics, Information State, Modal Logic.
Abstract: The architecture we are developing can serve many ends: it can be used, for instance, as an intelligent
personal diary for private purposes, or even as a dynamic “epistemic” protocol for legal cases or criminal
investigations. Two of its special features make our architecture capable of performing these tasks. One of
them is a DRT-based (Kamp et al., 2011) formal cognitive theory called eALIS (Alberti, 2009; Alberti
and Kleiber, 2012; Alberti and Károly, 2012), which is responsible for the particular structure of our
databases; the other one is a Prolog-based logical framework, which is responsible for populating the
database and for logically “closing” its appropriate substructures. The major contribution of eALIS to this
project is a traditional relational model (w
0
) of the relevant segment of the external world coupled up with
an unlimited set (W={w
1
,w
2
,…}) of “wordlets”, each of which is an appropriately modified and highly
partial copy of w
0
, capable of registering the beliefs, desires and intentions of a group of people, as concerns
the facts of w
0
at selected points of time (T), as well as one another’s beliefs and other wordlets of WT.
The Prolog inference system operates on a partially ordered structure with which we furnish WT, in order
to answer users’ yes/no questions and to provide entities of wordlets as answers to wh-questions
1 THE ARCHITECTURE
OF THE SYSTEM
The architecture shown in Figure 1 is shared by
several eALIS-based projects. What this particular
project focuses on is the generation of a partially
ordered tree of worldlets with w
0
, “the external-
world model”, at its roots; the population of these
wordlets with entities, relations/predicates; and,
finally, the appropriately localized manipulation of
these entities by Prolog inference steps. One of our
other projects is responsible for the continuous
extension of the linguistic fragments that users’
input questions are to be based upon.
2 GENERATING WORLD(LET)S
As shown in Figure 1, the World-Model Generator is
clearly distinguished from the Module of World-
Model Population.
Why? The answer lies with our approach in
which the former module is practically an interface
Figure 1: System Architecture.
which enables the user to define either a new
worldlet, or a new predicate, or a new entity, or to
create an intersection of the world at a given point of
time. It is the programmers’ task to write a program
so that the user’s each and every request is followed
by a query concerning the provision of data that
should satisfy the request. The only task of the user
World Model
Generator
Linguistic
Generator
World-
Model
Population
Truth-model Interpretation
+ Dynamic Interpretation
Lexicon
Population
+
Logical
Operations
+
Cultural/
Encycl.
Knowledge
74
Kilián I. and Alberti G..
A Metamodel-driven Architecture for Generating, Populating and Manipulating “Possible Worlds” to Answer Questions.
DOI: 10.5220/0004596000740078
In Proceedings of the 8th International Joint Conference on Software Technologies (ICSOFT-EA-2013), pages 74-78
ISBN: 978-989-8565-68-6
Copyright
c
2013 SCITEPRESS (Science and Technology Publications, Lda.)

is to provide the required data; this procedure is, in
fact, the actual population of the world model. The
person responsible for the Module of World-Model
Population, thus, is the writer of the diary or the
legal expert himself (cf. Abstract). He/she is the one
who can and should describe the part of the external
world relevant to him/her (e.g. as in a complex legal
case), as well as all the beliefs, desires and intentions
that he/she attributes to the agents who he/she
qualifies as relevant participants/observers in the
given case.
In what follows, we shall overview the procedure
of the query from the user’s perspective.
3 POPULATING THE WORLD
MODEL
Due to the reciprocal and lifelong character of our
discourse-semantic background (Reciprocal And
Lifelong Interpretation System → hence, eALIS),
what we use as a world model is not only a
representation of (a part of) “the world outside” but
also a representation of people’s temporary
information states—since human beings together
with their minds’ content form part of the world.
Practically, the relational model of the relevant
external situation multiplies in an arbitrarily
proliferating manner of “mutation”. A person’s
desire, for instance, can be represented by providing
some of the external relations/facts (1a), typically
with opposite polarity values (1b). A complex belief
can also be construed as a mutation of external facts
in respect of polarity (1c):
(1) a. 1. Mary is gorgeous. (+: This is true.)
2. Mary loves Peter. (+: This is true.)
3. Mary loves John. (–: This is false.)
b. 1. Mary is gorgeous. (+: This coincides with
John’s desire.)
2. Mary loves Peter. (–: This does not belong
to John’s desires.)
3. Mary loves John. (+: This is John’s
desire.)
c. 1. Mary is gorgeous. (+: This is John’s
opinion.)
2. Mary loves Peter. (+: John knows that this
true.)
3. Mary loves John. (+: John believes that
this is true.)
We multiply worlds, but the external-world model is
retained as a standard simple information structure,
in which “[Axiom 10] No argument is an infon,
relation or role”, to avoid the theoretical
complications discussed in (Seligman and Moss,
1997) (NB. Axiom 10 is violated in the highly
partial constructions we call wordlets). (2a) below
shows an infon i which belongs to w
0
at moment t
and expresses the piece of information that defines if
entities u
1
, u
2
, ..., u
k
stand in a k-ary relation p.
(2) a. p(w0, t, +, i, u1, u2, ..., uk)
b. p(w, t, +, e, r1, r2, ..., rk)
c. lambda(w', w", ...)
d. +/–//0/0
e. DES,r
John
,t,–^BEL,r
John
,t,0
f. alpha(u, r, ...), and alpha(r', r", ...)
In (2a), ʻ+ʼ can be replaced with ʻ–ʼ or ʻʼ. These
polarity values mean, respectively, that the entities
in question stand in a given relation (e.g. the pair of
Peter and Mary, at moment t, belong to a set of pairs
of people which consists of pairs where the first
element loves the second one, at t; i.e., “Peter loves
Mary”) / are outside of the given relation (“Peter
does not love Mary at the given moment”) / do not
belong to the domain of the given relation (it does
not make any sense to register e.g. “the table loves
Mary” in the model of the external world).
Thus, the external world at moment t can be
described by means of Prolog-facts, similarly to (1a).
In the case of each k-ary relation p, the Cartesian
product U
k
is partitioned into three subsets in the way
described above (+/–/), where U is the set of
external entities, fixed once and for all (NB. If a
person is associated with a predicate at moment t
when he/she does not exist, i.e. before his/her birth
or after his/her death, the polarity value ʻʼ
(“meaningless”) is to be applied).
The formula in (2b) above is a “true copy” of the
formula in (2a) in an arbitrary worldlet w. The u
i
external entities have been replaced with r
i
internal
entities, and w has been substituted for w
0
.
Furthermore, infon i is replaced with an eventuality e.
Instead of a “true copy”, mutated copies can also be
produced by choosing a polarity value (out of the set
shown in (2d) above) which differs from the polarity
value in the Prolog-fact serving as the source of copy.
Here the ʻ+ʼ should be replaced with a ʻ–ʼ, for
example; which would mean that a positive fact is
believed or desired to be negative in a worldlet of
belief/desire. If a ʻ0ʼ appears in the place of a ʻ+ʼ in
the source, then the positive source fact is not known
or not desired in the target worldlet of belief/desire.
(2c) shows the scheme of the Prolog-fact
providing the relation between a worldlet (of
someone’s belief/desire/intention) and the external-
world model, or between two worldlets. The series
of points in (2c) shows the place in the formula
where the position of w" is to be given relative to
AMetamodel-drivenArchitectureforGenerating,PopulatingandManipulating"PossibleWorlds"toAnswerQuestions
75

that of w' in the “tree of worldlets” mentioned above.
In the theory of eALIS (Alberti, 2009; Alberti and
Kleiber, 2012; Alberti and Károly, 2012), this piece of
information is called a lambda-label. If w', for
instance, is the worldlet of Peter’s belief, then w" is
defined as the worldlet consisting of the situations
that, in Peter’s opinion, John does not long for, if the
lambda-label is DES,r
John
,t,–. (2e) illustrates the
application of the special polarity value marked by a
crossed-out zero: if eventuality (1b.3) is associated
with the polarity-segment label mentioned in (2e), this
means that John wants to know if Mary loves him or
not. The decisive part of the calculus of ʻ0ʼ is that this
desire is satisfied by receiving either a positive or a
negative answer.
Anchoring relations between entities of w' and
entities of w" must also be given (2f).
The copying and mutating of infons of the
external-world model in internal worldlets does not
belong to the task of the programmer. The polarity
values are permitted to stand in an arbitrary relation,
depending on the legal or private case that the user of
our system intends to model. What the software
evaluates via its Module of Truth-Conditional
Interpretation (see Figure 1 above), is practically the
system of polarity values that belongs to the same
relation/predicate. As some values pertain to beliefs,
desires and intentions at different moments, their
comparison enables us to define “numerically” such
pragmatic things as lie, bluff or convincing. Due to
Prolog, an existential piece of information (say,
“Mary loves someone”) can also be evaluated so that,
in addition to a yes/no answer, we can also receive the
entities satisfying the existential statement.
4 LOGICAL FRAMEWORK
Choosing Prolog as a programming language also
means choosing logics as a modelling tool, and
generally choosing logic programming as an
implementation paradigm. For modelling the multi-
agent world along with its belief-desire-intention
(BDI) mental relationship, eALIS uses an
epistemic/temporal multimodal logic framework and
an appropriate logic language (eALIS Modal
Language/eALM).
Beyond the logic framework and the language,
the target model and/or the runtime-environment
must also be defined. Owing to Prolog, the closer the
target model to pure first-order logic, the more
efficient the inference. We simply intend to use
Prolog, whenever possible, as a theorem-proving
engine based on linear input resolution. If this
strategy is not satisfactory, the necessary
enhancements have to be made.
Questions are basically answered by the
theorem-prover. Theorem proving, however, is not
complete: it follows human interpreters’ capabilities.
Instead of less efficient mathematical proofs for each
provable theorem, we aim to use a mixed-strategy
theorem-prover which combines the results of
theme-dependent but quick solvers (Kilián, 2007).
On the level of Prolog implementation we define a
controlling meta-language which enables the system
to control the different external solvers that may be
plugged-in.
In order to map modal-logic statements to first-
order logic, we apply a slightly improved version of
Ohlbach’s mapping rules (Ohlbach, 1988).
According to this, each literal statement is extended
with two new logical parameters. One describes the
epistemic modal context of the statement
(practically, it denotes the “wordlet” where the
literal statement is valid). The second extra
parameter describes the temporal context (and/or the
actual time). This representation enables the easy
mapping of modal logic axioms.
Some of the modal axioms are stored in an
explicite form: compiled into the knowledge base.
This means that, for each piece of knowledge, new
rules are to be added which perform the possible
inferential steps. Although this allows for the
immediate utilisation of the Prolog engine, at the
same time it multiplies storage demand. Therefore
we only follow this approach with the most
frequently used axioms (e.g. inheritance). The rarely
used axioms are interpreted by a meta-interpreter,
rather than compiled.
Being an interpretation framework for natural
languages, eALIS uses multi-valued logics (True,
False, Not provable, Meaningless, etc.). This also
correlates with the Open World and Closed World
Assumptions: wherever Closed World cannot be
applied, a „Not provable” result must be returned.
Whenever the usage constraints of certain predicates
are violated, the inference engine should generate
„Meaningless” value. In the future, the logical
framework may need to be extended even to a fuzzy
model.
5 METAMODEL
We use the word ’meta-’ in reference to the
description of a target structure. In object-oriented
technology, the mass of data that a software
ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies
76

manipulates is described by a model – the data are
instances of the model. For common software
products, the model is fixed, and a common
programming language implements it. In certain
cases, however, the model can develop over time
and we must also regard this as part of the data of
the software. The model for such a software cannot
be fixed: the metamodel, that is the model of the
model is fixed and programmed.
The application data for eALIS are individual
entities, their actual relationships and the inference
rules governing them. The layer over them is the
model layer that contains the description of
predicates, classes, properties etc. of the individual
layer. These together form the knowledge-base of
the software.
For the seamless handling of these two layers,
the structure of the model-layer must also be
described. This is called the metamodel describing
what the model looks like.
Moreover, we can suppose that even the
metamodel cannot be fixed as it is continuously
corrected in the course of software development.
Therefore, we must also define the model of the
metamodel (the meta-metamodel), which can be
finally hard-coded (Kilián, 2008).
The four-layer structure described above has
been introduced by OMG for object-oriented
software (OMG, 1997).
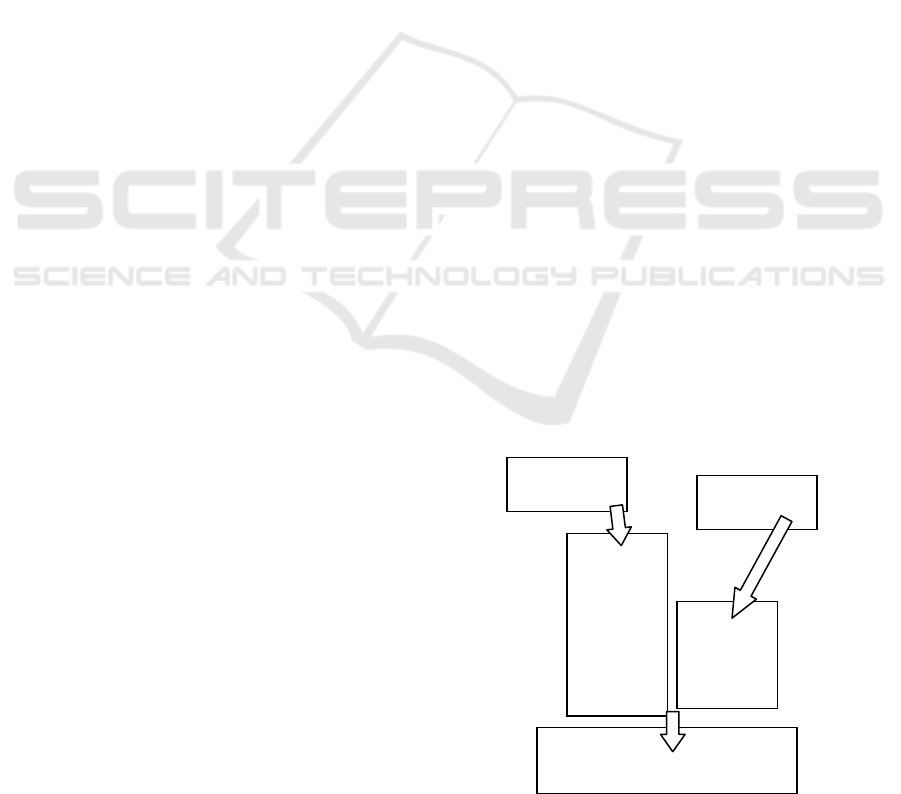
Figure 2: Four level metamodel structure.
The most important relation between the application
data is the wordlet structure. The superindividual
layer of this describes those groupings and usage-
environments that collect the common knowledge of
several individual actors.
The individual layer of the wordlet structure
mostly contains individuals who interpret texts, but
we also map other text-interpreting contexts here,
e.g., literary works or legal cases.
The supraindividual layer of wordlets has a
forest topology the roots of which are the individuals
themselves. A wordlet from this layer always has
reference to its ancestor, thus they are not to be
defined explicitly.
6 EXPORT/IMPORT
AND INFERENCE
In research there have been a number of ontologies
designed over the past decade. There are so called
‘upper-level ontologies’ which contain the most
general and abstract concepts of our knowledge, but
there are also specialized ‘domain ontologies’ for
narrow special fields. It would be a serious mistake
to not utilize the ontologies developed so far. The
system must be equipped with a plug-in-like
extendable import/export interface. The first such
plug-in loads the OWL ontologies of the Semantic
Web initiative.
Another export/import requirement is to store
instance-information in a relational database, and to
load them in a lazy way, only when it is necessary.
The most straightforward solution maps a class to a
relational table, and an instance to a line in a table.
Since the indexing mechanism is only efficient for
more than thousands of data, for classes with less
instances of data, a simple Prolog textual export can
be much more efficient.
The elements of the knowledge-base that were
compiled directly can also be invoked directly, by
Prolog. For the overall architecture, a plug-in-
interface is proposed which enables the system to
invoke externally connectable inference engines.
One such possibility is to use Contralog (Kilián,
2011) which builds a forward chaining inference
engine upon Prolog. As another possibility, meta-
interpreters can easily be designed in Prolog. For
certain decidable subsets of mathematical logics,
however (e.g. for description logics, DL), there are
free inference engines available which can be
downloaded or invoked as a Web application.
7 CURRENT STATUS
AND FUTURE WORK
The integration of OWL ontologies, their modal
extension and model-driven integration have been
successfully completed, and the system is under
extensive testing. The integration of the Contralog
forward-chaining framework is also successful.
Based on our experience, we have redesigned the
system to meet the requirements of metamodell-
driven architecture, and to implement the plug-in
Entities/relationships
Predicate definitions
Metamodel
(description of the
model
)
Meta-metamodel
AMetamodel-drivenArchitectureforGenerating,PopulatingandManipulating"PossibleWorlds"toAnswerQuestions
77

interface for import-export operations and for
external inference engines. This phase is still under
development. The completion of this step can open
new ways to extensive language-technological
experiments. As soon as the engine is coherent, we
are planning to extend it by a Java GUI.
ACKNOWLEDGEMENTS
We are grateful to a Hungarian national fund for
their contribution to our costs at ICSOFT 2013
(Reykjavík): SROP-4.2.1.B-10/2/KONV/2010/
KONV-2010-0002 (Developing Competitiveness of
Universities in the Southern Transdanubian Region).
Writing this paper is due to another project: SROP-
4.2.2.C-11/1/KONV-2012-0005 (Well-Being in the
Information Society).
We also express our thanks to our colleagues:
Márton Károly and Judit Kleiber for their
contribution.
REFERENCES
Alberti, G.: eALIS: An Interpretation System which is
Reciprocal and Lifelong. Workshop ‘Focus on
Discourse and Context-Dependence’ (16.09.2009,
13.30-14.30 UvA, Amsterdam Center for Language
and Comm.); http://lingua.btk.pte.hu/realispapers
(2009)
Alberti, G., J. Kleiber Where are Possible Worlds?
(Arguments for eALIS). Acta Linguistica Hungarica
59 (1-2) (ed. Katalin É. Kiss). 3–26. (2012)
Alberti, G., M. Károly: Multiple Level of Referents in
Information State. A. Gelbukh (ed.): Computational
Linguistics and Intelligent Text Processing,
CICLing2012, New Delhi, India. LNCS7181. Springer
Verlag, Berlin, Heidelberg, pp. 34–362 (2012)
Kamp, H., van Genabith, J., Reyle, U.: Discourse
Representation Theory. In Handbook of Philosophical
Logic, vol. 15, pp. 125–394. Springer-Verlag, Berlin
(2011)
Kilián, I.: Modellvezérelt szoftverek készítése I-II (in
English: Creating Model-driven Software) Alkalmazott
Matematikai Lapok MTA, Budapest 2008.
Kilián, I.: Contralog: egy előre haladó Prolog motor és
alkalmazása eALIS nyelvi elemzésre (in English:
Contralog: a Forward-Chaining Prolog Engine and its
Application for eALIS Lingual Parsing) Erdélyi
Magyar Műszaki Tudományos Társaság, SzámOkt
2011. konferencia kiadványa, Kolozsvár, 2011, pp.
199-205.
Kilián, I.: Mixed strategy reasoning. An approach for
resolution based verification of OCL constraints in
UML models, Pollack Periodica, Vol. 2 Supplement,
Akadémiai Kiadó, Budapest 2007.
OMG Joint Revised Submission: Meta Object Facility
(MOF) Specification OMG Document 1997.
Seligman, J., Moss, L. S.: Situation Theory. In van
Benthem, J., and ter Meulen, A. eds.: Handbook of
Logic and Language. Elsevier, Amsterdam, MIT
Press, Cambridge, Mass, pp. 239–309 (1997)
ICSOFT2013-8thInternationalJointConferenceonSoftwareTechnologies
78
