Sampling-based Multi-robot Motion Planning

Zhi Yan, Nicolas Jouandeau and Arab Ali Cherif

Advanced Computing Laboratory of Saint-Denis (LIASD)

Paris 8 University, 93526 Saint-Denis, France

Keywords:

Multi-robot systems, Coordination, Motion planning, Sampling-based method.

Abstract:

This paper describes a sampling-based approach to multi-robot motion planning. The proposed approach

is centralized, which aims to reduce interference between mobile robots such as collision, congestion and

deadlock, by increasing the number of waypoints. The implementation based on occupancy grid map is

decomposed into three steps: the ﬁrst step is to identify primary waypoints by using the Voronoi diagram, the

second step is to generate additional waypoints by sampling the Voronoi diagram, and the last step is to assign

the waypoints to robots by using the Hungarian method. The approach has been implemented and tested in

simulation and the experimental results show a good system performance for multi-robot motion planning.

1 INTRODUCTION

In robotics, the motion planning problem is to pro-

duce a continuous motion from one conﬁguration to

another in conﬁguration space, while avoiding colli-

sion with obstacles. The motion is represented as a

path in conﬁguration space. Motion planning is em-

inently necessary for mobile robot since, by deﬁni-

tion, a robot accomplishes tasks by moving in the

real world (Latombe, 1991). Environments for au-

tonomous mobile robot are usually represented by an

occupancy grid map. For most of motion planning

algorithms, the robot is reduced to a point in a two-

dimensional plane.

Multi-robot motion planning is one of the most

challenging tasks in multi-robot systems. It should

consider not only the obstacles (whether static or dy-

namic) in the environment, but also the possible in-

terference between robots. When robots in a team

are used to perform independent tasks in a shared

workspace, each one will become a mobile obstacle

for the other. Thus each robot should take into ac-

count the movement of other robots. One well-studied

example is the multi-robot space sharing problem

ager and Nebel, 2001) (Luo et al., 2003) (Marcolino

and Chaimowicz, 2009a) (Marcolino and Chaimow-

icz, 2009b) (Luna and Bekris, 2011).

Multi-robot environment must deﬁnitely be dy-

namic, in which motion planning is inherently difﬁ-

cult. Even for a simple case in two dimensions, the

planning is NP-hard and is not solvable in polyno-

mial time (Guo and Parker, 2002). A very common

problem in the motion planning for a group of mobile

robots is when multiple robots move to the same way-

point, causing collision, congestion and deadlock, and

thus affects system performance. We deﬁne this kind

of dynamic standstill of system caused by waypoint

conﬂict as the multi-robot waiting situation problem.

Because, for better or worse, a robot should wait until

the other pass ﬁrst, or all robots should wait for plan-

ner to replan their local trajectories. Therefore, some

kind of mechanism is needed to coordinate the motion

of robots. In this paper, we present a sampling-based

approach based on centralized decision making mech-

anism to multi-robot motion planning. The basic idea

of the proposed approach is to reduce the problem

of waiting situation between robots by increasing the

number of waypoints. The implementation includes

three critical steps:

• The ﬁrst step is toward identifying primary way-

points on top of an occupancy grid map by using

the Voronoi diagram.

• The second step is generating additional way-

points on top of the Voronoi diagram by using a

sampling-based method.

• The third step is toward assigning the waypoints

to robots by using the Hungarian method.

The remainder of the paper is organized as fol-

lows: Section 2 describes an overview of some related

works; Section 3 describes our sampling-based ap-

proach; Section 4 describes the experimental results

549

Yan Z., Jouandeau N. and Ali Cherif A. (2013).

Sampling-based Multi-robot Motion Planning.

In Proceedings of the 10th International Conference on Informatics in Control, Automation and Robotics, pages 549-554

DOI: 10.5220/0004605005490554

 SciTePress

obtained with our approach; and the paper is con-

cluded in Section 5 at last.

2 RELATED WORK

The major approaches to multi-robot motion planning

are expanded from the results of single-robot system.

(Bennewitz et al., 2001) presented an approach based

on A* path planning algorithm to optimize the priori-

ties for decoupled and prioritized path planning meth-

ods for groups of mobile robots. Their approach is

a randomized method which repeatedly reorders the

robots to ﬁnd a sequence for which a plan can be com-

puted and to minimize the overall path lengths. (Guo

and Parker, 2002) proposed an approach based on D*

path planning algorithm which contain two modules:

path planning and velocity planning. The detailed

process can be described as follows: ﬁrst, each robot

plans its own path independently, then a coordina-

tion diagram is constructed based on collision checks

among all robot paths. One approach named artiﬁcial

potential ﬁeld (APF) is used extensively for multi-

robot formation control which is usually linked with

multi-robot motion planning problem. (Tanner and

Kumar, 2005) presented a strategy which can ensure

almost global asymptotic convergence of the robots

to a particular oriented formation shape, while guar-

anteeing collision avoidance in the process.

The approaches often used for high-dimensional

motion planning problems can also be efﬁciently ap-

plied to deal with low-dimensional problems. There

are two major families of approaches known as cell

decomposition and skeletonization. The cell decom-

position method often applied for multi-robot area

coverage problem. (Hazon et al., 2006) presented

an online robust multi-robot spanning tree coverage

(ORMSTC) algorithm based on an approximate cel-

lular decomposition for covering an unknown envi-

ronment. The algorithm is called online because in

which the robots do not have apriori knowledge of

the work area, and it is robust and complete because

in which as long as a single robot is able to move, the

coverage will be completed. A typical skeletoniza-

tion method is Voronoi diagram which is often ap-

plied to the problem of robotic exploration. (Wurm

et al., 2008) presented a strategy for coordinating a

team of exploring robots by using Voronoi diagram

for the segmentation of the environment map. The

strategy extracts the critical points (Thrun, 1998) as

the exploration targets to assign to robots. An al-

ternative to the Voronoi diagrams is the probabilis-

tic roadmap (PRM) (Kavraki et al., 1996) which is

a sampling-based method. (

Svestka and Overmars,

1995) presented a PRM-based approach for multiple

nonholonomic car-like robots motion planning in the

same static workspace, in which the roadmaps for the

composite robot are derived from roadmaps for the

underlying simple robots, and the latter is computed

by a probabilistic single-robot learning method.

The sampling-based methods are currently con-

sidered state-of-the-art for robot motion planning in

complex environments. Because unlike the incremen-

tal heuristic search (such as A* and D*) and the topo-

logical map (such as Voronoi diagram) methods, their

running time does not grow exponentially with the di-

mension of the conﬁguration space, but also easier

to implement. Yet, the sampling-based methods are

probabilistically complete, and can not determine if

no solution exists.

3 OUR APPROACH

3.1 Voronoi Diagram

The ﬁrst step of our approach is to identify primary

waypoints on top of the occupancy grid map by ap-

plying the Voronoi diagram. The Voronoi diagram is

a very popular graph partitioning method for the prob-

lem of map segmentation (Thrun, 1998) (Zivkovic

et al., 2006) (Wurm et al., 2008). For a given map

m, we deﬁne for each point p in the free space S of

m, a set O

(m) which is made up of closest obstacle

points to p. While the Voronoi diagram can be repre-

sented by a graph G(m) = (V, E), where V is the set

of points in O

(m) that are equidistant to at least two

nearest obstacles, and E is the set of edges connecting

two adjacent points in V of m:

V = p ∈ S|

(m)

≥ 2 (1)

E = (p, q)|p, q ∈ V, p adjacent to q (2)

Figure 1 shows the Voronoi diagrams of two experi-

mental maps.

Then the topological map is built based on the

Voronoi diagram. The grid map is decomposed into

a small set of regions separated by narrow passages.

These narrow passages, which are called critical lines,

are found by analyzing a skeleton of the environment.

The partitioned map is mapped into an isomorphic

graph, where nodes correspond to regions and arcs

connect neighboring regions. This graph is the topo-

logical map (Thrun, 1998).

On the basis of the topological map, a series of

points called critical points is generated, at which the

distance to the nearest obstacle in the map is a lo-

cal minimum. In other words, the critical points are

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

550

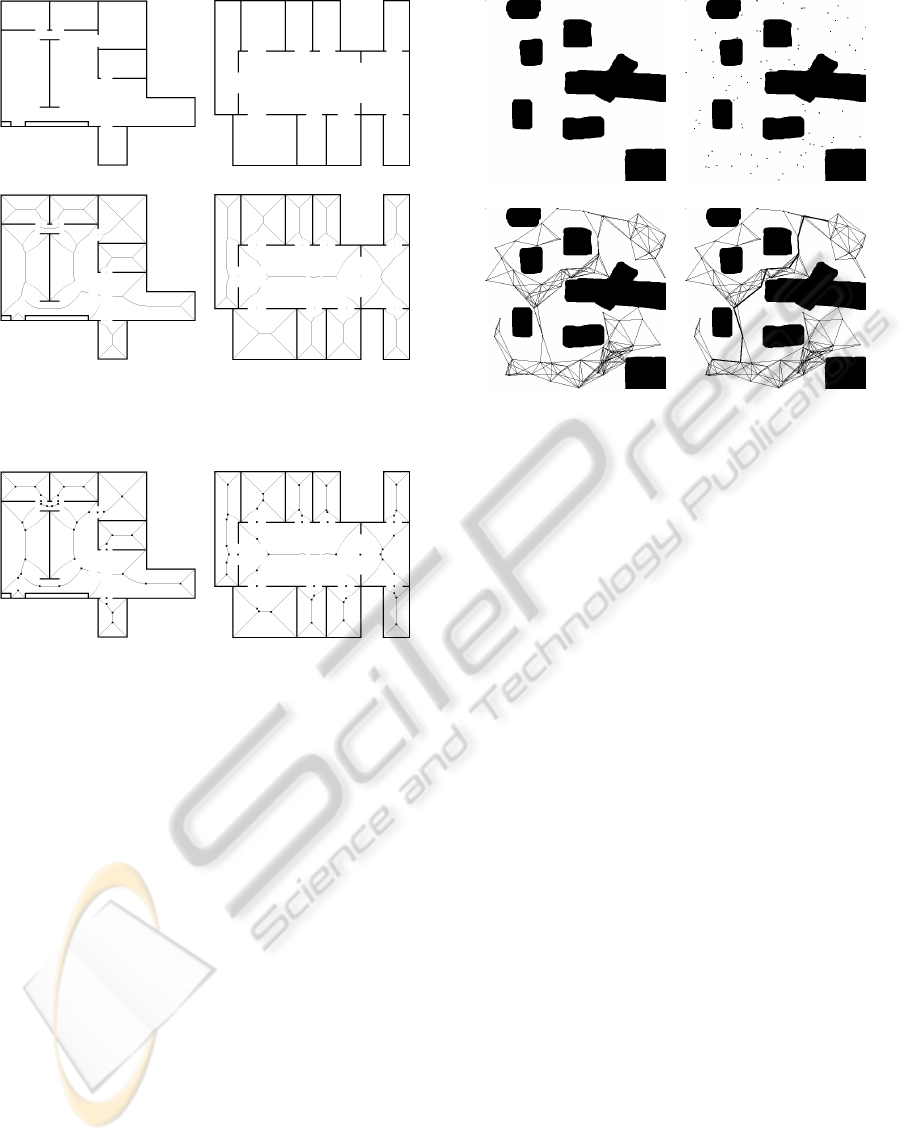
(a) map A (b) map B

Figure 1: Voronoi diagrams of two experimental maps. (a)

and (b) depict the original maps. (c) and (d) depict the gen-

erated Voronoi diagrams.

(a) map A (b) map B

Figure 2: The primary waypoints extracted by using the

Voronoi diagram.

the midpoints of the critical lines. These points are

considered as the primary waypoints for mobile robot

motion planning. Figure 2 illustrates the results of the

ﬁrst step.

3.2 Sampling-based Method

The second step of the approach is to generate addi-

tional waypoints on top of the Voronoi diagram by

applying a PRM-like method. The original PRM is

presented by (Kavraki et al., 1996), of which the ba-

sic algorithmic framework can be summarized as fol-

lows:

• Firstly, randomly sample a sufﬁcient number of

points in the conﬁguration space (denoted by C)

of the robot, keeping any that are not in collision

with obstacles (denoted by C

obs

). This creates a

point set in the the free conﬁguration space (de-

noted by C

f ree

• Secondly, using a local planner (such as straight

line planner), attempt to connect pairs of sam-

(a) (b)

Figure 3: Generation of the probabilistic roadmap. (a)

shows a conﬁguration space in which we will build a proba-

bilistic roadmap. (b) shows the random points generated in

f ree

. (c) shows the roadmap constructed by connecting the

samples relatively close using the straight line planner. (d)

shows a path found by querying the constructed roadmap

using the A* algorithm.

ples that are relatively close to each other by thor-

oughly sampling and collision checking conﬁgu-

rations between them. This creates a graph data

structure called a roadmap.

• Finally, to query the roadmap, ﬁrst attempt to con-

nect the start and goal conﬁgurations to the exist-

ing graph. If that is successful, search the graph

for a path from start to goal using any standard

graph search method (such as A* algorithm).

Like most of motion planning algorithms, the

PRM-like method often computes a collision free

roadmap in a conﬁguration space where the object is

reduced to a point. This point represents the robot’s

model in the environment and the dimension of con-

ﬁguration space is equal to the number of degrees of

freedom of the mechanical system. Then the algo-

rithm searches a free path for a point in the roadmap.

Figure 3 illustrates the process of generating a proba-

bilistic roadmap for an example occupancy grid map

with 80 random samples.

An extension of the original PRM, which is called

medial axis based PRM (i.e. MAPRM) (Wilmarth

et al., 1999), aims to efﬁciently retract any sampled

conﬁguration, free or not, onto the medial axis of the

free space without having to compute the medial axis

explicitly. This strategy is applied to our approach

with some small modiﬁcations. The implementation

details can be seen in Algorithm 1. When the random

Sampling-basedMulti-robotMotionPlanning

551

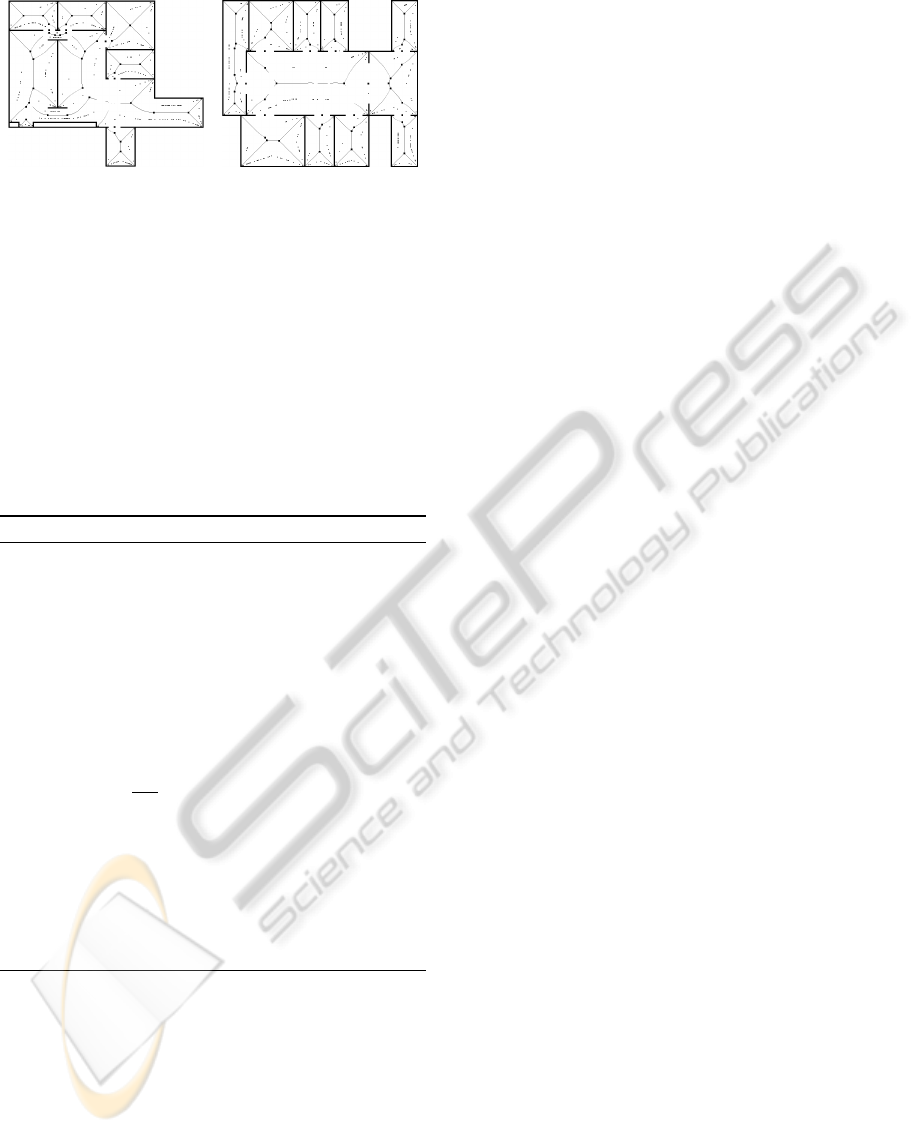
(a) map A (b) map B

Figure 4: The additional waypoints extracted by using the

sampling-based method with 400 random samples.

conﬁguration p is sampled, the nearest obstacle con-

ﬁguration q to p should be found, and another conﬁg-

uration r is set to ﬁx p at the center of q and r. If r is a

free conﬁguration, then p will be moved to their cen-

ter and r will be pushed to a farther location. This step

is repeated until r becomes an obstacle conﬁguration.

The algorithm produces a self adaptive medial axis

synthesis, which is ﬁtted to the clearance of each lo-

cal free space. The results of applying this algorithm

can be seen in Figure 4.

Algorithm 1: Medial axis based PRM.

Require: N, the sufﬁcient number of points to gener-

ate.

Ensure: N points in C

f ree

by sampling on the medial

axis.

1: repeat

2: Generate a uniformly random point p in C.

3: if p ∈ C

f ree

then

4: Find the nearest point q ∈ C

obs

to p.

5: r = 2p − q

6: while r ∈ C and r ∈ C

f ree

7: p =

p+r

8: r = 2p − q

9: end while

10: if r ∈ C

obs

then

11: p is added to the set of medial axis.

12: end if

13: end if

14: until N points have been generated.

3.3 Hungarian Method

The last step is to assign the waypoints to robots by

using the Hungarian method. The Hungarian method

is a combinatorial optimization algorithm which can

solve the assignment problem in polynomial time

(O(n

)). It was developed and published by (Kuhn,

1955). In the context of our research, given n way-

points and n robots, we would like to ﬁnd the best way

(cost minimizing assignment) to assign the waypoints

to the robots. The implementation details on this issue

by using the Hungarian method can be summarized in

the following four steps:

1. Construct a n × n matrix containing the cost of as-

signing each waypoint to a robot. The cost could

be the distance or energy required for the robot to

reach the waypoint.

2. The minimum element in each row is subtracted

from all the elements in that row, and the mini-

mum element in each column is subtracted from

all the elements in that column.

3. Find the minimum number of lines required to

cover all the zeros across rows and columns. If

the number of the lines is n, then the optimal way-

point allocation plan can be given by selecting

a combination from the modiﬁed cost matrix in

such a way that the sum is zero. Otherwise, con-

tinue with Step 4.

4. Find the smallest element which is not covered by

any of the lines. Then subtract it from each ele-

ment which is not covered by the lines and add it

to each element which is covered by a vertical and

a horizontal line. Continue with Step 3.

The implementation of the Hungarian method de-

scribed above requires a square cost matrix, which

means the number of waypoints and the number of

robots should be equal, thus each robot can only move

to a waypoint. On the contrary, if the cost matrix is

not square, then we have to augment it into a square

matrix by adding zero rows or columns. Suppose

there are three robots, r

, r

and r

, and only two way-

points, p

and p

, then the 3 × 3 cost matrix can be

represented as follows:

C =





cost(r

, p

) cost(r

, p

) 0

cost(r

, p

) cost(r

, p

) 0

cost(r

, p

) cost(r

, p

) 0





(3)

Finally we combine the three methods described

above (i.e. the Voronoi diagram, the probabilistic

roadmap and the Hungarian method), and take into

account both the primary waypoints and the addi-

tional waypoints to coordinate multi-robot motion

planning.

4 EXPERIMENTS

4.1 Experimental Setup

Our approach has been implemented and tested in

simulation with the 2D multiple robots simulator

Player/Stage (Gerkey et al., 2003). The experiment

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

552

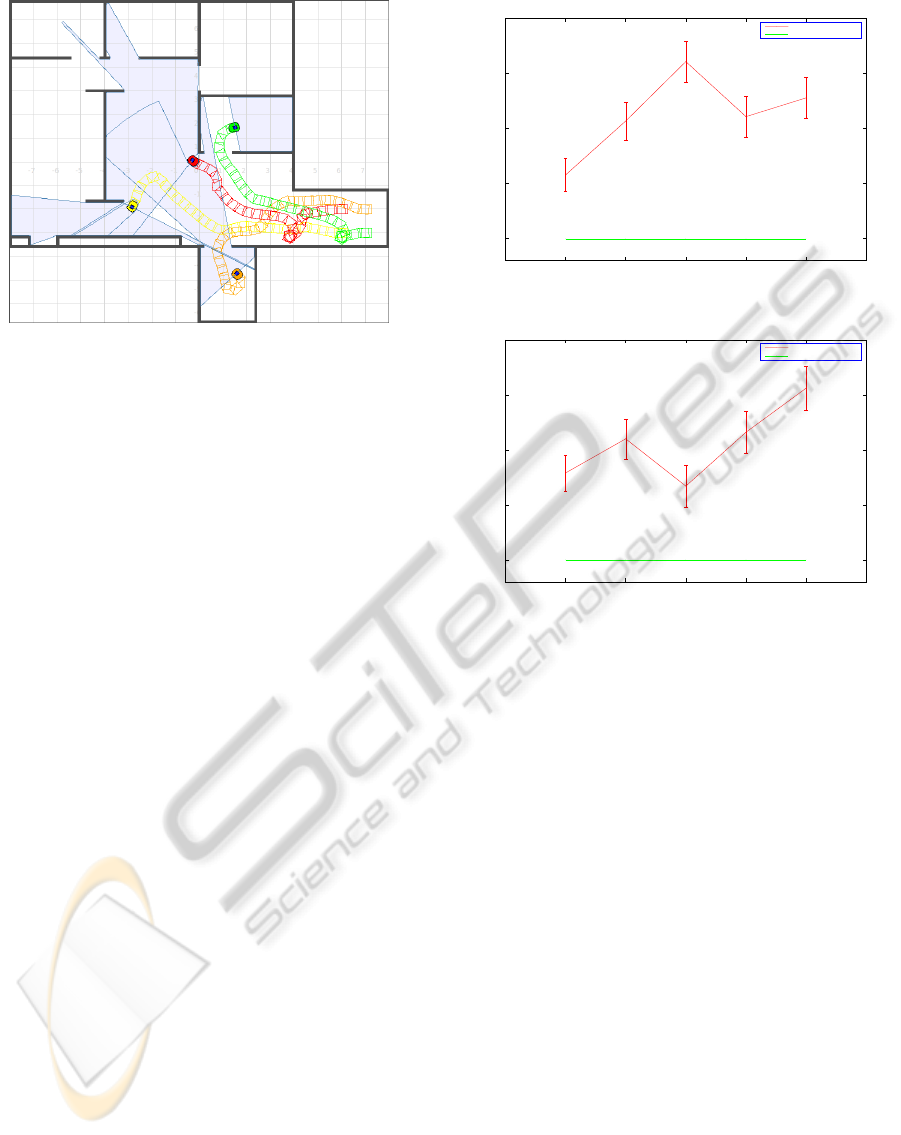
Figure 5: Four robots explore an unknown environment co-

operatively. The green robot and the orange robot are ex-

ploring different rooms. The red robot and the yellow robot

are exploring corridors along different paths.

is to explore an unknown indoor environment by us-

ing a group of virtual Pioneer 2-DX robot equipped

with a laser range ﬁnder which can provide 361 sam-

ples with 180 degrees ﬁeld of view and a maximum

range of 8 meters. Every robot is equipped with

an abstract localization device which models the im-

plementation of SLAM (Simultaneous Localization

And Mapping), and a navigation device which per-

forms the wavefront propagation algorithm (Latombe,

1991) for global path planning and the vector ﬁeld

histogram algorithm (Ulrich and Borenstein, 1998)

for goal seeking and local obstacle avoidance. A cen-

tral planning server is assumed, which is able to com-

municate with all robots and assign the exploration

tasks to each one. In addition, all the robots share an

occupancy grid map with respect to the structure of

the environment during their exploration mission.

A different number of robots (from two to six)

combining with two environments is used to evaluate

our approach. In addition, a comparison with exper-

imental results of our approach and a Voronoi-based

approach is given. Figure 1 ((a) and (b)) depicts two

experimental maps used in our simulation which are

enclosed spaces with 14 meters long and 16 meters

wide. The ratio between real-world time and simula-

tion time is about 1:3. All experiments reported in this

paper were carried out on a system with an Intel Core

2 Duo E8400 3.00GHz processor, an Intel Q43 Ex-

press chipset and two DDR2 800MHz 1024MB dual

channel memory. A screenshot of our implementation

can be seen in Figure 5.

1 2 3 4 5 6 7

exploration time gain [%]

number of robots

map A

Sampling-based

Voronoi-based

(a) map A

1 2 3 4 5 6 7

exploration time gain [%]

number of robots

map B

Sampling-based

Voronoi-based

(b) map B

Figure 6: Exploration time gained by using our sampling-

based approach compared with the Voronoi-based ap-

proach.

4.2 Experimental Results

The results of the experiments are given in Figure

6. We measured the exploration time gained by

our sampling-based approach and compared to the

Voronoi-based approach. In each plot, the abscissa

denotes the team size of the mobile robots, the or-

dinate denotes the time gain in percent of the total

exploration time, and the error bar indicates the con-

ﬁdence interval of each corresponding gain of robot

team size with the 0.95 conﬁdence level. 10 runs are

performed for each team size. Figure 6 shows that an

exploration time saving of 5.8% to 16.1% in map A

and 6.4% to 15.3% in map B is obtainable under our

sampling-based approach compared to the Voronoi-

based approach. These results show that our tech-

nique could improve performance of the multi-robot

motion planning.

We also counted the average number of waypoint

conﬂicts in each experiment map, as shown in Table

1. This table shows that the waypoint conﬂict is obvi-

ously reduced by using our approach compared to the

Sampling-basedMulti-robotMotionPlanning

553

Table 1: The Number of Waypoint Conﬂicts by Using Our

Sampling-based Approach Compared with The Voronoi-

based Approach

(a) map A

# robots 2 3 4 5 6

Sampling-based 2.5 2.9 4.3 3.1 3.4

Voronoi-based 6.2 6.7 11.6 8.1 10.2

(b) map B

# robots 2 3 4 5 6

Sampling-based 0.0 1.4 2.7 2.9 2.4

Voronoi-based 4.1 6.2 6.4 7.7 10.7

Voronoi-based approach. For this reason, the problem

of waiting situation such as collision, congestion and

deadlock has been alleviated and the system perfor-

mance is improved.

5 CONCLUSIONS

In this paper, we presented a multi-robot motion plan-

ning approach based on sampling method. This ap-

proach is designed to relieve multi-robot waiting situ-

ation problem such as collision, congestion and dead-

lock, by increasing the number of waypoints for mo-

bile robots. The proposed approach includes three

main steps: the ﬁrst step is to identify primary way-

points on top of an occupancy grid map by using the

Voronoi diagram, the second step is to generate ad-

ditional waypoints on top of the Voronoi diagram by

using the sampling-based method, and the third step

is to assign the waypoints to robots by using the Hun-

garian method. The efﬁciency of our approach was

veriﬁed by simulation and experimental results.

REFERENCES

Bennewitz, M., Burgard, W., and Thrun, S. (2001). Op-

timizing schedules for prioritized path planning of

multi-robot systems. In Proceedings of ICRA’01,

pages 271–276, Seoul, Korea.

Gerkey, B. P., Vaughan, R. T., and Howard, A. (2003). The

Player/Stage project: Tools for multi-robot and dis-

tributed sensor systems. In Proceedings of ICAR’03,

pages 317–323, Coimbra, Portugal.

Guo, Y. and Parker, L. E. (2002). A distributed and optimal

motion planning approach for multiple mobile robots.

In Proceedings of ICRA’02, pages 2612–2619, Wash-

ington, DC, USA.

Hazon, N., Mieli, F., and Kaminka, G. A. (2006). Towards

robust on-line multi-robot coverage. In Proceedings

of ICRA’06, pages 1710–1715, Orlando, FL, USA.

ager, M. and Nebel, B. (2001). Decentralized collision

avoidance, deadlock detection, and deadlock resolu-

tion for multiple mobile robots. In Proceedings of

IROS’01, pages 1213–1219, Maui, HI, USA.

Kavraki, L. E., Kolountzakis, M. N., and Latombe, J.-C.

(1996). Analysis of probabilistic roadmaps for path

planning. In Proceedings of ICRA’96, pages 3020–

3025, Minneapolis, MN, USA.

Kuhn, H. W. (1955). The hungarian method for the assign-

ment problem. Naval Research Logistics Quarterly,

2(1):83–97.

Latombe, J.-C. (1991). Robot Motion Planning. Kluwer

Academic Publishers.

Luna, R. and Bekris, K. E. (2011). Efﬁcient and complete

centralized multi-robot path planning. In Proceedings

of IROS’11, pages 3268–3275, San Francisco, CA,

USA.

Luo, C., Yang, S. X., and Stacey, D. A. (2003). Real-

time path planning with deadlock avoidance of multi-

ple cleaning robots. In Proceedings of ICRA’03, pages

4080–4085, Taipei, Taiwan.

Marcolino, L. S. and Chaimowicz, L. (2009a). Trafﬁc

control for a swarm of robots: Avoiding group con-

ﬂicts. In Proceedings of IROS’09, pages 1949–1954,

St. Louis, MO, USA.

Marcolino, L. S. and Chaimowicz, L. (2009b). Trafﬁc con-

trol for a swarm of robots: Avoiding target conges-

tion. In Proceedings of IROS’09, pages 1955–1961,

St. Louis, MO, USA.

Svestka, P. and Overmars, M. H. (1995). Coordinated mo-

tion planning for multiple car-like robots using prob-

abilistic roadmaps. In Proceedings of ICRA’95, pages

1631–1636, Nagoya, Japan.

Tanner, H. G. and Kumar, A. (2005). Towards decentraliza-

tion of multi-robot navigation functions. In Proceed-

ings of ICRA’05, pages 4132–4137, Barcelona, Spain.

Thrun, S. (1998). Learning metric-topological maps for in-

door mobile robot navigation. Artiﬁcial Intelligence,

99(1):21–71.

Ulrich, I. and Borenstein, J. (1998). VFH+: Reliable obsta-

cle avoidance for fast mobile robots. In Proceedings

of ICRA’98, pages 1572–1577, Leuven, Belgium.

Wilmarth, S. A., Amatoy, N. M., and Stiller, P. F. (1999).

MAPRM: A probabilistic roadmap planner with sam-

pling on the medial axis of the free space. In Pro-

ceedings of ICRA’99, pages 1024–1031, Detroit, MI,

USA.

Wurm, K. M., Stachniss, C., and Burgard, W. (2008). Coor-

dinated multi-robot exploration using a segmentation

of the environment. In Proceedings of IROS’08, pages

1160–1165, Nice, France.

Zivkovic, Z., Bakker, B., and Kr

ose, B. (2006). Hierarchi-

cal map building and planning based on graph parti-

tioning. In Proceedings of ICRA’06, pages 803–809,

Orlando, FL, USA.

ICINCO2013-10thInternationalConferenceonInformaticsinControl,AutomationandRobotics

554