Emergency Ambulance Deployment in Val-de-Marne Department

A Simulation-based Iterative Approach

Lina Aboueljinane, Evren Sahin and Zied Jemai

Ecole Centrale Paris, Grande voie des Vignes, 92295 Chatenay-Malabry, France

Keywords: Emergency Medical Services, Ambulance Deployment, Discrete Event Simulation, Healthcare, Operations

Management.

Abstract: The French Emergency Medical services, known as SAMU, are public safety systems responsible for the

coordination of pre-hospital care under emergency conditions throughout a given geographic region. The

goal of such systems is to respond timely and adequately to population calls by providing first aid services

and transferring patients, when needed, to the appropriate care facility. In this paper, we propose a multi-

period version of the Maximum Expected Covering Location Problem applied to the case of the SAMU 94

responsible for the Val-de-Marne department (France). The assumption that the busy fractions are identical

for all demand points is relaxed by adopting an iterative method to compute a priori estimates of these

parameters in the model using an ARENA discrete-event simulation model of the SAMU 94. The solutions

obtained from the mathematical model are then assessed by simulation regarding the time required to

respond to an emergency call by getting to the patient location, known as response time, which is a critical

aspect for the SAMU providers. Experimental results showed that the proposed method increased average

percentage of most serious calls responded to within the target time of 15 minutes up to 15% compared to

the current system performance.

1 INTRODUCTION

Pre-hospital care refers to first aid services provided

to patients under emergency conditions from

incident reporting, i.e. an incoming call via an

emergency number, to definitive care, involving

facilities, equipment and personnel trained to

provide phone support, stabilization of patient’s

condition and transportation to an appropriate care

facility. In France, the emergency medical service

(EMS) system responsible for providing such

services is known as the SAMU system which

stands for the French acronym of “Urgent Medical

Aid Service”. It was established in 1968 to

coordinate the activity of the “Mobile Emergency

and Resuscitation Services”, named SMUR teams,

which are mobile response vehicles staffed with

qualified personnel and operated by public hospitals.

The SAMU rescue process is organized according to

two types of operations: Central operations,

performed in a reception and regulation (R&R)

centre, that aim to provide phone support and to

decide the proper response for each call received

depending on its degree of urgency, and External

operations that aim at sending one or several SMUR

team(s) to perform pre-hospital care for two types of

rescues: primary rescues which are related to major

injuries or illnesses that require immediate medical

assistance outside of the hospital (e.g., cardiac arrest,

trauma, childbirth...) and secondary rescues which

correspond to the transport of patients from one

hospital to another, in case medical staff assistance

is needed during the transfer. Between rescues,

SMUR teams are placed in fixed positions, called

bases that are currently located in public hospitals.

The SAMU system is managed at a department level

(i.e. a French administrative division corresponding

to a median area of about 6 000 km²) in order to

provide a 24-hour service for each department.

One of the critical performance measures for the

SAMU providers, particularly in case of life-

threatening emergencies, is the response time,

defined as the period between the receipt of a call

and the first arrival of a SMUR team at the scene of

incident. Several authors observed the association

between low response time and high survival rate of

patients (Cummins, 1989); (Vukmir, 2006); (White

et al., 1996). Hence, having a high coverage, i.e.

565

Aboueljinane L., Sahin E. and Jemai Z..

Emergency Ambulance Deployment in Val-de-Marne Department - A Simulation-based Iterative Approach.

DOI: 10.5220/0004623105650576

In Proceedings of the 3rd International Conference on Simulation and Modeling Methodologies, Technologies and Applications (HA-2013), pages

565-576

ISBN: 978-989-8565-69-3

 2013 SCITEPRESS (Science and Technology Publications, Lda.)

percentage of calls responded to within a specific

bound, is a commonly expressed objective for the

SAMU managers. Another concern of the SAMU

system is to reduce the significant expense involved

in its management, including capital (acquisition of

physical plant, vehicles, equipment, communication

etc.) and operating costs (salaries, training,

maintenance, etc.).

Both timeliness and economical goals can be

achieved through the optimization of several design

and operation decisions that are highly interrelated

and may be classified according to the following

classical operations management hierarchical

decision framework:

 Long term decisions such as setting service level

objectives, identifying the location and the

capacity of the fixed facilities needed to perform

central operations as well as a set of potential

locations for SMUR teams bases throughout the

covered department ;

 Mid-term decisions: such as allocating SMUR

teams to bases selected among those specified in

the long term level so as to ensure a brief delay in

reaching every call location (known as the

deployment problem) and scheduling shifts for

human resources;

 Short-term decisions: such as determining the rules

of assigning one or several available SMUR teams

to a call (known as the dispatching problem),

allocating SMUR teams to bases in order to

improve coverage of future requests under

temporal and geographical fluctuations of demand

pattern (known as Multi-period redeployment) or

depending on the number of SMUR teams

available following the allocation or release of a

team (known as dynamic redeployment);

In literature, several operations research tools have

been used to improve the performance of EMS

systems through the optimization of these decisions.

The current research addresses the multi-period

redeployment problem as an improvement

opportunity to develop service coverage

performances of the SAMU system in the Val-de-

Marne department (south east of the city of Paris),

named SAMU-94, under limited number of

resources. In this regard, we propose an iterative

method that combines the use of a probabilistic

mathematical covering model to find the optimal

locations of the existing SMUR teams throughout

the service area for different periods of time, with

the use of a discrete-event simulation model of the

system, implemented in ARENA software, in order

to evaluate the busy fraction parameter (i.e. the

probability for a SMUR team of being unavailable to

answer a call) required to solve the analytical model

as well as to analyze the performance of the system

under the redeployment solutions obtained from this

model.

The paper is organized as follows: Section 2

briefly describes the literature review on the use of

simulation and mathematical models in EMS

management. Section 3 describes the detailed

methodology used to build the SAMU-94 simulation

model, including the process description, the data

collection and the validation of the initial

configuration of the model. In Section 4, we present

the probabilistic covering model and the iterative

approach to estimate the busy fraction parameters.

Experimental results are described in Section 5.

Finally, Section 6 provides conclusions and presents

some directions for future research.

2 LITERATURE REVIEW

In literature, mathematical programming is one of

the most studied analytical tools used to improve the

performance of EMS systems. Mathematical models

have been focused mainly on the decision of

assigning rescue teams to bases, in both mid-term

(deployment problem) and short term (dynamic and

multi-period redeployment) settings. Research on

this area has been largely derived from two early

deterministic models: The Location Set Covering

Problem (LSCP), developed by (Toregas et al.,

1971), which aims to minimize the number of rescue

teams needed to cover all demand points within a

target distance (time), and the Maximal Covering

Location Problem (MCLP), proposed by (Church

and ReVelle, 1974), which maximizes the

population coverage within a target distance (time)

using a limited number of available rescue teams.

These two basic models overestimate coverage since

they ignore some stochastic aspects such as the fact

that dispatched rescue teams become unavailable to

answer incoming calls. Two extensions have

therefore been proposed to provide more robust

location solutions. One extension is to consider the

deterministic covering problem with an extra

coverage, i.e. to maximize the demand covered by

more than one rescue team to serve simultaneous or

close calls (Daskin and Stern, 1981); (Eaton et al.,

1986); (Gendreau et al., 1997); (Hogan and ReVelle,

1986). The other extension consists of probabilistic

models that explicitly consider rescue teams’

potential unavailability through the use of the busy

fraction parameter. These models include the

expected covering location models that aim to

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

566

maximize the expected demand covered, expressed

as a function of the busy fraction, such as the

MEXCLP (Maximum Expected Covering Location

Problem) of (Daskin, 1983) and its applications and

extensions (Bianchi and Church, 1988); (Fujiwara et

al., 1987); (Goldberg et al., 1990b); (Repede and

Bernardo, 1994). Another probabilistic approach

consists of the formulation of the deployment

problem as a chance constrained stochastic program

that incorporates the unavailability aspect as a linear

constraint. This constraint uses the busy fraction to

compute a lower bound of rescue teams required to

achieve a given reliability level α in serving each

demand point (ReVelle and Hogan, 1989); (ReVelle

and Marianov, 1991). These models typically

assumed that all rescue teams operate independently

and have the same busy fraction q, estimated by

dividing their total workload by their total operating

time, regardless of their location and the overall

number of teams servicing each demand point.

These assumptions are obviously not valid since the

team’s location affect the travel time to the call

location and therefore the total workload. Moreover,

the larger is the fleet size covering an area, the lower

is the probability of a team to be busy. The difficulty

of estimating the busy fraction parameters which are

related to the location of teams is that this location is

precisely the solution obtained from the optimization

model, while the latter requires these parameters to

be known a priori in order to provide a solution.

Yet, for a specific deployment plan, several authors

used descriptive tools such as hypercube queuing

models (Batta et al., 1989); (Larson, 1974);

(Marianov and Revelle, 1994) and computer

simulation (Ingolfsson et al., 2003); (Su and Shih,

2003) to pre-compute more accurate estimations of

these parameters.

Apart from the mathematical programming

approach mentioned above, computer simulation has

been one of the most widely used technique to

identify potential areas of improvement in EMS

systems without considering simplifying

assumptions needed to solve analytical models.

Indeed, the main advantage of simulation in dealing

with such problems is its ability to describe the

system in a high degree of detail, to estimate several

performance measure predictions and to handle

several sources of uncertainty such as time-

dependent arrival rate and location of calls, available

capacity and location of rescue teams, duration of

service time depending upon the medical needs of

patient and bed availability of definitive care

facilities. Research that is available in this area may

be classified into two groups:

 Simulation models used to estimate the impact of

several scenarios (i.e. changes applied to

simulation model assumptions, algorithms and/or

data) on some selected performance outputs.

 Simulation models primarily developed to assess

the performance of solutions that are obtained

from analytical models in a more realistic

framework

The scenarios considered in the first group are

typically related to the design and operation

decisions described in Section 1. The most explored

long term decisions related scenarios consist of

adding more rescue teams or new potential bases.

These two scenarios are usually explored

concurrently to be compared in terms of cost and

quality performance (Gunes and Szechtman, 2005);

(Inakawa et al., 2010); (Ingolfsson et al., 2003);

(Savas, 1969). Another scenario tested consists of

assessing the effect of an increase in demand

following for instance the growth of population or

the enlargement of the scope of EMS system

(Lubicz and Mielczarek, 1987); (Silva and Pinto,

2010). As for the mid-term decisions related

scenarios considered in EMS literature, they mainly

focused on the deployment problem which is usually

evaluated jointly with the long term scenario of

considering new potential bases in order to assess

the relocation of rescue teams close to high demand

areas (Fitzsimmons, 1971); (Goldberg et al., 1990a);

(Henderson and Mason, 2005). Finally, the available

literature in the area of short term decisions related

scenarios addresses changes either in dispatching

rules (Koch and Weigl, 2003); (Su and Shih, 2003),

destination hospital assignment policies (Wang et

al., 2012); (Wears and Winton, 1993), multi-period

redeployment strategy (Peleg and Pliskin, 2004),

dynamic redeployment strategy (Ingolfsson et al.,

200)3; (van Buuren et al., 2012) and travel speeds of

emergency vehicles (Aringhieri et al., 2007); (Liu

and Lee, 1988).

The second use of simulation with analytical

models has also largely been adopted in EMS

literature. Typically, this combined approach

involves using a location or a relocation

mathematical programming model first, in order to

determine sets of optimal locations, given the set of

feasible locations, and then using simulation to

estimate system performance under the resulting

deployment/redeployment plan. In the literature, the

mathematical programming models proposed in such

approach include deterministic models with simple

coverage (Berlin and Liebman, 1974); (Uyeno and

Seeberg, 1984), deterministic models with multiple

coverage (Aringhieri et al., 2007) and probabilistic

EmergencyAmbulanceDeploymentinVal-de-MarneDepartment-ASimulation-basedIterativeApproach

567

models (Fujiwara et al., 1987); (Harewood, 2002);

(Repede and Bernardo, 1994).

In this paper, we propose to apply this combined

approach to the EMS of Val-de-Marne department

(SAMU-94) in order to improve the response time

performance of the system. For this purpose, we

proposed a multi-period extension of the MEXCLP

(Daskin, 1983) that integrates some specificities

related to call priorities as well as site-specific busy

fraction parameters depending on the number of

rescue teams serving each site and the time period.

Busy fraction parameters are estimated using an

iterative method, derived from (Lee et al., 2012),

that uses a discrete event simulation model of the

system in each step to update the busy fraction

estimates based on the location solution obtained

from the optimization model in the previous step.

The updated estimates are subsequently used in the

optimization model to provide updated location

solution. This iterative process continues until the

location solution converges.

3 SIMULATION MODEL

3.1 Problem Description

This simulation study used the discrete event

simulation software ARENA (Rockwell

Automation, Milwaukee, Wisconsin) to build a

model that takes the SAMU 94 system as its subject

and seeks to compute credible estimates of busy

fraction and response time performance measures. A

first step in the methodology of performing the study

consists of conducting meetings and interviews with

the SAMU-94 experts in order to clarify the input

parameters and the detailed process associated with

the system which involves various types of human

and material resources which are:

 Operators: Located in the R&R centre, they are

responsible for answering calls, identifying

inappropriate calls, creating a medical file and

recording the basic information relative to the

nature of the request;

 Regulators: Located in the R&R centre, they are

responsible for performing medical evaluation of

calls and deciding on the best solution for the

patient. There are two types of regulators:

emergency physicians, named “SAMU regulators”,

responsible for high priority calls, and general

practitioners, named “PDS regulators”, responsible

for remaining calls;

 SMUR teams: consisting of a vehicle staffed by

one physician, one driver, one nurse and/or one

emergency medical technician. There are two

types of vehicles: well-equipped ambulances,

called Mobile Intensive Care Units (MICU), and

medical vehicles (MV) which are usually

dispatched for the most serious calls because they

are faster than MICU but do not allow for the

transport of the patient. The SMUR teams are

currently located in two bases: one central base

located at Henri-Mondor Hospital (HM) and one

auxiliary base located in Villeneuve-Saint-Georges

Hospital (VSG);

 Rescue physician: an emergency physician who

can either operate as a SAMU regulator or as a

physician in a SMUR team.

The SAMU-94 central operations are triggered when

a call is first received by an operator in the R&R

centre which is located in the central base HM.

Depending on the potential severity of the call, the

operator chooses to redirect the call to a SAMU or a

PDS regulator. The regulator performs a medical

evaluation which can lead to several possible

decisions: In the case of primary rescues, if the call

is not urgent, a simple advice is given to the patient

or a private ambulance is dispatched. If the request

is a relative emergency, the call is transferred to a

basic life support or BLS system such as fire-

fighters or red-cross. However, if the incident turns

out to be more urgent than the first evaluation, the

BLS calls back an operator to ask for the dispatch of

a SMUR team. These calls are referred to as primary

rescues with sending BLS as first effector.

Otherwise, if the request is an absolute emergency, a

SMUR team is immediately dispatched to the call

location, which is known as primary rescues with

sending SMUR team as first effector.

In the case of a secondary call, an appointment is

taken with the origin hospital in order to send a

SMUR team when more than one team is available

in the central station.

Once the regulator decides to send a SMUR

team, he evaluates the availability and the

geographical location of the fleet and notifies the

closest available unit. This is the beginning of

external operations. The interval between the arrival

of the call until a SMUR team is notified is referred

to as the dispatching time. The selected rescue team

prepares the rescue by gathering any necessary

equipment that may not be available on the vehicle,

inquiring information concerning the incident and

rushing to the vehicle. The interval between the time

the SMUR team receives the notification to the time

it leaves for rescue is called preparation time. Note

that this step is only performed if the SMUR team is

located at a base when notified of a call. The SMUR

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

568

team then leaves for rescue. The travel time is the

time elapsed from the initial movement of the

vehicle until the arrival at the scene.

The SMUR team spends some time to stabilize

the patient. If more advanced care is deemed

necessary, the SAMU regulator determines the

appropriate destination hospital and communicates

this decision to the SMUR team. The choice of a

primary rescue’ destination hospital may depend on

several factors such as the proximity of hospital, its

available capacity and appropriate facilities for the

patient (specialists, particular equipment...) or

patient choice. The SMUR team therefore prepares

the patient for transportation and leaves the scene.

The interval between the time the rescue team

arrives at the scene and the time it leaves is usually

called on-site time. Before the transport to the

destination hospital, the patient may need a

diagnostic or therapeutic radiography (DTR) such as

MRI, X-ray (if the destination hospital does not have

the appropriate equipment or have long waiting

times). In this case, the SMUR team takes the patient

to the medical service where the DTR is performed.

The time interval between the SMUR team arrives at

the DTR medical service and the time it leaves is

called diagnostic or therapeutic radiography time.

After arriving at the destination hospital, the rescue

team transfers the patient to the hospital staff and

spends some time completing paperwork. The time

needed to perform these tasks is called drop-off time.

Finally, the SMUR team becomes available and can

travel for another rescue or return to the base to

which it is assigned to wait for the next mission.

3.2 Data Collection and Analysis

The rescue records of the SAMU 94 were collected

for a period of 15 months of operations. This

database, hereafter referred to as “regulation

database”, included for each call the following data:

(1) The time and date of each call; (2) The origin of

the call; (3) The type of call (primary/secondary);

(4) The first effector if primary call (SMUR team or

BLS); (5) The priorities assigned to the call, by the

regulator and by the SMUR team once at call

location. Priority 1 is assigned to life-threatening

emergencies (e.g. cardiac arrests, serious trauma,

etc.) and priority 2 is assigned otherwise; (6) The

response team that performs the rescue; (7) The

destination hospital; (8) The timing of the different

steps in the rescue process: SMUR team notified,

SMUR team leaves for the rescue, SMUR team

arrives at the scene, SMUR team leaves the scene,

SMUR team arrives at the diagnostic or therapeutic

radiography service, SMUR team leaves the

diagnostic or therapeutic radiography service,

SMUR team arrives at the hospital, SMUR team

finishes the rescue.

This database was first analysed to exclude any

record (call) containing missing data or errors in

measures. Only 2.1% of the logged calls were

therefore removed, resulting in a database of 9836

calls.

From the verified records, we extracted the

empirical distributions of the following:

 The arrival rate of calls per hour of the day, day of

the week and type of call (primary/secondary);

 The priority of each type of call: These priorities

are used in the developed simulation model to

establish a hierarchy in responding to simultaneous

calls or calls waiting for the dispatch of a SMUR

team;

 The first effector (SMUR team or BLS) for

primary calls;

 The location of calls and hospitals: In order to

accurately model this geographical distribution, we

aggregated the network road nodes based on their

proximity in a zone structure corresponding to

basic units of approximately 2000 residents,

developed by the French National Institute for

Statistics and Economic Studies (INSEE) and

known as “IRIS” for the French acronym of

“aggregated units for statistical information”. The

Val-de Marne department is composed of 527

IRIS. This division is a reasonable computational

trade-off that aggregate the large amount of calls

into small areas without having a significant travel

time within a given area;

 The processing times per type and priority of calls:

These times include the dispatching time, the

preparation time, the on-site time, the diagnostic or

therapeutic radiography time and the drop-off time

for primary rescues. As for secondary rescues, they

are considered as low priority calls which aim to

provide transport of patient when possible without

timeliness constraints. Therefore they were

implemented in the model as an aggregated service

time so as to properly size the utilization rate of

resources ;

The historical data were first fitted to theoretical

distributions, using Kolmogorov-Smirnov and Chi-

Square goodness-of-fit tests, which provided low p-

values (less than 0.05). Therefore, we chose to use

the empirical distributions that allow to better

capture the characteristics of the data (Kelton et al.,

2008).

Unlike processing times, there are no empirical

travel times’ data available for currently unexplored

EmergencyAmbulanceDeploymentinVal-de-MarneDepartment-ASimulation-basedIterativeApproach

569

road networks due to different deployment

strategies. Hence, in cooperation with the National

Geographic Institute (IGN), we used a shortest path

algorithm to pre-compute travel times for every

possible origin, destination, time period and priority

of call. The origins and destinations correspond to

the 527 IRIS of the service area that include all

demand points, bases and hospitals. The time

periods represent the degree of traffic load at various

times of the day according to six shifts that

distinguish between weekdays (6:00-10:00, 10:00-

15:00, 15:00-21:00 and 21:00-6:00) and weekends

(12:00-21:00 and 21:00-12:00). Based on the GPS

traces database of the SAMU-94 vehicles, an

average travel time per time period was assigned to

each section of the road network of the Val-de-

Marne department according to its typology

(motorway, main road, minor road, local street). For

any given combination of origin IRIS, destination

IRIS and time period, a sample of 10 pairs of exact

addresses were randomly chosen within the two

IRIS. For each pair, travel time was computed by

summing up the average travel times associated with

the sections that form the shortest path between the

two addresses. The average of the 10 pairs’ travel

times provided a good approximation of the

combination travel time compared to the common

assumption of computing travel times between the

centres of the zones. Finally, as SMUR teams are

allowed to travel at all possible speed when

responding to primary calls of priority 1, related

travel times were weighted by a multiplicative factor

estimated at 0.937 to decrease them compared to

standard travel times.

3.3 Simulation Model Implementation

and Validation

The previously described SAMU-94 rescue process

and data were summarized in a computerized model

implemented using ARENA. The outcome variables

of the model included the response time of each

priority/effector of primary calls and the utilization

rates of each SMUR team for each time

period/priority. Different random number seeds were

used to replicate the model 20 times. Each

replication length corresponds to 15 months of

operations and 1 day as a warm up period.

We performed a historical data validation by

comparing the system’s empirical data to the

corresponding simulation-derived distribution. An

example of response time measure validation for

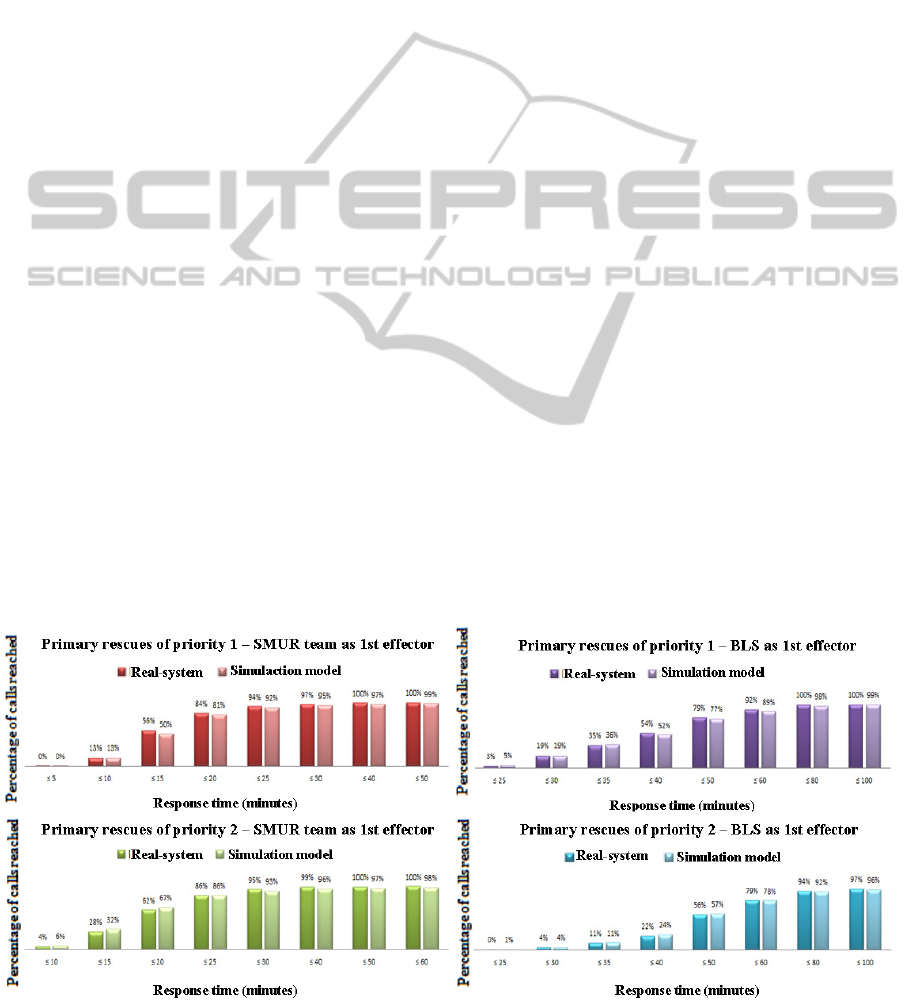
primary rescues, shown in Figure 1, indicates that

model’s outputs are quite close to the observed

distributions as the differences do not exceed 5.7%.

4 OPTIMISATION MODEL

In order to optimally locate SMUR teams close to

primary demand so as to improve the corresponding

response time performance, we propose the use of a

probabilistic multi-period model that seeks to

maximize the expected primary demand covered

using a limited number of SMUR teams. The model,

which is derived from the Maximum Expected

Covering Location Problem (MEXCLP) of (Daskin,

1983), is as follows:

 







1

















∈∈∈

(1)

Figure 1: The cumulative distributions of real and simulated response time for primary rescues.

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

570

Subject to











  



∈









∈







∈







∈



(2)





∈









∈



(3)





∈ 



∈







∈



(4)





∈



0,1







∈,1,………..,



,

∈,∈



(5)

Set of Index

V is the set of all demand nodes.

W is the set of all potential bases.

T is the set of all periods of time.

P is the set of primary calls’ priorities.

Parameters

ijt

is the travel time from the base j to the demand

point i during the period t.

pit

= {j∈W : r

ijt

≤ S

} is the set of all potential bases

eligible to serve calls of priority p located in the

demand node i within a target travel time S

itp

is the total number of calls of priority p received

in the period t associated with the demand node i.

is the number of SMUR teams scheduled in the

time period t.

is the weight associated with the priority p

demand coverage.

ikpt

is the average busy fraction of k SMUR teams

eligible to serve demand of priority p located at node

i during the time period t.

Decision variables

is an integer variable that corresponds to the

number of SMUR teams assigned to the base j

during the time period t.

ikpt

is a binary variable equal to 1 if demand of

priority p located in demand node i is covered by at

least k SMUR teams during time period t.

The objective function (1) aims to maximize the

total expected demand covered over all nodes and all

time periods. The weight





assigned to priority p

demand allows emphasizing the importance of high-

priority demand coverage and balancing the effect of

a more restrictive target travel time for high priority

calls. Constraint (2) ensures that for each time

period, a demand of priority p located in node i is

assigned to base j only if a team is located at j.

Constraint (3) restricts the number of SMUR teams

to be located to their scheduled capacity per time

period.

For the application of the model, 47 locations

corresponding to the centre of the 47 districts of the

Val-de-Marne department were selected as potential

bases. The 527 IRIS of the department were

considered as demand nodes. There are between 3

and 5 available SMUR teams during weekdays and 3

SMUR teams during weekends. Ten periods of time

were chosen corresponding to the six travel time

periods described in section 3.2 which are

subdivided whenever a change in the scheduled

number of SMUR teams occurs within a given travel

time period. The model was solved using different

weights (α

,α

)={(1,0); (0.75,0.25); (0.5,0.5)} and

different target travel times in minutes

)={(5,10); (10,10); (10,15)}. For each target

travel time, the vector of nodes that can cover each

demand of a given priority at a time period W

pit

was

computed.

The probability that a randomly selected SMUR

team is busy is estimated using the following

equation:







∑







∈













∈,1,…,



,∈,

∈,



  

(6)

where T





is the average amount of time

worked to serve demand of priority p in time period

t by all SMUR teams located at base j∈W





, T





corresponds to the total work time available at

period t for each SMUR team and k is the total

number of SMUR teams located at bases in





. In

case the number of SMUR teams located within S

different from k, we used the mean of the existing

estimates over the set of demand nodes to

approximate the busy fraction parameter, i.e. (6) is

replaced by:







∑



∈









∈,1,…,



,∈

, ∈ ,    ∈ :



  



(7)

We intuitively believe that this assumption will

provide good estimates for





that will avoid any

excessive underestimation or overestimation of the

ability of the system to cover a demand node under a

given number of vehicles, which will lead to fast

convergence of the iterative method.

We then apply the iterative method described in

(Lee et al., 2012) that consists of using the integer

program to obtain optimal location solution for a

given estimation of q



and then running the

simulation model with the obtained location solution

to tune the estimates of q



using (6) and (7). The

initial values of q





were computed based on the

"initial scenario” model that represents the current

SAMU-94 system. Using this initial estimation, the

integer program is solved to provide the optimal

EmergencyAmbulanceDeploymentinVal-de-MarneDepartment-ASimulation-basedIterativeApproach

571

location solution (y









 , which is in turn used

as an input in the simulation model. The resulting

simulated service time worked allows updating the

estimates of q





for the next iteration. This process

is repeated until the location solution converges, i.e.

remains the same for two successive rounds of

iterations, i.e. (y



∗



∗

y



















y









.



For each value of weight/target travel time

parameters, the model has been solved at each

iteration using CPLEX 12.5 on an Intel Core i3, at

2,30 GHz, with 4Go of RAM memory. Solution

times ranged from 3.2 to 9.7 minutes. The obtained

redeployment solution was then fed in the simulation

model and run for twenty 15 months-replications in

order to re-compute the corresponding busy

fractions per time period and priority of calls.

5 EXPERIMENTAL RESULTS

As the purpose of this study is to achieve a

substantial improvement in response time

performance for primary rescues with SMUR team

as first effector, the percentage of calls responded to

within target times of 15 minutes and 20 minutes

were set as the main performance measures used to

compare simulation results for priority 1 and 2

respectively. The optimal redeployment policies

resulting from the alternatives of weight/target travel

time combination, described in Table 1, were

analysed in sequence.

We were first interested in analysing how the

system performances behave through the steps of the

iterative method. In all eight tested alternatives, the

method converged within few iterations ranged from

4 to 7. Examples of the expected coverage

performances obtained from the optimization model

and the response time performances obtained from

the simulation model for each iteration step of

alternatives 1 to 3 are shown in Figure 2. The green

Table 1: Description of the alternatives.

Alternatives

Alt. 1 5 10 0.5 0.5

Alt. 2

5 10 0.75 0.25

Alt. 3

5 10 1 0

Alt. 4

10 10 0.5 0.5

Alt. 5

10 10 0.75 0.25

Alt. 6

10 15 0.5 0.5

Alt. 7

10 15 0.75 0.25

Alt. 8

10 15 1 0

boxes show the 95% confidence interval for the

percentage of calls responded to within the target

response time metric, and the whiskers show the best

and worst cases of the 20 independent runs of each

alternative. As illustrated in the figure, the larger

marginal differences in performances are achieved

between the initial scenario (iteration 0) and iteration

1 solution, achieving an absolute difference of

14,8% ± 0,3% and 9,3% ± 0,2% in the simulated

percentage of calls responded to within the target

response time for priority 1 and 2 respectively. The

results obtained from the subsequent iterations

showed no significant marginal differences that do

not exceed 0,9% ± 0,3% in the percentage of calls

reached within the target response time for both

priorities.

Now we examine the iterative method solution

quality by comparing the converging points’

performances of all the eight alternatives with each

other and with the initial scenario model (See Table

2). The converging redeployment solution

performances obtained from the optimization model

indicated that the expected coverage of priority 1

rescues could be improved by increasing the value

of the weight α

. This improvement is more

significant for low values of target times and

achieved up to 13%, while the corresponding

priority 2 expected coverage showed either a slight

or no decrease. This was however not supported by

the simulation framework. Indeed, simulation results

showed that fair coverage weights for both priority 1

and 2 rescues, associated with small target times

seem to significantly positively impact the response

time performance. Thus, implementing the

redeployment policy resulting from alternative 1

improved the percentage of calls responded to within

15 and 20 minutes by 15,0% ± 0,3% and 9,1% ±

0,1% for priority 1 and 2 respectively when

compared to the current SAMU-94 performances,

which represents an average relative improvement of

29,7% and 13,7%.

Differences between the simulation

performances and the optimization model coverage

seem to derive from the fact that the latter ignores

several aspects. First, a part of primary demand may

be served by the rescue physician who is necessarily

located in HM base since he also operates as a

SAMU regulator in the R&R centre. Thus, the

location of this resource cannot be considered as a

decision variable in the linear program, but yet

affects the response time performance in the

simulation model. Second, unlike the simulation

model, the temporal dimension of the arrival rate as

well as the service time distribution are ignored in

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

572

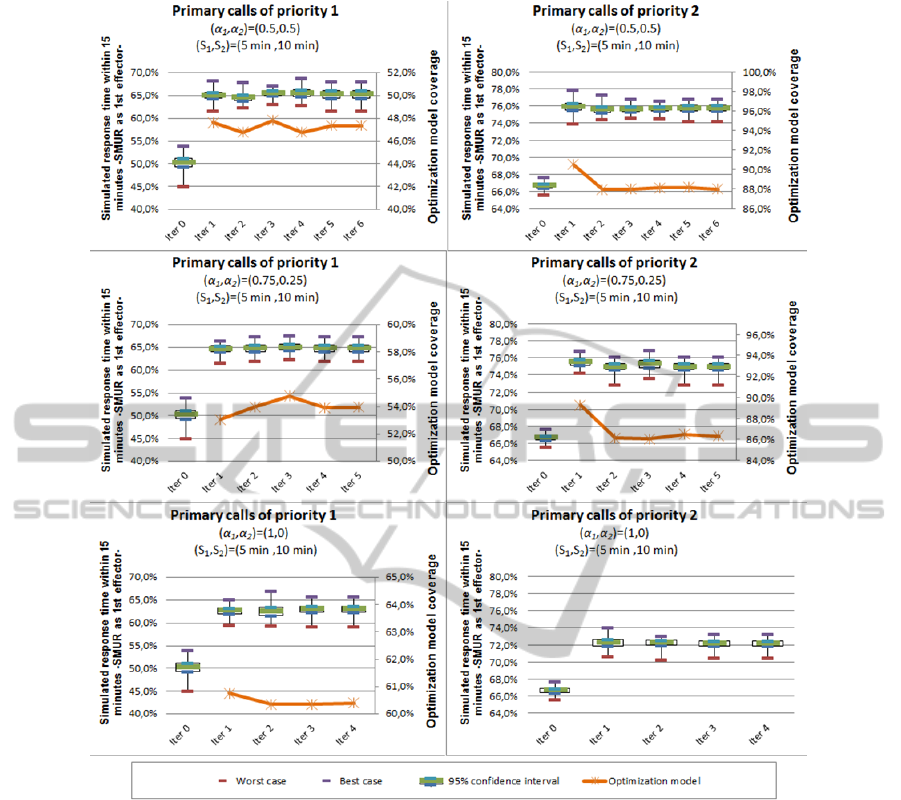
Figure 2: Iterative method performance measures for the (S1,S2)=(5min,10min) alternatives.

model, the temporal dimension of the arrival rate as

well as the service time distribution are ignored in

the optimization model as it uses the total number of

calls received in each time period and an estimation

of the average busy fractions. At this point, the

performances obtained from the simulation model

can be said to be more relevant and reliable.

Further comparisons between the best solution

(alternative 1) and the initial scenario were made by

using the distribution of response time in order to

test the robustness of the redeployment solution by

insuring that the responses that occur within larger

target times’ performances are not decreased

compared to the actual performances. The results

depicted in Figure 3 show that up to a target time of

50 minutes, the redeployment plan based on the

alternative 1 solution always provided better

response time performances than those obtained

from the initial model for both priorities 1 and 2.

The larger differences are obtained for a target time

of 15 minutes (15% ± 0,3% for priority 1 and 13,9%

± 0,1% for priority 2).

6 CONCLUSIONS

This research used a multi-period probabilistic

mathematical model for the location of rescue teams

and a discrete event simulation model embed in an

iterative method to help the SAMU-94 managers in

improving the system response time performances.

The optimization model aims to maximize the

demand covered within a target time under limited

resources, while the simulation model is used both to

EmergencyAmbulanceDeploymentinVal-de-MarneDepartment-ASimulation-basedIterativeApproach

573

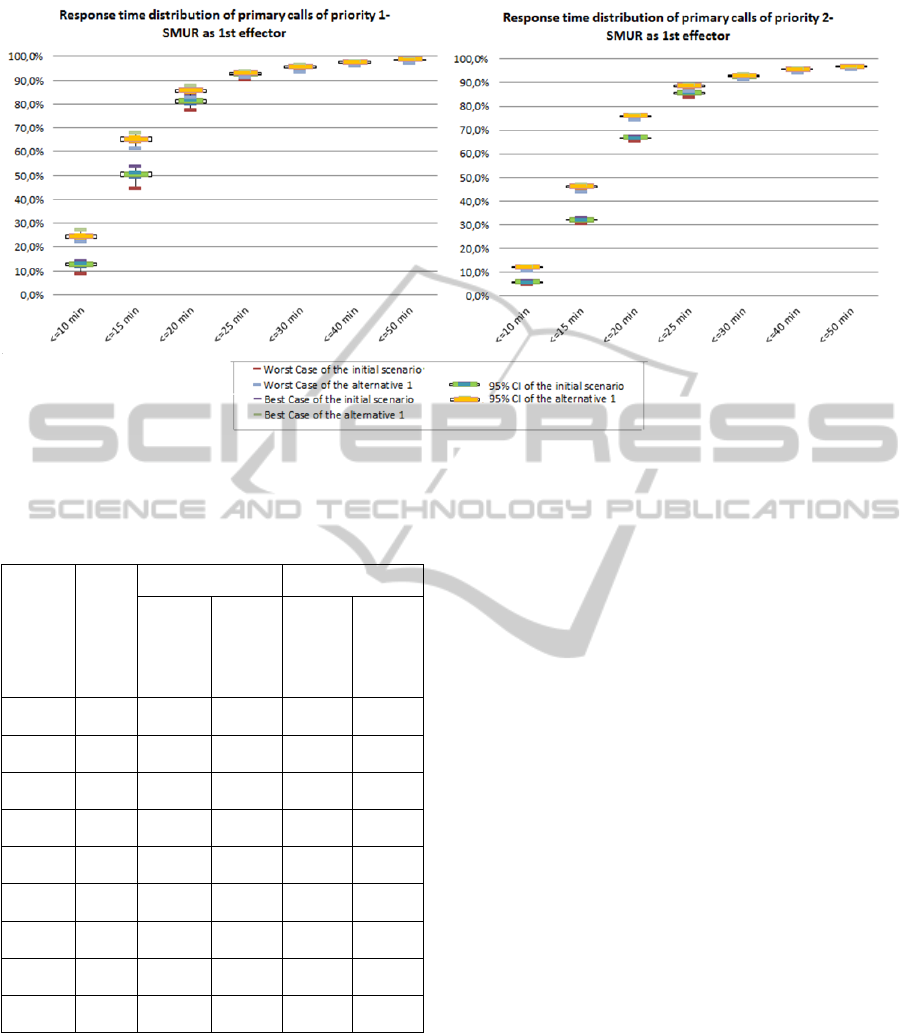
Response time distribution of primary calls of priority 1 –

SMUR as 1st effector

Response time distribution of primary calls of priority 2 –

SMUR as 1st effector

Figure 3: Comparison between the initial scenario and the alternative 1 response time distribution.

Table 2: Comparison of performance measures between

the initial scenario and the converging points for the

different alternatives.

Alternative

Number

iterations

onvergen

Priority 1 Priority 2

Optimal

expected

coverage

within S

Simulat

response

time

within

15 min

Optimal

expecte

coverag

e within

Simulat

response

time

within

20 min

Alt. 1 7 47,4%

65,3% ±

0,9%

88,0%

75,8% ±

0,3%

Alt. 2 6 54,0%

64,7% ±

0,7%

86,3%

75,0% ±

0,3%

Alt. 3 5 60,4%

63,1% ±

0,7%

72,2% ±

0,3%

Alt. 4 6 96,7%

63,4% ±

0,8%

89,0%

75,7%±

0,3%

Alt. 5 6 97,6%

63,7%±

0,6%

89,1%

75,8%±

0,4%

Alt. 6 4 98,2%

63,5% ±

0,8%

98,3%

74,8% ±

0,3%

Alt. 7 7 98,5%

62,3% ±

0,9%

98,5%

74,7% ±

0,4%

Alt. 8 4 99,0%

63,2% ±

0,8%

73,8% ±

0,3%

Initial

scenario

- -

50,3% ±

0,9%

66,6% ±

0,3%

estimate the busy fractions needed as input data in

the analytical model and to obtain reliable estimates

of the system performances given the location

solutions obtained from the optimization model. The

experimental results suggested that the iterative

method could increase the percentage of the demand

covered within 15 minutes up to 29,7% and 43,3%

compared to the current SAMU-94 system for

priority 1 and 2 respectively.

One shortcoming of the proposed redeployment

solution is that it is obtained from the historical

demand data of the SAMU-94. One possible

extension of this work can therefore be based on

forecasting the number of expected emergency calls

so as to derive sufficiently robust relocation strategy

of SMUR teams that covers future demand at the

desired service level. Another area of improvement

for this study is to combine the iterative method

solutions with other scenarios such as increasing the

number of the SAMU-94 resources or implementing

efficient dispatching policies so as to achieve more

considerable improvements in response time

performances.

REFERENCES

Aringhieri, R., Carello, G., Morale, D., 2007. Ambulance

location through optimization and simulation: the case

of Milano urban area, in: 38th Annual Conference of

the Italian Operations Research Society Optimization

and Decision Sciences.

Batta, R., Dolan, J. M., Krishnamurthy, N. N., 1989. The

Maximal Expected Covering Location Problem:

Revisited. Transportation Science 23, 277–287.

Berlin, G. N., Liebman, J. C., 1974. Mathematical analysis

of emergency ambulance location. Socio-Economic

Planning Sciences 8, 323–328.

Bianchi, G., Church, R. L., 1988. A hybrid FLEET model

for emergency medical service system design. Social

science & medicine 26, 163–171.

Church, R., ReVelle, C., 1974. The maximal covering

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

574

location problem. Papers of the Regional Science

Association 32, 101–118.

Cummins, R. O., 1989. From concept to standard-of-care?

Review of the clinical experience with automated

external defibrillators. Annals of Emergency Medicine

18, 1269–1275.

Daskin, M. S., 1983. A Maximum Expected Covering

Location Model: Formulation, Properties and

Heuristic Solution. Transportation Science 17, 48–70.

Daskin, M. S., Stern, E. H., 1981. A Hierarchical

Objective Set Covering Model for Emergency Medical

Service Vehicle Deployment. Transportation Science

15, 137–152.

Eaton, D. J., Héctor, M. L., Sanchez, U., Lantigua, R. R.,

Morgan, J., 1986. Determining Ambulance

Deployment in Santo Domingo, Dominican Republic.

Journal of the Operational Research Society 37, 113–

126.

Fitzsimmons, J. A., 1971. An emergency medical system

simulation model, in: Proceedings of the 1971 Winter

Simulation Conference. ACM, New York, NY, USA,

pp. 18–25.

Fujiwara, O., Makjamroen, T., Gupta, K. K., 1987.

Ambulance deployment analysis: A case study of

Bangkok. European Journal of Operational Research

31, 9–18.

Gendreau, M., Laporte, G., Semet, F., 1997. Solving an

ambulance location model by tabu search. Location

Science 5, 75–88.

Goldberg, J., Dietrich, R., Chen, J. M., Mitwasi, M.,

Valenzuela, T., Criss, E., 1990a. A simulation model

for evaluating a set of emergency vehicle base

locations: Development, validation, and usage. Socio-

Economic Planning Sciences 24, 125–141.

Goldberg, J., Dietrich, R., Ming Chen, J., Mitwasi, M. G.,

Valenzuela, T., Criss, E., 1990b. Validating and

applying a model for locating emergency medical

vehicles in Tuczon, AZ. European Journal of

Operational Research 49, 308–324.

Gunes, E., Szechtman, R., 2005. A simulation model of a

helicopter ambulance service, in: Proceedings of the

2005 Winter Simulation Conference.

Harewood, S. I., 2002. Emergency ambulance deployment

in Barbados: a multi-objective approach. Journal of the

Operational Research Society 53, 185–192.

Henderson, S. G., Mason, A. J., 2005. Ambulance Service

Planning: Simulation and Data Visualisation, in:

Brandeau, M.L., Sainfort, F., Pierskalla, W.P. (Eds.),

Operations Research and Health Care. Kluwer

Academic Publishers, Boston, pp. 77–102.

Hogan, K., ReVelle, C., 1986. Concepts and Applications

of Backup Coverage. Management Science 32, 1434–

1444.

Inakawa, K., Furuta, T., Suzuki, A., 2010. Effect of

Ambulance Station Locations and Number of

Ambulances to the Quality of the Emergency Service,

in: The 9th International Symposium on Operations

Research and Its Applications (ISORA’10). Chengdu-

Jiuzhaigou, China, pp. 340–347.

Ingolfsson, A., Erkut, E., Budge, S., 2003. Simulation of

single start station for Edmonton EMS. The Journal of

the Operational Research Society 54, 736–746.

Kelton, W. D., Sadowski, R. P., Sturrock, D. T., 2008.

Simulation with Arena, 4th edition. ed. McGraw-Hill,

New York, NY, USA.

Koch, O., Weigl, H., 2003. Modeling ambulance service

of the Austrian Red Cross, in: Proceedings of the 2003

Winter Simulation Conference. S. Chick, P. J.

Sánchez, D. Ferrin, and D. J. Morrice, eds, pp. 1701 –

1706.

Larson, R. C., 1974. A hypercube queuing model for

facility location and redistricting in urban emergency

services. Computers & Operations Research 1, 67–95.

Lee, T., Cho, S.-H., Jang, H., Turner, J. G., 2012. A

simulation-based iterative method for a trauma center:

air ambulance location problem, in: Proceedings of the

2012 Winter Simulation Conference. . C. Laroque, J.

Himmelspach, R. Pasupathy, O. Rose, and A.M.

Uhrmacher.

Liu, M. S., Lee, J. T., 1988. A Simulation Of A Hospital

Emergency Call System Using SLAMII. Simulation

51, 216–221.

Lubicz, M., Mielczarek, B., 1987. Simulation modelling of

emergency medical services. European Journal of

Operational Research 29, 178–185.

Marianov, V., Revelle, C., 1994. The queuing probabilistic

location set covering problem and some extensions.

Socio-Economic Planning Sciences 28, 167–178.

Peleg, K., Pliskin, J. S., 2004. A geographic information

system simulation model of EMS: reducing ambulance

response time. The American Journal of Emergency

Medicine 22, 164–170.

Repede, J. F., Bernardo, J. J., 1994. Developing and

validating a decision support system for locating

emergency medical vehicles in Louisville, Kentucky.

European Journal of Operational Research 75, 567–

581.

ReVelle, C., Hogan, K., 1989. The Maximum Availability

Location Problem. Transportation Science 23, 192–

200.

ReVelle, C. S., Marianov, V., 1991. A probabilistic

FLEET model with individual reliability requirements.

European Journal of Operational Research 53, 93–105.

Savas, E. S., 1969. Simulation and Cost-Effectiveness

Analysis of New York’s Emergency Ambulance

Service. Management Science 15, 608–627.

Silva, P. M. S., Pinto, L. R., 2010. Emergency medical

systems analysis by simulation and optimization, in:

Proceedings of the 2010 Winter Simulation

Conference. B. Johansson, S. Jain, J. Montoya-Torres,

J. Hugan, and E. Yücesan, eds, pp. 2422 –2432.

Su, S., Shih, C. L., 2003. Modeling an emergency medical

services system using computer simulation. Int J Med

Inform 72, 57–72.

Toregas, C., Swain, R., ReVelle, C., Bergman, L., 1971.

The Location of Emergency Service Facilities.

Operations Research 19, 1363–1373.

Uyeno, D. H., Seeberg, C., 1984. A practical methodology

for ambulance location. Simulation 43, 79–87.

EmergencyAmbulanceDeploymentinVal-de-MarneDepartment-ASimulation-basedIterativeApproach

575

Van Buuren, M., van der Mei, R., Aardal, K., Post, H.,

2012. Evaluating dynamic dispatch strategies for

emergency medical services: TIFAR simulation tool,

in: Proceedings of the 2012 Winter Simulation

Conference. C. Laroque, J. Himmelspach, R.

Pasupathy, O. Rose, and A.M. Uhrmacher, pp. 46:1–

46:11.

Vukmir, R. B., 2006. Survival from prehospital cardiac

arrest is critically dependent upon response time.

Resuscitation 69, 229–234.

Wang, Y., Luangkesorn, K. L., Shuman, L., 2012.

Modeling emergency medical response to a mass

casualty incident using agent based simulation. Socio-

Economic Planning Sciences 46, 281–290.

Wears, R. L., Winton, C. N., 1993. Simulation modeling

of prehospital trauma care, in: Proceedings of the 1993

Winter Simulation Conference. G.W. Evans, M.

Mollaghasemi, E.C. Russel, W.E. Biles.

White, R., Asplin, B., Bugliosi, T., Hankins, D., 1996.

High Discharge Survival Rate After Out-of-Hospital

Ventricular Fibrillation With Rapid Defibrillation by

Police and Paramedics. Annals of Emergency

Medicine 28, 480–485.

SIMULTECH2013-3rdInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

576