Role of Human Perception in Cluster-based Visual Analysis of

Multidimensional Data Projections

Ronak Etemadpour

, Robson Carlos da Motta

, Jose Gustavo de Souza Paiva

, Rosane Minghim

Maria Cristina Ferreira de Oliveira

and Lars Linsen

Jacobs University Bremen, Bremen, Germany

Universidade de S

ao Paulo, S

ao Carlos, Brazil

Federal University of Uberl

andia, Uberl

andia, Brazil

Keywords:

Projections, Multidimensional Data, Perception-based Evaluation.

Abstract:

Visualization of high-dimensional data requires a mapping to a visual space. Whenever the goal is to preserve

similarity relations, multidimensional projections or other dimension reduction techniques are commonly used

to project high-dimensional data point to a 2D point using a certain strategy for the 2D layout.Typical analysis

tasks for projected multidimensional data do not necessarily match the expectations of human perception.

Learning more about the effectiveness of projection layouts from a users perspective is an important step

towards consolidating their role in supporting visual analytics tasks. Those tasks often involve detecting and

correlating clusters. To understand the role of orientation and cluster properties of size, shape and density, we

ﬁrst conducted a study with synthetic 2D scatter plots, where we can set the respective properties manually.

Then we picked ﬁve projection methods representative of different approaches to generate layouts of high

dimensional data for two domains, image and document data. The users were asked to identify the clusters

on real-world data and answers to questions were compared for correctness against ground truth computed

directly from the data. Our results offer interesting insight on the use of projection layouts in data visualization

tasks.

1 INTRODUCTION

Multidimensional data analysis aims to verify the ex-

istence of patterns and trends in sets of instances,

by the detection of the overall data distribution, and

by the observation of clusters or correlations. This

analysis can be visually performed by the use of

information visualization techniques. Multidimen-

sional projections are examples of these techniques,

in which the original dimensions are projected to a

lower-dimensional space (typically 2D), and the in-

stances are then displayed as 2D scatter plots. This

mapping process inevitably leads to information loss,

and different strategies can be applied to develop pro-

jection methods that preserve certain properties of the

data distribution. Often a compromise between dif-

ferent design goals is necessary. In this sense, the

quality of the projected views can be analyzed by esti-

mating how well certain design goals were met. Such

quality measures are typically based on distances be-

tween points in the multidimensional space and the

projected space. What is often neglected however is

the fact that the projected views are interpreted by hu-

mans, and that a natural mathematical formalization

may not sufﬁce to guarantee that the automatic evalu-

ations of clusterings will seem natural to the users.

The goal of this paper is to investigate the role

of human perception when analyzing projected views.

Our hypothesis is that cluster properties affect the hu-

man interpretation. For example, we assume that dis-

tance may be perceived incorrectly because of percep-

tional cues being triggered. In particular, we focus on

the role of cluster density, shape, size, and orientation

when performing typical visual analysis tasks.

To investigate the perceptual factor, we formulated

hypotheses, see Section 3, and conducted a user study

to test against them. Subjects were asked to per-

form typical visual analysis tasks on project views,

which have been obtained by applying a representa-

tive selection of projection methods to multidimen-

sional data sets from two domain. For several aspects,

it was important to only modify one cluster property,

while keeping the others unchanged. Since this is ba-

sically impossible to achieve with real data projec-

tions, we had to rely on some synthetically generated

scatterplots, see Section 4. We performed a statistical

analysis of the outcome of the user study. Section 5

presents our ﬁndings and conclusions.

276

Etemadpour R., Carlos da Motta R., de Souza Paiva J., Minghim R., Ferreira de Oliveira M. and Linsen L..

Role of Human Perception in Cluster-based Visual Analysis of Multidimensional Data Projections.

DOI: 10.5220/0004682102760283

In Proceedings of the 5th International Conference on Information Visualization Theory and Applications (IVAPP-2014), pages 276-283

ISBN: 978-989-758-005-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 RELATED WORK

Multidimensional projection techniques can be di-

vided into two major groups namely linear and non-

linear projection techniques. Linear projection tech-

niques create linear combinations of the data at-

tributes, deﬁning them in a new orthogonal basis of

lower dimensionality. Among such techniques, PCA

(Principal Component Analysis) (Jolliffe, 1986) is of-

ten employed to generate similarity layouts by reduc-

ing data to two or three dimensions. Nonlinear tech-

niques attempt to minimize a function of the informa-

tion loss incurred by the projection. Normally, this

function is based on the dissimilarities among the in-

stances or on distances among the multidimensional

points. Non-linear projection techniques can be estab-

lished using Multidimensional Scaling (MDS) (Borg

and Groenen, 2010) that aims at maintaining dis-

tances within a cluster. Isomap is a method that ex-

tends the metric of multidimensional scaling (MDS)

by incorporating the geodesic distances imposed by

a weighted graph and tries to maintain distances be-

tween clusters according to that metric (Tenembaum

et al., 2000). Here and within our paper, a cluster

refers to a subset of the multidimensional data points

that are similar to each other and dissimilar to points

not belonging to the subset. Force-directed place-

ment approaches are a class of algorithms for draw-

ing graphs. Their purpose is to position the nodes of

a graph such that all the edges are connected with a

virtual spring of length proportional to the distance

between the corresponding data points. A spatial em-

bedding is obtained with an iterative simulation of the

spring forces acting on this hypothetical physical sys-

tem by assigning forces to the set of edges and nodes

based on their relative positions and using these forces

to simulate the motion of the edges and nodes or to

minimize their energy.

Many numerical measures have been introduced

to estimate the quality of layouts produced by pro-

jection methods. Estimates such as the silhouette co-

efﬁcient (Tan et al., 2005) combine concepts of both

cohesion and separation for both individual points and

clusters. For an individual point i, it calculates a factor

a as an average distance of i to the points in its clus-

ter and a factor b as the minimum average distance of

i to points in another cluster. The silhouette coefﬁ-

cient for a point is then given by S = 1 −

if a < b or

S =

− 1 if a ≥ b. The value lies between 0 and 1,

where higher values imply performance. Neighbor-

hood hit (Paulovich et al., 2008) evaluates the projec-

tions capability of preserving the neighborhood rela-

tionships among the points. Several approaches for

selecting good layouts have been proposed, including

visual approaches that plot quality measures in graph-

ical form. The correlation coefﬁcient (Geng et al.,

2005) between the distance vectors, that contain the

distances between all pairs of points, provide a mea-

surement of the validity by evaluating distances. Be-

trini et al. (Bertini et al., 2011) started a collection of

quality metrics in high-dimensional data visualization

that have been used in a variety of contexts and pur-

poses and provided a way to reason about their char-

acteristic features. Authors presented an analysis of

the visualization techniques, the quality metrics, and

the processing pipeline. They derived a set of factors

for discriminating the quality metrics, visualization

techniques, and the process. However, the perceptual

factor in interpreting the projected views has majorly

been neglected in all these numerical measures.

Rensink and Baldridge (Rensink and Baldridge,

2010a; Rensink and Baldridge, 2010b) presented a

rigorous way to evaluate the visual perception of

correlation in scatter plots based on classical psy-

chophysical methods originally developed for simple

properties such as brightness. The scatter plots were

considered containing 100 points with a bivariate nor-

mal distribution. Means were 0.5 of the range of

the points, and standard deviations 0.2 of this range.

Precision as well as accuracy over all correlations of

the scatter plots have been described by two related

functions governed by two parameters. Accuracy was

measured using reference scatter plots with ﬁxed up-

per and lower values, with a test scatter plot adjusted

so that its correlation appeared to be halfway between

these. Results of the discrimination tests has shown

that just noticeable differences in correlation can be

described by a variability parameter and an offset pa-

rameter. Authors believe that precision is proportional

to offset and accuracy is proportional to the logarithm

of this quantity. Their approach did not consider vi-

sual analysis task though.

Tatu et al. (Tatu et al., 2010) investigated quality

measures computed from projections from a user per-

ception perspective. In their user study, subjects were

confronted with a set of 18 scatter plots and asked

to select and rank the ﬁve most useful ones for the

task of best separating three given classes encoded by

color, considering a single data set. They did not look

into arbitrary multidimensional data projections. Al-

buquerque et al. (Albuquerque et al., 2011) attempted

to ﬁnd a perception-based quality measure for scat-

ter plots, constructing a perceptual embedding for the

different projections based on the data from a psy-

chophysics study and multidimensional scaling. This

embedding together with a ranking function was then

used to estimate the value of the projections for a

speciﬁc user task in a perceptual sense. This rank-

RoleofHumanPerceptioninCluster-basedVisualAnalysisofMultidimensionalDataProjections

277

ing evaluates scatter plots for ﬁnding correlation be-

tween the dimensions and separation between classes.

Sedlmair et al. (Sedlmair et al., 2012) proposed a tax-

onomy of visual cluster separation factors in scatter

plots and presented an in-depth qualitative evalua-

tion of two recently proposed and validated separa-

tion measures. They found that quality assessment of

cluster separation by these measures was highly dis-

crepant with human assessments obtained from sys-

tematic inspection by two researchers with the mea-

sures showing a high number of failure cases. In their

qualitative data study, two investigators visually in-

spected over 800 plots to determine whether or not

the measures created plausible results. Their cate-

gories is split into within-cluster and between-cluster

factors and ordered by their ability to inﬂuence scale,

point distance, shape, and position. This work is

most closely related to ours, as we are considering the

role of cluster properties when interpreting projected

views. We enhance their ﬁndings by evaluating the

factors that inﬂuence the perception.

Concerning the role of rotation of scatter plots and

shape of clusters in 2D layouts, it is worth mention-

ing the work by Healey et al. (Healey et al., 1996)

on pre-attentive features with respect to orientation

as well as the Gestalt laws presented by Ware (Ware,

2000), respectively. Healey et al. believe that stud-

ies from pre-attentive vision can assist in the design

of visualization tools. They have tested visual fea-

tures that can be detected in this way, orientation and

hue, that caused rapid and accurate numerical estima-

tion. Furthermore, random variation in one of these

features resulted in no interference when subjects es-

timated the percentage of the other. There has also

been some fundamental work on the Gestalt princi-

ples within the cognitive psychology community that

relate to our work. The Gestalt principles describe

psychological phenomena underlying human percep-

tion of given tasks by viewing them as organized and

structured wholes. For the detection of non-spherical

clusters, various researchers sought more robust ways

to identify arbitrarily shaped clusters rather than the

sum of their constituent parts computationally.

Ahuja et al. (Ahuja and Tuceryan, 1998) studied

a computational approach presented to extract basic

perceptual structure or the lowest level grouping in

dot patterns aiming at extracting the perceptual seg-

ments of dots due to their relative locations. The

grouping was seeded by assigning to dots their lo-

cally evident perceptual roles and iteratively modi-

fying the initial estimates to enforce global Gestalt

constraints. The result was a partitioning of the dot

pattern into different perceptual segments or tokens

and the grouping was accomplished by interpreting

dots as belonging to interior or border of a perceptual

segment, being along a perceived curve, or being iso-

lated. At the lowest perceptual level the segments of

dots grouped together, because of their relative loca-

tions. Mayorga and Gleicher (Mayorga and Gleicher,

2013) provided a new technique for displaying point

data that scales well with the number of points. They

believed that scatter plots suffer from overdraw as the

number of points per unit area increases. Based on

the Gestalt law of proximity (Ware, 2000), that per-

ception tends to group similar objects that are close

together as part of a greater whole, visual estimates of

density within the group in a 2D display may be im-

possible. Since the shape of the perceived grouping

may not match the distribution of density in the un-

derlying data, they used contours to aggregate points.

3 HYPOTHESES

In our study, we want to investigate whether only the

distances (in projected space) matter or whether other

cluster properties inﬂuence subjects decisions on typ-

ical visual analysis tasks. We assume that the density

of points within clusters and the size of clusters can

impact the interpretation of distances and grouping.

According to Gestalt laws, the shape and orientation

of a cluster should also inﬂuence decisions during vi-

sual analysis. For example, when two stretched clus-

ters are aligned, they may be perceived as a continu-

ation of one cluster. Or, features may be more easily

perceived when they align with a horizontal or vertical

axis. Following these ideas, we formulate the follow-

ing hypotheses for cluster-based visual analysis tasks:

H1) Cluster density (in projected space) inﬂuence the

answers to the tasks, H2) Cluster size (in projected

space) inﬂuence the answers to the tasks, H3) Clus-

ter shape (in projected space) inﬂuence the answers to

the tasks, and H4) Rotation affects the performance of

projections.

4 DESIGN OF USER STUDY

In the following, we describe the design of our user

study. We ﬁrst describe the tasks that we considered

for multidimensional data analysis using scatter plots

in a projected 2D visual space. Then, we describe the

data sets and projections employed in our user study,

followed by a description of the synthetic examples

we generated. Finally, we describe the experimental

set-up of the user study and how the outcome was an-

alyzed.

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

278

4.1 Tasks

We identify typical analysis tasks for multidimen-

sional data. Such tasks are often concerned with iden-

tifying clusters and investigating distances (or simi-

larities) within clusters or between clusters or yet be-

tween an individual point and clusters.

A relation-seeking task is to investigate the simi-

larities between subgroups. The subgroups represent

clusters or individual objects. Hence, we are inter-

ested in investigating whether a point (or object) is

more similar to one cluster or to another. Similarly,

we are interested in investigating whether a cluster is

more similar to a second cluster or a third. Conse-

quently, we deﬁned the two tasks:

Q1: Identify the closest cluster to a given object.

Q2: Identify the closest cluster to a given cluster.

In both tasks, we consider two clusters (color-

coded by green and blue) and try to determine

whether the green or the blue cluster is closer to the

reference (depicted in red). The colors blue and green

are assigned randomly to the clusters to avoid any bias

towards a speciﬁc color.

A pattern-identiﬁcation task is to detect clusters

within a given point distribution. For a given scatter

plot, we asked the subjects to identify and report back

the number of clusters, deﬁning the task:

Q3: Estimate the number of clusters in a given

point distribution (scatterplot).

Here, all points are colored in blue.

4.2 Projections

We selected four techniques as representatives of

three distinct strategies for embedding data in two

dimensions, namely statistical dimension reduction,

MDS, and force-directed placement. We also in-

cluded a technique based on similarity trees (Cuadros

et al., 2007), which is a different type of point place-

ment and had not been previously used as a projec-

tion. The techniques picked are PCA (Principal Com-

ponent Analysis) (Jolliffe, 1986), Isomap (Isometric

Feature Mapping) (Tenembaum et al., 2000), LSP

(Least Square Projection) (Paulovich et al., 2008),

Glimmer (Ingram et al., 2009), and NJ tree (Paiva

et al., 2011) layout. Our choice covers modern and

classic techniques that have been introduced aiming

at capturing different data behaviors.

PCA is a classical dimension reduction strategy,

often employed to generate visual embeddings of

data, which uses an orthogonal transformation to con-

vert a set of observations of possibly correlated vari-

ables into a set of values of linearly uncorrelated vari-

ables. 2D layouts are obtained considering the two

ﬁrst principal components, at the risk of disregarding

other potentially relevant components.

LSP is a multidimensional projection technique

based on least square approximations that compute

the coordinates of a set of projected points based on

the coordinates of a reduced number of control points

with deﬁned geometry. From an initial projection of

the control points, it builds a linear system from infor-

mation given by the projected points and their neigh-

borhoods, which is solved to obtain a 2D embedding

of the remaining data points. A Laplacian operator

ensures that points in a particular neighborhood re-

main proximate in the target space. The choice of rep-

resentatives affects precision of the resulting layout,

with good results achieved with sampling by cluster-

ing. LSP is a fast and modern technique that is also

accurate according to high quality measurements.

Isomap is one of the most promising nonlinear di-

mension reduction techniques that replaces the orig-

inal distances by geodesic distances computed on a

graph to obtain a globally optimal solution to the

distance preservation problem. A weighted nearest

neighbor graph is built from the data, with pairwise

point distances as edge weights. The shortest path

in this graph gives the distance between two points.

Isomap is effective on data that present non-linear re-

lationships, that both PCA and classical scaling typi-

cally fail to detect. However, when Isomap is applied

to real-world data, it shows some limitations, such as

being sensitive to noise.

Glimmer is a recent technique representative of

force-directed placement MDS and used for perform-

ing metric distance scaling. It uses the GPU to reduce

the total computation time and it employs a hierarchi-

cal approach to improve the quality of the ﬁnal solu-

tion. In Glimmer the iterative point placement proce-

dure is highly optimized by usage of GPU hardware

combined with a multilevel strategy that operates on

a hierarchical model of the underlying particle-spring

system. It is also fast and generates good quality lay-

outs as evaluated by stress preservation measures.

NJ tree is a faster alternative to the original NJ-tree

layout algorithm (Cuadros et al., 2007) and generates

more precise layouts. Tree layouts favor good perfor-

mance on tasks that require visual segregation of clus-

ters. We wanted to check whether their good grouping

and distance properties would be perceived by users

in the same way as the projections if the edges are re-

moved from the layouts. The internal nodes as well as

the lines depicting the branches were removed from

the layouts to obtain scatterplots of the data points,

similar to the other layouts shown to subjects. We re-

fer to these as Tree projection layouts, or just NJ.

RoleofHumanPerceptioninCluster-basedVisualAnalysisofMultidimensionalDataProjections

279

4.3 Multidimensional Data Sets

We identiﬁed two multidimensional data domains ex-

hibiting different characteristics. The ﬁrst application

is the visual analysis of document collections. Each

document represents a data object. The corresponding

multidimensional point is a feature vector that repre-

sents the frequency of occurrences of representative

words (keywords) in the document. The second ap-

plication is the visual analysis of image collections.

Each image represents an object and the correspond-

ing multidimensional point is a vector of features that

are derived from the image using image processing

steps. Document data are typically of very high di-

mensionality when compared to the number of ob-

jects, which imposes a certain data sparseness. Im-

age feature vectors are typically of signiﬁcantly lower

dimensionality, which leads to a generally denser dis-

tribution.

We use two document and two image data sets.

The ﬁrst document data set - referred to as CBR - con-

tains 680 objects with 1,423 dimensions. The docu-

ment information includes title, authors, abstract, and

references from scientiﬁc papers in four different sub-

jects

. The second document data set - referred to as

KDViz - contains 1,624 objects with 520 dimensions

and four highly unbalanced labels generated from an

Internet repository

. The ﬁrst image data set - re-

ferred to as Corel

- contains 1,000 objects with 150

dimensions. The images are photographs on ten dif-

ferent themes (Li and Wang, 2003). The second im-

age data set - referred to as Medical - contains 540 ob-

jects with 28 dimensions (features) including Fourier

descriptors and energies derived from histograms as

well as mean intensity and standard deviation com-

puted from the images themselves. Table 1 shows the

projected layouts of all four data sets obtained with

each of the ﬁve projections identiﬁed in this section.

Colors reﬂect the data class labels provided by the ap-

plication.

4.4 Synthetic Data

One of the modern psychological rules that was ap-

plied to visual and pattern perception is called Gestalt

approaches (Wertheimer, 2005). Our goal is to exam-

ine whether it is just (Euclidean) distances that matter

when visually analyzing the scatter plots or whether

there are other characteristics of the clusters that inﬂu-

ence the visual analysis from a perceptual view. The

characteristics we investigated were cluster density

http://vicg.icmc.usp.br/infovis2/DataSets

UCI KDD Archive, http://kdd.ics.uci.edu

Table 1: The layouts obtained with the ﬁve tested projec-

tions on the four data sets investigated. Circle color indi-

cates instance class label.

Glimmer Isomap LSP PCA Tree

CBR

KDViz

Corel

Medical

(i.e., point density within a cluster as deﬁned above),

cluster size (i.e., the number of objects or points that

belong to a cluster), and cluster shape (e.g., whether

a cluster appears to be round or elongated). When ex-

amining the role of cluster density, cluster size, and

cluster shape on Tasks Q1 and Q2, we need examples

where only one of these parameters varies while the

others remain constant.

We ﬁrst generated 2D scatter plots where the two

examined clusters have the same (or similar) shape

and size, while the density varies. We picked a round

shape as default and points are placed uniform ran-

domly within the given area of the cluster. Then, we

generated scatter plots, where the size (i.e., number

of points) was changing and we looked into chang-

ing size and density simultaneously (shape remained

roundish).

Next, we generated scatter plots with varying

shapes, i.e., one cluster was more roundish and an-

other one more longish, while density and size were

the same. A scatter plot has also been created with

two longish clusters, one bent and the other straight.

The bending may be in the direction away or towards

the reference point. The examples are shown in Fig-

ure 1. We also added a control scatter plot, where both

clusters have the same density, size, and shape.

4.5 Experimental Set-up

For each of the ﬁve projection techniques and each of

the four data sets, we generated a scatter plot visual-

ization of the projected layout, leading to 20 scatter

plots. Let us ﬁrst consider the investigation of the ori-

entation. In (Healey et al., 1996) two unique orienta-

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

280

(a) (b) (c)

Figure 1: Task Q1: Finding closest cluster to reference point

for synthetic data with varying cluster shape. (a) one cluster

is more bent and the other more longish; (b) the reference

point is located in a direction orthogonal; (c) the reference

point is located in a space between two clusters.

tions were used, 0

◦

rotation and 60

◦

rotation. Here, we

picked the cluster-identifying task (Task Q3) and ran-

domly generated rotated views of 45

◦

and 60

◦

in math-

ematically positive or negative direction for all ﬁve

projections and all four data sets.

In addition, we manually generated 2D scatter

plots using the synthetic clusters described above that

vary in density, size, and shape. The manually gener-

ated scatter plots consist of the two clusters encoded

by color and another cluster (Task Q2) or an object

(Task Q1), respectively, located between them at an

equal distance from both (deﬁned as the minimal dis-

tance between the clusters objects). Hence, if only

distances matter, we expect that subjects in about 50%

of the cases choose the ﬁrst cluster and in about 50%

of the cases choose the second cluster for the distance-

based Tasks Q1 and Q2. We created 20 synthetic im-

ages as the examples shown in Table 2. This leads to

a total of 40 scatter plots for all conducted studies.

Given the high number of scatter plots, the body

of subjects was divided into two groups. The ﬁrst

group of 31 students was assigned the Tasks Q1 and

Q2 for the synthetic data, while the second group of

30 students was assigned the Tasks Q3 for the pro-

jected multidimensional data. Subjects assigned the

same task set executed them in the same (random) se-

quence and saw the same images. All subjects ful-

ﬁlled their tasks in two sessions with a short break

in between. The body of subjects consisted of 61

students at an undergraduate or graduate level in the

ﬁelds of applied mathematics and computer science.

They had not been engaged with projections in depth,

although they possibly had different levels of knowl-

edge about projections. They were provided with a

20-minutes introduction on projections, scatter plots,

and the setup of the user study. It was not necessary

to confront them with the applications behind the data

(document and image data).

The system always ﬁrst presented the task to the

subjects. Once they felt comfortable about having

understood the task, they were confronted with a se-

quence of still images showing the respective scatter

plots. For each image they were asked to answer the

question as soon as they knew the answer. To force

participants to act as quickly as possible, we intro-

duced a time limit. In a pilot study with eight par-

ticipants we observed that it took them on average

7.7 seconds to fulﬁll the tasks and the average max-

imum time was 24.75 seconds. Therefore, in the ac-

tual study we gave the participants 30 seconds to com-

plete the tasks, after which the scatter plot image dis-

appeared. The question would remain until answered.

4.6 Statistical Analysis

For the projected multidimensional data, we com-

puted means and standard deviation of the errors.

Given the ground truth for the real data, we can com-

pute the errors in the answers of the subjects for Task

Q3 that required the subjects to estimate a number as

follows:

e =

true

− n

answer

true

· 100,

where n

true

is the estimated ground truth and n

answer

is the reported answer.

To test for statistical signiﬁcance of the individ-

ual results, we ﬁrst tested the distribution of the error

values against normality using the Shapiro-Wilk tests.

In case of non-normal distribution, we applied the

Wilcoxon test on non-parametric two related samples

when comparing two groups. In case of normal dis-

tribution, we used t-test when comparing two groups.

For the investigations with statistical methods on

synthetic data, the set-up was such that it was ex-

pected that approximately 50% of the subjects would

give one of the two possible answers. It was tested

whether the results deviate signiﬁcantly from the ex-

pected value using a two-tailed binomial test.

5 RESULTS

When looking at Tasks Q1 and Q2 for the synthetic

examples, one would expect that roughly half of the

subjects would pick one cluster as the closer one and

half the other one, as the distances of the highlighted

cluster (Task Q2) or object (Task Q1) to the given two

clusters are the same. Indeed, for our control exam-

ples, where the two given clusters have same density,

size, and shape, the answers follow this expectation.

However, when varying the cluster properties, an-

swers showed signiﬁcant biases. When choosing two

clusters with different densities (same size and same

shape), the vast majority of the subjects answered that

the highlighted cluster (87.1%, p < 0.0001) or object

(93.6%, p < 0.0001) is closer to the less dense cluster.

RoleofHumanPerceptioninCluster-basedVisualAnalysisofMultidimensionalDataProjections

281

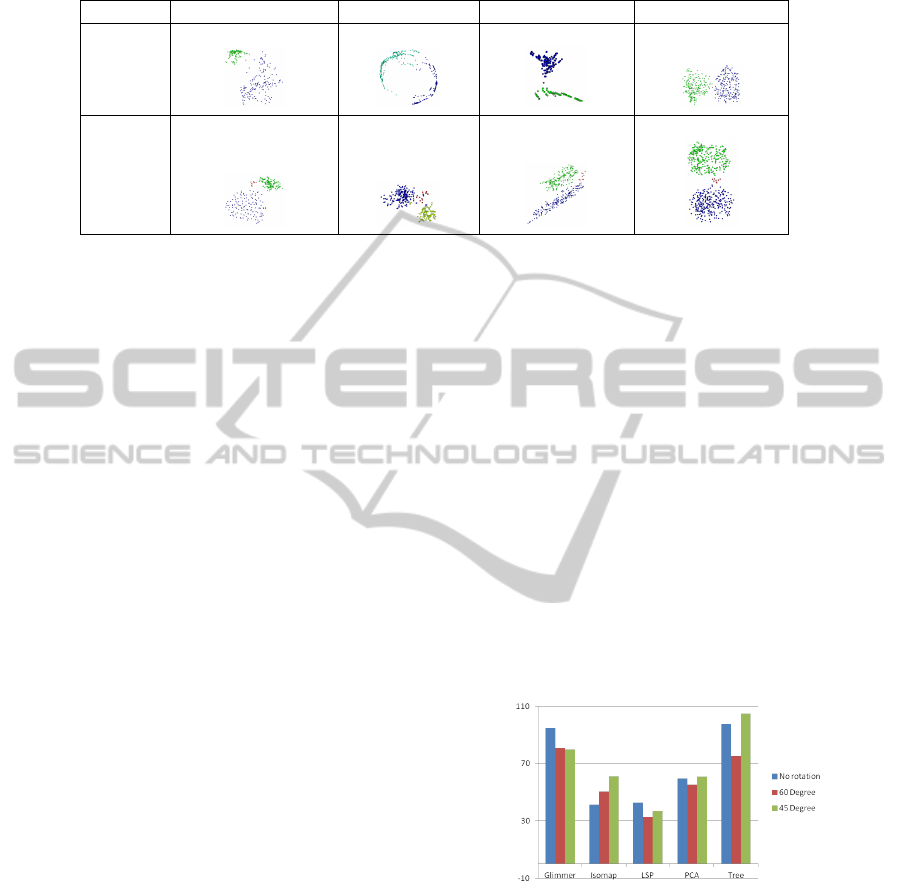
Table 2: Examples for scatter plots used for Tasks Q1 and Q2. The red color indicates the reference object or group, respec-

tively. Green and blue colors encode the two clusters equally distant to the reference.

Changing Density Changing Size Changing Shape Same Properties

Task Q1

Task Q2

When choosing two clusters with different size (same

density and same shape), there was a slight prefer-

ence towards saying that the larger cluster is closer to

the highlighted cluster (54.8%, p = 0.3601) or object

(51.6%, p = 0.5). However, this preference is not sta-

tistically signiﬁcant. We also investigated examples

where both density and size were changed. The ﬁnd-

ings conﬁrm that density is the more dominant cluster

characteristic for the given tasks.

When choosing two clusters with different shape

(same density and same size), we investigated two set-

ups. In a ﬁrst set-up, the highlighted cluster or ob-

ject is located in the principal direction of a longish

given cluster. Surprisingly, this did not lead to a sta-

tistically signiﬁcant increase in choosing this longish

cluster as the one closest to a highlighted object (Task

Q1; 45.2%, p = 0.36) or a highlighted cluster (Task

Q2; 54.8%, p = 0.3601). Hence, the continuation of

the principal direction as a perception of Gestalt did

not play a signiﬁcant role for the given tasks. In a

second set-up, one given cluster was roundish and the

other longish, but the highlighted cluster or object was

not located in the principal direction of the longish

cluster. It was observed that the longish cluster was

considered closer (with statistical signiﬁcance, p =

0.022) in Task Q1 (74.2%), but there was no statis-

tical signiﬁcance for Task Q2 (54.8%, p = 0.3601).

These ﬁndings can provide a starting point for further

investigations on the role of cluster shapes for per-

ceiving distances in scatterplots, e.g., by considering

other shapes and set-ups.

From our experiments, we can conclude that the clus-

ter characteristics do inﬂuence the results, although

not all of them. Density seems to be most important

in this regard. We can conﬁrm Hypotheses H1 and

H3 on density and shape, but not Hypothesis H2 on

size. Figure 2 summarizes the results of the compar-

ative analysis of the ﬁve projections for Task Q3 on

counting the number of clusters. The bar charts show

the mean error values, which are computed accord-

ing to the description in Section 4.6. We analyzed for

each data set, each rotation, and each projection in-

dividually, whether there is a signiﬁcant difference in

the answers obtained when using the original layout

and when using a rotated version. In the vast majority

of the cases, no statistically signiﬁcant difference was

reported. A signiﬁcant difference was observed only

in two exceptional cases, but these exceptions did

not exhibit any noticeable pattern: Wilcoxon Signed

Ranks Test showed signiﬁcant higher error (p= 0.023)

for the 45

◦

rotated view in KDViz dataset compared to

the original scatter plot when using the Tree layout,

and there was also a signiﬁcantly less mean error (p=

0.012) for the 60

◦

rotated view in Corel dataset when

using LSP. In general, there was always a positive cor-

relation (Paired Samples Correlations) for this study,

i.e., people who did well on the rotated one also did

well on the unrotated. Thus, we must reject Hypothe-

sis H4.

Figure 2: Mean error values for Task Q3 on estimate the

number of clusters with different projection methods. Orig-

inal scatterplots (blue) are compared against rotated views

(red and green).

6 CONCLUSIONS

We conducted a controlled user study to evaluate how

users perceive multidimensional data projection lay-

outs when performing typical visual analysis tasks.

In particular, we evaluated the role of cluster charac-

teristics such as density, size, shape, and orientation.

We considered layouts obtained with ﬁve projection

IVAPP2014-InternationalConferenceonInformationVisualizationTheoryandApplications

282

methods on data sets with distinct characteristics in

terms of sparseness and distance distribution. When

there was the need to isolate one of the cluster charac-

teristics, we used synthetic 2D scatter plot examples.

Our ﬁndings were that density and shape of clus-

ters signiﬁcantly affect the perception during a visual

inspection leading to biased instead of balanced re-

sults in our experiments. Cluster size did not lead to

signiﬁcant affects. The orientation of the scatter plots

did also not affect the interpretation signiﬁcantly. In

general, though, we have observed that cluster prop-

erties do inﬂuence the outcome. Hence, perception is

an important aspect when analyzing projections that is

not captured in the typically applied numerical quality

estimates.

ACKNOWLEDGEMENTS

This work was supported by the research center on

Visual Communication and Expertise (VisComX) at

Jacobs University, Bremen, Germany.

REFERENCES

Ahuja, N. and Tuceryan, M. (1998). Extraction of early

perceptual structure in dot patterns: Integrating re-

gion, boundary, and component gestalt. Computer

Vision, Graphics, and Image Processing archive, 48

Issue:3:304–356.

Albuquerque, G., Eisemann, M., and Magnor, M. (2011).

Perception-based visual quality measures. In Proc.

IEEE Symposium on Visual Analytics Science and

Technology (VAST), pages 13–20.

Bertini, E., Tatu, A., and Keim, D. (2011). Quality metrics

in high-dimensional data visualization: An overview

and systematization. IEEE Transactions on Visualiza-

tion and Computer Graphics, 17(12):2203 –2212.

Borg, I. and Groenen, P. J. F. (2010). Modern Multidimen-

sional Scaling Theory and Applications. Springer Se-

ries in Statistics. Springer, 2nd. edition edition.

Cuadros, A. M., Paulovich, F. V., Minghim, R., and Telles,

G. P. (2007). Point placement by phylogenetic trees

and its application to visual analysis of document col-

lections. In Proceedings of the 2007 IEEE Symposium

on Visual Analytics Science and Technology, pages

99–106. IEEE Computer Society.

Geng, X., Zhan, D. C., and Zhou, Z. H. (2005). Super-

vised nonlinear dimensionality reduction for visual-

ization and classiﬁcation. IEEE Transactions on Sys-

tems, Man, and Cybernetics, Part B: Cybernetics, 35

Issue:6:1098 – 1107.

Healey, B. G., Booth, K. S., and Enns, J. T. (1996). High-

speed visual estimation using preattentive processing.

ACM Transactions on Computer-Human Interaction,

3(2):107–135.

Ingram, S., Munzner, T., and Olano, M. (2009). Glimmer:

Multilevel mds on the gpu. IEEE Transactions on Vi-

sualization and Computer Graphics, 15(2):249–261.

Jolliffe, I. T. (1986). Pincipal Component Analysis.

Springer-Verlag.

Li, J. and Wang, J. Z. (2003). Automatic linguistic indexing

of pictures by a statistical modeling approach. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 25(9):1075–1088.

Mayorga, A. and Gleicher, M. (2013). Splatterplots:

Overcoming overdraw in scatter plots. IEEE Trans-

actions on Visualization and Computer Graphics,

TBD(TBD):TBD. Accepted, To Appear.

Paiva, J., Florian, L., Pedrini, H., Telles, G., and Minghim,

R. (2011). Improved similarity trees and their ap-

plication to visual data classiﬁcation. IEEE Trans-

actions on Visualization and Computer Graphics,

17(12):2459–2468.

Paulovich, F. V., Nonato, L. G., Minghim, R., and Lev-

kowitz, H. (2008). Least square projection: A fast

high-precision multidimensional projection technique

and its application to document mapping. IEEE

Transactions on Visualization and Computer Graph-

ics, 14(3):564–575.

Rensink, R. and Baldridge, G. (2010a). The perception of

correlation in scatterplots. Computer Graphics Forum

(Proceedings of EuroVis 2010), 29:1203–1210.

Rensink, R. and Baldridge, G. (2010b). The visual percep-

tion of correlation in scatterplots. Journal of Vision,

10(7):975.

Sedlmair, M., Tatu, A., Munzner, T., and Tory, M. (2012).

A taxonomy of visual cluster separation factors. Com-

puter Graphics Forum (Proc. EuroVis), 31(3):1335–

1344.

Tan, P. N., Steinbach, M., and Kumar, V. (2005). Intro-

duction to data mining. Addison-Wesley Longman,

Boston, MA, USA.

Tatu, A., Bak, P., Bertini, E., Keim, D. A., and Schnei-

dewind, J. (2010). Visual quality metrics and human

perception: an initial study on 2D projections of large

multidimensional data. In Proceedings of the Working

Conference on Advanced Visual Interfaces (AVI ’10),

pages 49–56.

Tenembaum, J. B., de Silva, V., and Langford, J. C. (2000).

A global geometric faramework for nonlinear dimen-

sionality reduction. Science, 290:2319–2323.

Ware, C. (2000). Information visualization: perception for

design. Morgan Kaufmann Publishers Inc., San Fran-

cisco, CA, USA.

Wertheimer, M. (2005). Untersuchungen zur lehre von der

gestalt. Psychological Research, 4:301–350.

RoleofHumanPerceptioninCluster-basedVisualAnalysisofMultidimensionalDataProjections

283