
Real-Time 3D Visualization of Accurate Specular Reflections in Curved
Mirrors
A GPU Implementation
Andr
´
e Lages Miguel, Ana Catarina Nogueira and Nuno Gonc¸alves
Institute for Systems and Robotics, University of Coimbra, Coimbra, Portugal
Keywords:
Three-Dimensional Graphics and Realism, Real-Time Rendering, Textures, Non-planar Reflections.
Abstract:
This paper presents a vertex-based solution for rendering real-time accurate reflections in quadric mirrors in
dynamic scenes using CUDA and OpenGL. Our method, based on forward projection, exploits the global
information of the vertices and textures as they are computed from its original positions, to their reflections
points in the mirror, and finally, to the eye. This solution does not suffer from parallax or visibility issues,
neither does it needs to deal with ray intersection. As viewers navigate through the scene, the reflection points
are instantly recalculated, depending on the position of the camera. Thus, given a 3D scene, this method
gathers all vertex, light, and texture information and computes them at every instance, finding the reflection
points and rendering the reflections on the mirror surface. We also demonstrate the accuracy and performance
of our method by rendering two sample scenes.
1 INTRODUCTION
Rendering non-planar reflections at real-time speed
has been a real challenge since the render-to-texture
technology and other recent advances became avail-
able in computer graphics. Although faking reflec-
tions in environment maps have been widely used as
a solution to render reflections in real-time (Blinn and
Newell, 1976), (Greene, 1986), (Haeberli and Segal,
1993), (Voorhies and Foran, 1994), the human eye
perceives what is wrong in a 3D scene. If a reflection
is fake, the user will easily notice. Recent games of-
fer fast and dynamic graphics that are close to photo-
realistic, however, the computational cost of drawing
a physically possible reflection in a non-planar mirror,
even using GPU parallelism, is still very high.
Although techniques have been used to render per-
fect reflections using raytraced systems ((D. Roger,
2007),(Parker et al., 2010)) or using cubemapped or-
thogonal views to a sphere ((Roger and Holzschuch,
2006), (Estalella et al., 2006), (Estalella et al., 2005))
such methods do not apply to our projection model.
Despite the growth of ray tracing capability and per-
formance through time, ray tracing is not suitable for
forward projection using non-central catadioptric sys-
tems, moreover, the rendering of efficient complex
dynamic scenes via ray tracing in real-time is still a
difficult task.
For this paper, we rendered a 3D scene where
the accurate reflection point for each vertex, at ev-
ery instance, is projected in a curved mirror. Our
rendering workflow is vertex-based and the reflection
is generated by connecting fans of textured triangles
that correspond to vertices in virtual objects in the
scene. Virtual objects are clones of the original ob-
jects, but finely tessellated (the closer to the reflec-
tor, the higher the tessellation is). These objects are
only rendered during the reflection and their vertices
are only used to find the reflection points. The idea
of our method when handling with dynamic scenes,
is that after the pre-processing stage, it only needs to
account for camera position and animated vertices to
render a complete reflection. We address the problem
of estimating the reflection point that belongs to the
surface of the mirror where light is projected from a
3D point in the direction of the camera (forward pro-
jection), which is similar to the ray casting system.
We thus present a novel approach to the compu-
tation and rendering singular-bounced reflections in
quadric mirrors which is unique in finding accurate
reflection points at a good speed. Additionally, to
prove the usefulness of our approach, we built an in-
teractive development kit for toys and particles, so
that in 3D scenes containing a reflector, objects can
be added and animated. The reflectors that are ad-
dressed by our method are quadric shaped (spheres,
136
Lages Miguel A., Nogueira A. and Gonçalves N..
Real-Time 3D Visualization of Accurate Specular Reflections in Curved Mirrors - A GPU Implementation.
DOI: 10.5220/0004691901360143
In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (GRAPP-2014), pages 136-143
ISBN: 978-989-758-002-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

ellipsoids, paraboloids and hyperboloids). We intro-
duce a method that computes only the most relevant
vertices at each frame to maintain visual accuracy and
save computational costs.
Our main contributions are: the speed of our al-
gorithm rendering a full scene with accurate reflec-
tions in curved mirror (the parallelism, possible due
to vertex independence, allows the GPU to perform
searches for many vertices at the same time); the time-
saving operations made to the algorithm to main-
tain the reflection accuracy with reduced computa-
tional power - the CPVV - which is an approach that
only computes the most important vertices and dis-
card the other ones to preserve reflection accuracy,
and a Painter’s Algorithm approach regarding vertex
occlusion.
2 RELATED WORK
Blinn and Newell introduced Environment and
Sphere Mapping techniques to fake specular reflec-
tions. These methods (Blinn and Newell, 1976) can
speed up a curved reflection, however, the reflection
is inaccurate and may suffer from parallax issues. For
faking reflections, an alternative is the Image-Based
Lighting proposed in (Bjorke, 2004), which consists
in adding shader calculations, for placing objects in-
side a reflection environment of a specific size and lo-
cation. This technique provides higher quality, how-
ever, it does not solves parallax issues at low distance
from the reflector.
Accelerated ray tracing methods have been im-
plemented on the GPU to compute specular reflec-
tions with good performance, though it only suits
non-dynamic scenes (Purcell, 2004). (Ofek and Rap-
poport, 1998) also proposed an interesting solution
for rendering interactive reflections on curved objects.
For every vertex in the scene, an explosion map ac-
celerates the search for a triangle used to perform
the reflection. This solution is efficient, but has mi-
nor artifacts. In (Szirmay-Kalos et al., 2005) a ray
tracing based method that achieves real-time speed is
proposed for curved mirrors, yet, when dealing with
poorly tessellated objects lacks of accuracy in the re-
flection. ((Estalella et al., 2005), (Estalella et al.,
2006), (Roger and Holzschuch, 2006)) proposed an
interesting cube-mapped based method for very ac-
curate reflections intended for pinhole cameras. The
vertices in the scene are computed to pre-processed
cube maps around the mirror, but again, it fails to be
accurate when the objects in the scene are poorly tes-
sellated. Other techniques have shown the use of tex-
ture maps to build and draw reflections, with the aid
of OpenGL (McReynolds et al., 2000). More accu-
rate methods have already dropped the use of envi-
ronment mapping and stepped into ray traced meth-
ods. The most important, but not suitable for forward
projection, is Optix (Parker et al., 2010), a ray tracing
engine for highly parallel architectures.
Ray tracing is an inherently parallel technique but,
despite this fact, the shared memory management is
difficult, mainly if an efficient GPU implementation
is aimed, since it is primarily designed for stream-
ing polygon rasterization (Purcell, 2004). As men-
tioned by (Wald et al., 2003), (Woop et al., 2005),
(Carr et al., 2006), since most ray tracing algorithms
use pre-processed acceleration data structures (for
static models), ray tracing is not suitable for dynamic
scenes.
Dynamic environments can be treated combin-
ing pre-computation and warping (Meyer and Loscos,
2003), and they can also be used to compute recur-
sive specular reflections (Hoy et al., 2002). The above
methods do not provide satisfactory results when the
viewer is close to the reflector too.
On another hand, the GPU availability to carry ex-
tra workload closes an huge set of shading and light
limitations, increasing the dynamism and realism in
modern games. Accurate specular reflections are be-
coming a widely common effect in fully dynamic
scenes. Thus, as mentioned above, the use of envi-
ronment mapping methods is decreasing over time,
meaning that if a dynamic scene has to be as real as
possible in real-time, is easier to use a multipass tech-
nique rather than pre-compute data.
Most of the techniques to trace the light path rely
on pixel and rays computations, and depend on global
geometry approaches to handle the reflection. The
computational cost for rendering a reflection grows as
complex illumination and dynamic effects are added,
so as with ray intersection and glossy highlights. The
use of geometry/vertex and pixel shader have been
widely used to render reflections. Usually, the vertex
program estimates a triangle for the projection region
and the fragment shader renders the projection region
out of the bounding triangle. Such method is easy to
compute and provides good results, however, is diffi-
cult to implement using our projection model.
Nonlinear Beam Streaming on the GPU has been
proposed and used as a reliable competitor with ray-
tracing (Liu et al., 2011). This approach is based
on polygon rasterization and produces fast and ac-
curate results at rendering nonlinear global illumina-
tion effects such as curved mirror reflection, refrac-
tion, caustics, and shadows. This method proves to
be more suitable than raytracing when handling with
dynamic scenes.
Real-Time3DVisualizationofAccurateSpecularReflectionsinCurvedMirrors-AGPUImplementation
137
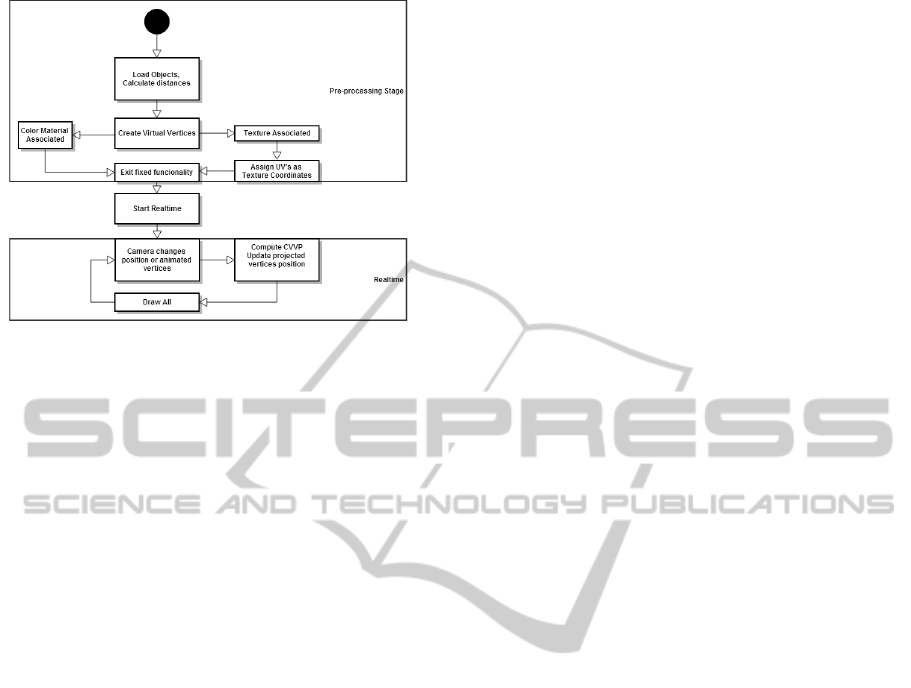
Figure 1: Diagram of our algorithm, from the pre-
processing stage to the realtime calculations stage.
3 ALGORITHM OVERVIEW
In the diagram of figure 1 we summarize our algo-
rithm pipeline.
Initially, all static meshes are loaded and the po-
sition of each vertex is stored for immediate dis-
tance calculations. Virtual objects are created for ev-
ery loaded mesh and the tessellation level given to a
virtual object depends on the distance to the mirror.
Since every virtual mesh is divided in simple geome-
tries, one virtual object may have different tessellation
levels, the created virtual objects will be invisible, but
the virtual vertex information will be used to compute
high order reflections. In this pre-realtime stage, tex-
ture information must be assigned to the vertices of
the mirror, so that when realtime begins, the minimal
amount of information is needed to compute and ren-
der a full reflecting sphere. If an object has a texture
associated to it, the same texture ID is linked to the
reflection vertices that represent that mesh. A simi-
lar process is used to link color and light information
to the reflection points if the matching virtual vertices
have no texture. To enhance performance, all of the
vertex data that compose the reflector is stored in high
performance graphics memory. To reduce the number
of function calls, no pixel data is needed.
Thereafter, after all static data is processed, the re-
altime calculations begin - the environment is quickly
drawn and the mirror is ready to reflect the objects.
Upon camera movement, the new position values for
the camera are sent to the projection functions that
will estimate the new reflection points, at that time
several vertices are computed simultaneously, using
the GPU for arithmetic operations and the CPU for
the remaining actions to estimate the new values for
the reflection vertices. Not all existing virtual vertices
are computed at each frame as, as we explain later,
our method can choose to compute only the most im-
portant vertices to safeguard visual accuracy.
For each virtual mesh vertex we then compute a
reflection point, based on the actual camera position.
Under this representation, each mesh vertex can be
considered an independent thread that allows for other
vertices to be projected at the same time.
3.1 Pre-Realtime
In this algorithm, we first render the lightmaps of the
geometry with proper illumination, these lightmaps
will be used as textures in the reflector - this is done
in an offline step. Access to texture memory is op-
timized in a CUDA kernel, so it does not delay the
program execution and avoids the traditional graph-
ics pipeline fixed-function limitations. The vertices
positions are then copied onto the GPU during the
initialization step. The 3D scenes presented in this
paper has dynamic lighting and shadowing applied.
Also, the static objects are textured with precomputed
lightmaps, which suffer from some direct illumina-
tion from the dynamic lighting. At this point, no
projections to the reflector were already calculated,
running at approximately 644 fps with a low-polygon
scenario. Although dynamic lighting is applied to the
objects, the light contribution in the reflector may suf-
fer variations if the objects are extremely exposed to
a light source. Before the context is created, the data
that describes the scene is extracted and labeled so
that, at the time of the reflection points calculations,
each vertex of the reflector is already associated with
a position in a texture and with nearby vertices.
Our algorithm handles low-polygon and well tes-
sellated objects. In the case of low-polygon meshes,
a virtual object for this mesh will be created - as ex-
plained before, the virtual object associated to a mesh
will divide it into finely tessellated simple geometries
with n vertices and afterward these virtual vertices po-
sitions are stored in VBOs. For every vertex stored,
a set of values is associated to it: a 2D coordinate is
stored in shared memory in a buffer with all necessary
Texture Coordinates useful for reflecting textures and
an id of the mesh and division associated to the vertex,
and consequently, to a texture.
In this paper we implemented a novel method that
only computes a few necessary points at each frame.
In order to reduce the computation workload, at ev-
ery frame, only the borders of a virtual object will be
projected onto the mirror. The virtual vertices with
less then four neighbors are labeled as CPVV (Con-
stantly Projected Virtual Vertices). While the CPVV
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
138

points are computed and projected at each frame, the
remaining vertices are drawn as a triangle fan with N-
2 triangles, being N = VertexCount - CPVVCount. By
applying this process, only the most imperative ver-
tices that guarantee the visual accuracy of the reflec-
tion are computed at each frame, however at a close
range from the reflector, artifacts can be seen, such as
discontinuities in parts of the reflection. To improve
performance, this function has a tunable value that
defines if the non CPVV points are to be projected
less often, or more often for better quality. The stage
of choosing the adequate points to be CPVV happens
right after the virtual objects creation, thus providing
enough data to begin the realtime application, where
the algorithm now only needs to account for camera
and animated vertices positions. This smart allocation
of computational resources produces gains in perfor-
mance when rendering in real-time. In order to guar-
antee fast access to vertex data, all animated objects
have their vertex positions updated in the same mem-
ory space as the CVPP, since these points will be con-
stantly projected, even upon camera movement.
3.2 Projection Model
The Forward Projection Model used in our render-
ings is based on the Quadric Intersection Method
presented by Goncalves (Goncalves, 2010) and
Goncalves and Nogueira (Goncalves and Nogueira,
2009). The three main inputs are:
• 1) a quadric surface reflector, defined by the fol-
lowing quadratic equation:
x
2
+ y
2
+ Az
2
+ Bz −C = 0 (1)
where the coefficients A, B and C are arbitrary
scalars. This parameterization of the quadric
mirrors comprises rotationally symmetric mirrors
such as spherical, parabolic, hyperbolic and ellip-
tic. The quadric mirror can also be expressed by
a quadric matrix Q, in homogeneous coordinates,
such that the point x =
x y z 1
T
belongs
to quadric Q if and only if respects the equation
x
T
Qx = 0.
• 2) the camera center of projection (COP), which
is considered to be placed at the point COP =
c
x
c
y
c
z
1
T
• 3) and the 3D point to be projected (object point),
that is defined as P =
X Y Z 1
T
.
As illustrated in figure 2 the incident ray intersects
the reflector surface at the reflection point R, where
the light ray is projected to the camera along the re-
flected direction.
Figure 2: Reflection through a quadric reflector where the
reflection point is searched in a parameterized quartic curve
R(λ).
As stated by the Quadric Intersection Method
((Goncalves, 2010) and (Goncalves and Nogueira,
2009)) an additional constraint on the reflection point
is imposed, allowing a much faster way to search for
the reflection point. This constraint imposes that the
reflection point belongs not only to the reflector sur-
face but also belongs to an analytical quadric, whose
expression depends exclusively on the geometry of
the projection (center of projection and 3D point to
be projected). Since the searched reflection point
belongs to these two quadrics, it shall be searched
in their intersection, which has only one dimension.
This characteristic turns the method much faster than
other reflection methods like Law of Reflection or
Fermat Principle.
As proved in (Goncalves, 2010), the parametric
curve given by the intersection algorithm is a function
of only one parameter, say λ. Although nonlinear, the
curve can be searched for the point where the total
distance traveled by the light is minimum, stated by
the Fermat Principle.
Therefore, the reflection point R belongs to the
quadric reflector Q and also to the analytical quadric
S, whose expression is given by (Goncalves, 2010):
S = M
T
Q
∗
∞
Q + Q
T
Q
∗
∞
M (2)
where the matrix Q
∗
∞
is the absolute dual quadric and
M is a skew-symmetric matrix that depends on the
center of projection of the camera and the 3D point to
be projected. M is expressed by:
M =
0 c
z
− Z −c
y
+Y c
y
Z − c
z
Y
−c
z
+ Z 0 c
x
− X −c
x
Z + c
z
X
c
y
−Y −c
x
+ X 0 c
x
Y − c
y
X
−c
y
Z + c
z
Y c
x
Z − c
z
X −c
x
Y + c
y
X 0
(3)
For the general case, the parameterization ob-
tained involves the solution of a polynomial up to the
8th degree.
Another method for the computation of the reflec-
tion point through curved mirrors, and also using for-
ward projection, was proposed by Agrawal, Taguchi
and Ramalingam (Agrawal et al., 2011). Although
Real-Time3DVisualizationofAccurateSpecularReflectionsinCurvedMirrors-AGPUImplementation
139

both methods are presented as a problem of solving an
8th degree polynomial, our preliminary experiments
showed that the Quadric Intersection Method has bet-
ter performance than the former one. Both methods
can, however, be used in our algorithm to render ac-
curate reflections in quadric mirrors.
4 DETAILS OF THE
ALGORITHM
We here present the details of our algorithm by ren-
dering two different game environment scenarios run-
ning at an average speed of 143 fps. The first testing
environment is a room filled with toys with different
shapes and the other scene is a well lit corridor.
The Quadric Intersection Method ((Goncalves,
2010) and (Goncalves and Nogueira, 2009)) that finds
the reflection points is now implemented on the GPU,
using OpenGL interopability with CUDA on an Intel
Core i7 3.4GHz with a GeForce GTX680 card.
In this section we start detailing our approach.
Our approach is based on approximating the reflec-
tor by a polygonal mesh stripped with triangles. Be-
fore dealing directly with the reflection, our algorithm
scans the scene for every object, creating virtual ver-
tices and labeling the most important ones for perma-
nent reflection, as explained in section 3.
4.1 Parallel Computation
During run time, the virtual vertices to be computed
do not rely on other vertices. This independence al-
lows the program to GPU parallelism. Because the
point projections are drawn with triangles, after at
least three vertices are projected, the algorithm only
needs one point to draw a new triangle. The new ver-
tex is indexed to the other two previously vertices that
already share a triangle with another vertex. Using
this method we ensure that all vertex positions are up-
dated fast enough when rendering a new frame.
The program calls parallel kernels (simple func-
tions that make arithmetic operations) - so that the
kernel executes in parallel across a set of other par-
allel threads. A streaming of virtual vertices is thus
a thread block - a set of concurrent threads that can
cooperate among themselves through barrier synchro-
nization and shared access to a memory space private
to the block. In this context, a virtual object in the
scene is programmed as a grid, i.e. a set of thread
blocks (vertices) that may be executed independently
and thus may execute in parallel. Since the algo-
rithm to find the reflection points is actually a bunch
of arithmetic operations, the kernel is called to per-
form the majority of the operations. Particularly, each
thread checks if the corresponding vertex satisfies the
given properties to be later projected, and if so, it sets
the value representing the property for all immediate
successors of the vertex.
As for the algorithm performance, it is limited
by memory bandwidth since, for each vertex update,
only few instructions are executed. The quadric inter-
section method used to find the reflection points is a
straightforward set of hierarchical operations depen-
dent on each other. Calling the CUDA kernel ensures
that all arithmetic operations as computed in parallel
for several vertices.
Upon the static data is processed, the context is
created and the real-time calculations begin while the
scene is rendered. At each frame, the position of the
camera is updated and accountable for calculations,
and the static objects are drawn. If the CPVV is en-
abled, the rendering will speed up and the most no-
ticeable and animated vertices will be drawn to main-
tain visual accuracy.
For convenience, the render of the reflection is the
last one to be drawn. The rendering stage begins with
no updated information about the reflected vertices
coordinates, which happens while the objects are be-
ing rendered. This is not considered to be a two-pass
rendering, but as a single render pass that suffers from
an extremely small standby, while switching to fixed
functionality to execute the last operations to find the
reflection points.
4.2 Vertex Independence
The projection method used in this paper is based
on a geometric cost function minimization, there-
fore, the projection of a point is accurate and inde-
pendent of the remainder scene, only using the sur-
rounded information for the tessellation step. The
output of our application is a mirror surface that re-
flects a whole scene, built with vertices connected by
a fan of textured triangles, after the first frame the re-
flection points positions are updated and translated.
At the end of the first instance, every virtual vertex in
the scene has a reflection point associated to it, that
is a vertex position with a constant 2D texture coor-
dinate or a rgb color in the case of no texture asso-
ciation. After that, during the execution time of the
visualization, each virtual vertex is always connected
to the same reflection point.
All projected vertices are stored in VBO’s. The
algorithm used to create virtual objects divides an ob-
ject in simple polygons, if possible. Simple meshes
like planes and cubes are easier to deal with - as an
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
140

example, if a low-polygon cube mesh with eight ver-
tices is loaded to the scene, the algorithm will divide
it in six planes and assign virtual vertices to each one
depending on their position relatively to the reflector.
In a relatively far distance from the mirror, a plane
would be divided in a 4x4 grid with 25 vertices and
32 triangles. If the same plane is closer to the reflec-
tor, it will have a larger vertex and triangle count.
4.3 Rendering
The rendering process counts on polygon rasteri-
zation and texture/color fetch, leaving the GPU in
charge of drawing everything, where the GPU proves
to be well suited for streaming polygon rasterization,
instead of pixel/ray computations. Our algorithm
deals easily with the streaming of particle systems.
Each particle is accountable as a vertex in 3D space.
The reflection of particles is drawn as a 3D texturized
polygon, exactly like the drawing in the 3D space,
keeping the algorithm simple and able of rendering
dynamic effects.
As explained earlier, to avoid a double rendering
pass and improve the performance, the calculation of
the reflection points is done at the same time of the
scenario rendering. Thus, when the camera position
changes, vertices are computed and the only element
that is updated is the position of the reflection points
on the mirror, as the assignment of texture coordinates
remains the same. Finally, the reflection points are
stripped on reflector with small textured triangles.
As mentioned in the introduction, the examples in
this paper combine OpenGL and CUDA. The use of
such tools facilitate the minimization of communica-
tions across the PCIe bus and speeds up the rendering
time, enabling primitive restart, drawing primitives
such as triangle fans or strips that only use textures.
4.4 Occlusions
An approach based on the Painter’s algorithm handles
all visibility issues in our application. The visual ap-
pearance of the mirror upon rendering shows an im-
perceptible layer of small triangles connected by ver-
tices, however, not all of these vertices are connected.
The projected triangles from closer objects, being
highly tessellated, fill the respective space in the re-
flector, thus occupying a larger diameter and covering
hidden spaces of other objects. When the distance be-
tween reflections of different objects is very small, the
projected points are all computed regarding the same
value for the mirror geometry (namely the radius),
however, by using this Painter’s algorithm based ap-
proach, the reflection of closer objects to the reflec-
tor will have their reflection point positions multiplied
by a very small value. When handling with a finely
tessellated scenario containing very complex meshes,
small artifacts are visible with camera proximity to
the mirror. For convenience, the objects nearest to the
reflector are drawn last, overlapping the reflection of
distant objects.
4.5 Limitations
As for the limitations of our approach, we identified
some issues to be addressed. Our rendering method
suffers from a speed loss at a point of the workflow,
when the scene is overly tessellated (over 12000 ver-
tices or 5000 CPVVs). When adding a new object to
the scene, its rendered reflection will, at least, last 24
frames to appear on the reflector surface. This hap-
pens due to the fact that a virtual object has to be cre-
ated for the new added one. So the algorithm has to
fetch his textures and vertex positions in order to input
this object in the real-time calculations and rendering.
However, if the object is animated, the rendered re-
flection will not have a noticeable latency.
Another limitation is the computation of unneces-
sary points, due to occlusion issues. Occluded ver-
tices to the reflector are computed as well, despite of
being invisible and the self occluded part of the reflec-
tor is computed and projected as wel, even with the
CPVV method enabled. This problem will be solved
in the near future with a different approach to invisi-
ble vertices.
Finally, another limitation that will be addressed
in the future, is the non-reflection of animated dy-
namic shadows. This means that, if a new animated
object is added to the scene, the shadow will not be
considered as reflection, only the object will be pro-
jected. In a near future we will deal with this lim-
itation with the creation of virtual shadows for each
new object. Still, the rendering process is reasonably
faster with no dynamic lighting applied.
Figure 3: The left image shows a close-up view from the
surface of the mirror reflecting a streaming of particles. Due
to the particles proximity to the mirror, the reflected parti-
cles do not belong to the surface of the mirror. On the other
hand, the image on the right shows that, from a distant cam-
era position, yet, still a close view, the particles reflection
have no visible artifacts.
Real-Time3DVisualizationofAccurateSpecularReflectionsinCurvedMirrors-AGPUImplementation
141

Figure 4: The image on the left shows one of the created environment (a room with toys) and, at the center, its reflection on the
surface of the mirror, projecting 7400 CPVVs, running at 61 fps. The image on the right represents an ancient environment,
running at 200 fps for 7500 vertices.
In future work, we intend to rebuild the render-
ing pipeline with multipass in order to test possible
performance and quality gains. By rendering a singu-
lar pass, the CUDA/OpenGL interopability uses asyn-
chronous mapping of a buffer within a stream of vir-
tual vertices, allowing the rendering to be extremely
fast, giving no need for another render pass.
5 RESULTS
We present the results of our approach for two differ-
ent scenes: one representing a room filled with toys,
the other representing an ancient environment (Figure
4). The frame rates (indicated at each image legend)
may arise if the CPVV mode is enabled. The images
below show renders computed using our method after
finding the reflection points for every virtual vertex
in the scene. When the CPVV is enabled, only 25%
of the virtual vertices are computed at every frame,
where the remaining ones wait for considerable cam-
era movements to be computed again. This technique
thus highly accelerates the renderings. For reference
purposes, we simulated the same ancient environment
with ray tracing with no real-time speed.
The results of our method show that, when han-
dling with complex scenes with dynamic effects, the
reflection up to 15000 points will guarantee real-time
frame rates and a higher image quality. The tessel-
lation level assigned to the virtual objects is scal-
able and easily adaptable to other scenes. Figure 6
shows our algorithm reflecting several objects at 49
fps. Also, the CPVV is enabled and is responsible
for only computing important vertices. Upon signif-
icant camera movement, the remaining vertices will
also be computed - at this time, the frame rate will de-
crease to near real-time speed until the projection of
these points is completed and at that time the frame
rate will increase again.
When comparing our method to the ray traced ref-
erence (Figure 5), the visual aspects look very similar,
although, the raytraced image took 12 seconds to ren-
Figure 5: The upper image is a raytraced reference obtained
with a rendering engine. The bottom one was rendered with
our algorithm and runs at 203 fps, projecting 1200 vertices.
Figure 6: Room filled with toys rendered using our projec-
tion model, projecting 10000 vertices at 49 fps.
der while the image rendered with our method was
running at 203 fps. However, small artifacts can be
seen using our method by zooming the image, such as
some straight lines that should be a curve of the reflec-
tor. These artifacts may be visible when the scene is
not well tessellated (only 1200 vertices on this case).
Nevertheless, the overall quality of the image is suffi-
ciently good and extremely fast.
GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications
142

6 CONCLUSIONS AND FUTURE
WORK
Our approach is simple and nearly perfectly accurate
for real reflections. It organizes and simplifies the
data to be projected and its computation, in a way
which makes excellent use of GPU parallelism. The
reflection on the mirror surface is flickering-free and
highly tessellated, the pre-computation phase is also
fast and almost only depending on texture fetching.
The experiments show that our method provides
very similar results to ray tracing and GLSL ap-
proaches, with real-time performance and real reflec-
tion accuracy. Furthermore, the algorithm speeds up
rendering, taking advantage of GPU parallelism, al-
lowing users to tune the accuracy of the reflections.
As an outcome, our approach is favorably fast and
produces fine results.
In terms of limitations, our algorithm requires a
reasonable amount of preprocessing before rendering
a scene on the reflector. Also, we do not deal with
occlusions as it is usually done, using any kind of
buffer. When computing the reflection, the farther
objects to the reflector are computed and drawn first.
We strongly believe that these limitations can be over-
come in the near future. Despite the results were not
as fast as cube-mapped techniques, the accuracy in
our method is always proper with objects at any range.
Future directions include to further optimize the
computation of the forward projection model solu-
tion. In the field of graphics we intend to test these
methods and compare them in the rendering of im-
ages with specular objects represented by arbitrary
surfaces that could be approximated by quadrics. We
also intend to implement our method entirely on the
pixel shader to test performance gains.
REFERENCES
Agrawal, A., Taguchi, Y., and Ramalingam, S. (2011). Be-
yond alhazen’s problem: Analytical projection model
for non-central catadioptric cameras with quadric mir-
rors. In IEEE CVPR.
Bjorke, K. (2004). Image-based lighting. In NVidia, editor,
GPU Gems, pages 307–322.
Blinn, J. F. and Newell, M. E. (1976). Texture and reflec-
tion in computer generated images. Commun. ACM,
19(10):542–547.
Carr, N., Hoberock, J., Craneh, K., and Hart, J. (2006). Fast
gpu ray tracing of dynamic meshes using geometry
image. In Proceedings of Graphics Interface 2006.
D. Roger, U. Assarsson, N. H. (2007). Whitted ray-tracing
for dynamic scenes using a rayspace hierarchy on the
gpu. Eurographics Symposium on Rendering.
Estalella, P., Martin, I., Drettakis, G., and Tost, D. (2006).
A gpu-driven algorithm for accurate interactive spec-
ular reflections on curved objects. In Eurographics
Symposium on Rendering, pages 313–318.
Estalella, P., Martin, I., Drettakis, G., Tost, D., Devilliers,
O., and Cazals, F. (2005). Accurate interactive specu-
lar reflections on curved objects. In Vision, Modeling,
and Visualization - VMV.
Goncalves, N. (2010). On the reflection point where light
reflects to a known destination in quadric surfaces.
Optics Letters, 35(2):100–102.
Goncalves, N. and Nogueira, A. C. (2009). Projection
through quadric mirrors made faster. In ICCVW: 9th
Workshop on Omnidirectional Vision, Camera Net-
works and Non-Classical Cameras, Kyoto, Japan.
Greene, N. (1986). Environment mapping and other ap-
plications of world projections. In IEEE Computer
Graphics and Applications, volume 6.
Haeberli, P. and Segal, M. (1993). Texture mapping as
a fundamental drawing primitive. In Fourth Euro-
Graphics Workshop on Rendering, pages 259–266.
Hoy, K., Niels, N., Christensen, J., and Informatics (2002).
Real-time recursive specular reflections on planar and
curved surfaces using graphics hardware. Journal of
WSCG, 10(3):91–98.
Liu, B., Wei, L.-Y., Yang, X., Ma, C., Xu, Y.-Q., Guo, B.,
and Wu, E. (2011). Non-linear beam tracing on a gpu.
Comput. Graph. Forum, pages 2156–2169.
McReynolds, T., Blythe, D., Grantham, B., and Nelson, S.
(2000). Advanced graphics programming techniques
using OpenGL. SIGGRAPH 2000 Course 32.
Meyer, A. and Loscos, C. (2003). Real-time reflection on
moving vehicles in urban environments. In VRST’03:
Proceedings of the ACM symposium on virtual reality
software and technology, pages 32–40.
Ofek, E. and Rappoport, A. (1998). Interactive reflections
on curved objects. In SIGGRAPH’98, pages 333–342.
Parker, S. G., Bigler, J., Dietrich, A., Friedrich, H., Hobe-
rock, J., Luebke, D., McAllister, D., McGuire, M.,
Morley, K., Robison, A., and Stich, M. (2010). Optix:
A general purpose ray tracing engine. ACM Transac-
tions on Graphics.
Purcell, T. J. (2004). Ray Tracing on a Stream Processor.
PhD thesis, Department of Computer Science, Stan-
ford University, Stanford, CA.
Roger, D. and Holzschuch, N. (2006). Accurate specular
reflections in real-time. Computer Graphics Forum,
25(3):293–302.
Szirmay-Kalos, L., Aszodi, B., Lazanyi, I., and Premecz,
M. (2005). Approximate ray-tracing on the gpu with
distance impostors. In Computer Graphics Forum
(Proceedings of Eurographics 2005), volume 24.
Voorhies, D. and Foran, J. (1994). Reflection vector shading
hardware. In SIGGRAPH’94.
Wald, I., Benthin, C., and Slusallek, P. (2003). Distributed
interactive ray tracing of dynamic scenes. In IEEE
Symposium on Parallel and Large-Data Visualization
and Graphics, pages 11–20.
Woop, S., Schmittler, J., and Slusallek, P. (2005). A pro-
grammable ray processing unit for realtime ray trac-
ing. In ACM Transactions on Graphics.
Real-Time3DVisualizationofAccurateSpecularReflectionsinCurvedMirrors-AGPUImplementation
143
