Kinetic Equation Method and Monte Carlo Method for Charge
Carriers Dynamics Description in Diamond
Yu M. Belousov, I. V. Chernousov, V. R. Soloviev and I. A. Varfolomeev
Moscow Institute of Physics and Technology, 141700, Insitutskij per., 9, Dolgoprudniy, Moscow Region, Russia
Keywords: Charge Carriers, Acoustic Phonons, Mobility, Kinetic Equation Method, Monte Carlo Method.
Abstract: In this work charge carriers mobility in diamond, calculated by two means – by kinetic equation method and
by Monte Carlo method – is analyzed. Temperature of diamond crystal less than 300 K and low
concentration of impurities are considered, therefore carriers are scattered preliminary by acoustic phonons.
Electron-phonon interaction is taken in deformation potential approximation. Phonon emission and
adsorption rates are calculated and Monte-Carlo method is used to obtain carriers mobility. The mobility is
compared with that obtained by kinetic equation method in our previous work. The results are important for
the treatment of electrical experiments in pure monocrystalline diamonds.
1 INTRODUCTION
At temperatures below 300 K and sufficiently low
concentration of impurities and defects, the charge
carriers mobility in diamond is restricted
substantionally by scattering at acoustic phonons.
Over the years, the carrier mobility in diamond has
been measured many times as a function of
temperature for different types of this material
(Prelas et al., 1998; Nesladek et al., 2008; Isberg et
al., 2002; Pernegger et al., 2005; Pomorski et al.,
2007). Nevertheless, the temperature range below 80
K in pure diamond crystals has hardly been studied.
Even latest works with mobility studies deal with
rather impure samples, for example in (Jansen et al.,
2013) the order-of-magnitude estimate for the
concentration of neutral impurities was about 10
17
cm
-3
, what leads to mainly impurity mechanism of
scattering at temperatures lower than 100 K and so
impedes high carriers mobility. In view of good
prospects of diamond for design of electronic
devices with unique properties (Sussmann, 2009;
Isberg et al., 2012), particularly ionizing radiation
detectors, increasingly pure diamond single crystals
will be produced, carriers mobility at low
temperatures will be sooner or later measured in
them, and the interpretation of these experiments
will be an urgent problem.
Generally, the mobility is calculated within the
quasielastic approach, but this approach gives bad
accuracy in diamond due to high velocity of sound
(Baturin, 2010; Belousov, Soloviev, Chernousov,
2013). In these works the inelasticity was taken into
account by utilizing a not simplified collision
integral in the right part of kinetic equation in two-
moment approximation and in 0-dimensional or 1-
dimensional cases. The solution was based on the
numerical integration of the kinetic equation. If
necessary, this approach can easily be modified to
take into consideration a self-consistent electric
field, created by charge carriers. On the other hand,
this approach does not take into account quadrupole
and higher moments of distribution function, what
leads to discrepancies from exact solution. In order
to estimate the error of calculation, it is reasonably
to compare it with the results of Monte-Carlo
method simulation, what is implemented in this
work. Monte-Carlo method is favourable to analyze
kinetic processes with low concentration of charge
carriers, i.e., without self-consistent field, but its
advantage is possibility to conventionally solve 2-
and 3-dimensional problems.
2 FORMULATION OF THE
PROBLEM
2.1 Physical Model
In this work a model from (Baturin et al., 2010;
Belousov, Soloviev, Chernousov, 2013) of diamond
122
Belousov Y., Chernousov I., Soloviev V. and Varfolomeev I..
Kinetic Equation Method and Monte Carlo Method for Charge Carriers Dynamics Description in Diamond.
DOI: 10.5220/0004809801220126
In Proceedings of 2nd International Conference on Photonics, Optics and Laser Technology (PHOTOPTICS-2014), pages 122-126
ISBN: 978-989-758-008-6
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

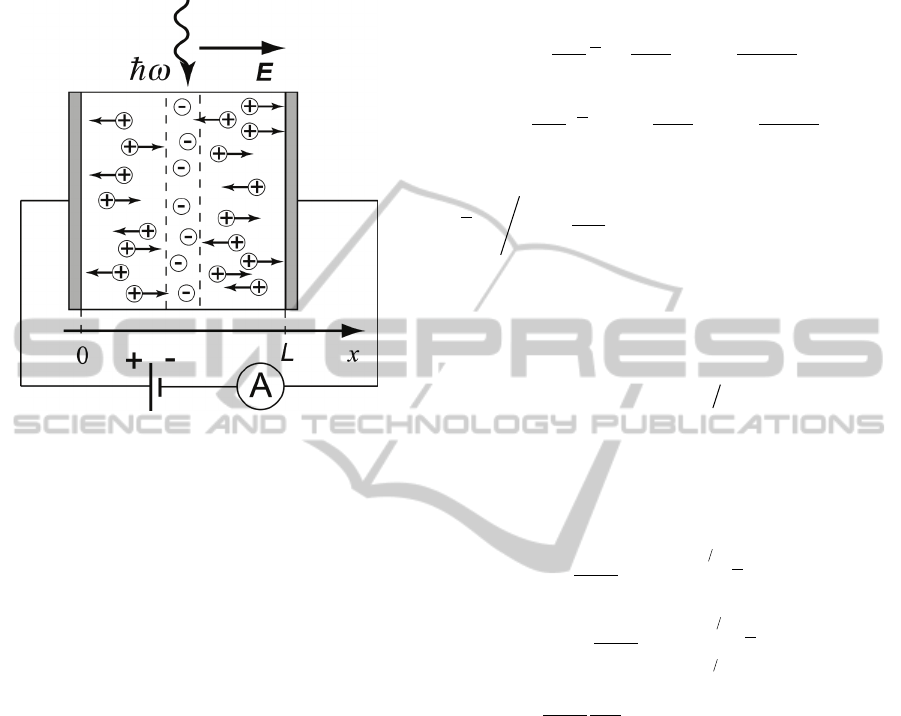
radiation detector consisting of thin plate, which
facets are covered by metal electrodes, linked to
power supply (fig. 1), is considered.
Figure 1. Physical model of diamond ionizing-radiation
detector.
The plate sizes are taken much larger than its
thickness – this allows to treat the system as one-
dimensional in the direction perpendicular to the
plates. Ionizing radiation creates electron-hole pairs
and ionize impurities. As in previous studies, to fix
the idea, the diamond is assumed to be doped with
boron atoms (acceptor, binding energy of a hole is
0.37 eV), the non-equilibrium carriers are generated
in a certain layer of the plate by laser radiation,
ionizing the impurities and the case of completely
permeable electrode-diamond contacts is considered
(the charge carrier, coming to the contact,
disappears). Charge carriers, moving into the
sample, induce electric current
in an external circuit
(Shockley-Ramo theorem). Parameters of ionizing
radiation can be determined from the pattern of
current versus time dependency and from the charge
traversed in an external circuit.
The concentration of impurities which generate
carriers, is assumed to be constant and independent
of how many carriers have been captured on them by
the given point of time.
2.2 Mathematical Model
In a pure monocrystalline diamond at temperatures
below 300 K, the main mechanism of charge carrier
scattering is scattering by acoustic phonons.
Following (Baturin et al., 2006; Varfolomeev,
Gorelkin, Soloviev, 2013), the probabilities of
absorption
−
Ω
and emission
+
Ω
of phonon by
charge carrier in deformation potential
approximation are respectively:
( )
2
2 22
2
q
qq
n cq
Mc m m
πδ
−

Ξ
Ω= − +






kq
,
(1
)
( )
( )
2
2 22
1
2
q
qq
n cq
Mc m m
πδ
+

Ξ
Ω= + + −






kq
,
(2
)
where Ξ is a deformation potential constant,
B
1 exp 1
q
sq
n
kT


= −






is the average number of
phonons with the wave vector q, M is the mass of
the crystal, m is the effective mass of the carrier, s is
the speed of sound in the crystal, T is the
temperature of the crystal, k
B
is the Boltzmann
constant,

is the Planck constant,
qs
is the
energy of the phonon,
22
2km ε = 
is the energy of
the carrier with wave vector
k
.
Hence the frequency of the emission
( )
e
k ν
and absorption
( )
a
k
ν
of phonons by the carrier can
be found:
( )
( )
( )
( )
max 0, 2 2
3
2
e
3
0
1
2
k ms
q
Vd
k n q dq
ν
π
−
+
=Ω=Ψ +
∫∫

q
,
(3
)
( )
( )
( )
22
3
2
a
3
max 0, 2 2
2
k ms
q
ms k
Vd
k n q dq
ν
π
+
−
−
=Ω=Ψ
∫∫


q
,
(4
)
here,
2
2
4
m
s
k
πρ
Ξ
Ψ=

,
ρ
is the density of diamond.
The total frequency (of carrier-phonon processes
and recombination) for carrier equals
( ) ( ) ( ) ( )
e a cap
kkk k νν ν ν =++
,
(5
)
where
( )
cap
k ν
is the frequency of carrier capture by
traps (if any).
In addition, carrier can get to the plate coating
and leave the volume of the plate.
2.3 Monte-Carlo Method Usage
In our case, the use of Monte Carlo simulation
consists in manifold independent simulation of
carrier dynamics. Carriers are generated
probabilistically in accordance with a specified
density of sources of carriers situated within the
sample. There are two competing processes – the
generation of new particles by the source and their
KineticEquationMethodandMonteCarloMethodforChargeCarriersDynamicsDescriptioninDiamond
123

capture by traps or leaving the sample. In the course
of time, a dynamic equilibrium between these
processes establishes (the number of "departures"
equals the number of "arrivals" in a unit of time),
and the average velocity of the carriers yields the
value of the mobility. Clearly, the average speed of
the carriers will give the less fluctuations over time
and hence the more accurate value of mobility, the
more particles there are in the sample in "stationary
state".
Any period of time of the free motion of the
carrier ends with one of the processes: emission of a
phonon, absorption of a phonon, capture of the
carrier by the trap or leaving the volume of the
sample.
The mean free time can be found by means of
expression (
5) for total frequency and by the
instrumentality of random number generator
(Mihailov, Voitishek, 2006):
( )
( )
1
ln 1 r
k
τ
ν
=−−
(6
)
where r is a random number with uniform
distribution on the interval [0,1].
The shift of the carrier along x axis during the
mean free time is calculated:
2
2
x
k
eE
x
mm
τ
τ
∆= +

,
(7
)
after that the test is done whether the carrier has
leaved the volume of the sample. If it has, than it
disappears and the program creates another carrier,
and so on until the necessary number of generated
carriers is obtained (100000 particles in our
calculation).
If the carrier hasn’t gone from the volume of the
sample, a process that aborted carrier’s motion in
electric field is drawn. When there aren’t any traps
in the sample, these processes can only be emission
and absorption of a phonon. Obviously, in this case
probabilities of emission or absorption are
respectively
( )
( ) ( )
e
ea
k
p
kk
ν
νν
+
=
+
and
( )
( ) ( )
a
ea
k
p
kk
ν
νν
−
=
+
(8
)
The magnitude of wave vector of absorbed or
emitted phonon is drawn with the use of cumulative
distribution function for emission (absorption) of
phonon with given wave vector:
( )
( )
( )
( )
( )
11
12
2
0
e
2
0
1
,
1
Lq
q
Lq
q
n q dq
F kq
n q dq
′
′
′′
+
=
′′
+
∫
∫
,
(9
)
where
( ) ( )
12
max 0, 2 2 ,L q k ms= − 
(10
)
( ) ( )
( )
( )
11 12
max 0, min ,L q L qq=
,
(11
)
( )
( )
( )
( )
( )
21
20
22
20
2
a
2
,
Lq
q
Lq
Lq
q
Lq
n q dq
F kq
n q dq
′
′
′′
=
′′
∫
∫
,
(12
)
where
( ) ( )
20
max 0, 2 2 ,L q ms k= −
(13
)
( )
21
22 ,L q k ms= + 
(14
)
( ) ( )
( )
( )
( )
22 21 20
max min , ,Lq LqqLq=
(15
)
Statistical sampling of
q
is conducted by
conventional formulae
( )
1
e
,q F kr
−
=
for emission
and
( )
1
a
,q F kr
−
=
for absorption of phonon
(inversion of the function is done for the second
argument). Scattering angle
χ
is found explicitly
from conservation laws and from the magnitude of
phonon wave vector, for emission process by
formulae
2
2
2
cos
2
ms q
kq
msq
kk
χ

−+


=
−


,
(16
)
for absorption process by formulae
2
2
2
cos
2
q ms
kq
msq
kk
χ

−−


=
+


(17
)
Azimuthal angle of a new direction of carrier
movement relative to initial direction is calculated as
random number, uniformly distributed on the
interval
[0; 2 ] π
.
2.4 Results of Simulation
Figure 2 shows the results of Monte Carlo
simulation in comparison with the results obtained
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
124

Figure 2: Results of Monte Carlo simulation in comparison with the mobility obtained by the kinetic equation method.
by the kinetic equation method (Baturin et al., 2010;
Belousov, Soloviev, Chernousov, 2013). The kinetic
equation method was taken in two-moment
approximation (Baturin et al., 2010) in isotropic and
one-dimensional versions, in quasi-elastic and
inelastic approximations.
Among these variants of the kinetic equation the
one-dimensional inelastic approximation seems to be
the most accurate. On the other hand, the Monte
Carlo method for the physical and mathematical
models described above should provide even more
accurate results because it is not simplified by two-
term approximation. Comparison of different
variants of the kinetic equation with the "exact"
results obtained
by the Monte Carlo method can be
used to assess the accuracy of the method of kinetic
equation. The value of mobility obtained by the
Monte-Carlo method at 90 K should be considered
as an overshoot due to a not large enough number of
particles accumulated. For the one-dimensional
inelastic approximation in the method of kinetic
equation almost equilibrium mobility values are less
than the Monte Carlo values at
30 KT <
and more
than it at
30 KT >
. The relative difference between
these mobilities is significant, up to 50%.
Interestingly enough that more rough version of the
kinetic equation method in the quasi-elastic isotropic
approximation gives mobility values closer to the
"exact" ones than the one-dimensional inelastic
variant, with the relative difference from “exact”
mobility up to 30%.
3 CONCLUSIONS
A comparison of the charge carriers mobilities
calculated using kinetic equation and using the
Monte Carlo method in diamond crystal at
temperatures less than 100 K and the absence of
impurities was performed. Carrier scattering is
mainly caused by acoustic phonons, the electron-
phonon interaction being taken in the deformation
potential approximation.
Results obtained by kinetic equation method in
two-moment approximation give a qualitatively
correct result, but, apparently, are not suitable for an
accurate enough quantitative description. The values
of mobility in the quasi-elastic approximation (“law
of 3/2”) at Т > 20 K differ from those obtained by
the Monte Carlo method no more than 30%. The
one-dimensional inelastic approximation in the
method of kinetic equation gives a result which
differs from the Monte Carlo method no more than
50%. At the same time it should be noted that the
kinetic equation method allows qualitative estimates
in the presence of the self-consistent field created by
charge carriers, what is complicated in the case of
the use of more precise Monte Carlo method.
KineticEquationMethodandMonteCarloMethodforChargeCarriersDynamicsDescriptioninDiamond
125

The obtained results yield assessments of the
accuracy of various approximations used for the
simulation of kinetic processes in diamond. This is
important both for choosing the correct method of
simulation of radiation detectors and other electronic
devices based on diamond, and for more accurate
definition of diamond charge carriers parameters by
experimental data.
REFERENCES
Prelas, M. A., Popovici, G., Bigelow, L. K. (Editors) 1998.
Handbook of Industrial Diamonds and Diamond
Films, Marcel Deccer, New York, pp. 377-412; p. 253.
Nesladek, M., Bogdan, A., Deferme, W., Tranchant, N.,
Bergonzo P. 2008. ‘Charge transport in high mobility
single crystal diamond’ Diamond and Related
Materials, vol. 17, pp. 1235–1240.
Isberg, J., Hammersberg, J., Johansson, E., Wikstrom, T.,
Twitchen, D. J., Whitehead, A. J., Coe, S. E.,
Scarsbrook, G. A. 2002. ‘High Carrier Mobility in
Single-Crystal Plasma-Deposited Diamond’ Science,
vol. 297, pp. 1670-1672.
Pernegger, H., Roe, H., Weilhammer, S., Eremin, P.,
Frais-Kolbl, V., Griesmayer, H., Kagan, E., Schnetzer,
H., Schnetzer, S., Stone, S., Trischuk, R., Twitchen,
W., Whitehead, D. 2005. ‘Charge-carrier properties in
synthetic single-crystal diamond measured with the
transient-current technique’ J. Appl. Phys, vol. 97, p.
073704.
Pomorski, M., Berdermann, E., Boer, W. De, Furgeri, A.,
Sander, C., Morse, J. 2007. ‘Charge transport
properties of single crystal CVD-diamond particle
detectors’ Diamond Relat. Mater., vol. 16, p. 1066.
Jansen, H., Dobos, D., Eisel, T., Pernegger, H., Eremin,
V., Wermes, N. 2013. ‘Temperature dependence of
charge carrier mobility in single-crystal chemical
vapour deposition diamond’ Journal of Applied
Physics, vol. 113, p. 173706.
Sussmann, R. S. 2009. CVD Diamond for Electronic
Devices and Sensors, Wiley, Wiley Series in Materials
for Electronic & Optoelectronic Applications.
Isberg, J., Gabrysch, M., Majdi, S., Twitchen, D. J. 2012.
‘Negative electron mobility in diamond’ Appl. Phys.
Lett., vol. 100, p. 172103-3.
Baturin, A. S., Gorelkin, V. N., Soloviev, V. R.,
Chernousov, I. V. 2010. ‘Calculation of the charge-
carrier mobility in diamond at low temperatures’
Semiconductors. vol. 44, no. 7, pp. 867-871.
Belousov, Yu. M., Soloviev, V. R., Chernousov, I. V.
2013. ‘Quasi-Elastic and Inelastic Approximations in
the Description of the Charge Carrier Dynamics in
Diamond’ Semiconductors, accepted for publication.
Baturin, A. S., Gorelkin, V. N., Rastunkov, V. S.,
Soloviev, V. R. 2006. Physica B., vol. 374–375, pp.
340–346.
Varfolomeev, I. A., Gorelkin, V. N., Soloviev, V. R. 2013.
‘Simulation of Charge Carriers Transport in Diamond
by Monte-Carlo Method’ Proceedings of MIPT (in
Russian), vol. 5, no. 3(19), pp. 139–153.
Mihailov, G. A., Voitishek, A. V. 2006. Statistical
simulation. Monte-Carlo methods, (in Russian),
Moscow, Publishing centre “Academy”, p. 368.
PHOTOPTICS2014-InternationalConferenceonPhotonics,OpticsandLaserTechnology
126