Decentralized Computation of Pareto Optimal Pure Nash Equilibria

of Boolean Games with Privacy Concerns

∗

Soﬁe De Clercq

, Kim Bauters

, Steven Schockaert

, Mihail Mihaylov

, Martine De Cock

and Ann Now´e

Dept. of Applied Mathematics, Computer Science and Statistics, Ghent University, Ghent, Belgium

School of Electronics, Electrical Engineering and Computer Science, Queen’s University, Belfast, U.K.

School of Computer Science and Informatics, Cardiff University, Cardiff, U.K.

Computational Modeling Lab, Vrije Universiteit Brussel, Brussels, Belgium

Keywords:

Boolean Games, Pure Nash Equilibria, Decentralized Learning.

Abstract:

In Boolean games, agents try to reach a goal formulated as a Boolean formula. These games are attractive

because of their compact representations. However, few methods are available to compute the solutions and

they are either limited or do not take privacy or communication concerns into account. In this paper we propose

the use of an algorithm related to reinforcement learning to address this problem. Our method is decentralized

in the sense that agents try to achieve their goals without knowledge of the other agents’ goals. We prove that

this is a sound method to compute a Pareto optimal pure Nash equilibrium for an interesting class of Boolean

games. Experimental results are used to investigate the performance of the algorithm.

1 INTRODUCTION

The notion of Boolean games or BGs has gained a lot

of attention in recent studies (Harrenstein et al., 2001;

Bonzon et al., 2006; Bonzon et al., 2007; Dunne et al.,

2008; Bonzon et al., 2012;

Agotnes et al., 2013). We

explain the concept of a BG with the following exam-

ple (Bonzon et al., 2006).

Example 1

Consider the BG G

with N = {1, 2, 3} the set of

agents and V = {a, b, c} the set of Boolean action

variables. Agent 1 controls a, 2 controls b and 3 con-

trols c. Each Boolean variable can be set to true or

false by the agent controlling it. The goal of agent

1 is ϕ

= ¬a ∨ (a ∧ b ∧ ¬c). For agent 2 and 3 we

have ϕ

= a ↔ (b ↔ c) and ϕ

= (a ∧ ¬b ∧ ¬c) ∨

(¬a ∧ b ∧ c), respectively. We see that each goal is

a Boolean proposition and each agent aims to satisfy

its own goal, without knowledge of the other agents’

goals.

This game could, for instance, be understood as

three persons all being able to individually decide to

∗

This research was funded by a Research Foundation-

Flanders project.

go to a bar (set their variable to true) or to stay home

(set their variable to false), without knowing the in-

tentions of others. Given this intuition, the ﬁrst per-

son either wants to meet the second person without

the third or wants to stay home. The second person

either wants to meet both the ﬁrst and third person or

wants just one person to go to the bar. The third per-

son’s goal is either to only meet the second person or

to let the ﬁrst person be alone in the bar. So generally

in BGs, agents try to satisfy an individual goal, which

is formulated as a propositional combination of the

possible action variables of the agents. A neighbour

of an agent i is an agent whose goal depends on an

action controlled by agent i. In Example 1 all agents

are each other’s neighbours.

The strength of BGs lies in their compact repre-

sentation, since BGs do not require utility functions

to be explicitly mentioned for every strategy proﬁle.

Indeed, utility can be derived from the agents’ goals.

This advantage also has a downside: computing so-

lutions such as pure Nash equilibria (PNEs) is harder

than for most other game representations. Deciding

whether a PNE exists in a normal-form game is NP-

complete when the game is represented by the fol-

lowing items: (i) a set of players, (ii) a ﬁnite set of

actions per player, (iii) a function deﬁning for each

De Clercq S., Bauters K., Schockaert S., Mihaylov M., De Cock M. and Nowe A..

Decentralized Computation of Pareto Optimal Pure Nash Equilibria of Boolean Games with Privacy Concerns .

DOI: 10.5220/0004811700500059

In Proceedings of the 6th International Conference on Agents and Artiﬁcial Intelligence (ICAART-2014), pages 50-59

ISBN: 978-989-758-016-1

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

player which other players may inﬂuence their utility,

and (iv) the utility of each player, explicitly given for

all joint strageties of the player himself and the play-

ers inﬂuencing him (Gottlob et al., 2003). Deciding

whether a BG has a PNE, on the other hand, is Σ

complete

, even for 2-player zero-sum

games (Bon-

zon et al., 2006). This high complexity is undoubt-

edly part of the reason why, to the best of our knowl-

edge, there is no tailor-made method to compute the

PNEs of general BGs. However, some techniques are

described in the literature related to obtaining solu-

tions of BGs, e.g. ﬁnding PNEs for a certain class of

BGs or the use of bargaining protocols. These tech-

niques, and the differences from our approach, are

discussed in Section 5. Important to note is that, al-

though some of the existing approaches are also de-

centralized, none of them considers the issues of pri-

vacy and limited communication.

In this paper, we approach the problem of com-

puting a PNE of a BG, where we maintain privacy

of goals and reduce the amount of communication

among the agents. Agents could for instance be un-

willing or unable to share their goals, making a cen-

tralized approach unsuitable. Moreover, a central-

ized approach implies higher communication costs,

as agents exchange information with a central au-

thority. To cope with these concerns, we investigate

a decentralized algorithm, namely Win-Stay Lose-

probabilistic-Shift or WSLpS (Mihaylov, 2012). Our

solver is private in the sense that agents do not need to

communicate their goals, neither to a central author-

ity, nor to each other. To evaluate a goal, it is only

required to know what actions were chosen by all rel-

evant agents. Indeed, every agent communicates to

every relevant agent its own actions and whether its

goal is achieved, without specifying the goal.

The solution we obtain with WSLpS is Pareto op-

timal, a well-known and desirable property in game

theory. An outcome of a game is Pareto optimal if

no other outcome makes every player at least as well

off and at least one player strictly better off. Depend-

ing on the application, an additional advantage is that

WSLpS requires only the memory required to repre-

sent the current state. An agent does not remember

previous actions or outcomes, but only uses the last

outcome to choose new actions. As a comparison,

e.g. the Highest Cumulative Reward (HCR) (Shoham

and Tennenholtz, 1993) update rule in reinforcement

learning requires agents to remember the last l cho-

sen actions and outcomes. This advantage of WSLpS

This is also known as NP

-complete, a complexity

class at the 2

level of the Polynomial Hierarchy.

In zero-sum games, the utility of all players sums up to

0 for every outcome.

could play a crucial role in applications in which

agents have a limited memory, e.g. in wireless sensor

networks (Mihaylov et al., 2011).

The paper is structured as follows. First, some

backgroundon BGs and WSLpS is given in Section 2.

In Section 3 we describe how WSLpS can be used

to coordinate agents to a Pareto optimal PNE, i.e. to

teach agents how to set their action variables in or-

der to satisfy their goal. We prove that this algorithm

will converge to a Pareto optimal PNE iff there ex-

ists a global strategy for which all agents reach their

goal and the parameter choice satisﬁes an inequality.

In Section 4 we present the results of our experiments

and in Section 5 we discuss related work. Finally we

conclude the paper in Section 6.

2 PRELIMINAIRIES

In this section, we recall BGs and WSLpS, the algo-

rithm we will use to ﬁnd solution of BGs.

2.1 Boolean Games

The logical language associated with a set of atomic

propositional variables (atoms) V is denoted as L

and contains:

• every propositional variable of V,

• the logical constants ⊥ and ⊤, and

• the formulas ¬ϕ, ϕ → ψ, ϕ ↔ ψ, ϕ∧ψ and ϕ∨ ψ

for every ϕ, ψ ∈ L

An interpretation of V is deﬁned as a subset ξ of V,

with the convention that all atoms in ξ are set to true

(⊤) and all atoms in V \ξ are set to false (⊥). Such an

interpretation can be extended to L

in the usual way.

If a formula ϕ ∈ L

is true in an interpretation ξ, we

denote this as ξ |= ϕ. A formula ϕ ∈ L

is indepen-

dent from p ∈ V if there exists a logically equivalent

formula ψ in which p does not occur. The set of de-

pendent variables of ϕ, denoted as DV(ϕ), collects all

variables on which ϕ depends.

Deﬁnition 2.1 (Boolean Game (Bonzon et al., 2006)).

A Boolean game (BG) is a 4-tuple G = (N,V, π, Φ)

with N = {1,. . . , n} a set of agents, V a set of propo-

sitional variables, π : N → 2

a control assignment

function such that {π(1), . . ., π(n)} is a partition of

V, and Φ a collection {ϕ

, . .. , ϕ

} of formulas in L

The set V contains all action variables controlled by

agents. An agent can set the variables under its con-

trol to true or false. We adopt the notation π

for π(i),

i.e. the set of variables under agent i’s control (Bon-

zon et al., 2006). Every variable is controlled by ex-

actly one agent. The formula ϕ

is the goal of agent i.

DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns

For every p ∈ V we deﬁne π

−1

(p) = i iff p ∈ π

, so

−1

maps every variable to the agent controlling it.

Deﬁnition 2.2 (Relevant Agents, Neighbourhood and

Neighbours).

Let G = (N,V,π, Φ) be a BG. The set of relevant

variables for agent i is deﬁned as DV(ϕ

). The set

of relevant agents RA(i) for agent i is deﬁned as

∪

p∈DV(ϕ

)

−1

(p). The neighbourhood of agent i is

deﬁned as Neigh(i) = { j ∈ N : i ∈ RA( j)}. We say

that j is a neighbour of i iff j ∈ Neigh(i) \ {i}.

Example 2

Let G

be a 2-player BG with π

= {a

}, ϕ

= a

and

= a

∨ ¬a

. Then 1 is a relevant agent for 2, but

not for himself. The neighbourhoods in the game are

Neigh(1) = {2} and Neigh(2) = {1,2}.

Note that the relevant agents for agent i are all agents

controlling a variable on which agent i’s goal de-

pends (Bonzon et al., 2007). The neighbours of i are

all agents — excluding i — whose goal depends on a

variable under agent i’s control.

Deﬁnition 2.3 (Strategy Proﬁle).

Let G = (N,V, π, Φ) be a BG. For each agent i ∈ N

a strategy s

is an interpretation of π

. Every n-tuple

S = (s

, . .. , s

), with each s

a strategy of agent i, is a

strategy proﬁle of G.

Because π partitions V and s

⊆ π

, ∀i ∈ N, we

also use the set notation ∪

i=1

⊆ V for a strategy

proﬁle S = (s

, . .. , s

). With s

−i

we denote the

projection of the strategy proﬁle S = (s

, . .. , s

) on

N \ {i}, i.e. s

−i

= (s

, . .. , s

i−1

, s

i+1

, . .. , s

). If s

′

a strategy of agent i, then (s

−i

, s

′

) is a shorthand for

, . .. , s

i−1

, s

′

, s

i+1

, . .. , s

The utility function for every agent i follows di-

rectly from the satisfaction of its goal.

Deﬁnition 2.4 (Utility Function).

Let G = (N,V, π, Φ) be a BG and let S be a strategy

proﬁle of G. For every agent i ∈ N the utility function

is deﬁned as u

(S) = 1 iff S |= ϕ

and u

(S) = 0

otherwise.

A frequentlyused solution conceptin game theory

is the notion of pure Nash equilibrium.

Deﬁnition 2.5 (Pure Nash Equilibrium).

A strategy proﬁle S = (s

, . .. , s

) for a BG G is a pure

Nash equilibrium (PNE) iff for every agent i ∈ N, s

a best response to s

−i

, i.e. u

(S) ≥ u

−i

, s

′

), ∀s

′

⊆ π

In Table 1, the PNEs of the BGs of Example 1 and 2

are listed, using set notation.

The strategy proﬁle S = (

0, { c}) = {c} is thus the

unique PNE of G

. This means that if the third per-

son goes to the bar, no individual person can change

Table 1: The PNEs of the BGs G

and G

BG G

PNEs {c}

0, { a

}, { a

, a

}

his action to improve the outcome for himself. So

the third person cannot improve his own situation by

leaving. Similarly the ﬁrst and second person could

decide (individually) to come to the bar, but this indi-

vidual decision will not lead to a strictly better out-

come for them, since they already reach their goal

in S. Note that in Example 1 and 2, {c} respectively

, a

} are the unique Pareto optimal PNEs.

2.2 Win-Stay Lose-probabilistic-Shift

We now recall Win-Stay Lose-probabilistic-Shift

(WSLpS) (Mihaylov,2012),thealgorithmwe will use

to compute solutions in BGs. WSLpS resembles a

reinforcement learning algorithm, because it teaches

agents which actions are most beneﬁcial by reinforc-

ing the incentive to undertake a certain action which

has been successful in the past. The framework to

which it is applied consists of agents, which under-

take certain actions in pursuit of a goal. The agents

are connected with each other through neighbour re-

lations. Note that this concept of neighbours does not

necessarily correspond to Deﬁnition 2.2.

Using WSLpS, agents try to maximize a function

called success. There are multiple ways to choose this

function and the idea behind it is that, when every

agent has maximized its success function, all agents

must have reached their goal. In this paper we assume

that the function success, deﬁned for each agent and

each strategy proﬁle, only takes the values 0 and 1.

Given a certain strategy proﬁle S, each agent eval-

uates its success function. If its value is 0 (i.e. the

agent gets negative feedback), it shifts actions with

probability β. In case of positive feedback, it sticks to

its strategy choice. WSLpS was originally introduced

to solve normal-form coordination games. In those

games, all agents control similar actions and they all

try to select a comparable action. For example, if mul-

tiple people want to meet each other in a bar, but for-

get to mention which bar, they should all choose the

same bar in order to meet. One could then deﬁne an

agent i to be successful in iteration it iff every neigh-

bour of agent i has picked a similar action as i in the

current strategy proﬁle S

. Another option could be

that agent i is successful iff it picked a similar action

as a randomly selected neighbour. So in case of the

bar meeting example, an agent randomly thinks of a

friend and checks whether that friend is in the same

bar. If he is, the agent stays in that bar, if not, it goes

to a random bar with probability β.

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

Initially the agents randomly choose how to act.

The strategy proﬁle corresponding with this initial

choice is denoted as S

, with 0 the iteration num-

ber. WSLpS contains a parameter α ∈ ]0, 1], which

is used to compute the shift probability β in every it-

eration (see Section 3). The probability β depends on

the agent i and the strategy proﬁle S

that was chosen

in the current iteration it. The stochasitc algorithm

WSLpS has converged if, with probability 1, no agent

changes its actions anymore.

3 APPLYING WSLpS TO BGs

We can use WSLpS to create an iterative solver for

BGs as follows. In the ﬁrst iteration every agent ran-

domly sets each of the variables under its control to

true or false, without knowledge of the actions or

goals of the other agents. This can happen simultane-

ously for all agents. Subsequently every agent i eval-

uates the outcome. We assume that agents can check

whether their own goal is achieved. In some appli-

cations it is possible to evaluate a goal without com-

munication between agents, e.g. by observation of the

environment. If not, we allow agents to communicate

their actions to their neighbours. Further communica-

tion between agents is restricted to agents asking their

neighbours whether their goal is satisﬁed.

We use an additional parameter k, which deter-

mines the maximum number of neighbours we take

into account to evaluate the success function. With

this parameter we can control the amount of com-

munication between the agents. The range of k is

{1, 2, . . . , n}, and if |Neigh(i)| < k, we take i’s en-

tire neighbourhood into account. Therefore, we de-

ﬁne k

′

(i) as min(k, |Neigh(i)|). We denote the set of

all possible subsets of Neigh(i) with k

′

(i) elements

as SS(i, k). For every i ∈ N we deﬁne the discretely

uniformly distributed random variable RS(i, k), which

can take all values in SS(i, k). The binomial coefﬁ-

cient



|Neigh(i)|

′

(i)



is the cardinality of SS(i, k). So for

any set rs ∈ SS(i, k), the probability P(RS(i, k) = rs)



|Neigh(i)|

′

(i)



−1

For a BG G = (N,V, π, Φ) the function

success : 2

× 2

→ {0, 1} is deﬁned as

success(S, rs) = 1 iff u

(S) = 1, ∀ j ∈ rs and

success(S, rs) = 0 iff ∃ j ∈ rs : u

(S) = 0. For

every agent i ∈ N we deﬁne the random variable

success(S, RS(i, k)) which takes values in {0, 1}.

Speciﬁcally, success(S, RS(i,k)) = 1 with probability

∑

rs∈SS(i,k)

P(RS(i, k) = rs|success(S, rs) = 1). So the

random variable success(S, RS(i,k)) is 1 with prob-

ability 1 iff for any k

′

(i)-sized randomly selected

subset rs of Neigh(i) the goal of every agent in rs is

satisﬁed. If we observe the value rs ∈ SS(i, k) for

RS(i, k) in iteration it and success(S

, rs) = 1, this

positive feedback leads agent i to keep its current

strategy s

for the next iteration. If not, the negative

feedback drives the agent to independently ﬂip each

of the variables under its control with a probability of

β(S, i, rs) = max(α −

|{ j∈rs|u

(S)=1}|

′

(i)

, 0). Flipping a

variable means setting the corresponding variable to

true if it was false and vice versa. Note that RS(i, k)

takes a different value in every iteration, but the same

value is used by i within one iteration. So to compute

the shift probability, the agent uses the same random

subset as it did to evaluate its success function.

WSLpS has converged if, with probability 1, no

agent changes its actions anymore. To prove the con-

vergence of WSLpS, we use Markov chains. A ﬁnite

Markov chain (MC) is a random process that transi-

tions from one state to another, between a ﬁnite num-

ber of possible states, in which the next state depends

only on the current state and not on the sequence of

states that preceded it (Grinstead and Snell, 1997).

If the transition probabilities between states do not

alter over time, the MC is homogeneous. WSLpS,

applied to a BG, induces a homogeneous ﬁnite MC.

Lemma 3.1.

Let G = (N,V,π, Φ) be a BG. Suppose WSLpS is ap-

plied to G and the strategy proﬁle S was chosen in the

current iteration. For any strategy proﬁle S

′

, the prob-

ability of S

′

being chosen in the next iteration only

depends on S.

Proof. For all strategy proﬁles S and S

′

, deﬁne

v(S, S

′

, i) = ((S \ S

′

) ∪ (S

′

\ S)) ∩ π

. Intuitively

v(S, S

′

, i) is the set of variables under agent i’s con-

trol which are either true in S and false in S

′

or the

other way around. Let the function w : 2

× 2

× N

be deﬁned as w(S, S

′

, i) = 1 if v(S, S

′

, i) 6=

0 and 0 oth-

erwise. We will abbreviate the notations RS(i, k) and

SS(i, k) to resp. RS and SS. State S transitions to S

′

iff

every agent i ∈ N changes its strategy s

to s

′

. There-

fore it sufﬁces to prove that, for every i, the probabil-

ity of i changing s

to s

′

only depends on S. Take an

arbitrary i ∈ N. Then either v(S, S

′

, i) 6=

0, i.e. agent i

controls at least one variable that is ﬂipped during a

tranistion from S to S

′

, or v(S,S

′

, i) =

0, i.e. no vari-

ables controlled by i are ﬂipped during a transition

from S to S

′

. In the ﬁrst case, i can only change its

strategy from s

to s

′

if we observe a value rs ∈ SS

for RS such that success(S, rs) = 0. Moreover, i can

only change its strategy to s

′

if it ﬂips every variable

in v(S, S

′

, i), which happens independently with prob-

ability β(S,i, rs). For the other variables controlled

DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns

by i, i.e. π

\ v(S, S

′

, i), i can only change its strategy

to s

′

if it does not ﬂip any of those variables, which

happensindependently with probability 1−β(S, i, rs).

Since RS is a discrete random variable, the probability

of agent i transitioning from s

to s

′

∑

rs∈SS

(P(RS = rs)· (1− success(S, rs))

· β(S, i, rs)

|v(S,S

′

,i)|

· (1 − β(S,i, rs))

|π

\v(S,S

′

,i)|

In case v(S, S

′

, i) =

0, i can only change its strat-

egy from s

to s

′

if it does not ﬂips variables. This

can happen in two ways: either success(S, rs) = 0 but

all variables keep their current truth assignment, or

success(S, rs) = 1. So in this case the probability of

agent i transitioning from s

to s

′

∑

rs∈SS

(P(RS = rs) · ((1− success(S, rs))

· (1 − β(S,i, rs))

|π

+ success(S, rs))).

We can compute the probability of S transitioning to

′

∏

i∈N

((1− w(S, S

′

, i)) ·

∑

rs∈SS

(P(RS = rs) · β(S, i, rs)

|v(S,S

′

,i)|

· (1 − success(S, rs)) · (1− β(S,i, rs))

|π

\v(S,S

′

,i)|

)

+ w(S, S

′

, i) ·

∑

rs∈SS

(P(RS = rs) · ((1− success(S, rs))

· (1 − β(S,i, rs))

|π

+ success(S, rs)))). (1)

It holds that P(RS = rs) = |SS(i, k)|

−1

with

|SS(i, k)| =



|Neigh(i)|

′

(i)



. It is now clear that the transi-

tion probability only depends on S.

Deﬁnition 3.1.

Let G = (N,V, π, Φ) be a BG. Then the random pro-

cess with all strategy proﬁles of G as possible states

and with the probability of state S transitioning to

state S

′

given by (1) is called the random process in-

duced by WSLpS applied to G and denoted as M

The following property follows immediately from

Lemma 3.1 and Deﬁnition 3.1.

Proposition 3.2.

Let G = (N,V,π, Φ) be a BG. Then M

is a homoge-

nous MC and every iteration of WSLpS applied to G

corresponds to a transition of states in M

An absorbing state of a MC is a state which tran-

sitions in itself with probability 1. An absorbing MC

(AMC) satisﬁes two conditions: (i) the chain has

at least one absorbing state and (ii) for each non-

absorbing state there exists an accessible absorbing

state, where a state u is called accessible from a state v

if there exists a positive m ∈ N such that the proba-

bility of state v transitioning in state u in m steps is

strictly larger than 0. AMCs have an interesting prop-

erty (Grinstead and Snell, 1997): regardless of the in-

titial state, the MC will eventually end up in an ab-

sorbing state with probability 1. As such the theory

and terminology of MCs offer an alternative formu-

lation for convergence of WSLpS: WSLpS applied to

a BG G converges iff M

is an AMC.

Proposition 3.3.

Let G = (N,V, π, Φ) be a BG with non-trivial goals,

i.e. RA(i) 6=

0, ∀i ∈ N. With α >

k−1

, WSLpS applied

to G converges iff G has a strategy proﬁle S for which

every agent reaches its goal. Moreover, if WSLpS ap-

plied to G converges, it ends in a Pareto optimal PNE.

Proof. First note that S is an absorbing state of M

iff all agents get positive feedback for S with proba-

bility 1, i.e. success(S, rs) = 1, ∀rs ∈ ∪

i∈N

SS(i, k). We

claim this condition is equivalent with u

(S) = 1 for

all i. Since every agent must have at least one rele-

vant agent, success(S, rs) = 1 for all rs ∈ ∪

i∈N

SS(i, k)

directly implies u

(S) = 1 for every i. Conversely,

if u

(S) = 1 for all i, then all agents reach their

goal so in particular every neighbour of every agent

reaches its goal, implying success(S,rs) = 1 for all

rs ∈ ∪

i∈N

SS(i, k). So S is an absorbing state of M

iff

every agent reaches its goal in S. Consequently every

absorbing state S of M

is a Pareto optimal PNE.

WSLpS converges ⇒ ∃S, ∀i ∈ N : u

(S) = 1

This follows from the previous observation and the

fact that convergence of WSLpS applied to G corre-

sponds to M

ending up in an absorbing state.

WSLpS converges ⇐ ∃S, ∀i ∈ N : u

(S) = 1

Assume that there exists a strategy proﬁle S

, . . . , s

) of G with u

) = 1 for every agent i. We

already reasoned in the beginning of the proof that S

is an absorbing state of M

, so it is sufﬁcient to prove

that for each non-absorbingstate there exists an acces-

sible absorbing state. In that case M

is an AMC. Let

= (s

, . . . , s

) be an arbitrary non-absorbing state,

then ∃i

∈ N: u

) = 0. Consequently there exists

at least one agent which inﬂuences i

(i.e. RA(i

) 6=

and for every j ∈ RA(i

) there exists a rs ∈ SS( j, k)

with i

∈ rs. This implies that for every j ∈ RA(i

P(success(S

, j, RS(j,k)) = 0|S

, j) > 0.

There exists a strategy proﬁle S

such that s

, ∀ j ∈ RA(i

), and for all j ∈ N \ RA(i

) either

= s

or s

= s

. Moreover, the probability of

transitioning to S

is non-zero, due to the fol-

lowing reasons. First, we already reasoned that the

probability of all j ∈ RA(i

) getting negative feed-

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

back from S

is non-zero. Second, all agents with

positive feedback from S

stick with their current

strategy. Third, all agents with negative feedback

can change to any strategy with a non-zero proba-

bility; in particular, the probability that all agents

j, with negative feedback from S

, switch to s

non-zero. To see this, note that, given we observe

the value rs ∈ SS( j,k) for RS(j,k), the probabil-

ity of agent j ﬂipping a variable is β(S

, j, rs) =

max(α −

|{ j

′

∈rs|u

′

)=1}|

′

( j)

, 0). If agent j got nega-

tive feedback from S

, then success(S

, rs) = 0 and

there must be at least one neighbour j

′

of j with

′

) 6= 1. Considering the fact that α >

k−1

and

′

( j) = min(k, |Neigh( j)|), it follows that α >

′

( j)−1

′

( j)

Therefore it holds that β(S

, j, rs) is in ]0,1[ if agent

j got negative feedback from S

. So irrespective of

whether the transition from s

to s

requires ﬂipping

variables or not, the transition probability is non-zero.

Since u

) = 1 and s

= s

, ∀ j ∈ RA(i

), it follows

that u

) = 1. Either ∀i ∈ N: u

) = 1, so S

is an

accessible absorbing state, or ∃i

∈ N: u

) = 0.

As long as there exists an i

∈ N such that u

) = 0

we can ﬁnd a state S

l+1

= (s

l+1

, . . . , s

l+1

) such that

state S

can transition to S

l+1

with non-zero proba-

bility and such that s

l+1

= s

, ∀ j ∈ RA(i

), and for all

j ∈ N \RA(i

) either s

l+1

= s

or s

l+1

= s

. Moreover,

for every i

with 1 ≤ m ≤ l it holds that u

l+1

) = 1

because ∀ j ∈ RA(i

) : s

l+1

= s

. To see this, note that

we assumed that every j ∈ RA(i

) switched to s

the transition from S

to S

m+1

. In all the next transi-

tions, either j kept the previous strategy or switched

to s

, so in any case we have s

l+1

= s

. Clearly l = n

is the maximum value for which S

l+1

will be an ab-

sorbing state accessible from S

In the basic WSLpS algorithm, agents are altru-

istic: they take the satisfaction of their neighbours’

goals into account to reach a solution. Indeed, if the

success function of all relevant agents of i is maxi-

mized, then automatically agent i’s goal is satisﬁed.

We can also consider an alternative function

success(S, i) = u

(S), where agents are self-centered

and only check whether their own goal is satisﬁed.

However, using this success function, convergence

to a Pareto optimal PNE is no longer guaranteed.

Consider e.g the BG in Example 2. There is one

global solution {a

, a

}, but for initial states {a

} or

0 agent 2 has reached its goal and will never alter his

action. We can also combine self-centered and altru-

istic behaviour in the function success(S, i, rs) = 1 iff

(S) = 1 and u

(S) = 1 for every j in a random k

′

(i)-

sized subset rs of neighbours of i. It is easy to see

that Proposition 3.3 remains valid with this success

function.

4 EXPERIMENTS

In this section, we investigate the convergence of

WSLpS in a number of simulations

All measure-

ments have been performed on a 2.5 GHz Intel Core

i5 processor and 4GB of RAM. A BG generator was

implemented with 3 parameters: (i) the number of

agents, (ii) the number of variables controlled by one

agent, and (iii) the maximum number of operators ap-

pearing in a goal. We randomly generate goals with

∧, ∨ and ¬ and make sure there is a solution in which

every agent reaches its goal. To this end, we ﬁrst ran-

domly choose a strategy, and then repeatedly generate

clauses. If the clause is satisﬁed by the strategy it is

added as a goal to the problem instance; otherwise we

add its negation.

Experiment 1

In our ﬁrst experiment we generate one BG G with 30

agents, 10 action variables per agent and a maximum

of 15 operators in every goal. We ﬁx the parameter k

of WSLpS to 2 and run 1000 tests on G for various

values for α. Note that Proposition 3.3 only guaran-

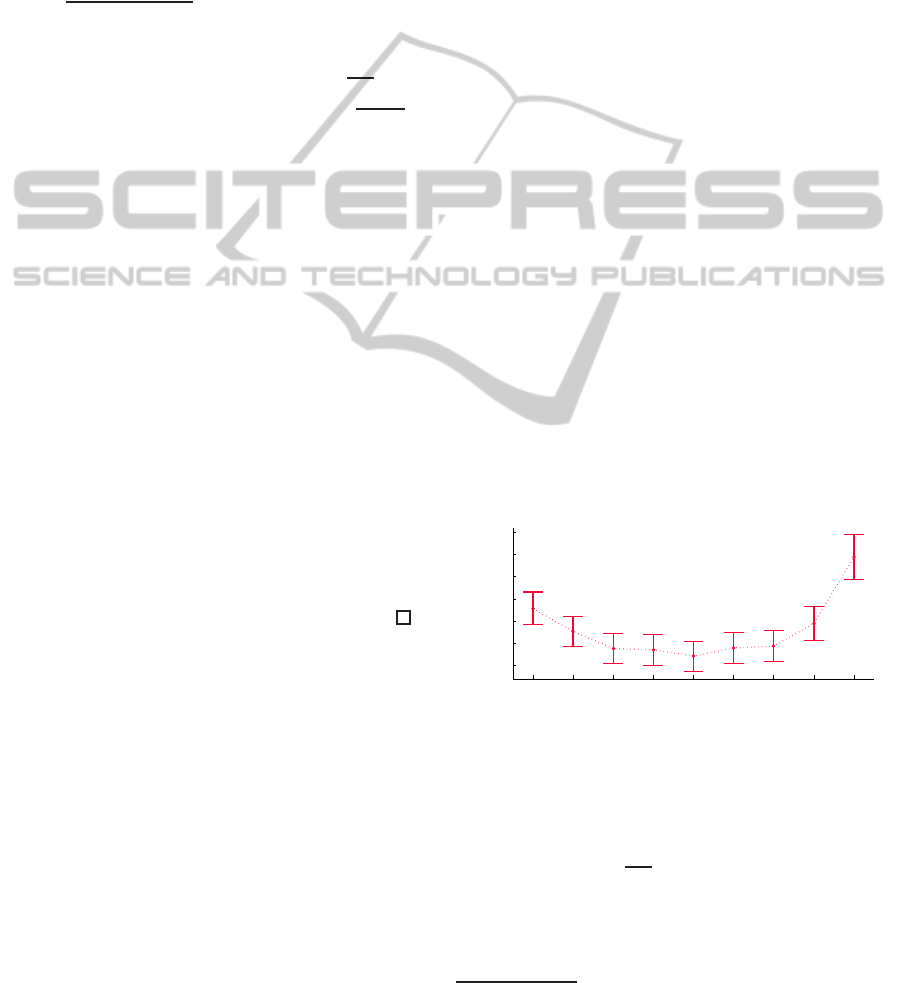
tees convergence for α > 0.5. Figure 1 shows the av-

erage number of iterations to convergence in function

of α, within a 95% conﬁdence interval of the mean.

Note that the X-axis does not have a linear scale.

0.505 0.51 0.52 0.53 0.54 0.55 0.56 0.6 0.7

2750

3000

3250

3500

3750

4000

4250

Parameter alpha

Average number of iterations

Figure 1: Iterations to convergence in function of α.

The best value for α lies close to the boundary for

convergence, namely 0.5. This observation has moti-

vated Experiment 3, where we will investigate more

closely how the optimal value for α relates to the the-

oretical boundary of

k−1

We see that α = 0.54 is the best tested value with

only 2851 (95% CI [2682, 3047]) iterations to conver-

gence on average, with an average computation time

of 62ms (95% CI [58, 66]). When we used the success

Implementations and data are available at http://

www.cwi.ugent.be/BooleanGamesSolver.html.

DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns

function mentioned at the end of Section 3 instead, i.e.

success(S, i) = 1 iff u

(S) = 1 and u

(S) = 1 for ev-

ery j in a random k

′

(i)-sized subset of i’s neighbours,

we observed that the convergence was much slower.

For α = 0.54, the average number of iterations to con-

vergence increased substantially to 22× 10

(95% CI

[21× 10

, 23× 10

]); note that this value is not shown

in Figure 1. This increase makes sense: agents start

changing their variables when their own goal is not

satisﬁed, even in case they do not inﬂuence their own

goal. Therefore these changes could drive the agents

away from a strategy that contributes to a global so-

lution. So our decentralized approach favors altruistic

agents. Hence, if agents cared about others, the whole

system will converge much faster, than if agents are

self-centered.

Experiment 2

For this experiment we look at the inﬂuence of the

ratio of the number of conjunctions to the number of

disjunctions per goal. To this end, we use a slightly

modiﬁed version of our generator, in which we ﬁrst

guess a strategy and then randomly generate clauses

with the requirednumberof conjunctionsand disjunc-

tions, keeping only those which are satisﬁed by the

strategy. For each tested ratio, we generate one BG

with 26 agents and 4 variables per agent. We ﬁx the

parameters to k = 2 and α = 0.54 and run 1000 tests

for all ratios. For the ratio 6/0 we do no reach conver-

gence within 10

iterations. Figure 2 shows the aver-

age number of iterations to convergence, in a 95% CI

of the mean, scaled logarithmically.

0/6 1/5 2/4 3/3 4/2 5/1

Number of conjunctions/disjunctions per goal

Average number of iterations

Figure 2: Iterations to convergence for ratios of conjunc-

tions/disjunctions.

If the goals only contain disjunctions, the average

number of iterations to convergence is 3 (95% CI

[2, 4]), with an average computation time of 2.1ms

(95% CI [2.0, 2.2]). As the number of conjunctions

increases compared to the number of disjunctions, the

average number of iterations to convergence also in-

creases. These results are intuitive: the more conjunc-

tions in the goals, the fewer absorbing states, so the

slower the convergence of WSLpS. Disjunctions have

the exact opposite effect. Note, however, that the po-

sitions of the operators in the goals and the (number

of different) action variables occuring in the goals can

also inﬂuence the number of absorbing states.

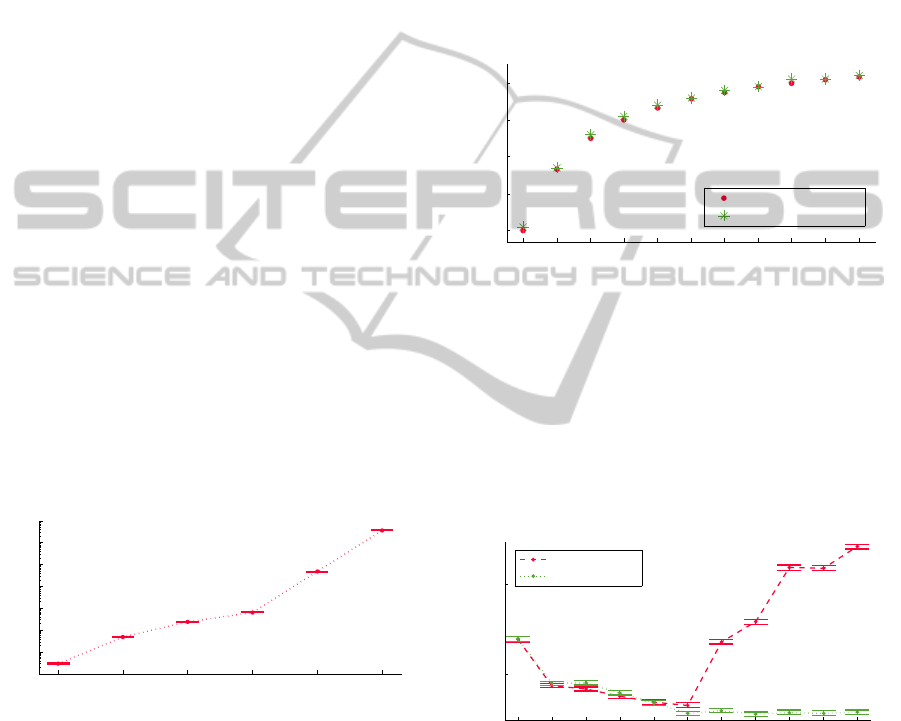
Experiment 3

In this experimentwe investigate the effect of parame-

ter k on the choice of parameter α. We have generated

one random BG G with 45 agents, 6 action variables

per agent and at most 14 operators occuring in every

goal. The maximum size of a neighbourhood in G

is 12. For each k we determine the best value for α by

empirical analysis, up to 2 digits accuracy, the result

of which is shown in Figure 3.

2 3 4 5 6 7 8 9 10 11 12

0.5

0.6

0.7

0.8

0.9

Parameter k

Parameter alpha

theoretical boundary

best alpha

Figure 3: Best α in function of k.

We see that the best value for α always lies surpris-

ingly close to the boundary value for convergence we

derived in Proposition 3.3. In Figure 4 we plot the

average number of iterations to convergence, within

a 95% CI based on 1000 tests, for different values

of k. For each k we ﬁx α with the values of Figure 3.

The average number of iterations to convergence are

scaled logarithmically.

2 3 4 5 6 7 8 9 10 11 12

Parameter k

Average number of iterations

fixed alpha

computed alpha

Figure 4: Iterations to convergence in function of k.

In Figure 4 we notice something peculiar when the

value of α is ﬁxed in this way: as we increase the

value of k, the average number of iterations to con-

vergence explodes. This is counterintuitive because

the higher k is, the more information the agents use

to evaluate their success function and choose new ac-

tions. However, some agents may have fewer than k

neighbours, i.e. k

′

(i) 6= k. For those agents another α

would be more suitable, but the basic WSLpS algo-

rithm uses the same α for all agents. To analyze

ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence

this effect, we use an alternative implementation of

WSLpS, in which every individual agent i computes

its own α as

100

ﬂoor(100·

′

(i)−1

′

(i)

) + 0.01. Using this

new implementation, we repeat our experiments for

different values of k. The results are also plotted in

Figure 4. This time we get more intuitive results:

WSLpS converges faster when more neighbours are

asked whether their goal is satisﬁed. Note however

that a higher k implies higher communication costs.

One can thus trade off communication costs for con-

vergence speed.

5 RELATED WORK

In this section we discuss related work and explain

how it differs from ours. One aspect in which it can

differ is the studied solution concept. Indeed, there

exist many solution concepts of BGs besides PNEs,

e.g. the (weak and strong) core (Dunne et al., 2008;

Bonzon et al., 2012), veriﬁable equilibria (

Agotnes

et al., 2013) and stable sets (Dunne et al., 2008), al-

though this latter term is also used to describe certain

coalitions (Bonzonet al., 2007). In this paper we have

restricted the discussion to PNEs, since it is one of

the most common, intuitive and straightforward solu-

tion concepts in gametheory (Daskalakiset al., 2006).

Note that not all BGs necessarily have a PNE, but

our method is restricted to BGs with a strategy proﬁle

such that every agent reaches its goal, which automat-

ically implies the existence of a PNE. Indeed, a strat-

egy proﬁle satisfying all agents’ goals is by deﬁnition

a PNE.

In (Dunne et al., 2008), a bargaining protocol for

BGs is introduced. Agents negotiate in rounds by

successively proposing an outcome which the oth-

ers can accept or reject. Under the quite severe re-

striction that the goals of the agents are positive (i.e.

only ∧ and ∨ may be used), the negotiations end dur-

ing the ﬁrst round and any strategy proﬁle resulting

from the negotiations is Pareto optimal if the agents

follow speciﬁc negotiation strategies. If the restric-

tion is not met, the negotiations can last n rounds —

with n the number of agents — and obtaining a so-

lution is not guaranteed. Like WSLpS, this bargain-

ing protocol is decentralized. It has, however, some

privacy concerns: in contrast to WSLpS, it assumes

that agents know each other’s goals because they try

to make a proposal which is at least as good as the

previous one for all agents which still need to make

a proposal. With an example we illustrate that, even

when the assumption of positive goals and knowledge

of each other’s goals is met, the bargaining protocol

might not be a feasible method. Consider for instance

the situation where agents have to decide which road

to pick to go from point A to point B. Assuming that

all roads are equally suitable, it might be a realistic

assumption that all agents know each other’s goals,

since all agents will probably want to balance the load

on the roads. But clearly it is not realistic that hun-

dreds or thousands of agents will negotiate to decide

who will take which road. In this kind of situations,

involving a large number of agents, WSLpS can nar-

row the communication down to a feasible level, by

choosing a small k. Interestingly, the class of BGs

for which the bargaining protocol is guaranteed to ob-

tain a solution is a subclass of the class of BGs for

which WSLpS is guaranteed to converge to a solu-

tion. Indeed, if the goals of the agents are positive,

then clearly every agent reaches its goal in the strat-

egy proﬁle S = V. Therefore, the restriction on BGs

formulated in Proposition 3.3 is met. Moreover, the

class of BGs in which agents’ goals are positive is

a strict subset of the class of BGs for which a strategy

proﬁle exists such that every agent reaches its goal,

since e.g. the BG in Example 2 does not belong to the

ﬁrst class, but does belong to the second class.

In (Bonzon et al., 2007), a centralized algorithm

is provided to compute PNEs of BGs for which the ir-

reﬂexive part of the dependency graph is acyclic. The

dependency graph of a BG connects every agent with

its relevant agents. A BG for which the irreﬂexive

part of the dependency graph is acyclic has at least

one PNE (Bonzon et al., 2007). Moreover, the au-

thors show that PNEs of BGs can also be found by

computing the PNEs of subgames of the BG. More

speciﬁcally, a BG is decomposed using a collection

of stable sets which covers the total set of agents.

It is shown that if there exists a collection of PNEs

of the subgames — with exactly one PNE for ev-

ery subgame — such that the strategies of agents be-

longing to multiple stable sets of the covering agree,

then the strategy proﬁle obtained by combining these

strategies is a PNE of the original BG. It is, how-

ever, important to note that a decomposition based on

stable sets cannot remove or break cycles in the de-

pendency graph. Indeed, the decomposition is only

used to speed up the computation of the PNEs by di-

viding the problem in smaller problems (divide-and-

conquer). Therefore, the usage of the centralized al-

gorithm combined with the decomposition is still re-

stricted to BGs for which the irreﬂexive part of the

dependency graph is acyclic. It is easy to verify that

there are BGs which meet the restriction of this algo-

rithm but do notmeet the condition of Proposition 3.3.

An example of such a BG is the 2-player BG with

= {a

}, ϕ

= a

and ϕ

= ¬a

∧ ¬a

. Similarly,

there exist BGs which do have a strategy proﬁle such

DecentralizedComputationofParetoOptimalPureNashEquilibriaofBooleanGameswithPrivacyConcerns

that every agent reachesits goal, but cannot be tackled

by the algorithm in (Bonzon et al., 2007). To see this,

consider e.g. the 2-player BG deﬁned by π

= {a

= a

↔ a

and ϕ

= a

↔ ¬a

. Note however that

is makes less sense to combine both approaches into

a hybrid algorithm to tackle a wider space of BGs. In-

deed, centralized and decentralized approaches both

have their speciﬁc application areas. In some appli-

cations, agents are unable to communicate with each

other, e.g. due to high communication costs or the

lack of common communication channels, and there

might not be a central entity either, making a cen-

tralized approach unsuitable. Consider for instance

the earlier mentioned load balancing problem. Even

though it would be in their advantage, it is question-

able whether e.g. human car drivers would let a cen-

tral authority dictate which road to take to drive to

work. Moreover, some agents’ goals might be to

take a speciﬁc road, for some private reason. It is

unlikely that humans would be willing to share this

information with a central authority. Therefore, the

private goal assumption, made by WSLpS, could be

very valuable in some application areas. Due to the

decentralized nature of WSLpS, agents do not need

to share any private information and therefore, un-

like most centralized algorithms, our approach is said

to respect the privacy of agents. In other contexts,

e.g. where the agents are truck drivers on a private

domain, owned and instructed by a company, a cen-

tralized approach might be suitable. Note however

that the BG corresponding to the load balancing prob-

lem does not satisfy the condition that its dependency

graph is acyclic, since every agent depends on every

other agent.

In (Wooldridge et al., 2013), taxation schemes

are investigated for BGs with cost functions. These

BGs impose costs on the agents, depending on which

actions they undertake (Dunne et al., 2008). Via

the agents’ utility, these costs allow for a more ﬁne-

graned distinction between strategy proﬁles. A tax-

ation scheme in (Wooldridge et al., 2013) consists

of an external agent, called the principal, which im-

poses additional costs to incentivise the agents to ra-

tionally choose an outcome that satisﬁes some propo-

sitional formula Γ. For example, one can deﬁne a

taxation scheme such that the resulting BG has at

least one PNE and all PNEs satisfy Γ. In contrast

to WSLpS, this approach is centralized: a central en-

tity uses global information to ﬁnd a taxation scheme.

Moreover, these taxation schemes are not developed

with the aim of computing solutions of the original

BG, but they are used to send the agents in certain

desirable directions. The scheme alters the original

solutions such that the agents are coordinated to new,