Overlapping Clustering with Outliers Detection

Amira Rezgui

, Chiheb-Eddine ben N’Cir

and Nadia Essoussi

LARODEC, ISG Tunis, University of Tunis, Bardo, Tunis, Tunisia

LARODEC, FSEG Nabeul, University of Carthage, Nabeul, Tunisia

Keywords:

Overlapping Clustering, Non Disjoint Groups, Parametrized R-OKM, Outliers Detection.

Abstract:

Detecting overlapping groups is an important challenge in clustering offering relevant solutions for many

applications domains. Recently, Parametrized R-OKM method was deﬁned as an extension of OKM to control

overlapping boundaries between clusters. However, the performance of both, OKM and Parametrized R-OKM

is considerably reduced when data contain outliers. The presence of outliers affects the resulting clusters and

yields to clusters which do not ﬁt the true structure of data. In order to improve the existing methods, we

propose a robust method able to detect relevant overlapping clusters with outliers identiﬁcation. Experiments

performed on artiﬁcial and real multi-labeled data sets showed the effectiveness of the proposed method to

produce relevant non disjoint groups.

1 INTRODUCTION

Data mining aims at modeling relationships and dis-

covering hidden patterns in large databases. Clus-

tering is an important task in data mining. It aims

to ﬁnd groups from unlabeled data by organizing a

given set of data into coherent clusters, such that

all data within the same cluster are similar to each

other, while data from different clusters are dissimi-

lar. However, this deﬁnition of clustering could be a

crucial issue in many applications of clustering where

data need to be assigned to more than one cluster. For

example, in social network analysis, community ex-

traction algorithms should be able to detect overlap-

ping clusters because an actor can belong to multiple

communities (Wang et al., 2010). In video classiﬁ-

cation, overlapping clustering is a necessary require-

ment while video can potentially have multiple genres

(Yang et al., 2007). In emotion detection, overlapping

clustering methods should be able to detect several

emotions for a speciﬁc piece of music (Trohidis et al.,

2008). In biology, many genes are multi-functional

and need to be assigned to multiple overlapping clus-

ters (Battle et al., 2005) (Eran et al., 2003). In infor-

mation retrieval and text mining, documents can dis-

cuss several themes (Sahami et al., 1996).

The possibility that an observation belongs to

more than one cluster is usually ignored. How-

ever, some researchers have focused on this prob-

lem known as ”overlapping clustering”. Recently, a

new clustering method referred to as Parametrized R-

OKM (Ben N’Cir et al., 2013), generalizes k-means

approach to detect non disjoint clusters. This method

extends OKM (Cleuziou, 2008) to control the sizes of

overlaps and offers for users the possibility to regu-

larize the overlaps. Although the ability of OKM and

Parametrized R-OKM to produce non-disjoint clus-

ters, their performance could be considerably reduced

in presence of outliers. Known that these methods are

based on centroids as representatives of each cluster,

the noisy observations lead to produce clusters which

do not ﬁt the true structure of data.

In order to deal with this issue, we propose a

robust method referred to Robust Parametrized R-

OKM, taking into account the presence of outliers.

When performing the learning of data, the proposed

method identiﬁes on each step observations which

will be classiﬁed as outliers to improve the quality of

obtained non-disjoint groups.

The remainder of this paper is organized as fol-

lows: Section 2 presents related works on overlapping

clustering. Then, Section 3 describes the motivation

of this work by presenting the importance of detect-

ing outliers. Section 4 describes the proposed Ro-

bust Parametrized R-OKM while Section 5 describes

experiments performed on artiﬁcial and real overlap-

ping data sets to check the effectiveness of the pro-

posed method. Finally Section 6 gives conclusions

and some future improvements of this work.

279

Rezgui A., Ben N’Cir C. and Essoussi N..

Overlapping Clustering with Outliers Detection.

DOI: 10.5220/0004830002790286

In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 279-286

ISBN: 978-989-758-018-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 OVERLAPPING CLUSTERING

Many methods were proposed to solve the issue

of overlapping clustering. Two classes of methods

have been led: Heuristic and Theoretical. Heuristic

methods are based on proposing new clustering

processes based on intuitive learning for example

CBC (Pantel and Dekang, 2002), POBOC (Cleuziou

et al., 2004) or the extension of results of well

known methods (Bezdek, 1981) (Krishnapuram and

Keller, 1993) (Dempster et al., 1977) to have non

disjoint clusters. These heuristic methods can lead

to non disjoint partitioning, but good results are not

ensured because they are not based on theoretical

model to introduce overlaps. However, this issue

is solved for theoretical methods where overlaps

are introduced in their optimized criteria. Example

of these Methods are OKM (Cleuziou, 2008) and

Parametrized R-OKM (Ben N’Cir et al., 2013).

• Parametrized R-OKM

In order to detect overlapping clusters with control of

overlaps, Parametrized R-OKM method generalizes

OKM and allows the user to parameterize the size of

the overlaps according to his expectations. Given a

data set X with N data and a number K of expected

clusters, the aim of Parametrized R-OKM is to ﬁnd

the binary assignment matrix Π(N × K) and the clus-

ter representativesC = {C

,...,C

} such that the fol-

lowing objective criterion is minimized:

J(Π,C) =

∑

∈X

|Π

d(x

,im

Π,C

))

, (1)

with im

Π,C

) is the combination of clusters’ repre-

sentatives which represents the gravity center of clus-

ters prototypes to which observation x

belongs and is

deﬁned by:

Π,C

) =

∑

∈Π

|Π

, (2)

where π

the set of objects which belongs to the

cluster, C

the prototype of cluster π

, |Π

the

weight assigned to observation x

, Π

the set of clus-

ters to which x

belongs to, |Π

| its cardinality and

α a positive parameter to control the size of the over-

laps. The parameter α is considered as a penalty term:

the penalization is more important when α → +∞ and

then overlaps are reduced. However the penalization

is reduced when α → 0 and the method produces large

overlaps. Particularly when α = 0 Parametrized R-

OKM coincides with OKM.

The objective function of Parametrized R-OKM

J(Π,C) is minimized by alternating two independent

steps:

1. Assignment of observationsto one or several clus-

ters: This step orders the clusters from the nearest

cluster to farthest one then assigns the observation

to several clusters while the objective function is

minimized.

2. Update of clusters’ representatives: This step up-

date the clusters’ representatives after each as-

signment step. By using the lagrange multipliers

method, by differentiating with respect to C

and

setting derivative to zero, optimal clusters’ rep-

resentatives C

∗

to made the objective function of

Parametrized R-OK minimized are deﬁned by:

∗

∑

∈π

|Π

2−α

∑

∈π

|Π

2−α

, (3)

where C

= |Π

|.x

− (|Π

| − 1).im

Π,C(x

)

3 PROBLEM DESCRIPTION

In real life applications of overlapping clustering, data

are usually complex and contain outliers. Outliers,

also referred to as noise, are observations which are

grossly different from the remaining set of data. In-

tuitively, an outlier can be deﬁned by an observation

that deviates so much from other observations.

The presence of outliers in data affects the clus-

tering algorithm by biasing the structure of obtained

clusters as the case of Parametrized R-OKM. Figure

1 shows patterns obtained with parametrized R-OKM

in two artiﬁcial data sets: the ﬁrst example is free of

outliers while the second contains a noisy observa-

tion. The application of Parametrized R-OKM with 2

clusters using Euclidean distance in the ﬁrst data set

leads to non disjoint clusters. However, in the sec-

ond data set the application of Parametrized R-OKM

results in two disjoint groups where the outlier itself

forms one cluster and all remaining observations are

grouped in the other cluster..

4 ROBUST PARAMETRIZED

R-OKM

In order to make robust the identiﬁcation of over-

lapping clusters in presence of outliers, we propose

a new method denoted by Robust Parametrized

R-OKM. This proposed method takes into account

that data may contain noise. Therefore, it can detect

more relevant clusters by giving the possibility to

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

280

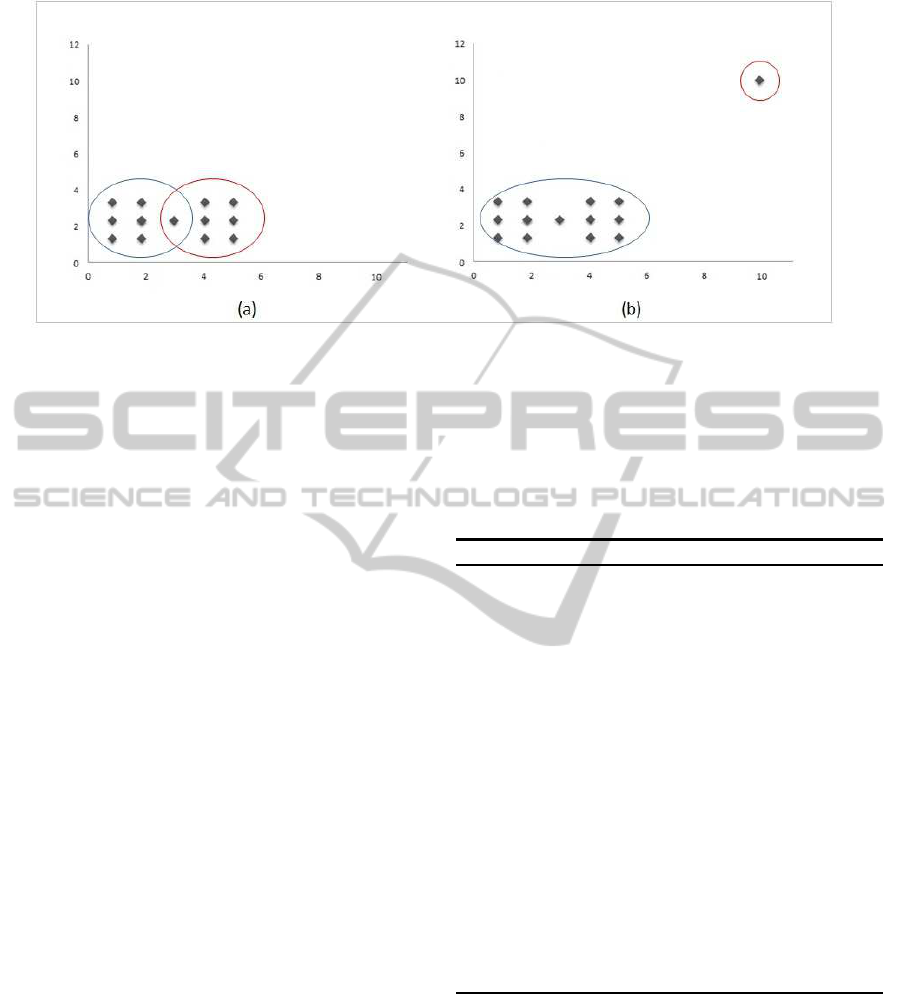
Figure 1: Clusters obtained using Parametrized R-OKM ( K=2) in a two dimensional artiﬁcial data sets: (a) tow non disjoint

clusters obtained in a data set free of outliers and (b) two disjoint clusters obtained in a data set containing a noisy observation.

user to control the size of overlaps: Based on the

Noise Clustering approach (Dav`e, 1991), we propose

to add a new ﬁctive cluster in which outliers will be

assigned to. All the observations whose distances

from the set of prototypes exceed a ﬁxed threshold

are considered as outliers and assigned to the ﬁctive

cluster.

4.1 Objective Function of Robust

Parametrized R-OKM

The Objective function of Robust Parametrized R-

OKM aims to model the local error on each obser-

vation x

deﬁned by the squared Euclidean distance

between x

and its representative denoted as image

im(x). Given a data set X with N data over R

and

a number K

′

= K + 1 of expected clusters, the aim of

Robust Parametrized R-OKM is to ﬁnd the binary as-

signment matrix Π(N × K

′

) and the cluster represen-

tatives C = {C

,. ..,C

} ∪C

‡

such that the following

objective function is minimized:

J(Π,C,δ) =

∑

∈X,x

/∈C

‡

|Π

d(x

,im

Π,C

))

∑

∈C

‡

|Π

, (4)

where |Π

the weight of observation x

, |Π

| the

number of clusters to which x

belongs to, α a pos-

itive parameter used to control the size of overlaps,

Π,C

) the image of observation x

, C

‡

the noise

cluster and δ

the distance between the cluster noise

and each observation denoted by noise distance.

4.2 Algorithm Resolution and

Optimization

The main algorithm of the Robust Parametrized R-

OKM is described by Algorithm 1.

Algorithm 1: Robust Parametrized R-OKM.

Require: X :a set of input data.

K : a number of clusters.

ε : a minimum improvement in the objective function.

max

:a maximum number of iterations.

: the distance noise

Ensure: Π: assignment of observations over K clusters.

1: Initialize representatives of clusters C

randomly over X

2: Initialize the distance noise δ

3: Initialize clusters memberships Π

using

Robust.Multi.ASSIGN(x

)

4: Compute the objective function J(J(Π

,δ) ).

5: while J



t−1

,δ



− J(Π

,δ) > ε and t < t

max

6: Set t = t + 1

7: Update clusters’ representatives C

8: Update distance noise δ

9: Compute new assignments Π

using

Robust.Multi.ASSIGN(x

,Π

)

10: Compute objective function J(Π

,δ)

11: end while

12: return Π

the ﬁnal cluster memberships matrix.

The optimization of the objective function is realized

by iterating 3 steps:

1. computation of cluster representatives ;

2. computation of distance noise δ

;

3. multi-assignment (Π) of observations.

The above steps are iterated until a stopping criterion

is reached. The stopping rule of Robust Parametrized

R-OKM algorithm is characterized by two criteria:

the maximum number of iterations or the minimum

OverlappingClusteringwithOutliersDetection

281

improvement of the objective function between two

iterations.

We present in the next, a detailed description

of the optimisation steps of Robust Parametrized R-

OKM.

4.3 Computation of Cluster

Representatives

Given a cluster π

and a set of K clusters’ represen-

tatives {C

}

h=1

\ {C

} the problem of ﬁnding C

∗

that

minimize the objective function J(Π,C, γ) can be ex-

pressed as a convex optimization problem which is

solved using the lagrange multipliers method. By dif-

ferentiating J(Π,C, γ) with respect to C

and setting

derivative to zero, optimal clusters’ representative C

∗

which minimize the objective function are computed

as the following:

∗

∑

∈π

,π

6=C

‡

|Π

2−α

∑

∈π

|Π

2−α

, (5)

where C

is deﬁned by :

= |Π

|.x

− (|Π

| − 1).im

Π,C(x

)

(6)

The computation of the new clusters’ prototypes en-

sures that the objective function is decreased after

each update of clusters’ prototypes.

4.4 Multi-assignment

Based on the assignment heuristic used for

Parametrized R-OKM, we derive a new heuris-

tic taking into account the possibility that an

observation be assigned to the noise cluster. It

looks for the nearest cluster of observation x

. If the

distance between this observation and the nearest

cluster exceeds the distance noise, this observation

is identiﬁed as outlier. Conversely, it scrolls through

the list of centers from the nearest to the farthest,

and assigns the observation x

to the nearest cluster.

The new assignment is kept only if it is better than

the old one. This assignment heuristic is detailed in

Algorithm 2.

4.5 Computation of Distance Noise

In order to determine the noise distance, we assume

that this distance depend on the variation of obser-

vations with respect to clusters prototypes which is

deﬁned by:

Algorithm 2: Robust.Multi.ASSIGN.

Require: x

:Vector in R

,. ..,C

} : K clusters’ representatives.

old

: Old assignment of observation x

γ : Parameter to control outliers.

Ensure: Π

: New assignment for x

1: Search C

∗

the nearest cluster where C

∗

argmin

∑

k∈Π

|Π

−C

2: Compute the distance between the observation and the

nearest cluster

3: if |Π

−C

∗

≥ δ

then

4: x

is an outlier Π

= {C

‡

}

5: Return Π

6: else

7: Initialize Π

= {C

∗

} the nearest cluster where C

∗

argmin

|Π

−C

8: Looking for the next nearest cluster C

∗

which is not in-

cluded in Π

9: Compute im

′

) with assignments Π

′

= Π

∪ {C

∗

}

10: if |Π

′

− im

′

< |Π

− im

Π,C

then

11: Π

← Π

′

and go to step 9

12: else

13: compute im

old

(xi) with assignment Π

old

14: if |Π

− im

Π,C

≤ |Π

old

− im

Π,C

then

15: Return Π

16: else

17: Return Π

old

18: end if

19: end if

20: end if

= γ

∑

i=1

∑

k=1

N × K

, (7)

where γ is the value of the parameter used to obtain δ

from the average of distances. A proper selection of

the parameter γ will control the classiﬁcation result

and the proportion of observations that are considered

as outliers. The speciﬁcation of the parameter γ is

ﬁxed by the user.

According to this deﬁnition, the noise distance

depends generally on the non-weighted distances

of all feature vectors to all prototype vectors. Thus

this distance is not ﬁxed but it is modiﬁed in each

iteration of the algorithm after the update of clusters’

representatives.

5 EXPERIMENTS AND RESULTS

To check the effectiveness of Robust Parametrized R-

OKM to produce suitable overlapping clusters within

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

282

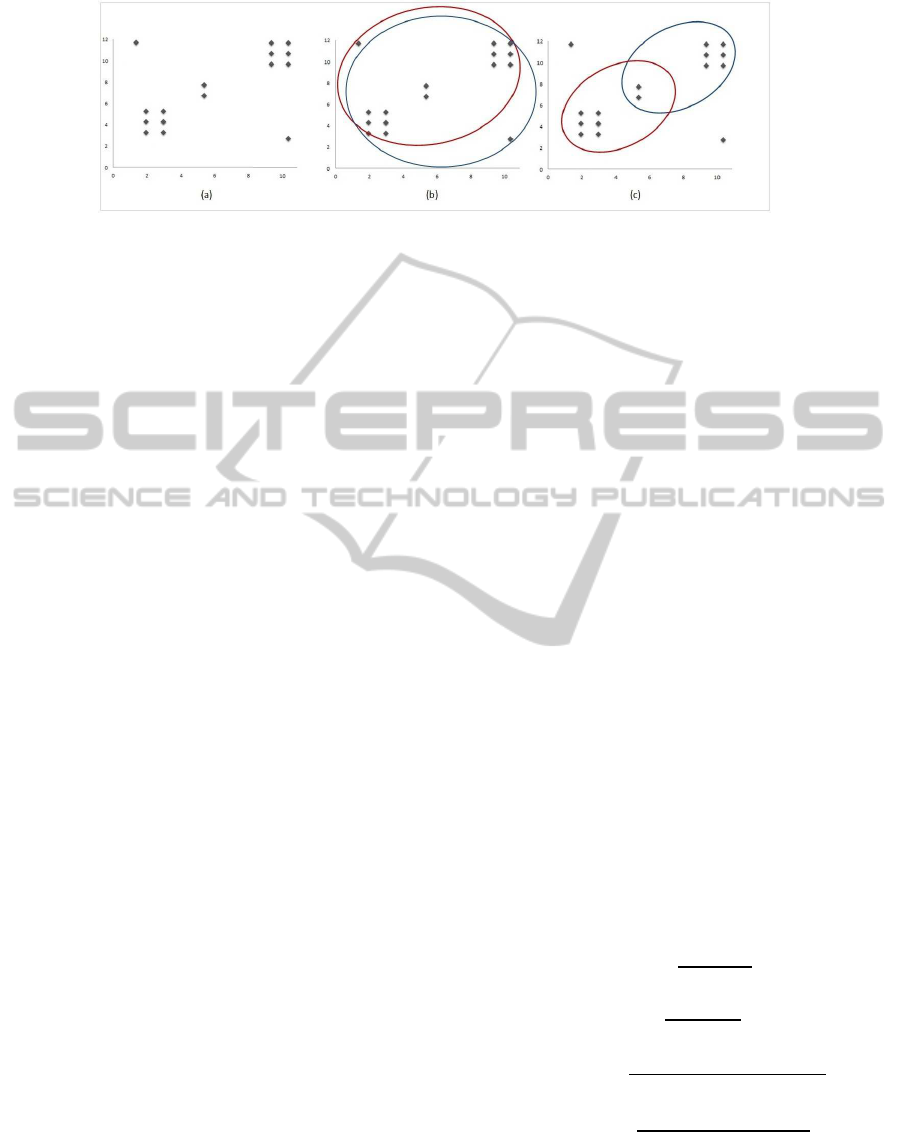
Figure 2: Experiments on artiﬁcial data set: (a) the artiﬁcial data set, (b)two clusters obtained using Parametrized R-OKM

with α = 1 and (c)two clusters obtained using Robut Parametrized R-OKM with α = 1 and γ = 0.5.

noisy data, we perform experiments on artiﬁcial and

real overlapping data sets using a standard desktop

computer. Running times of each method are not re-

ported while all the methods need less than one 1 sec-

ond to return results.

5.1 Experiments on Artiﬁcial Data Sets

The examples included in Figure 2(b) and Figure

2(c) show the ability of Robust Parametrized R-OKM

method lead to clusters which ﬁt the true structures in

data.

To check the effectiveness of Robust Parametrized

R-OKM, , we generate an artiﬁcial data set over two

dimensions as described in Figure 2(a). This data set

is characterized by two apparent groups in data and

some observations which have different characteris-

tics than the remaining data. We report obtained par-

titioning using Parametrized R-OKM with α = 1 and

Robut Parametrized R-OKM with α = 1 and γ = 0.5

as described in Figure 2(b) and Figure 2(c). These

ﬁgures show that Parametrized R-OKM leads to clus-

ters with large overlaps and does not identify the two

apparent groups. This problem is solved when using

the proposed Robust Parametrized R-OKM.

To illustrate sensitivity of Robust Parametrized R-

OKM to the parameter γ, we report obtained clusters

with different values of γ using a ﬁxed value of α as

shwon in Figure 3. These results provethat the perfor-

mance of Robust Parametrized R-OKM depends on a

suitable conﬁguration of the parameter γ. This corre-

lation can be explained by the fact that the parame-

ter γ is used to control the number of outlier points.

In fact, the parameter γ controls the distance between

each observation and the prototype of cluster in which

the outliers are assigned to. This distance depends on

this parameter. As well as γ is small and near to 0 the

distance noise becomes more smaller leading to large

detection of outliers.

5.2 Experiments on Real Data Set

In order to evaluate the performance of Robust

Parametrized R-OKM, results are compared through

external validation measures which are Precision, Re-

call, F-measure and Rand Index. The reported scores

are averages and standard deviations obtained over

ten runs.

Let X = {X

,. ..,X

} be the set of observations, C =

,. ..,c

} a partition of X into K classes, R =

,..., r

} a partition of X into K

clusters speciﬁed

by the clustering algorithm.

Given the notations:

• ”TP” designs the number of pairs of observations

in X that share at least one class in C and share at

least one cluster in R.

• ”TN” the number of pairs of observations in X

that do not share any class in C and do not share

any cluster in R;

• ”FN” designs the number of pairs of observations

in X that share at least one class in C and do not

share any cluster in R;

• ”FP” designs the number of pairs of observations

in X that do not share any class in C and share at

least one cluster in R

the validation measures are computed as follows:

Precision =

TP+ FP

Recall =

TP+ FN

F − measure =

(2× Recall× Precision)

(Recall + Precision)

Rand Index =

TP+ TN

TP+ FN + FP+ TN

Experiments are performed in three domains where

data need to be assigned to more than one cluster. The

statistic of the used data sets are described in Table 1.

OverlappingClusteringwithOutliersDetection

283

Figure 3: Sensitivity of Robust Parametrized R-OKM method to the parameter γ.

Table 2: Comparison of Robust Parametrized R-OKM with existing overlapping clustering methods on Benchmark data sets.

Data sets Methods Precision Recall F-measure Rand Index

EachMovie fuzzy c-means (θ = 0.33) 0.610 ± 0.001 0.734 ± 0.001 0.666 ± 0.001 0.696 ± 0.001

OKM 0.465± 0.020 0.921±0.055 0.618± 0.001 0.532± 0.032

Robust Parametrized R-OKM(γ = 0.8) 0.627± 0.010 0.857± 0.020 0.724 ± 0.02 0.621± 0.03

Parametrized R-OKM(α = 0.1) 0.474± 0.016 0.900± 0.042 0.621± 0.024 0.547± 0.024

Robust Parametrized R-OKM(γ = 1.0) 0.680± 0.024 0.727± 0.084 0.699± 0.024 0.640 ± 0.025

Emotion fuzzy c-means (θ= 0.1667) 0.493 ± 0.003 0.357 ± 0.001 0.414 ± 0.002 0.524 ± 0.002

OKM (α = 0) 0.483± 0.000 0.647± 0.029 0.553± 0.011 0.508± 0.001

Robust Parametrized R-OKM(γ = 10) 0.657±0.004 0.512± 0.017 0.578 ±0.012 0.517± 0.003

Parametrized R-OKM(α = 5.0) 0.506± 0.002 0.213± 0.007 0.300± 0.008 0.531 ± 0.000

Robust Parametrized R-OKM(γ = 0.1) 0.698± 0.000 0.222± 0.021 0.337± 0.024 0.440± 0.004

Scene FCM(θ = 0.1667) 0.324± 0.004 0.482± 0.022 0.388± 0.005 0.706± 0.008

OKM 0.233± 0.006 0.928± 0.013 0.372± 0.008 0.397± 0.019

Parametrized R-OKM(α = 2.0) 0.451± 0.000 0.417± 0.001 0.433± 0.001 0.789 ± 0.000

Robust Parametrized R-OKM(γ = 0.8) 0.488± 0.030 0.652± 0.119 0.548± 0.023 0.632± 0.019

Table 1: Data sets description.

Data set Observation Dimension Labels Overlap

EachMovie 75 3 3 1.14

Music 593 72 6 1.86

Scene 2407 6 1.07 1.86

Table 2 and Table 3 report average scores and standard

deviations of Precision, recall, F-measure.

In Eachmovie, Emotion and Scene data sets, re-

sults obtained with Robust Parametrized R-OKM out-

perform results obtained with FCM and Parametrized

R-OKM. For example, in Eachmovie data set the

F-measure obtained with Robust Parametrized R-

OKM (0.724) outperform the F-measure obtained

with OKM (0.618) and the F-measure obtained with

FCM(0.666). The improvement of F-measure with

proposed methods is induced by the improvement of

classiﬁcation precision compared to OKM and FCM

methods.

In Emotion and Scene data set, the improvement

of the F-measure obtained with the proposed method

compared to the F-measure obtained with Robust

Parametrized R-OKM is induced by the improvement

of classiﬁcation precision. For example, in Emo-

tion data set, the average of Precision using Robust

Parametrized R-OKM with α = 5 and γ = 0.1 is equal

to 0.506 while the average of Precision when using

Parametrized R-OKM with α = 5 is equal to 0.698.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

284

Table 3: Sensitivity of proposed methods to the parameter γ on Benchmark data sets.

Data sets Methods Precision Recall F-measure Rand Index

EachMovie Robust Parametrized-OKM(α = 0,γ = 1) 0.632± 0.02 0.886± 0.05 0.737±0.03 0.635± 0.04

Robust Parametrized-OKM(α = 0,γ = 0.8) 0.627± 0.01 0.857± 0.02 0.724± 0.02 0.621± 0.03

Robust Parametrized-OKM(α = 0,γ = 0.7) 0.623± 0.01 0.868± 0.04 0.725± 0.01 0.619± 0.02

Robust Parametrized R-OKM(α = 1,γ = 1) 0.691± 0.05 0.635± 0.03 0.659±0.03 0.619± 0.05

Robust Parametrized R-OKM(α = 1,γ = 0.7) 0.691±0.06 0.621± 0.06 0.652± 0.04 0.611± 0.06

Robust Parametrized R-OKM(α = 1,γ = 0.5) 0.661± 0.03 0.605± 0.07 0.631± 0.05 0.583± 0.04

Robust Parametrized R-OKM(α = 1.5,γ = 1) 0.719±0.10 0.632± 0.05 0.668±0.05 0.631± 0.06

Robust Parametrized R-OKM(α = 1.5,γ = 0.7) 0.711± 0.09 0.611± 0.05 0.653± 0.01 0.617± 0.18

Robust Parametrized R-OKM(α = 1.5,γ = 0.5) 0.663± 0.03 0.603± 0.07 0.630± 0.05 0.583± 0.04

Emotion Robust Parametrized-OKM(α = 0,γ = 0.3) 0.659± 0.005 0.519± 0.038 0.580± 0.022 0.521± 0.007

Robust Parametrized-OKM(α = 0,γ = 0.4) 0.657± 0.005 0.491± 0.013 0.562± 0.006 0.510± 0.000

Robust Parametrized-OKM(α = 0,γ = 0.8) 0.654± 0.003 0.492± 0.039 0.561± 0.024 0.507± 0.009

Robust Parametrized-OKM(α = 0,γ = 5.0) 0.661± 0.006 0.487± 0.02 0.560± 0.011 0.510± 0.002

Robust Parametrized R-OKM(α = 5,γ = 0,1) 0.698± 0.000 0.222± 0.021 0.337± 0.024 0.440± 0.004

Robust Parametrized R-OKM(α = 5,γ = 0,5) 0.677± 0.00 0.203± 0.00 0.313± 0.00 0.428± 0.000

Robust Parametrized R-OKM(α = 5,γ = 0.7) 0.679± 0.002 0.207± 0.00 0.318± 0.00 0.429± 0.00

Robust Parametrized R-OKM(α = 5,γ = 1.0) 0.672± 0.000 0.200± 0.004 0.308± 0.004 0.424± 0.001

Robust Parametrized R-OKM(α = 0.1,γ = 0,1) 0.700± 0.002 0.285± 0.006 0.405± 0.006 0.462± 0.003

Robust Parametrized R-OKM(α = 0.1,γ = 0.3) 0.681± 0.001 0.244± 0.015 0.388± 0.011 0.454± 0.004

Robust Parametrized R-OKM(α = 0.1,γ = 0.5) 0.676± 0.002 0.262± 0.034 0.377± 0.036 0.447± 0.011

Robust Parametrized R-OKM(α = 0.1,γ = 1.0) 0.676± 0.001 0.256± 0.037 0.370± 0.039 0.445± 0.013

Scene Robust Parametrized-OKM(α = 2.0,γ = 0.2) 0.514± 0.055 0.960± 0.000 0.672± 0.040 0.509± 0.051

Robust Parametrized-OKM(α = 2.0,γ = 0.5) 0.480± 0.050 0.557± 0.048 0.511± 0.009 0.578± 0.025

Robust Parametrized-OKM(α = 2.0,γ = 0.8) 0.488± 0.030 0.652± 0.119 0.548± 0.023 0.632± 0.019

Robust Parametrized-OKM(α = 2.0,γ = 5.0) 0.514± 0.000 0.682± 0.005 0.586± 0.001 0.688± 0.000

Robust Parametrized R-OKM(α = 0.8,γ = 0.2) 0.514± 0.053 0.960± 0.000 0.668± 0.045 0.509± 0.051

Robust Parametrized R-OKM(α = 0.8,γ = 0.5) 0.492± 0.041 0.585± 0.064 0.529± 0.002 0.593± 0.013

Robust Parametrized R-OKM(α = 0.8,γ = 1.0) 0.471± 0.020 0.672± 0.110 0.548± 0.023 0.631± 0.018

Robust Parametrized R-OKM(α = 0.8,γ = 5.0) 0.514± 0.000 0.726± 0.039 0.586± 0.002 0.688± 0.000

Robust Parametrized R-OKM(α = 0.4,γ = 0.2) 0.514± 0.053 0.960± 0.000 0.668± 0.045 0.509± 0.051

Robust Parametrized R-OKM(α = 0.4,γ = 0.8) 0.473± 0.018 0.639± 0.135 0.536± 0.038 0.623± 0.009

Robust Parametrized R-OKM(α = 0.4,γ = 1.0) 0.525± 0.002 0.672± 0.003 0.590± 0.003 0.686± 0.000

Robust Parametrized R-OKM(α = 0.4,γ = 5.0) 0.516± 0.002 0.684± 0.008 0.588± 0.004 0.689± 0.001

Table 3 evaluates the sensitivity of proposed

method to the parameter γ respectively on Emotion,

EachMovie and Scene data sets. Using EachMovie

and Scene data sets, F-measure and Rand Index de-

crease when γ decrease. However F-measure and

Rand Index decrease when γ increase using Emotion

data set.

6 CONCLUSIONS

Overlapping clustering is a necessary requirement for

many applications of clustering where data need to

be assigned to more than one cluster. Existing over-

lapping clustering methods can produce non disjoint

clusters, but its is not well adapted for clustering noisy

data. The performance of these methods are reduced

when data contain noisy observations. The proposed

method, Robust Parametrized R-OKM solves this is-

sue and identiﬁes more relevant clusters which ﬁt the

true structures in data. Experiments performed in arti-

ﬁcial and real data sets showed the robustness of pro-

posed method when data contain noise.

As future work, we plan to conﬁrm preliminary

obtained results on other real overlapping data sets.

Instead, one could add an auto adjusted value of γ to

automatically control the outliers boundaries in real

life applications of overlapping clustering.

REFERENCES

Battle, A., Segal, E., and Koller, D. (2005). Probabilis-

tic discovery of overlapping cellular processes and

their regulation. Journal of computational biology

: a journal of computational molecular cell biology,

12(7):909–927.

Ben N’Cir, C., Cleuziou, G., and Essoussi, N. (2013). Iden-

tiﬁcation of non-disjoint clusters with small and pa-

rameterizable overlaps. In Computer Applications

Technology (ICCAT), 2013 International Conference

on, pages 1–6.

Bezdek, J. C. (1981). Pattern recognition with fuzzy objec-

tive function algoritms. Plenum Press, 4(2):67–76.

OverlappingClusteringwithOutliersDetection

285

Cleuziou, G. (2008). An extended version of the k-means

method for overlapping clustering. In International

Conference on Pattern Recognition ICPR, pages 1–4,

Florida, USA. IEEE.

Cleuziou, G., Martin, L., Vrain, C., and Vrain, C. (2004).

Poboc: an overlapping clustering algorithm. applica-

tion to rule-based classiﬁcation and textual data. In

Proceedings of the 16th European Conference on Ar-

tiﬁcial Intelligence (ECAI-04), pages 440–444.

Dav`e, R. N. (1991). Characterization and detection of

noise in clustering. Pattern Recognition Letters,

12(11):657–664.

Dempster, A. P., Laird, N. M., and Rubin, D. B. (1977).

Maximum likelihood from incomplete data via the em

algorithm. Journal of the royal statistical society, se-

ries B, 39(1):1–38.

Eran, S., Alexis, B., and Daphne, K. (2003). Decompos-

ing gene expression into cellular processes. In Paciﬁc

Symposium on Biocomputing’03, pages 89–100.

Krishnapuram, R. and Keller, J. M. (1993). A possibilistic

approach to clustering. Trans. Fuz Sys., 1(2):98–110.

Pantel, P. and Dekang, L. (2002). Discovering word senses

from text. In Proceedings of ACM SIGKDD Con-

ference on Knowledge Discovery and Data Mining,

pages 613–619.

Sahami, M., Hearst, M. A., and Saund, E. (1996). Apply-

ing the multiple cause mixture model to text catego-

rization. In Saitta, L., editor, Machine Learning, Pro-

ceedings of the Thirteenth International Conference

(ICML ’96), pages 435–443.

Trohidis, K., Tsoumakas, G., Kalliris, G., and Vlahavas,

I. P. (2008). Multi-label classiﬁcation of music into

emotions. In Bello, J. P., Chew, E., and Turnbull, D.,

editors, ISMIR, pages 325–330.

Wang, X., Tang, L., Gao, H., and Liu, H. (2010). Discov-

ering overlapping groups in social media. In Proceed-

ings of the 2010 IEEE International Conference on

Data Mining, ICDM ’10, pages 569–578, Washing-

ton, DC, USA. IEEE Computer Society.

Yang, J., Yan, R., and Hauptmann, A. G. (2007). Cross-

domain video concept detection using adaptive svms.

In Proceedings of the 15th international conference

on Multimedia, MULTIMEDIA ’07, pages 188–197,

New York, NY, USA.

ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods

286