Semantic Labelling of 3D Point Clouds using Spatial Object Constraints

Malgorzata Goldhoorn

and Ronny Hartanto

University of Bremen, Robotics Research Group, Bremen, Germany

DFKI GmbH, Robotics Innovation Center, Robert-Hooke-Straße 5, 28359 Bremen, Germany

Keywords:

Point Clouds, Probabilistic Methods, Scene Understanding, Object Recognition, Semantic Labelling, 3D

Scene Interpretation, Feature Extraction.

Abstract:

The capability of dealing with knowledge from the real human environment is required for autonomous sys-

tems to perform complex tasks. The robot must be able to extract the objects from the sensors’ data and give

them a meaningful semantic description. In this paper a novel method for semantic labelling is presented. The

method is based on the idea of connecting spatial information about the objects to their spatial relations to

other entities. In this approach, probabilistic methods are used to deal with incomplete knowledge, caused by

noisy sensors and occlusions. The process is divided into two stages. First, the spatial attributes of the objects

are extracted and used for the object pre-classiﬁcation. Second, the spatial constraints are taken into account

for the semantic labelling process. Finally, we show that the use of spatial object constraints improves the

recognition results.

1 INTRODUCTION

For some time, there has been increasing interest to

develop autonomous systems, which can support the

human in everyday tasks. The robot should help peo-

ple by, for example, preparing breakfast or cleaning

the room. This is, of course, a futuristic scenario, be-

cause the areas of robotics and AI are very challeng-

ing and there are many problems that must be solved,

until this becomes a reality. One of the so far unsolved

problems is understanding the real human environ-

ment. To do a task planning, the robot must know the

meaning of the objects in a given task and at the same

time deal with missing information, resulting through

occlusion and partly caused by noisy sensors. In this

paper we describe a method which may be used for

such a purpose. The main contribution is the presen-

tation of a new idea which combines the spatial in-

formation about the object with constraints between

objects using probabilistic methods.

This paper presents our approach for semantic la-

belling of 3D point clouds, in which the transition

from the spatial into the semantic domain is done.

The remainder of this paper is organized as follows.

Section 2 gives an overview of the state of the art in

this ﬁeld. Section 3 introduces the method for point

cloud segmentation. Section 4 describes the ﬁrst step

of the approach, namely the probabilistic object pre-

classiﬁcation. Section 5 presents the idea of the object

constraints. Section 6 gives a quantitative survey of

our algorithm. Finally, conclusions and opportunities

for future work are given.

2 RELATED WORK

For some time, semantic perception became one of

the most investigated research areas in robotics. This

is not least because of the increasing amount of low

cost 3D sensors like the Microsoft Kinect, but also

the fact that semantic perception is a capability which

autonomous systems need to be equipped with to per-

form complex tasks (Galindo et al., 2008), (Pangercic

et al., 2010). One of the recent works in this ﬁeld was

presented in (Anand et al., 2012). The authors pro-

posed a method for semantic labelling and search in

indoor scenes using a geometrical context. In their

approach, merged point clouds taken with a Kinect

sensor are used. They try to extract geometric prim-

itives from the data. To obtain a better view of the

scene, an active object recognition is used. G

unther

et al. (G

unther et al., 2011) present another related

work about semantic object recognition from 3D laser

data. In this work, a CAD-based method for object

classiﬁcation was proposed. For this, the geometrical

basic primitives of the objects are extracted and com-

513

Goldhoorn M. and Hartanto R..

Semantic Labelling of 3D Point Clouds using Spatial Object Constraints.

DOI: 10.5220/0004874205130518

In Proceedings of the 9th International Conference on Computer Graphics Theory and Applications (WARV-2014), pages 513-518

ISBN: 978-989-758-002-4

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

pared if they ﬁt a given, known CAD model. N

uchter

et al. (N

uchter and Hertzberg, 2008) introduce a 6D

SLAM approach with semantic object recognition. In

this approach, the objects (like walls, doors, and ceil-

ings) are recognised from composed point clouds. To

classify other objects like robots or humans, trained

classiﬁers are used. Another approach for semantic

labelling was proposed in (Rusu et al., 2009). The au-

thors of this work use model-based object recognition

and try to recognise household objects in a kitchen en-

vironment, like furnitures and stoves. To infer about

these objects, the furniture features like knobs and

buttons are extracted beforehand. In (Aydemir et al.,

2010), semantic knowledge is used to search for spe-

ciﬁc objects. The authors try to ﬁnd a potential place

in which the object could be found using a reason-

ing module. The authors in (Galindo et al., 2008) and

(Galindo et al., 2005) describe the use of semantic

maps for task planning and spatial reasoning. They

use marker identiﬁcation to perform semantic inter-

pretation of entities and to bridge the gap between the

semantic and spatial domains.

3 APPEARANCE BASED

OBJECTS

PRE-IDENTIFICATION

In human living environments and especially in the

domestic one, many regularities with regards to the

objects’ occurrences can be found. For example,

some objects like furniture have deﬁned heights and

are larger than some other objects. Other objects like

ﬂat screen or keyboard have approximately the same

width but they have different depth. In general, the

objects could be distinguished from each other based

on their different spatial features. We make use of

those premises to do the object pre-classiﬁcation step.

The next very important point is that most of the ob-

jects in the domestic environment are approximately

planar surfaces. Therefore we try to segment these

planes and extract the spatial features from them. We

call this step “pre-classiﬁcation”, because in this stage

of our algorithm the objects are classiﬁed only by

their spatial features, without taking into account their

spatial relations to each other. As a result of this

step we obtain a probability distribution about object

classes given the measured values.

3.1 Point Cloud Pre-processing

The object recognition approach starts with the seg-

mentation of planes from the raw 3D point cloud data.

The data is taken with a tilting LIDAR (Light Detec-

tion and Ranging) laser system. For the segmenta-

tion, an optimised region growing algorithm is used.

This algorithm based on the approach in (Vaskevicius

et al., 2007) and was already mentioned in (Eich et al.,

2010). We extended this algorithm to deal with an un-

organized point clouds, like in the case of data from

our tilting system. In such point cloud data, the points

are not available in memory as a grid and their near-

est neighbours cannot be accessed directly. Because

of that, the complexity of the algorithm increases by

the nearest neighbours search. Therefore, we made

some optimisation steps, which make the algorithm

much faster then the original one (Vaskevicius et al.,

2007). We do not describe the algorithm in detail,

because it was already mentioned in our other work

(Eich et al., 2010). The algorithm segments the in-

put 3D point cloud into planes, which can be used for

the future processing step. The region growing needs

as an input different starting parameters, whose val-

ues determine the result of the segmentation. These

parameters are: the maximum distance between two

points, the maximum distance between a point and

plane, the maximum mean squared error of the plane,

the minimum number of points, which a plane needs

to have, and the maximum number of nearest neigh-

bours of a single point. The algorithm ends when all

points have been examined and results in a set of ex-

tracted planes. Fig. 1 shows the result of the segmen-

tation after applying the listed parameters.

3.2 Extraction of Spatial Object

Attributes

The extraction of spatial features of the objects starts

once the planes are segmented. In this step the spatial

features of each plane, like the size of a plane A ∈ R,

the rectangularity of the plane R ∈ [0, 1], its length and

width E ∈ R

, its orientation O ∈ H, and its center of

mass P ∈ R

are extracted and stored in a so called

feature vector Φ = (A, E, R, O, P). For better identi-

ﬁcation of these features, the found regions are ﬁrst

projected into 2D space. This is done by applying

the reverse rotation for pitch and yaw to the original

translated plane. In the end, the normal vector of the

plane is parallel to the global z-axis. We assume that

through our region growing algorithm this object ap-

proximates a planar surface. Since we already rotated

and translated the surface into the xy-plane we can

simply set all remaining z-values to zero. By doing

this we project the approximately planar surface to a

planar surface. Afterwords the calculations of their

hulls take place. For this, an alpha shape method from

the computational geometry algorithm library CGAL

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

514

Figure 1: Result of the region growing segmentation algorithm. The left image shows the given input raw data taken in one

of our ofﬁces and the right one presents the result of the segmentation, the randomly coloured planes.

is used. Having the 2D hull of a plane enables easier

extraction of the geometrical features. Figure 2 shows

the extracted plane together with its hull.

These ﬁve features are required to distinguish be-

tween different classes of objects. The most relevant

features are orientation and position. Using these at-

tributes it can be decided e.g. if a given object is rather

a ﬂat screen or a keyboard. On the other hand, the

position can be used to distinguish between objects

like walls, ﬂoors, and ceilings. The other features like

size, maximum expansion and rectangularity of the

plane increase the assignment of the object to a given

object class. At this point, it is important to mention

that the feature rectangularity is not a very critical fea-

ture for the classiﬁcation and it is hard to deﬁne, and

describe how rectangular an object is. Nevertheless, it

improves the detection of appropriate objects. In the

following, a short description of the features and their

processing are given. For the extraction of the max-

imum expansion of the plane we use a method from

the well-known OpenCV library. This function cal-

culates a minimum bounding box of the plane from

its hull. This bounding box has attributes like width,

height, and orientation. We take the width and height

of the box and treat them as the width and height of

the plane. The size of a segmented plane is calculated

using the even-odd algorithm. To do this, a set of 2D-

vectors are created to form the hull by using CGAL

functions. From these vectors a ﬁlled bitmap of each

object is created using this algorithm. We choose a

standard size of 640x480 to represent the converted

bitmap objects. The scaling factor is created by using

the information we already gathered from the max-

imum expansion which was explained before. The

rectangularity of the plane can be computed by di-

viding the area of the plane by the area of its bound-

ing box. Here, an assumption must be made that a

perfectly rectangular plane has the same area as its

bounding box. This is, hence, a critical point since

occlusion of objects could inﬂuence the recognition.

The resulting value is the percentage correspondence

of area sizes, while the percentage squareness accord-

ing to the deﬁnition mentioned above. The calculation

could here be done straight forward since through the

size computation of the created bitmap a normaliza-

tion took already place. We count only the ﬁlled pixel

and divide them by the total pixel count of our vir-

tual bitmap. The orientation of the plan is calculated

using the GNU Scientiﬁc Library. The mass cen-

troid axes are determined by eigenvectors and their

eigenvalue. We deﬁne that the eigenvector with the

smallest eigenvalue corresponds to the z-axis of the

plane and denotes its normal vector. The eigenvector

with the intermediate eigenvalue denotes the shorter

axis, namely the x-axis. The last eigenvector with the

biggest eigenvalue coincides with the y-axis of the

plane. By assuming that the z-vector has the small-

est eigenvalue, the objects were nearly “ﬂat” on their

(local) x-/y- plane. This assumption helps us with all

post-processing steps, because we can now handle ob-

jects completely invariant from their orientation. The

position of the plane results from the center of gravity

of all points of the plane.

3.3 Evaluation based on Objects

Appearance

After extracting the spatial features of the plane, the

evaluation step is done. To correctly evaluate the vec-

tor, a priori knowledge of the objects in the environ-

ment must be taken into account. This knowledge in-

dicates how the objects in a typical human environ-

ment look like and what their spatial values are. If we

take a table as an example then we know that it stays

on the ﬂoor, is very often rectangular and its height is

about 0.8 meters. Such an assumptions can be made

for all objects in the human environment. Exactly this

knowledge is stored in a database and serves as an

input for the evaluation function, with the aid of the

features are evaluated. In the database, objects like

table, wall, ﬂoor, ceiling, keyboard, ﬂat screen, and

“unknown object” are stored. Each spatial value of

an object contains an expected value µ and standard

deviation σ. These two values enable to having ob-

jects which different appearance and helps with their

robust pre-classiﬁcation. Because of the difference in

SemanticLabellingof3DPointCloudsusingSpatialObjectConstraints

515

Figure 2: Result of the alpha shapes calculation together with the associated regions, segmented in the previous step.

the importance of the given attributes, a weight is ap-

plied to each of them. The features are evaluated by

using the well known Bayes’ theorem. First, we cal-

culate the Gaussian distribution function, which gives

the probability of the measured value x to the known

object class C from the database. After some calcula-

tions and reformulations we obtain the formula 1:

P(C|Φ) =

∑

i=1

P(C|x

) · F

∑

i=1

(1)

This results in a probability distribution for a given

object class C from the data base given the measured

feature vector Φ.

4 SEMANTIC LABELLING WITH

SPATIAL CONSTRAINTS

The last step in our semantic labelling algorithm is

the classiﬁcation of the objects based on their spatial

relations. In the previous processing step, each seg-

mented plane was assigned to each object class from

the database with given probability. This objects as-

signment to a given class is based exclusively on the

spatial attributes of the object. Because of noise and

occlusion in the data, this can in many cases result

in an incorrect classiﬁcation of the object. In order

to improve the labelling we take spatial relations be-

tween all object classes into account. For this we de-

ﬁne a constraint network similar to (N

uchter et al.,

2003), in which the objects and their spatial relations

are stored. We use relations like “parallel” , “orthog-

onal”, “above”, “under”, or “equal height”. We treat

these relations as constraints that must be satisﬁed for

an object to belong to a given object class. In this

ﬁnal step of our algorithm, the valid world model is

tried to be found. To do this, the resulting objects of

the pre-classiﬁcation are sorted by their height. This

enables ﬁnding a ground plane (e.g. ﬂoor), which

is necessary to build the scene right up to the ceil-

ing, iteratively. The condition is, that the object is

pre-classiﬁed as a ﬂoor with a probability of at least

40%. Further, the next objects from the sorted list

are taken. During this, it is checked if the constraints

related to the relations between objects are satisﬁed.

If not, the current path will be discarded and a sim-

ple backtracking takes place. For our heuristic we

use the probability of associated object classes that

we calculated for each plane in our previous step (see

Sec. 3.1). By using this heuristic, in the case that

the pre-calculation was already correct, the right path

would be taken directly without any search. If dur-

ing traversing the path, an invalid model is found, it is

discarded automatically and the next best path is cho-

sen. This is done, because we assume that an error in

the world-model is (mostly) related to wrong hierar-

chies of objects. An example could be when an object

that is possibly a ﬂat screen is not located on top of a

desk. This whole search/backtracking is repeated un-

til the ceiling is found. The result of the algorithm is

a list of labelled objects together with their adjusted

probability. In this way the objects get clear semantic

descriptions.

5 EXPERIMENTS AND RESULTS

We have done several experiments using both raw

point cloud and synthetic data to evaluate our algo-

rithm. The raw data was taken in several ofﬁces of

our lab. This data has been recorded using a Hokuyo

UTM-30LX laser scanner mounted on a tilting unit.

The synthetic data has been generated using Blender

with some artiﬁcial noises. At the beginning, the pre-

classiﬁcation step of our algorithm was tested. For

this we took the real and synthetic data and tried

to ﬁgure out how good the extracted spatial features

matches the ground truth data to evaluate the overall

measurement accuracy. For this the large set of per-

fect generated sensor data were used. The result of

the test is that besides some rounding problems (po-

tentially caused by the ﬂoating point precision) the

measured values correspond to the ground truth data.

Further, we evaluate the inﬂuence of the each changed

feature on the probability result. As expected, the

changes in the value of the features has no large im-

pact on the result of the pre-classiﬁcation. This is be-

cause it is not relevant if a table is farther right or left,

only the height of the objects has a large importance

for their recognition. An example evaluation can bee

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

516

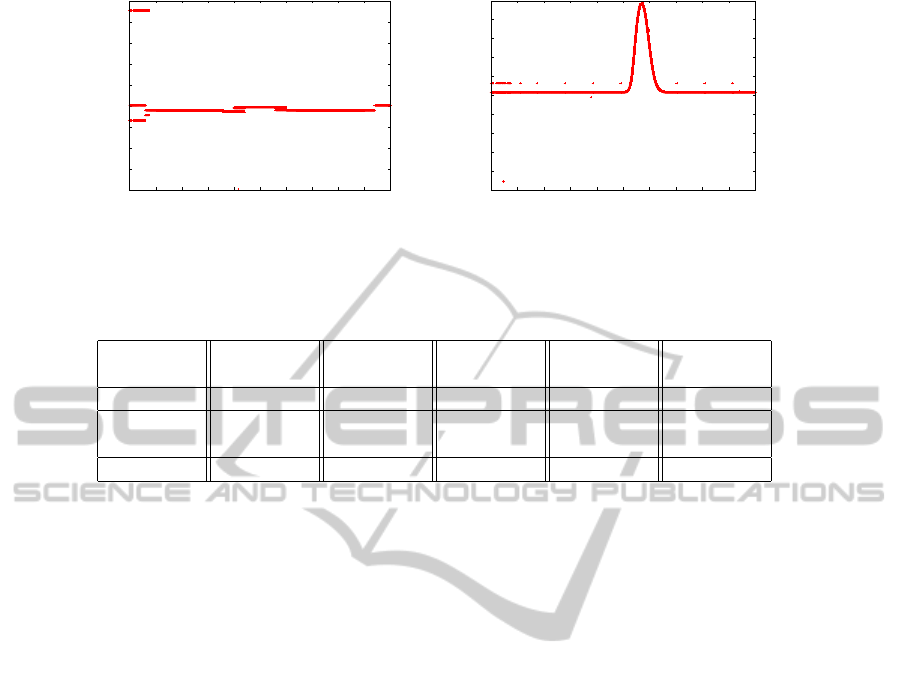
0.51

0.515

0.52

0.525

0.53

0.535

0.54

0.545

0.55

0.555

-5 -4 -3 -2 -1 0 1 2 3 4 5

probability distribution

position x [m]

0.05

0.1

0.15

0.2

0.25

0.3

0.35

0.4

0.45

0.5

0.55

-5 -4 -3 -2 -1 0 1 2 3 4 5

probability distribution

position z [m]

Figure 3: Inﬂuence of the position in the x- and z-axis on the result of the probability distribution. On the left graph it can be

seen, that the position in the x direction has no real inﬂuence on the result of the pre-classiﬁcation. In contrast, the height of

the object inﬂuences strongly their classiﬁcation

Table 1: Result of the semantic labelling algorithm before and after applying the spatial object constraints.

Objects real

objects

feature

evaluation

ﬁnal

result

false

positives

false

negatives

Table 12 13 13 1 0

Flat

screen

9 190 13 9 5

Keyboard 7 6 3 0 4

seen in the Fig. 3. Then, we evaluate the overall re-

sult of the labelling algorithm. For this, we started

it with real scans taken from several ofﬁce rooms of

our institute to check how well the method works. In

these tests, our assumptions were conﬁrmed. Taking

into account the spatial relations between objects im-

proves the result of the labelling signiﬁcantly. This

is because this additional information has a large in-

ﬂuence on the association of the objects to their re-

spective object classes. The result of the experiments

shows that after taking into account this information

many false positives, as in the case of ﬂat screen, re-

sulting from the ﬁrst step are eliminated. In this way,

the recognition result was improved. Table 1 presents

the result of the semantic recognition, before and af-

ter applying the spatial relations between objects. In

the second column the number of ofﬁce objects form

the six real scenes is given. In the next one the rec-

ognized objects, after evaluation of the feature vector,

are presented. It can be seen that many false positives

(e.g. ﬂat screen) have occurred. The fourth column

shows the result after taking into account the spatial

relations between objects. This presents that applying

of the spatial constraints improve the recognition re-

sult, since the number of false recognized ﬂat screens

is reduced.

6 CONCLUSIONS AND FUTURE

WORK

This paper describes our approach for semantic la-

belling of objects from 3D point clouds. This method

combines spatial information about the objects with

their relationships to each other. We showed that

the application of object constraints improves the la-

belling process. This was shown in our experiments

by reduction of false positives. Further, we presented

how probabilistic methods can be used for this issue.

The future work will be mainly on improvement of

the recognition process. We are planning to archive

this by adding probabilistic approaches to the con-

straint checking process. In addition, we would like

to extend our algorithm to other object classes and use

more spatial relations apart from those mentioned in

this paper. Moreover it should handle more complex

objects consist of multiple surfaces. Our goal will be

to extend the approach to other application scenarios,

like kitchens or robots operating in complex environ-

ments that required e.g. stair climbing (Eich et al.,

2008) or deal with outdoor obstacles (Spenneberg and

Kirchner, 2007), (Bartsch et al., 2010).

ACKNOWLEDGEMENTS

This work has been supported by the Graduate School

SyDe, funded by the German Excellence Initiative

SemanticLabellingof3DPointCloudsusingSpatialObjectConstraints

517

within the University of Bremen’s institutional strat-

egy. The project IMPERA is funded by the German

Space Agency (DLR, Grant number: 50RA1111)

with federal funds of the Federal Ministry of Eco-

nomics and Technology (BMWi) in accordance with

the parliamentary resolution of the German Parlia-

ment.

REFERENCES

Anand, A., Koppula, H. S., Joachims, T., and Saxena, A.

(2012). Contextually guided semantic labeling and

search for three-dimensional point clouds. The Inter-

national Journal of Robotics Research.

Aydemir, A., Sj

o, K., and Jensfelt, P. (2010). Object search

on a mobile robot using relational spatial information.

Proc. Int. Conf. on Intelligent Autonomous Systems,

pages 111–120.

Bartsch, S., Birnschein, T., Cordes, F., Kuehn, D., Kamp-

mann, P., Hilljegerdes, J., Planthaber, S., Roemmer-

mann, M., and Kirchner, F. (2010). Spaceclimber: De-

velopment of a six-legged climbing robot for space ex-

ploration. In Robotics (ISR), 2010 41st International

Symposium on and 2010 6th German Conference on

Robotics (ROBOTIK), pages 1–8.

Eich, M., Dabrowska, M., and Kirchner, F. (2010). Seman-

tic labeling: Classiﬁcation of 3d entities based on spa-

tial feature descriptors. In IEEE International Confer-

ence on Robotics and Automation, ICRA.

Eich, M., Grimminger, F., and Kirchner, F. (2008). A versa-

tile stair-climbing robot for search and rescue applica-

tions. In Safety, Security and Rescue Robotics, 2008.

SSRR 2008. IEEE International Workshop on, pages

35–40.

Galindo, C., Fern

andez-Madrigal, J.-A., Gonz

alez, J., and

Safﬁotti, A. (2008). Robot task planning using se-

mantic maps. Robot. Auton. Syst., 56(11):955–966.

Galindo, C., Safﬁotti, A., Coradeschi, S., Buschka,

P., Fern

andez-Madrigal, J., and Gonz

alez, J.

(2005). Multi-hierarchical semantic maps for mo-

bile robotics. In Proc. of the IEEE/RSJ Intl.

Conf. on Intelligent Robots and Systems (IROS),

pages 3492–3497, Edmonton, CA. Online at

http://www.aass.oru.se/∼asafﬁo/.

unther, M., Wiemann, T., Albrecht, S., and Hertzberg, J.

(2011). Model-based object recognition from 3d laser

data. In Proceedings of the 34th Annual German con-

ference on Advances in artiﬁcial intelligence, KI’11,

pages 99–110, Berlin, Heidelberg. Springer-Verlag.

uchter, A. and Hertzberg, J. (2008). Towards semantic

maps for mobile robots. Robotics and Autonomous

Systems, 56(11):915–926.

uchter, A., Surmann, H., Lingemann, K., and Hertzberg, J.

(2003). Semantic scene analysis of scanned 3d indoor

environments. In VMV, pages 215–221.

Pangercic, D., Tenorth, M., Jain, D., and Beetz, M. (2010).

Combining perception and knowledge processing for

everyday manipulation. In Intelligent Robots and Sys-

tems (IROS), 2010 IEEE/RSJ International Confer-

ence on, pages 1065–1071.

Rusu, R., Marton, Z., Blodow, N., Holzbach, A., and Beetz,

M. (2009). Model-based and learned semantic object

labeling in 3d point cloud maps of kitchen environ-

ments. In Intelligent Robots and Systems, 2009. IROS

2009. IEEE/RSJ International Conference on, pages

3601–3608.

Spenneberg, D. and Kirchner, F. (2007). The bio-inspired

scorpion robot: design, control & lessons learned.

Climbing & Walking Robots, Towards New Applica-

tions, pages 197–218.

Vaskevicius, N., Birk, A., Pathak, K., and Poppinga, J.

(2007). Fast Detection of Polygons in 3D Point

Clouds from Noise-Prone Range Sensors. In IEEE In-

ternational Workshop on Safety, Security and Rescue

Robotics, 2007. SSRR 2007, pages 1–6. IEEE Press.

GRAPP2014-InternationalConferenceonComputerGraphicsTheoryandApplications

518