The SITSMining Framework

A Data Mining Approach for Satellite Image Time Series

Bruno F. Amaral

, Daniel Y. T. Chino

, Luciana A. S. Romani

, Renata R. V. Gonc¸alves

Agma J. M. Traina

and Elaine P. M. Sousa

Institute of Mathematics and Computer Science, University of S

ao Paulo, S

ao Carlos, Brazil

Laboratory of New Technologies, Embrapa Agricultural Informatics, Campinas, Brazil

Center of Meteorological and Climate Researches Applied to Agriculture, University of Campinas, Campinas, Brazil

Keywords:

Data Mining, Multivariate Time Series, Remote Sensing, Satellite Image Time Series.

Abstract:

The amount of data generated and stored in many domains has increased in the last years. In remote sensing,

this scenario of bursting data is not different. As the volume of satellite images stored in databases grows,

the demand for computational algorithms that can handle and analyze this volume of data and extract useful

patterns has increased. In this context, the computational support for satellite images data analysis becomes

essential. In this work, we present the SITSMining framework, which applies a methodology based on data

mining techniques to extract patterns and information from time series obtained from satellite images. In

Brazil, as the agricultural production provides great part of the national resources, the analysis of satellite

images is a valuable way to help crops monitoring over seasons, which is an important task to the economy

of the country. Thus, we apply the framework to analyze multitemporal satellite images, aiming to help crop

monitoring and forecasting of Brazilian agriculture.

1 INTRODUCTION

Advances in technologies have led to a rapid increase

in the amount of data generated and stored in several

application domains. In remote sensing, large vol-

umes of complex data, such as satellite images, are ac-

quired from different kinds of orbital sensors in whole

world. In the last decade, the amount of complex data

stored in remote sensing databases has exceeded the

human capacity of manually analyze and extract use-

ful information from these databases. At the same

time, the possibility of exploiting these data in order

to obtain useful information has increased the interest

of the experts. Therefore, new methods available in

computational tools are needed to allow the analysis

of big volumes of complex data, in order to discover

valuable information and knowledge.

Satellite images have been widely used to study

land surface, such as identiﬁcation of forest, water, ur-

ban areas, as well as for meteorological applications.

However, if manually performed, these studies can be

very time consuming for the experts, and therefore al-

most impracticable. To overcome this problem, many

computational techniques can be applied to perform

this analysis in feasible time.

A common approach to satellite image analysis is

to extract the pixel values from a single image and

apply data mining techniques, such as clustering or

classiﬁcation, to group similar pixels or to label every

pixel of the image in order to identify areas of interest.

This approach is very used in agriculture, in which

the task consists in labeling each pixel (or a group

of pixels) of one satellite image based on its value,

aiming to identify one or more types of crop areas,

such as sugar cane or coffee.

We focus on a different approach, based on the

analysis of time series extracted from satellite image

time series (SITS), which is a sequence of satellite

images taken from the same scene. Therefore, a time

series is obtained for each pixel, such that each data

point corresponds to the pixel value in one image of

the SITS. We can thus grasp the information related

to the behavior of each area in the images along time,

and analyze it using data mining techniques, such as

clustering (Kyrgyzov et al., 2007) and classiﬁcation

(Vaduva et al., 2011). The analysis of SITS using data

mining is useful in agriculture, for example, for crops

monitoring along seasons (Julea et al., 2011).

We propose a framework to allow the analysis of

time series obtained from multitemporal satellite im-

225

F. Amaral B., Y. T. Chino D., A. S. Romani L., R. V. Gonçalves R., J. M. Traina A. and P. M. Sousa E..

The SITSMining Framework - A Data Mining Approach for Satellite Image Time Series.

DOI: 10.5220/0004894002250232

In Proceedings of the 16th International Conference on Enterprise Information Systems (ICEIS-2014), pages 225-232

ISBN: 978-989-758-027-7

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

ages through data mining methods. Initially, a dataset

is extracted from satellite imagery time series, con-

sidering a region of interest provided by the user. As

the framework uses the time series approach, for each

area of the region of interest, one or more time series

can be extracted from the satellite images. Therefore,

a real area can be analyzed based on different aspects,

such as surface temperature and vegetation index, for

example. Then, data mining tasks, such as classiﬁ-

cation and clustering, can be applied to classify or

cluster the region of interest. Finally, the framework

provides an appropriately formatted output for the ex-

perts, that allows a proper visualization of the results,

such as spatial geographic visualization.

We also show experimental studies of applying the

framework to classify and cluster the Sao Paulo state,

Brazil, for agricultural purposes. These tests produce

useful results for the expert analysis, as they provide a

geographic visualization of the data mining output, al-

lowing the experts to identify areas such as sugarcane

crops, forest, rivers and urban areas. Also, represen-

tative time series of each pattern (class or cluster) are

returned, which are essential to understand the behav-

ior of the areas associated to the patterns, over time.

The paper is organized as follows. Section 2 gives

background concepts. In Section 3 we detail the pro-

posed framework. Experimental studies performed on

the framework basis are described in Section 4 and

Section 5 concludes the paper.

2 BACKGROUND

Temporal Data Mining. A time series can be de-

ﬁned as ordered numeric measurements at regular

time intervals (Mitsa, 2010). A time series T =

,...,t

} can be univariate or multivariate. A

data point t

of a univariate time series is an one-

dimensional real value, i.e., t

∈ R. If T is a multi-

variate or multidimensional time series, each point t

is a D-dimensional vector, i.e., t

∈ R

, with D > 1.

Time series datasets are presented in many appli-

cation domains, and because of its ubiquity and ex-

ponentially growing size of databases in recent years,

there has been an explosion of interest in knowledge

discovery and data mining techniques for time series

analysis (Maimon and Rokach, 2005).

Nowadays, time series are used in domains such as

medicine (electrocardiograms and electroencephalog-

raphy), ﬁnances (sequences of stock values over a

period of time in stock market) and agrometeorol-

ogy (historical series of rainfall or series of crop pro-

duction). The main tasks in temporal data mining

are (Maimon and Rokach, 2005): classiﬁcation, clus-

tering, prediction, indexing, summarization, anomaly

detection and segmentation. In this work, we focus

on time series classiﬁcation and clustering.

Clustering is the process of grouping sets of ob-

jects based on their similarity, so that one object is

more similar to another object of the same cluster, and

less similar to an object of a different cluster, accord-

ing to a given distance function (Han and Kamber,

2000). Clustering is an unsupervised learning task,

i.e., only the dataset is necessary and no additional in-

formation about the data is needed. To perform time

series clustering, the use of a distance function com-

patible with time series is required.

Classiﬁcation is a supervised or semi-supervised

learning task, which means some kind of knowledge

about the data must be provided, in most cases, by

the domain experts (Mitsa, 2010). This supervised

information corresponds to the training set, a set of

examples previously labeled. The classiﬁcation pro-

cess occurs in two steps (Han and Kamber, 2000): 1)

construction of a model (or classiﬁer) that describes a

predetermined set of classes or concepts, based on the

training set examples; 2) the model is used to classify

unlabeled objects in the dataset. In most classiﬁcation

methods, a distance function is needed to calculate

distance values between objects. In most cases, if the

distance function is compatible with time series, the

method can be applied for time series classiﬁcation.

Distance function is generally used to measure

the dissimilarity between two time series. One of

the most widely used is the Euclidean distance (L

Given two time series A = {a

,...,a

} and B =

,...,b

}, L

is deﬁned by:

(A,B) =

∑

i=1

− b

)

(1)

It is important to note that the Euclidean distance

is also suitable for multivariate time series. If A and B

are multivariate time series, the Equation 1 is calcu-

lated considering data points a

and b

as multidimen-

sional vectors, instead of one-dimensional vectors.

However, Euclidean distance cannot be used to

calculate the dissimilarity between two time series

with different lengths. To overcome this problem, the

well-known Dynamic Time Warping (DTW) (Berndt

and Clifford, 1994) function seeks to calculate the

similarity between two time series by performing the

alignment among different pairs of data points. Thus,

if two time series have similar shapes but are not

aligned in the time axis, DTW can still recognize their

similarity. Since DTW calculates the distance be-

tween pairs of data points using Euclidean distance,

it can also be applied to multivariate time series.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

226

Another distance function suitable for time series

of different lengths is the Longest Common Subse-

quence (LCSS) (Vlachos et al., 2003). The LCSS ob-

jective is to return the size of the longest common sub-

sequence between two time series, so that the larger

this size is, the more similar are the two time series.

Since time series are real valued, a threshold value e

is needed, and a pair (a

) is considered common if

the Euclidean distance L

) < e. The LCSS can

also deal with multivariate time series.

Satellite Images. The potential of multitempo-

ral satellite images to support research of meteorol-

ogy, agricultural monitoring, environment and urban-

ism has increased according to improvements in tech-

nological development, especially in analysis of large

volume of data available for knowledge discovery.

Several satellites can be used to help the monitor-

ing and estimation of agricultural production, such

as crop area and yield estimation; climate applica-

tions as well as forecasting and weather monitoring;

and land surface study. These application have used

specially satellites which have low spatial resolution

and high temporal resolution images, for example, the

National Oceanic and Atmospheric Administration

(NOAA), with its Advanced Very High Resolution

Radiometer (AVHRR) sensor; the satellite TERRA -

Earth Observing System (EOS) with Moderate Res-

olution Imaging Spectroradiometer (MODIS) sensor;

and SPOT Vegetation (Satellite Pour l’Observation de

la Terre Vegetation).

Due to availability of daily images since 1970,

specialists have historical series and use images from

different satellites. These sensors are applied to stud-

ies of ecosystems and long time series of data have

been used to support researches in a regional scale for

a longer period of time. Additional advantages are

global coverage and free access to data. Moreover,

by combining different satellite channels it is possible

to generate synthesis images such as the Normalized

Difference Vegetation Index (NDVI) (Rouse et al.,

1973), which is strongly correlated with biomass.

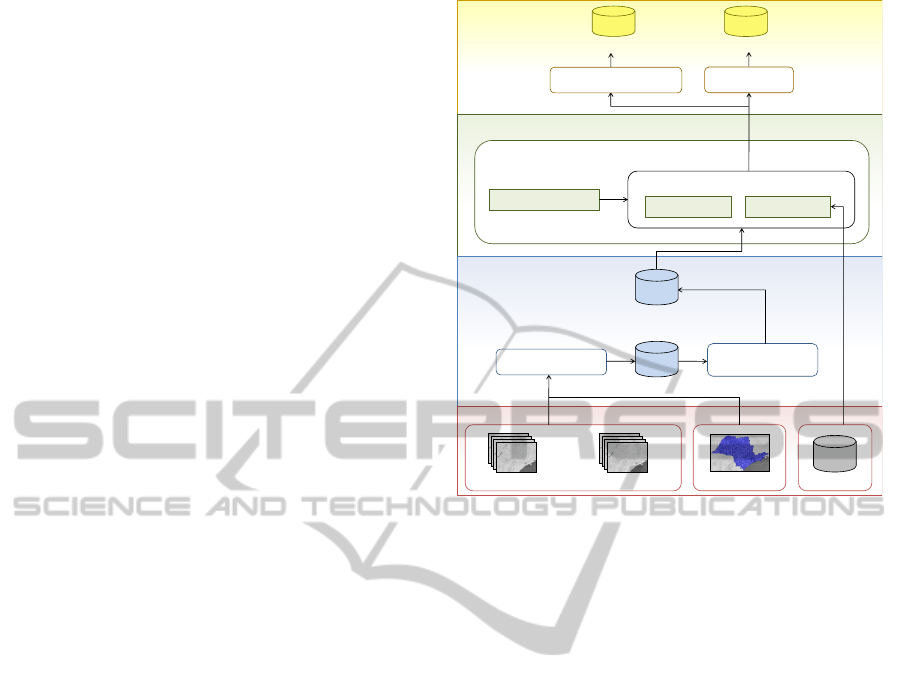
3 OUR FRAMEWORK

We propose a framework to analyze SITS using

data mining techniques. The SITSMining framework

(Satellite Image Time Series Mining) is organized

into three layers: Extraction and Preprocessing, Data

Mining and Output, as shown in Figure 1. Each layer

is composed by one or more modules, detailed in the

following sections. The framework input includes

SITS, regions of interest and training set, as follows:

• Satellite Image Time Series (SITS): a set of D

Image Time Series 1

...

Training Set

Region of Interest

Input

Image Time Series D

Extraction and

Preprocessing Layer

Data Mining Layer

Output Layer

Extraction Module

Data set

Preprocessing

Module

Preprocessed

Data set

Data Mining Module

ClassificationClustering

Distance Functions

Data Mining Methods

Spatialization Module

Profile Module

Geographic Spatial Output Profile Output

Figure 1: Framework components and data ﬂow.

series of n satellite images. Each image must have

been already preprocessed and georeferenced to

allow further data extraction. Also, each series

should have images of the same type, ordered in

time scale and acquired in regular time intervals.

• Region of Interest: a list of p pairs of latitude

and longitude coordinates indicating the region of

interest. Each pair of coordinates references one

single pixel of image, from which the data will be

extracted. Note that the region of interest is the

same for all images of the time series.

• Training Set (for Classiﬁcation Task): a set of

m elements composed by two attributes: 1) a mul-

tivariate time series and 2) a label value. Also, the

training set can hold the information of latitude

and longitude for every element, if they have been

extracted from pixels of satellite images.

Initially, the region of interest, which contains the

coordinates of the real areas we want to analyze, are

combined with the satellite image time series, so we

can identify the pixels related to those areas in each

image of the series, and extract data from them. In

the Extraction and Preprocessing Layer, the data is

extracted from the satellite images, and the dataset is

preprocessed in order to remove noises and normalize

the time series. The preprocessed dataset is then sent

to the Data Mining Layer, where the data mining anal-

ysis is performed. It is important to note that the train-

ing set, given as input will only be used in the Data

Mining Layer. Finally, the Output Layer receives the

TheSITSMiningFramework-ADataMiningApproachforSatelliteImageTimeSeries

227

Extraction and Preprocessing Layer

1 -22.300881 -52.660943 ...

2 -21.065848 -48.476518 ...

p -22.878558 -44.470575 ...

...

Multivariate

Time Series

...

Extraction Module

Index Values Extraction

Dataset Creation

Preprocessing Module

Noise Treatment

Time Series Normalization

Dataset

Latitude Longitude

T1 T2

...

Figure 2: Extraction and Preprocessing Layer modules and the dataset structure.

data mining results and yields formatted outputs that

allow useful visualization of the discovered patterns,

such as spatial visualization of clusters.

3.1 Extraction and Preprocessing Layer

The Extraction and Preprocessing Layer consists of

two main modules, as illustrated in Figure 2: 1) ex-

traction module and 2) preprocessing module.

The extraction module is responsible for extract-

ing the real valued time series from the input SITS

and building the dataset that will be used along the en-

tire framework. Each dataset element is created based

on one pair of coordinates of the region of interest,

by extracting data from the pixel referenced by these

coordinates, in all images of the series. For all el-

ements, one real value is obtained from each image

given as input, and these values are organized as time

series. The time series data points extracted from the

image series are calculated using indices, such as veg-

etation indices. This extraction can be performed us-

ing softwares such as ENVI

or libraries that work

with geospatial data, such as GDAL

The index to be used depends on the type of satel-

lite image analyzed, and should be provided by ex-

perts in the domain of application.

The attributes of each element are (Figure 2):

• Id: an integer value used to identify the element

in the dataset.

• Latitude: the latitude coordinate of the area rep-

resented by the selected pixel.

• Longitude: the longitude coordinate of the area

represented by the selected pixel.

• Multivariate Time Series: a multivariate

time series is extracted from the SITS:

http://www.exelisvis.com

http://www.gdal.org/

T = {t

,...,t

}, with i ∈ [1,n], in which

correspond to a D-dimensional vector, whose

data points t

i j

, j ∈ [1,D], indicates the value of

the selected pixel in the image i of the SITS j.

After building the dataset, the data is forwarded

to the preprocessing module. In satellite images, the

occurrence of noise caused by failures in the measure-

ment process, or presence of clouds over the area of

interest is very common and even expected by the ex-

perts. In the resulting time series t

, noise can be read

as a very high or low unusual real value, or a spe-

ciﬁc value returned by the sensor, that indicates the

reading error. Here, we are interested in replacing the

noise with valid values instead of removing it, so we

can keep the corresponding time series complete. In

this case, one possible approach is to use a technique

to ﬁll in the noisy value with an estimate (Keogh and

Pazzani, 1998).

Another issue treated in the preprocessing mod-

ule is the time series normalization. Since each image

time series may have been deﬁned by a different type

of image, the extraction of the corresponding indices

may result in time series with distinct ranges of val-

ues. Thus, all time series values are normalized, mak-

ing them comparable when using a distance function

appropriate to multivariate time series.

In some studies (Freitas et al., 2011), outliers de-

tection and smoothing techniques are applied to re-

place outliers by new values that ﬁt under a smoother

time series or function. In our framework, we main-

tain these outliers, because in some domains of appli-

cation, the uncommon behavior of the original time

series extracted from the satellite images can be use-

ful to the data mining analysis, such as clustering or

classiﬁcation.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

228

Data Mining Layer

Data Mining Module

Clustering Methods

Classification Methods

Supervised Classification

Semi-supervised Classification

Distance Functions

Figure 3: Data Mining Layer and its components.

3.2 Data Mining Layer

Initially, in the Data Mining Layer, two data mining

tasks are implemented: clustering and classiﬁcation.

Each task has a speciﬁc submodule and allows the ad-

dition of new data mining algorithms at anytime. Fig-

ure 3 illustrates the data mining module.

The classiﬁcation submodule includes supervised

and semi-supervised classiﬁcation methods. Despite

the differences between these two classiﬁcation ap-

proaches, both receive the dataset and the training set

as input, and assign a label value to each dataset ele-

ment, corresponding to its class value. In the cluster-

ing analysis, only the dataset is needed as input, and

the output yielded indicates the cluster each dataset

element is assigned to.

Most classiﬁcation and clustering methods require

a distance function to calculate the dissimilarity be-

tween pairs of objects. In our framework, the dis-

tance functions need to be compatible with multi-

variate time series, such as the Euclidean distance,

DTW and LCSS. Other multivariate time series dis-

tance functions can be added in the distance function

submodule at anytime.

3.3 Output Layer

The data mining results are sent to the Output Layer,

where they are transformed into two different types of

formatted output: spatial visualization (spatialization

module) and proﬁle visualization (proﬁle module), as

shown in Figure 4.

The spatialization module produce an output that

allows a geographic spatial visualization of the re-

sults, in which each pixel of the region of interest

is plotted based on its latitude and longitude values,

and colored according to the label assigned to it in

the data mining process (the label could be a cluster

or class value). Therefore, the output of the spatial-

ization module is a set of p elements, with three at-

tributes: 1) latitude; 2) longitude; and 3) label. This

visualization is useful to the experts analysis, because

they are able to view the geographic spatial display of

the patterns found in the data mining process.

In the proﬁle module, for each cluster or class

present in the data mining results, the objective is to

Output Layer

Spatialization Module

Profile Module

Class 1 ...

...

Label

...

-22.300881 -52.660943 Class 2

-21.065848 -48.476518 Class 1

-22.878558 -44.470575 Class 3

...

Latitude

Representative multivariate time

series for pattern ‘Class C’

Class 2 ...

Class C ...

Multivariate Time

Series

...

Longitude

Label

Figure 4: Output Layer modules and the output structure.

plot a representative time series proﬁle. In the clus-

tering analysis, a representative proﬁle to the cluster

could be its centroid or medoid, or an average valued

time series for each class, in the classiﬁcation case.

To provide this type of visualization, the output must

hold, for each pattern, the label related to it, and the

multivariate representative time series calculated for

this pattern. Figure 4 shows the structured outputs

yielded by the two modules of the Output Layer.

A SITSMining framework prototype is being de-

veloped as an extension of the SatImagExplorer sys-

tem, a tool to extract time series from a SITS, analyze

these temporal data and visualize the results geospa-

tially (Chino et al., 2011). The SatImagExplorer sys-

tem was developed using C++ and the Qt framework

and is organized in a modular architecture. Once the

tool provides the extraction and visualization func-

tions, we intend to implement the SITSMining frame-

work into the SatImagExplorer system, so the entire

process, as well as the input and output of the frame-

work can be handled under the same platform.

As the current version of the SatImagExplorer al-

lows the user to open only one sequence of satel-

lite images to the extraction of time series, it yields

one univariate time series per coordinate of the im-

ages. Thus, the tool is currently limited to the one-

dimensional time series case. We aim to extend the

tool features, in order to allow the extraction of mul-

tidimensional time series from many satellite image

time series. In the next section, we show experiments

based on the SITSMining framework and its current

prototype implemented in SatImagExplorer.

4 EXPERIMENTAL RESULTS

We performed experimental studies in order to show

the utility of the proposed framework analysis and its

applicability to real domains such as agriculture. For

http://qt.digia.com

TheSITSMiningFramework-ADataMiningApproachforSatelliteImageTimeSeries

229

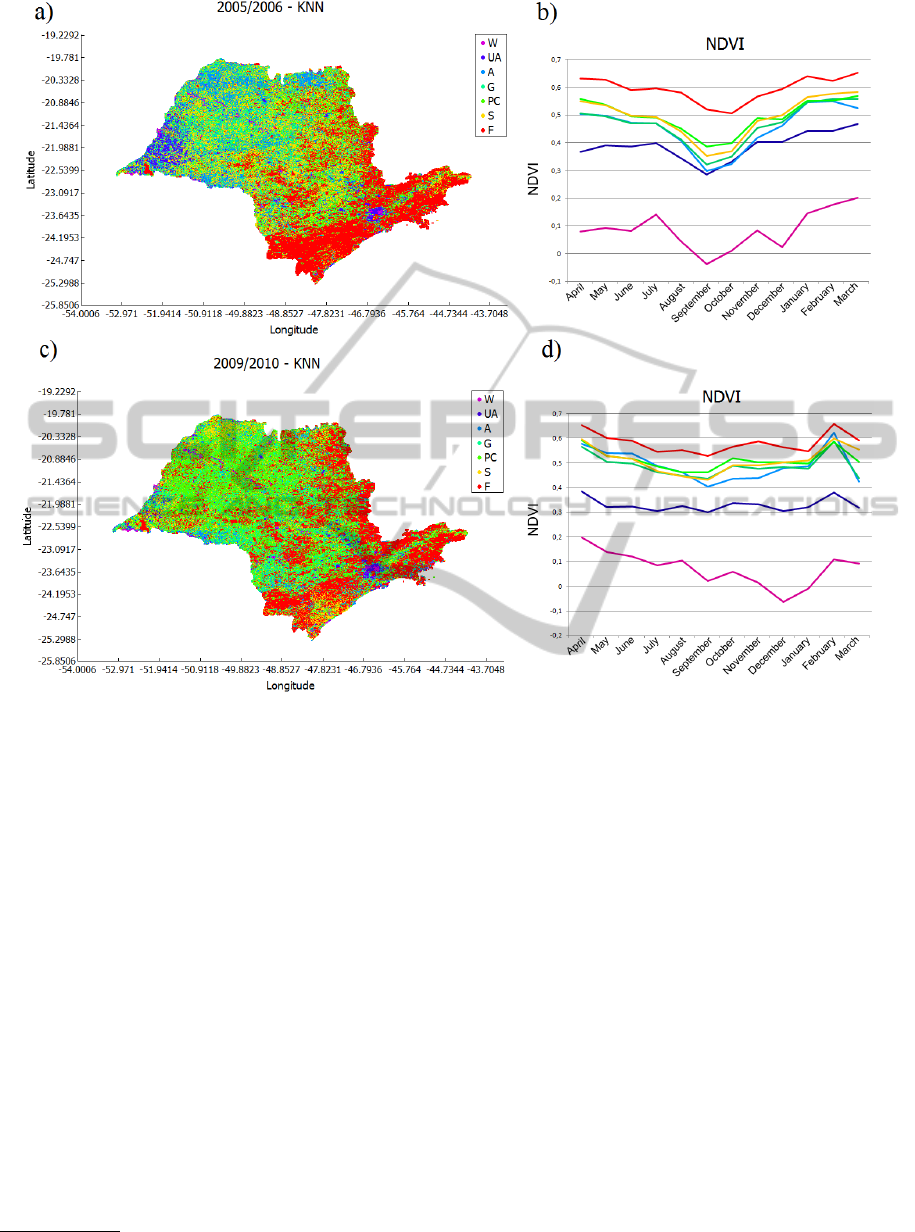
Figure 5: Geographic spatial and proﬁle visualization of classiﬁcation results.

the data mining analysis, two traditional algorithms,

K-Means and KNN (K-Nearest-Neighbors) (Han and

Kamber, 2000), were used. It is important to note that

the objective of the experiments was not to perform a

comparison between the algorithms, but to show the

potential of the data mining analysis combined with

the SITSMining framework.

The satellite images we studied were generated

by AVHRR sensors, aboard of NOAA satellites, and

have low spatial resolution, each pixel corresponding

to a 1km

real area. The region of interest is com-

posed by 220,238 pairs of coordinates and refers to

the Sao Paulo state, Brazil.

Three types of AVHRR/NOAA images were con-

sidered

: NDVI, Albedo and Surface Temperature.

The NDVI is a vegetation index widely used in agri-

culture, because it indicates biomass values of a given

area. In forest areas, for example, NDVI values are

usually very high, in contrast to urban or soil areas,

that present low NDVI. Albedo measures the level of

Satellite images provided by CEPAGRI-UNICAMP.

light reﬂectivity of a given area (Csiszar and Gutman,

1999). Considering these three satellite image time

series, two experiments were performed:

• Experiment 1: classiﬁcation of one-dimensional

(univariate) time series datasets, extracted from

NDVI SITS, using algorithm KNN with DTW.

• Experiment 2: clustering of two-dimensional

(multivariate) time series datasets, extracted from

Albedo and Surface Temperature SITS, using al-

gorithm K-Means with DTW.

For each experiment, two datasets were used,

considering two different sugarcane crop seasons:

2005/2006 and 2009/2010. For each season, twelve

monthly satellite images were considered, corre-

sponding to a one-year period, totalizing 12 data

points for each time series, from April to March.

In the ﬁrst experiment, as required for the classiﬁ-

cation task, we used a training set provided by experts

in agrometeorology, containing 65 examples of 7 dif-

ferent types of areas:

• Water (W): 6 examples.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

230

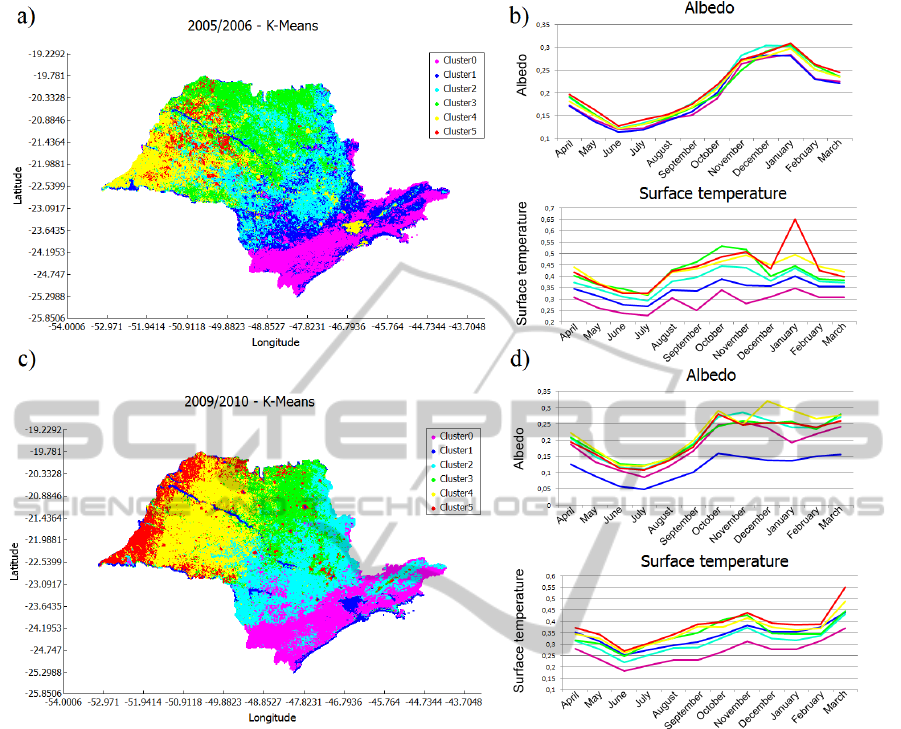
Figure 6: Geographic spatial and proﬁle visualization of clustering results.

• Urban area (UA): 10 examples.

• Agriculture (A): 9 examples.

• Grassland (G): 14 examples.

• Perennial Crop (PC): 9 examples.

• Sugarcane (S): 8 examples.

• Forest (F): 9 examples.

Besides the class (or label) value, the training

set examples have the same attributes as the dataset

NDVI elements, which contains a pair of coordinates

(latitude and longitude) and a one-dimensional NDVI

time series of length 12. Figure 5 illustrates the clas-

siﬁcation results of the ﬁrst experiment. The spatial

geographic visualization of the labeled areas in Sao

Paulo state is shown in Figure 5a) and c) and the pro-

ﬁle visualization is shown in Figure 5b) and d) for the

2005/2006 and 2009/2010 season, respectively. The

average time series of each class were chosen as rep-

resentative for the proﬁle visualization.

In the classiﬁcation analysis, Forest (F), Urban

area (UA) and Water (W) areas were correctly la-

beled, according to the experts. Most of the Atlantic

Forest, located near to the Sao Paulo state coast (at

southeast) was assigned to the Forest class, repre-

sented by the red colored pixels of the spatial geo-

graphic visualization. As forests have high concen-

tration of vegetation and biomass, these areas present

elevated NDVI values the whole season, as shown by

the red colored representative time series, in the pro-

ﬁle visualization. On the other hand, urban and wa-

ter areas, represented by the purple and pink proﬁles,

present low NDVI values along the entire year due to

their lack of vegetation concentration.

The classiﬁcation results for the tillable areas

(Agriculture, Perennial crop and Sugarcane) and

Grassland were less accurate, probably because dif-

ferent crops present similar NDVI values at some

phase in the vegetative crop cycle. According to the

experts, even with some labeling mistakes, the clas-

TheSITSMiningFramework-ADataMiningApproachforSatelliteImageTimeSeries

231

siﬁcation analysis is useful because it was possible

to separate agricultural areas from non-agricultural,

such as water, forest and urban areas.

In the second experiment, we performed the clus-

tering analysis of the same datasets. The spatial geo-

graphic visualization of the clustering results is shown

in Figure 6a) and c) and the proﬁle visualization is

shown in Figure 6b) and d). The representative time

series chosen were the centroid of each cluster.

According to the experts, the Albedo variable was

useful to separate water areas from the other targets,

but was not sufﬁcient to distinguish areas with differ-

ent vegetation cover. The clustering of the other areas

was deﬁned mainly by the Surface Temperature vari-

able, being higher for targets with lower canopy, for

example, urban areas and exposed soil, and lower for

forest regions, such as the Atlantic Forest areas. The

cluster conﬁguration varied from year to year because

the weather also varied over the last decade, inﬂuenc-

ing the values of Surface Temperature.

5 CONCLUSION

This paper presented the SITSMining framework, an

automated solution to data mining based analysis of

satellite image time series. As the need for knowledge

discovery in large remote sensing databases grows,

the framework is shown as a powerful computational

tool for the experts, as it provides resources such as

data extraction from multitemporal satellite images,

analysis of large datasets through data mining tech-

niques and output formatting in an integrated environ-

ment. Because of its modular architecture, the frame-

work allows the addition of new methods for noise

replacement, classiﬁcation and clustering based anal-

ysis, output formatting, as well as the incorporation

of new data mining task modules.

The experimental analysis performed shows that

the framework is useful to support researches in agri-

culture domain of application, even considering low

spatial resolution satellite images. In future work, we

aim to fully integrate the SITSMining framework to

the SatImagExplorer tool, to provide for the experts

in agrometeorology, the possibility to perform extrac-

tion of time series from multitemporal satellite im-

ages, data mining analysis and output visualization in

an integrated system under the same platform.

ACKNOWLEDGEMENTS

We thank to CNPq, FAPESP, CAPES, Embrapa-

Campinas for ﬁnancial support.

REFERENCES

Berndt, D. and Clifford, J. (1994). Using dynamic time

warping to ﬁnd patterns in time series. In AAAI Work-

shop on Knowledge Discovery in Databases, pages

359–370, Seattle - Washington.

Chino, D. Y. T., Amaral, B. F., Romani, L. A. S., Sousa, E.

P. M., and Traina, A. J. M. (2011). Satimagexplorer:

tornando a minerac¸

ao de dados de sensores orbitais

mais ﬂex

ıvel. In VIII SBBD, pages 25–30, Brasil.

Csiszar, I. and Gutman, G. (1999). Mapping global land

surface albedo from noaa avhrr. Journal of Geophysi-

cal Research, 104(d6):6215–6228.

Freitas, R. M., Arai, E., Adami, M., Souza, A. F., Sato, F. Y.,

Shimabukuro, Y. E., Rosa, R. R., Anderson, L. O., and

Rudorff, B. F. T. (2011). Virtual laboratory of remote

sensing time series: visualization of modis evi2 data

set over south america. Journal of Computational In-

terdisciplinary Sciences, 2(1):57–68.

Han, J. and Kamber, M. (2000). Data Mining: Concepts

and Techniques. Morgan Kaufmann, San Francisco.

Julea, A., M

eger, N., Bolon, P., Rigotti, C., Doin, M.-P.,

Lasserre, C., Trouv

e, E., and Lazarescu, V. N. (2011).

Unsupervised spatiotemporal mining of satellite im-

age time series using grouped frequent sequential pat-

terns. Geoscience and Remote Sensing, IEEE Trans-

actions on, 49(4):1417–1430.

Keogh, E. J. and Pazzani, M. J. (1998). An enhanced repre-

sentation of time series which allows fast and accurate

classiﬁcation, clustering and relevance feedback. In

KDD 1998, volume 98, pages 239–243.

Kyrgyzov, I. O., Maitre, H., and Campedel, M. (2007). A

method of clustering combination applied to satellite

image analysis. In Image Analysis and Processing,

2007. 14th International Conference on, pages 81–86.

Maimon, O. and Rokach, L. (2005). The Data Mining and

Knowledge Discovery Handbook. Springer.

Mitsa, T. (2010). Temporal Data Mining. Chapman &

Hall/CRC, 1st edition.

Rouse, J. W., Haas, R. H., Schell, J. A., and Deering, D. W.

(1973). Monitoring vegetation systems in the Great

Plains with ERTS, volume 1, pages 309–317. NASA.

Vaduva, C., Costachioiu, T., Patrascu, C., Gavat, I.,

Lazarescu, V., and Datcu, M. (2011). Classiﬁcation of

dynamic evolutions from satellitar image time series

based on similarity measures. In Analysis of Multi-

temporal Remote Sensing Images (Multi-Temp), 2011

6th International Workshop on the, pages 141–144.

Vlachos, M., Hadjieleftheriou, M., Gunopulos, D., and

Keogh, E. (2003). Indexing multi-dimensional time-

series with support for multiple distance measures. In

KDD 2003, pages 216–225, New York.

ICEIS2014-16thInternationalConferenceonEnterpriseInformationSystems

232