Quantum Probability in Operant Conditioning
Behavioral Uncertainty in Reinforcement Learning
Eduardo Alonso
1,2
and Esther Mondragón
2
1
Department of Computer Science, City University London, London EC1V 0HB, U.K.
2
Centre for Computational and Animal Research Centre, St. Albans AL1 1RQ, U.K.
Keywords: Operant Conditioning, Reinforcement Learning, Uncertainty, Quantum Probability, Classical Probability.
Abstract: An implicit assumption in the study of operant conditioning and reinforcement learning is that behavior is
stochastic, in that it depends on the probability that an outcome follows a response and on how the presence
or absence of the output affects the frequency of the response. In this paper we argue that classical
probability is not the right tool to represent uncertainty operant conditioning and propose an interpretation
of behavioral states in terms of quantum probability instead.
1 INTRODUCTION
Operant conditioning, how animals learn the relation
between their behavior (responses) and its
consequences (outcomes) is explained in reference
to two dimensions, namely, whether the outcome
follows the response and whether the frequency of
the response increases or decreases subsequently
(Skinner, 1938). If the outcome follows the
response, the relation is positive; and negative if it
does not. If the frequency of the response increases,
we call it reinforcement; if it decreases, punishment.
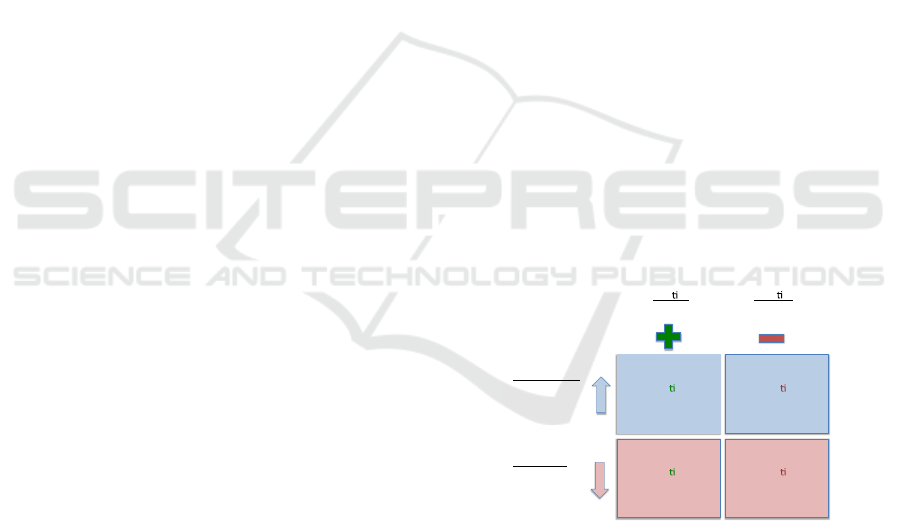
Thus, as illustrated in Fig. 1, there are four
fundamental conditioning procedures:
Positive reinforcement: The response is
followed by an outcome that is appetitive,
increasing the response frequency. For instance,
food follows pressing a lever.
Negative reinforcement: The response is not
followed by the outcome, increasing the
response frequency. For instance, pressing the
lever removes an aversive output such as a loud
noise.
Positive punishment: The response is followed
by the outcome, decreasing the response
frequency. For instance, pressing a lever is
followed by an electric shock.
Negative punishment: The response is not
followed by the outcome, decreasing the
response frequency. For instance, removing ad
libitum food when pressing the lever.
Figure 1: Operant conditioning procedures.
This interpretation of associative learning has
been borrowed in Artificial Intelligence, in particular
in modeling reinforcement learning, where an agent
learns by interacting with its environment in the
form rewards (Sutton and Barto, 1998). In
reinforcement learning, positive and negative
outputs are defined as scalar rewards. It is assumed
that those behaviors that are predicted to obtain
higher accumulative reward will be elicited more
frequently. One of the main issues in modeling
operant conditioning and reinforcement learning is
to represent the inherent uncertainty animals and
software agents face accurately. In this paper we
present a formalization of uncertainty in terms of
quantum probabilities, which solve some issues that
arise with classical and Bayesian probabilities
typically associated with operant conditioning and
reinforcement learning.
Posi ve
Reinforcement
Nega ve
Reinforcement
Posi ve
Punishment
Nega ve
Punishment
Posi ve
Applies
output
Nega ve
Removes
output
Reinforcement
Increases
frequency
of
behavior
Punishment
Decreases
frequency
of
behavior
548
Alonso E. and Mondragon E..
Quantum Probability in Operant Conditioning - Behavioral Uncertainty in Reinforcement Learning.
DOI: 10.5220/0004903205480551
In Proceedings of the 6th International Conference on Agents and Artificial Intelligence (ICAART-2014), pages 548-551
ISBN: 978-989-758-015-4
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 BASIS VECTORS AND
BEHAVIORAL STATE
In quantum probability theory a vector space
(technically, a Hilbert space) represents all possible
outcomes for questions we could ask about a system.
A basis is a set of linearly independent vectors that,
in linear combination, can represent every vector in
the vector space. They represent the coordinate
system and correspond to elementary observations.
Put it another way, the intersection of all subspaces
containing the basis vectors, that is, their linear span,
constitutes the vector space. A vector represents the
state of the system, given by the superposition of the
basis vectors according to their coefficients (Hughes,
1989; Isham, 1989). Historically, quantum
probability has been applied to physical systems but
the same analysis can refer to other types of systems,
including animals and software agents. At the end of
the day, animals are behavior systems –sets of
behaviors that are organized around biological
functions and goals, e.g., feeding (Timberlake and
Silva, 1995), defense (Fanselow, 1994), or sex
(Domjan, 1994). Software agents, on the other hand,
are formally defined as systems that (learn to) act in
virtual environments. Not surprisingly,
reinforcement learning in software agents has taken
concepts and methods from operant conditioning
theory. In turn, the former, software learning agents,
can be understood as computational models of the
latter, operant conditioning.
We define two basis vectors according to the
dichotomies reinforcement vs. punishment and
positive vs. negative in Fig. 1. The former, that we
call Frequency, takes values ranging from a
maximum number of responses per unit time
(Reinforcement) to the absence of response
(Punishment); the latter, that we call Applies, takes
values from “the response always applies the
outcome” (Positive) to “the response always
removes the outcome” (Negative). The values in
between indicate various response frequencies, that
is, probabilities that the animal responds, and
various probabilities that the outcome follows the
response, respectively.
The relation of the two bases is undetermined, in
the sense that even in the simplest reinforcement
schedules (fixed/variable ratio/interval schedules)
we cannot observe with certainty how the response
affects the outcome and how the outcome affects the
frequency of responding at the same time. This
uncertainty is aggravated in more complex
compound schedules.
The problem is thus how to determine the
behavioral state of an animal given this uncertainty.
Several models have been proposed to explain
patterns of operant behavior, some of which use
probabilities (see (Staddon and Cerutti, 2003) for a
recent survey). We argue that the inherent
uncertainty in operant conditioning cannot be
represented using classical probability (Kolmogorov,
1933), and that we need quantum probability
instead.
The behavioral state of the animal is represented
using the state vector, a unit length vector, denoted
as |Ψ in bra-ket notation. We need to find out which
linear combination of the basis vectors results in a
given behavioral state and with which probability.
We start with a single question in Fig. 2, about
whether the response applies the outcome. In this
case |Positive and |Negative are the basis states, so
we can write |Ψ = a|Positive + b|Negative
, where
“a” and “b” are amplitudes (coefficients) that reflect
the components of the state vector along the
different basis vectors. The answer to the question is
certain when the state vector |Ψ exactly coincides
with one basis vector. For instance if “the response
always applies the outcome”, then |Ψ = |Positive.
In such case the probability of Positive is 1. Since
the basis vectors are orthogonal, that is, since they
represent mutually exclusive answers, we know that
“the response removes the outcome” with 0
probability, corresponding to a 0 projection to the
subspace for Negative.
Figure 2: State space with the Applies subspace
(corresponding to the question whether response applies
outcome) and Positive-Negative basis vectors. The blue
vertical line represents the projection of |Ψ on |Positive.
To determine the probability of Positive we use a
projector, P
Positive
, which takes the vector |Ψ and
lays it down on the subspace spanned by |Positive,
that is, P
Positive
|Ψ = a|Positive. Then, the probability
that the response applies the outcome is equal to the
squared length of the projection, ||P
Positive
|Ψ||
2
. The
same applies to the probability associated with
b|Negative.
Posi ve
Nega ve
Ψ
(a)
QuantumProbabilityinOperantConditioning-BehavioralUncertaintyinReinforcementLearning
549

3 COMPATIBILITY
In operant conditioning we are interested in two
questions, whether the response applies the outcome,
and whether the response frequency increases, each
with two possible answers: Positive and Negative to
the question “Applies”, and Reinforcement and
Punishment to “Frequency”. Crucially for our
analysis, these questions are incompatible. For
compatible questions, we can specify a joint
probability function for all combinations of answers,
and in such cases the predictions of classical
probability and quantum probability theories are the
same. By contrast, for incompatible questions, it is
impossible to determine the answers concurrently.
Being certain about the answer of one question
induces an indeterminate state regarding the answers
of other, incompatible questions. This is the case in
operant conditioning: We cannot observe at the same
time whether an outcome follows from a response
and whether the response follows from the outcome,
that is, whether the response frequency increases.
Classical probability does not apply to incompatible
questions.
Figure 3: State space including the Frequency subspace
with the Reinforcement (increases)-Punishment
(decreases) basis vectors.
Mathematically, incompatibility means that
subspaces exist at non-orthogonal angles to each
other, as in the sub-spaces in Fig. 3. Hence, since
certainty about a possible answer means that the
state vector is contained within the subspace for the
answer, if we are certain that Applies holds, then the
state vector is aligned with the Positive subspace –in
which case, we can immediately see that we have to
be somewhat uncertain about Frequency.
We use two joint probability cases, namely, the
conjunction fallacy and the commutative property, to
illustrate how quantum probability is applied to our
operant conditioning vector space and how results
differ from a classical treatment.
Suppose that we ask first about frequency and
then whether the response applies the outcome, and
that we denote the answer to the first question as Fr
(a value between Reinforcement and Punishment)
and the answer to the second question as Ap (a value
between Positive and Negative). In quantum
probability theory, a conjunction of incompatible
questions involves projecting first to a subspace
corresponding to an answer for the first question
and, second, to a subspace for the second question
(Busemeyer, Pothos, Franco, and Trueblood, 2011).
The magnitude of a projection depends on the angle
between the corresponding subspaces. When the
angle between subspaces is large a lot of probability
amplitude is lost between successive projections. As
can be seen in Fig. 3, this can result in
||P
Ap
|Ψ||
2
< ||P
Ap
P
Fr
|Ψ||
2
,
that is, the direct projection to the Applies
subspace (blue line) is less than the projection to the
Applies subspace via the Frequency one (green line).
In classical terms, we have a situation whereby
Prob(Ap) < Prob(Ap & Fr),
which is impossible in classical probability
theory: The probability of two events occurring
together is always less than or equal to the
probability of either one occurring alone. The
opposite, assuming that specific conditions are more
probable than a single general one, is the well-
known conjunction fallacy.
The second case that illustrates that operant
conditioning may be governed by quantum
probabilities, refers to the effect of the order of the
observations. Consider the comparison between first
asking about Fr and then about Ap versus first
asking about Ap and then about Fr. By virtue of the
commutative property, in classical probability theory
the order of conjunction does not alter the result,
hence
Prob(Fr & Ap) = Prob(Ap & Fr).
However, in quantum probability theory P
A
P
B
P
B
P
A
, and thus, the conjunction of incompatible
questions fails commutativity. We see that
Prob(Fr & Ap) = ||P
Ap
P
Fr
|Ψ||
2
is larger than
Prob(Ap & Fr) = ||P
Fr
P
Ap
|Ψ||
2
because in the second case we project from |Ψ
to |Ap, losing a lot of amplitude (their relative angle
is large), and then from |Ap to |Fr we lose even
more amplitude.
In general, the smaller the angle between the
subspaces for two incompatible questions the greater
Posi ve
Nega ve
Ψ
(b)
ICAART2014-InternationalConferenceonAgentsandArtificialIntelligence
550

the relation between the answers. We lose little
amplitude by sequentially projecting the state vector
from one subspace to the other. That means that
accepting one answer makes the other very likely –
or, in classical terms, that they are highly correlated.
4 CONCLUSIONS
In this short paper we argue that quantum
probability might be a useful tool in representing
inherent uncertainty in observing (measuring)
behavioral states in operant conditioning and, by
extension, in reinforcement learning. Such states are
defined as the superposition of incompatible basis
vectors and thus cannot be represented using
classical probability –which axioms don’t apply. Our
approach, that borrows ideas from recent proposals
to use quantum probability in categorization (Pothos
& Busemeyer, 2009), addresses long-lasting calls to
formalize operant conditioning in a rigorous way
(e.g., Killeen, 1992). We have kept the formal
aspects of quantum probability to a minimum and
focused on illustrating with a simple example how
quantum probability principles can be used in
operant conditioning and why.
REFERENCES
Busemeyer, J. R., Pothos, E. M., Franco, R. & Trueblood,
J. S. (2011) A quantum theoretical explanation for
probability judgment errors. Psychological Review
118(2):193–218.
Domjan, M. (1994). Formulation of a behavior system for
sexual conditioning. Psychonomic Bulletin & Review,
1, 421-428.
Fanselow, M. S. (1994). Neural organization of the
defensive behavior system responsible for fear.
Psychonomic Bulletin & Review, 1, 429-438.
Hughes, R. I. G. (1989) The structure and interpretation of
quantum mechanics. Harvard University Press.
Isham, C. J. (1989) Lectures on quantum theory. World
Scientific.
Killeen, P. R. (1992). Mechanics of the animate. Journal
of the Experimental Analysis of Behavior, 57, 429-
463.
Kolmogorov, A. N. (1933/1950) Foundations of the theory
of probability. Chelsea Publishing Co.
Pothos, E. M. & Busemeyer, J. R. (2009) A quantum
probability explanation for violations of “rational”
decision theory. Proceedings of the Royal Society B
276:2171–78.
Skinner, B. F. (1938). The behavior of organisms: an
experimental analysis. Oxford, England: Appleton-
Century.
Staddon, J.E., & Cerutti, D. T. (2003). Operant behavior,
Annual Review of Psychology, vol. 54, 115-144.
Sutton, S. R., and Barto, A. G. (1998). Reinforcement
Learning: An Introduction. Cambridge, MA: MIT
Press.
Timberlake, W., & Silva, K. M. (1995). Appetitive
behavior in psychology, ethology, and behavior
systems. In N. Thompson (Ed.), Perspectives in
ethology: Vol. 11. Behavioral design, pp. 212-254.
NY: Plenum.
QuantumProbabilityinOperantConditioning-BehavioralUncertaintyinReinforcementLearning
551
