
Improving Kernel Grower Methods using Ellipsoidal Support Vector
Data Description
Sabra Hechmi, Alya Slimene and Ezzeddine Zagrouba
Higher Institute of Computer Science, Tunis El Manar University, 2 rue Abou Rayhane Bayrouni, 2080, Ariana, Tunisia
Keywords:
Kernel-based methods, Ellipsoidal Support Vector Data Description, Kernel Grower.
Abstract:
In these recent years, kernel methods have gained a considerable interest in many areas of machine learning.
This work investigates the ability of kernel clustering methods to deal with one of the meaningful problem of
computer vision namely image segmentation task. In this context, we propose a novel kernel method based
on an Ellipsoidal Support Vector Data Description ESVDD. Experiments conducted on a selected synthetic
data sets and on Berkeley image segmentation benchmark show that our approach significantly outperforms
state-of-the-art kernel methods.
1 INTRODUCTION
Segmentation is a low-level task of image processing.
It aims to partition an image into subsets called re-
gions according to some homogeneity criteria. Sev-
eral methods and techniques have been proposed for
image segmentation (Singh, 2010). However, the
choice of an appropriate method stays an open re-
search problem. In fact this depends on the nature
of the image and the domain application of segmen-
tation. Clustering methods like K-means and Fuzzy
K-means can be considered as a powerful tool used in
this context (Dehariya, 2010). Whereas, these algo-
rithms have been shown a good performance in clas-
sification of linear data, they are unable to generate
non-linear boundaries. Kernels give the possibility to
overcome this limitation.
The basic idea of kernel methods (Filippone,
2008) is to map data in the input space to a potentially
high dimensional feature space where a linear separa-
tion of data can be achieved. This is done through the
use of kernel function substituting the inner product
in the re-description space (Scholkopf, 2002). This
is known as Kernel Trick according to Reproduc-
ing Kernel Hilbert Spaces RKHS and Mercer’s Theo-
rem (Mercer, 1909). Among the most popular kernel
clustering methods include kernel k-means (Tzortzis,
2009) and kernel FCM (Kannan, 2011). Other class
of kernel clustering method includes methods based
on support vector data description SVDD (Tax, 2004)
like Kernel Grower KG (Camastra, 2005), scaled-up
KG (Chang, 2008) and at last PSO-based kernel clus-
tering method (Slimene, 2011). The main qualities of
referenced methods is their ability to extract arbitrar-
ily shaped clusters and their robustness against noises
and outliers.
In this paper, we propose a novel data descrip-
tion method called Ellipsoidal Support Vector Data
Description ESVDD based on the construction of
an hyper-ellipsoid around data instead of an hyper-
sphere in SVDD. The application of the proposed
method into a multi-class clustering context is also
investigated. The outline of this paper is as fol-
lows. Section 2 reviews related work. Section 3 dis-
cusses the proposed data description method. Section
4 presents the experimental results. Finally, Section 5
concludes the paper.
2 KERNEL CLUSTERING
METHODS
2.1 Kernels
A kernel is a similarity measure k between two points
x
i
and x
j
of an input set X, satisfying:
k : X ×X → R
k(x
i
, x
j
) =< φ(x
i
), φ(x
j
) > ∀x
i
, x
j
∈ X (1)
where φ is a mapping function that transforms X into
a high-dimensional feature space F (Mercer, 1909).
Kernels are employed to compute the dot product
343
Hechmi S., Slimene A. and Zagrouba E..
Improving Kernel Grower Methods using Ellipsoidal Support Vector Data Description.
DOI: 10.5220/0004923203430349
In Proceedings of the 3rd International Conference on Pattern Recognition Applications and Methods (ICPRAM-2014), pages 343-349
ISBN: 978-989-758-018-5
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

between data vectors in the feature space without
explicitly using φ(x
i
). So, any machine learning al-
gorithm that requires only the inner product between
data vectors, can be transformed into a kernel-based
algorithm.
There are many kernels but the most used are:
• Polynomial kernel of degree d:
k (a, b) = (< a, b > +c)
d
, f or c ≥ 0 (2)
• RBF kernel (or Gaussian kernel):
k (a, b) = e
−
ka−bk
2
2σ
2
(3)
2.2 Support Vector Data Description
and Scaled-up SVDD
2.2.1 Support Vector Data Description
SVDD is a one-class clustering method which con-
sist in constructing the optimal hyperplane with max-
imum margin separation between two classes. SVDD
aims at defining, in a feature space, a spherical shaped
description model (Tax, 2004) characterizing a closed
boundary around data set. This leads to the formu-
lation of a quadratic optimization problem defined as
follows:
min R
2
+C
n
∑
i=1
ξ
i
(4)
s.t k φ(x
i
) − a k
2
≤ R
2
+ ξ
i
, i = 1, ..., n , ξ
i
≥ 0
Where X = {x
1
, ..., x
n
} represents the set of data, a
and R are respectively the center and the radius of the
hyper-sphere, C is the trade off between margin and
excessive distances of outliers, φ is the mapping func-
tion and ξ
i
are slack variables introducing in order to
account for the excessive distance.
The above problem can be solved by optimizing
the following dual problem after introducing the La-
grange multipliers:
max
α
−
n
∑
i=1
n
∑
j=1
α
i
α
j
k(x
i
, x
j
) +
n
∑
i=1
α
i
k(x
i
, x
i
) (5)
Figure 1: The SVDD principle.
s.t 0 ≤ α
i
≤ C, i = 1, ..., n,
n
∑
i=1
α
i
= 1
α =
{
α
1
, ..., α
n
}
T
represents the dual variables’s set.
Generally, the Gaussian kernel is the most used kernel
function. Depending on the value of α
i
, data points
can be classified into targets (inside the sphere), out-
liers (outside the sphere) or support vectors (on the
boundary of the sphere) (Figure 1). Only data points
with non-zero α
i
are needed in the description of the
hyper-sphere, therefore they are called support vec-
tors. The SVDD has successfully employed in a
large variety of real-world applications such as pattern
denosing (Park, 2007), face recognition (Lee, 2006)
and anomaly detection (Banerjee, 2007). The main
drawback of SVDD is its computational complexity
due to the solving of quadratic optimization problem.
2.2.2 Scaled-up SVDD
This method was proposed (Chu, 2004) to improve
the scalability aspect of SVDD to deal with large scale
applications. In fact, SVDD can be viewed as a MEB
problem which is a geometric task that aims to find
the raduis and the center of the Minimum Enclosing
Ball of a set of objects in R
d
. Therefore, the scaled-up
SVDD is based on an approximation MEB algorithm
that employes the concept of core-sets (Kumar, 2003).
The scaled-up SVDD helps to reduce the optimiza-
tion problem complexity required by SVDD. This
makes SVDD problem handles large data sets with a
linear complexity in the number of data compared to
a cubic complexity in the original algorithm.
2.3 Kernel Grower and Scaled-up KG
2.3.1 Kernel Grower (KG)
Kernel Grower was proposed by Camastra and Verri
in 2005 (Camastra, 2005). It is based on K-means
algorithm in which the SVDD method is integrated.
However, and instead of computing the centers of
Figure 2: The inner circle presents the MEB of core set
(stars enclosed in squares) and its (1+ε) approximation con-
tains all stars.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
344

clusters, it computes the hyper-sphere enclosing the
data by means of the SVDD method.
Given a data set X = {x
1
, ..., x
n
}, where x
i
∈ R
d
.
Let k be a Gaussian kernel function with the associ-
ated feature map φ, z
i
= φ(x
i
) and
{
v
1
, ..., v
c
}
⊂ F is
the set of prototypes with c << n.
We define the Voronoi set Π
k
of v
k
as:
Π
k
(ρ) = {z
i
∈ F \k = argminkz
i
− v
k
k ≤ ρ} (6)
Where ρ > 0 is fixed by a model selection technique
(Bishop, 1995). So, KG is given as follows:
1: initialize c Voronoi sets Π
k
(ρ), k = 1, ..., c.
2: apply the SVDD for each Π
k
(ρ).
3: update each Π
k
(ρ).
4: stop if the Voronoi sets remain unchanged.
5: otherwise, return to step 2.
KG can generate nonlinear clustering bound-
aries, so it can give better classification results. But,
once this algorithm is based on SVDD method, it
suffers from his prohibitive O(n
3
) complexity which
stills expensive for use in applications requiring large
data sets.
2.4 Scaled-up KG
To overcome this default, Chang et al proposed a new
algorithm called scaled-up KG (Chang, 2008). This
method is a simple amelioration of KG which the
SVDD was replaced by the scaled-up SVDD to train
each Voronoi set. The main advantage of this im-
provement is the scalability to handle large data sets.
Therefore, this algorithm is successfully applied in
Berkely image segmentation and it gives interesting
results as a first step to allow kernel grower methods
to deal with large scale applications.
However, this method has two main problems:
first, the hyper-sphere can not always cover all target
data for all types of data sets, so it can include unnec-
essary data or space. Second, the important computa-
tional time that increases in terms of data number.
3 The Proposed Method
3.1 Ellipsoidal Support Vector Data
Description
In order to achieve a more flexible decision bound-
ary, we investigate to construct a description method
based on an hyper-ellipsoid shape model instead of an
hyper-sphere one. However this issue has been dis-
cussed in (Forghani, 2011), where it’s was assessed
that an hyper-ellipsoid based SVDD can describe data
better than an hyper-sphere based SVDD, the pro-
posed method of forghani has two drawbacks. Firstly,
the method fails to have a dual problem which is writ-
ten only in terms of α
i
. Secondly, the method can’t be
applied to large scale problem since it’s time consum-
ing. To address these problems, we propose a math-
ematical formulation of the hyper-ellipsoid SVDD
problem depending only of α
i
and which can be ap-
plied to large scale context.
Let us consider c
1
and c
2
two distinct points in R
d
.
We call ellipsoid with foci c
1
and c
2
, all points x sat-
isfying the following property:
kx − c
1
k + kx − c
2
k = d (7)
This means that the sum of distances from a point x
to the foci of the ellipsoid is constant and counting
the length of the major axis d.(Figure 3)
Figure 3: Parameters of the ellipsoid.
Therefore, the formulation of the hyper-ellipsoid of a
data set X={x
1
,...,x
n
} of n objects in a feature space
can be written as:
min d (8)
s.t kφ(x
i
) − c
1
k + kφ(x
i
) − c
2
k ≤ d ; i = 1, ..., n
To obtain a convex problem, we write it as:
min d
2
+C
n
∑
i=1
ξ
i
(9)
s.t (kφ(x
i
) − c
1
k + kφ(x
i
) − c
2
k)
2
≤ d
2
+ ξ
i
ξ
i
≥ 0
The Lagrangian L of the problem is:
L = d
2
+C
n
∑
i=1
ξ
i
+
n
∑
i=1
α
i
(kφ(x
i
)−c
1
k
2
+kφ(x
i
)−c
2
k
2
(10)
+2.kφ(x
i
) − c
1
k.kφ(x
i
) − c
2
k − d
2
− ξ
i
) −
n
∑
i=1
β
i
ξ
i
where α
i
≥ 0 et β
i
≥ 0 are the Lagrange multipliers.
L must be minimized with respect to d, c
1
, c
2
et ξ
i
and
maximized with respect to α
i
et β
i
.
ImprovingKernelGrowerMethodsusingEllipsoidalSupportVectorDataDescription
345

Setting partial derivatives to 0 and taking account of
new constraints, we obtain:
L = 4
n
∑
i=1
α
i
< φ(x
i
).φ(x
i
) > −4
n
∑
i=1
α
i
α
j
< φ(x
i
).φ(x
j
) >
(11)
Replace the dot products by the kernel function, we
get:
L = −4
n
∑
i=1
α
i
α
j
k(x
i
, x
j
) + 4
n
∑
i=1
α
i
k(x
i
, x
i
) (12)
s.t 0 ≤ α
i
≤ C i = 1, ..., n
n
∑
i=1
α
i
= 1
Solving the optimization problem described above,
gives rise to a set of values of α
i
, ∀i = 1...n satisfying
the following properties:
(kφ(x) − c
1
k + kφ(x) − c
2
k)
2
< d
2
⇒ α
i
= 0 (13)
(kφ(x) − c
1
k + kφ(x) − c
2
k)
2
= d
2
⇒ 0 < α
i
< C
(14)
(kφ(x) − c
1
k + kφ(x) − c
2
k)
2
> d
2
⇒ α
i
= C (15)
Indeed, the points value 0 ≤ α
i
≤ C are the support
vectors (SV ), but only points values 0 < α
i
< C are
located on the border of the ellipse (SV
<c
).
To judge an object z = φ(x) whether it is in the tar-
get class, its distance to the foci of ellipse is computed
and compared with d, if satisfies Eq. (23), it will be
accepted, and otherwise, rejected.
f (z) = (kz − c
1
k + kz − c
2
k)
2
≤ d
2
(16)
And since most of the α
i
are zero we find:
f (x) = 4k(x, x)+4
∑
SV
α
i
α
j
k(x
i
, x
j
)−8
∑
SV
α
i
k(x
i
, x) ≤ d
2
(17)
Finally, the value of the major axis d is given by:
d
2
= 4k(x
k
, x
k
) + 4
∑
SV
α
i
α
j
k(x
i
, x
j
) − 8
∑
sv
α
i
k(x
i
, x
k
)
(18)
where x
k
is a support vector (SV
<c
).
3.2 Generalized Sequential Minimum
Method GSMO
Since the formulation of an hyper-ellipsoid model
is a quadratic programming optimization problem,
then adopting algorithmic solutions to speed up the
method are needed. Such solutions include sequential
minimization optimization (SMO) (Platt, 1999)
which is a special algorithm that was developed
to solve quadratic optimization problems involved
in SVM formulation. Later, a generalized version
named GSMO (Keerthi, 2002) has been proposed to
solve any quadratic optimization problem written in
the form:
min f (α) =
1
2
α
T
Qα + p
T
α (19)
s.c a
i
≤ α
i
≤ b
i
,
∑
y
i
α
i
= c
where T note the transposed matrix Q positive semi-
definite matrix, a
i
≤ b
i
et y
i
6= 0 ∀i.
The meaningful idea of this algorithm that is
works in an iterative way is that at each iteration it op-
timizes the working set of four dual variables, keeps
all other variables fixed and continues with the rest of
the data.
3.3 Scaled-up ESVDD
Core-sets have played an important role to reduce the
time requirement in scaled-up SVDD . So we asked
the question whether the application of core-sets
remains valid in the case of hyper-ellipsoid. A
geometric problem known as MEE (Kumar, 2005)
seeking the Minimum Ellipsoid Enclosing a number
of points. Like the MEB problem, MEE is based on
the idea of core-sets to achieve an optimal solution
in terms of time. Therefore we have the idea to
use the core-sets concept to build an algorithm that
looks for a scaled-up Ellipsoidal Support Vector
Data Description or scaled-up ESVDD: For a set
S of N points, we fixed a random point x
0
of S.
Therefore, we seeked the n
0
closest points from x
0
and calculated their ESVDD that we noted MEE
1
.
For ε > 0, scaled-up ESVDD works as follows:
1: initialize S
1
= x
0
, d
1
the major axis of MEE
1
and
i = 1.
2: find the set of points P
i
that are located outside
(ε + 1) MEE
i
.
3: stop if | P
i
|≤ µN, the expected number of rejected
items.
4: otherwise, find z the closest point outside of
(ε + 1) MEE
i
, S
i+1
= S
i
+ z.
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
346

Figure 4: An example of the convergence procedure of the proposed method on Delta set. It takes 23 iterations to converge.
(a), (b), (c), (d), (e) and (f) present respectively the Initialization phase, Iteration 5, Iteration 10, Iteration 15, Iteration 20 and
finally, Itaration 23. All points are clustered into two classes with success at the last iteration.
5: find the new MEE(S
i+1
) and the value of its major
axis d
i+1
.
6: check if d
i+1
≥ (1 + cste.ε)d
i
.
7: increment i and return to the step 2.
3.4 Proposed Clustering Algorithm
Similar to the KG algorithm, the proposed algorithm
behaves as follows:
1: initialize c Voronoi sets Π
k
(ρ), k = 1, ..., c.
2: apply the scaled-up ESVDD for each Π
k
(ρ).
3: update each Π
k
(ρ).
4: stop if the Voronoi sets remain unchanged.
5: otherwise, return to step 2.
4 EXPERIMENTAL RESULTS
4.1 Synthetic and Real World Data Sets
In this section, we investigate the results of the pro-
posed algorithm on several artificial and publicly
available benchmark datasets, which are commonly
used in testing machine learning algorithms. We
choose as real world data set: Iris, Wisconsin and
Spam (Frank, 2010). Only Delta set (Mldata, 2009)
is used as a synthetic data set. The performance of
our algorithm is compared with previously presented
algorithms (KG and Scaled–up KG). We respect the
same evaluation conditions and the same results found
in (Chang, 2008). The comparison is done in terms of
CPU time and rate of correct classification.
In Table 1, T
1
presents the CPU time of KG, T
2
is
the CPU time of Scaled-up KG and T
4
is the CPU time
of the proposed method. ∗ means that the algorithm
needs too long time. We note that T
3
presents the
CPU of an interative algorithm similar to KG which
we tried to include the ESVDD proposed by Forghani
(Forghani, 2011) in a multi-class clustering problem.
This algorithm has a huge computational time noted
by (*) and hence can’t be applied to large scale clus-
tering problem. It can be seen that our method has
the lowest run time compared to other methods. Al-
though, it was noted that the number of iterations of
Table 1: Comparison in terms of CPU time.
Data set Data size T
1
T
2
T
3
T
4
Iris 150 12.94 47.95 * 10.6
Delta 424 226.28 9.39 * 8.23
Wisconsin 683 807.16 22.84 * 15.46
Spam 1534 * 44.82 * 22.48
Table 2: Comparison of average correct ratios.
Algorithm Iris Delta Wisconsin Spam
KG 94.7 100 97.0 81.3
Scaled up KG 93.4 100 96.8 80.2
our method 95.4 100 97.45 82.56
the proposed algorithm is slightly higher compared to
Scaled-up KG.
Table 2 illustrates the comparison results on av-
erage correct ratios of classification between KG,
scaled-up KG and our method. The results are sat-
isfactory and show that the improved method is able
to give a high clustering results on different types or
size of data. Indeed, the ellipsoidal boundary is effi-
cient and can generate non-linearly separable classes.
So, it is obvious that the effect of outliers is reduced.
4.2 Berkeley Image Segmentation
In this subsection, we use the Berkeley Segmentation
Data Set (Martin, 2001) to evaluate the performance
of our approach when it’s applied to a large scale con-
text and especially into the field of image segmenta-
tion. Berkeley Segmentation Data Set contains 300
images of natural scenes with at least one detectable
object in each image. The segmentation evaluation is
based on the Probabilistic Rand Index (PRI) (Unnikr-
ishnan, 2007). This index aims to compare between
a test segmentation and a multiple ground-truth im-
ages through a fraction of pairs of pixels whose la-
belling are consistent between the test segmentation
and the ground truth. Thereafter, an average is com-
ImprovingKernelGrowerMethodsusingEllipsoidalSupportVectorDataDescription
347
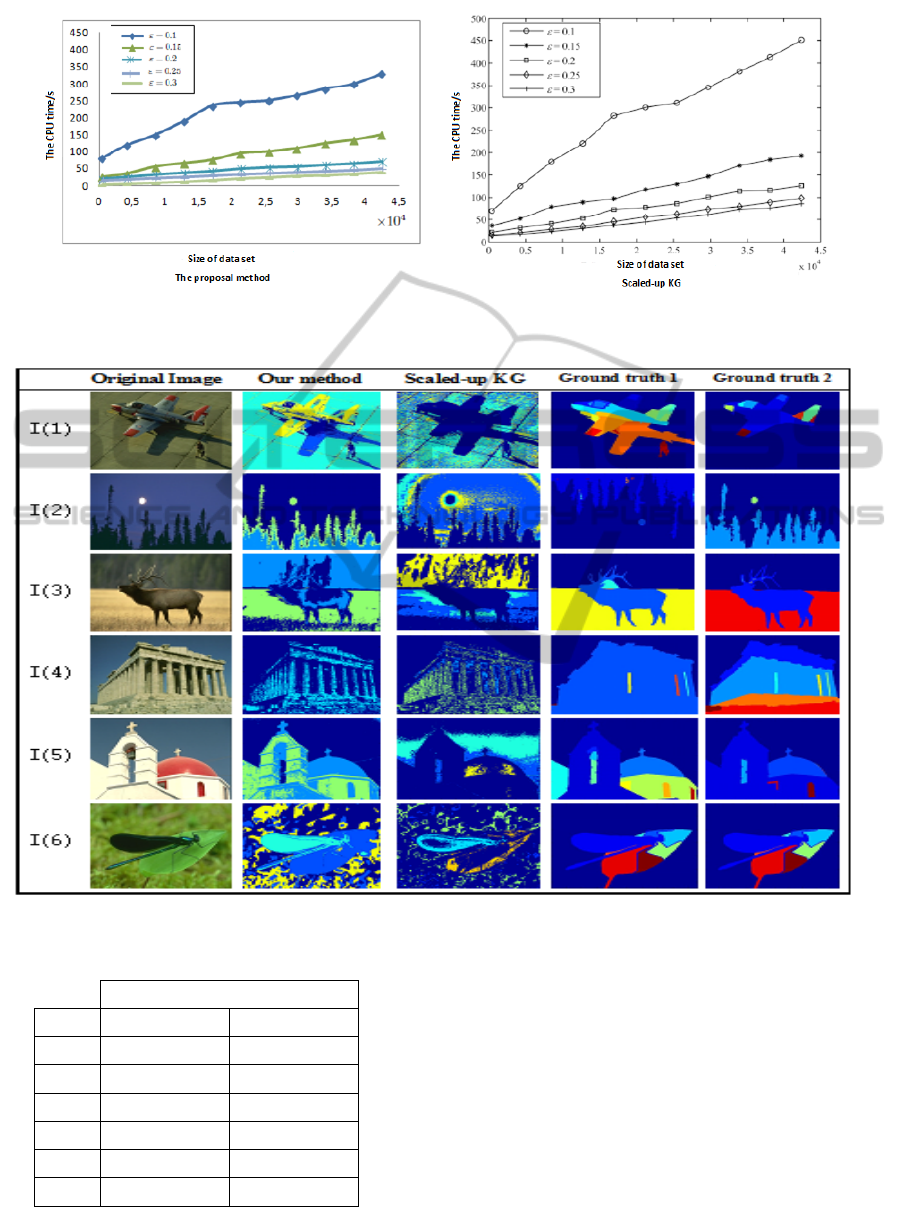
Figure 5: The two curves show the progressive appearance of CPU time for each algorithm according to the Delta set size
which the evolution accelerates linearly when ε increases. Our algorithm always displays the lowest CPU value.
Figure 6: Images segmented by the proposed method and scaled-up KG.
Table 3: PRI calculated for two algorithms.
Algorithm
Image Scaled-up KG Our algorithm
I(1) 0.464 0.584
I(2) 0.321 0.723
I(3) 0.412 0.593
I(4) 0.311 0.443
I(5) 0.560 0.610
I(6) 0.623 0.688
puted across all ground truth to account for scale vari-
ation in human perception. Figure 6 shows exam-
ples of image segmentation obtained by the proposed
method and the scaled-up KG. Also, we perform in
Table 3 a comparison between these two algorithms
in terms of PRI measurement. The results can attest
again the efficiency and performance of our classifi-
cation approach.
5 CONCLUSIONS
In this paper, we presented a novel kernel clustering
method that is based on an ellipsoidal support vec-
tor data description. In addition, we have proposed to
ICPRAM2014-InternationalConferenceonPatternRecognitionApplicationsandMethods
348

solve the optimizing problem with the GSMO algo-
rithm. Our method outperforms when compared with
other state-of-the art kernel clustering method. The
results are very encouraging and the proposed method
can be adapted to general clustering problems.
REFERENCES
Singh, K.K. and Singh, A. (2010). A Study of Image Seg-
mentation Algorithms for Different Types of Images.
In International Journal of Computer Science Issues,
vol. 7, no. 5.
Dehariya, V.K., Shrivastava, S.K. and Jain, R.C. (2010).
Clustering of Image Data Set Using K-Means and
Fuzzy K-Means Algorithms. In Computational Intel-
ligence and Communication Networks, pp. 386-391.
Filippone, M., Camastra, F., Masulli, F. and Rovetta, S.
(2008). A survey of kernel and spectral methods for
clustering. In Pattern Recognition, vol. 41, no. 1, pp.
176-190.
Schlkopf, B. and Smola, A.J. (2002). Learning with Ker-
nels. MIT Press Cambridge, MA, USA.
Mercer, J. (1909). Functions of positive and negative type
and their connection with the theory of integral equa-
tions. In Proceedings of the Royal Society of London,
vol. 83, no. 559, pp. 69-70.
Tzortzis, G.F. and Likas, A.C. (2009). The global kernel
k-means algorithm for clustering in feature space. In
IEEE Transactions on Neural Networks, vol. 20, no.
7, pp. 1181-1194.
Kannan, S.R., Ramathilagam, S., Devi, R. and Sathya, A.
(2011). Robust kernel FCM in segmentation of breast
medical images. In Expert Systems with Applications,
vol. 38, no. 4, pp. 4382-4389.
Tax, D.M.J. and Duin, R.P.W. (2004). Support vector data
description. In Machine Learning, vol. 54, no. 1, pp.
45-66.
Camastra, F. and Verri, A. (2005). A novel kernel method
for clustering. In IEEE transactions on Pattern Anal-
ysis and Machine Intelligence, vol. 27, no. 5, pp. 801-
805.
Chang, L., Deng, X.M., Zheng, S.W. and Wang, Y.Q.
(2008). Scaling up kernel grower clustering method
for large data sets via core-sets. In Acta Automatica
Sinica, vol. 34, no. 3, pp. 376-382.
Slimene, A. and Zagrouba, E. (2011). A new PSO based
kernel clustering method for image segmentation. In
SITIS, Signal Image Technology and Internet Based
Systems, pp. 350-357 .
Park, J., Kang, D., Kim, J., Kwok, J.T. and Tsang, I.W.
(2007). SVDD-Based Pattern Denoising. In Neural
Computation, vol. 19, no. 7, pp.1919-1938.
Lee, S.W. and Park, J. (2006). Low resolution face recog-
nition based on support vector data description. In
Pattern Recognition, vol. 39, no. 9, pp. 1809-1812.
Banerjee, A., Burlina, P. and Meth, R. (2007). Fast Hyper-
spectral Anomaly Detection via SVDD. In IEEE In-
ternational Conference on Image Processing, vol. 4,
pp. 101-104.
Chu, C.S., Tsang, I.W. and Kwok, J.T. (2004). Scaling up
support vector data description by using core-sets. In
IEEE International Joint Conference on Neural Net-
works, vol. 1, pp. 425-430.
Kumar, P., Mitchell, J.S.B. and Yildirim, E.A. (2003). Ap-
proximate Minimum Enclosing Balls in High Dimen-
sions Using Core-Sets. In Experimental Algorithmics,
vol.8, no.1, pp. 1.
Bishop, C. (1995). Neural Networks for Pattern Recogni-
tion. Oxford University Press, USA.
Forghani, Y., Effati, S., Yazdi, H.S. and Tabrizi, R.S. (2011).
Support vector data description by using hyper-ellipse
instead of hyper-sphere. In International Conference
on Computer and Knowledge Engineering, pp. 22-27.
Platt, J.C., (1999). Fast training of support vector machines
using sequential minimal optimization. In Advances
in Kernel Methods: Support Vector Learning, pp. 185-
208.
Keerthi, S.S. (2002). Convergence of a Generalized SMO
Algorithm for SVM Classifier Design. In Machine
Learning, vol. 46, pp. 351-360.
Kumar, P. and Yildirim, E.A. (2005). Minimum-Volume
Enclosing Ellipsoids and Core Sets. In Optimization
theory and applications, vol. 126, no. 1, pp. 1-21.
Frank, A. and Asuncion, A. (2010).
Mldata, Machine Learning Data set Repository. (2009).
Martin, D., Fowlkes, C., Tal, D. and Malik, J. (2001).
A Database of Human Segmented Natural Images
and Its Application to Evaluating Segmentation Algo-
rithms and Measuring Ecological Statistics.
Unnikrishnan, R., Pantofaru, C. and Hebert, M. (2007). To-
ward objective evaluation of image segmentation al-
gorithms. IEEE Transactions on pattern analysis and
machine intelligence, vol. 29, no. 6, pp. 929-944.
ImprovingKernelGrowerMethodsusingEllipsoidalSupportVectorDataDescription
349
