Cost-efficient Capacitation of Cloud Data Centers for QoS-aware
Multimedia Service Provision
Ronny Hans
1
, Ulrich Lampe
1
, Michael Pauly
2
and Ralf Steinmetz
1
1
Multimedia Communications Lab (KOM), TU Darmstadt, Rundeturmstr. 10, 64283 Darmstadt, Germany
2
T-Systems International GmbH, Pascalstr. 51, 52076 Aachen, Germany
Keywords:
Cloud Computing, Data Center, Capacitation, Quality of Service, Multimedia, Service.
Abstract:
Cloud infrastructure is increasingly used for the provision of sophisticated multimedia services, such as cloud
gaming or Desktop as a Service, with stringent Quality of Service demands. Serving these service demands
results in the need to cost-efficiently select and capacitate data centers. In the work at hand, we introduce the
corresponding Cloud Data Center Capacitation Problem and propose two optimization approaches. Through
a quantitative evaluation, we demonstrate that an exact solution approach is only practically applicable to
small problem instances, whereas a heuristic based on Linear Program relaxation achieves significant reduc-
tions in computation time of about 80% while retaining a favorable solution quality, with cost increases of
approximately 5% or less.
1 INTRODUCTION
Since the term was first coined in the mid-2000s,
cloud computing has received increasing attention by
both IT practitioners and researchers. In this con-
text, a focus has often been on Infrastructure as a
Service, given that it is the most flexible among the
three cloud computing service models (Briscoe and
Marinos, 2009) and that its successful application has
been widely documented in the literature, e. g., (Arm-
brust et al., 2009). However, with the increasing ma-
turity of cloud computing, the focus is shifting toward
the cloud-based delivery of sophisticated multimedia
services. Such software-oriented services include, for
example, cloud gaming / Games as a Service (Chang,
2010) or Dekstop as a Service (Erdogmus, 2009).
Due to their nature, such multimedia services pose
high demands concerning Quality of Service (QoS)
attributes. Unfortunately, past empirical research has
shown that the current cloud infrastructure is partially
insufficient to meet those demands, most notably due
to the latency that arises from the massive centraliza-
tion of cloud data centers in few geographical loca-
tions (Choy et al., 2012).
Accordingly, in the work at hand, we examine
how cloud data centers can be appropriately selected
and capacitated in order to serve QoS-aware multime-
dia services. In our previous work (Hans et al., 2013),
we have addressed the selection of cloud data centers
for single service types and time-invariant service de-
mands. The work at hand expands our past research
through the consideration of multiple service types, as
well as fluctuating service demands, and also regards
the resulting distinction between variable costs for op-
eration and reservation of cloud infrastructure. In this
context, we propose an exact solution approach, based
on an Integer Program (IP) formulation, as well as a
heuristic approach based on Linear Program (LP) re-
laxation.
The remainder of this paper is structured as fol-
lows: In Section 2, we briefly explain the specific
problem that is addressed in this paper. In Sec-
tion 3, we introduce formal notations, based on which
we specify two optimization approaches. These ap-
proaches are quantitatively evaluated in Section 4. An
overview of related work is given in Section 5. Sec-
tion 6 concludes the paper with a brief summary and
outlook on future work.
2 PROBLEM STATEMENT
In this work, we assume the role of a service provider,
who aims to deliver multimedia services to a dis-
tributed set of users. Specifically, we consider a set
of so-called user clusters, each of which represents
a predefined number of users in a certain geographi-
158
Hans R., Lampe U., Pauly M. and Steinmetz R..
Cost-efficient Capacitation of Cloud Data Centers for QoS-aware Multimedia Service Provision.
DOI: 10.5220/0004947101580163
In Proceedings of the 4th International Conference on Cloud Computing and Services Science (CLOSER-2014), pages 158-163
ISBN: 978-989-758-019-2
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

cal location, e. g., a state or county. Each user cluster
exhibits specific demands for a given set of service
types, with the demand fluctuating over a predefined
number of time slots. If these demands cannot be
met, certain penalties accrue. Furthermore, each ser-
vice type is associated with certain QoS requirements,
e. g., concerning permissible latency.
In order to deliver his/her services, the provider
has the choice among a given set of data centers. The
selection of a data center incurs certain fixed costs,
e. g., for construction or long-term lease. In addition,
the operation of a server within each data center re-
sults in certain variable costs. Furthermore, the reser-
vation of a number of servers over the planning period
may incur certain variable reservation costs. Due to
the geographical distribution, each data center makes
different QoS guarantees with respect to each user
cluster.
The aim of the provider is to choose among the
data centers and further take a capacitation decision,
i. e., decide on the number of reserved servers, such
that the overall cost of the solution is minimized. In
the following, we refer to this problem – which is a
generalization of a research issue we previously ex-
amined (Hans et al., 2013) – as Cloud Data Center
Capacitation Problem (CDCCP).
3 OPTIMIZATION APPROACHES
In the following, we first introduce a set of nota-
tions to formally represent the CDCCP (cf. Sec-
tion 3.1). Subsequently, we introduce two optimzi-
ation approaches, namely an exact approach based on
Integer Programming (cf. Section 3.2) and a heuristic
approach based on LP relaxation (cf. Section 3.3).
3.1 Formal Notations
In order to represent the CDCCP in the form of a
mathematical model, a few formal notations are re-
quired. To begin with, we formally define the basic
entities within the CDCCP using the following sym-
bols:
• D = {1, 2, ..., D
#
}: Set of (potential or existing)
data centers
• U = {1, 2, ..., U
#
}: Set of user clusters
• S = {1, 2, ..., S
#
}: Set of available services
• Q = {1, 2, ..., Q
#
}: Set of considered QoS at-
tributes
• T = {1, 2, ..., T
#
}: Set of discrete time slots within
the planning period
Based on the previously introduced basic entities, the
parameters that are associated with the individual en-
tities can be defined as follows:
• SD
u,s,t
: Service demand of user u for service s at
time t
• K
min
d
∈ R: Minimal capacity of data center d
• K
max
d
∈ R: Maximal capacity of data center d
• CF
d
∈ R: Fixed cost of selecting data center d
• CVO
d
∈ R: Variable cost for operating one server
unit for one time unit in data center d
• CVR
d
∈ R: Variable cost for reserving one server
unit in data center d
• CP
u,s
∈ R: Penalty cost per service unit not pro-
vided to user u w.r.t. service s
• QG
d,u,q
∈ R: QoS guarantee of data center d w.r.t.
user u for QoS attribute q
• QR
u,s,q
∈ R: QoS requirement of user u w.r.t. ser-
vice s for QoS attribute q
Lastly, in order to model the CDCCP as optimization
problem, we use the following decision variables:
• x
d
: Selection of a data center d
• y
d,u,s,t
: Capacity provided by data center d to user
cluster u concerning service s at time t
• y
0
u,s,t
: Penalty-bound capacity not provided to user
cluster u concerning service s at time t
• z
d
: Capacity reserved in data center d
3.2 Exact Optimization Approach
CDCCP-EXA.KOM
Based on the notations from the previous section, the
CDCCP can be modeled as an optimization prob-
lem in an intuitive manner. The result is provided in
Model 1 and will be explained in detail in the fol-
lowing. To begin with, Equation 1 defines the objec-
tive function, aiming at a minimization of total costs,
depending on the values of the decision variables.
Equation 2 ensures that all service demands will be
satisfied or that corresponding penalties will accrue.
Equation 3 links the decision variables y and z, ensur-
ing that only the reserved capacity in each data center
may be used in each time slot. Equations 4 and 5
make sure that the capacity constraints for each data
center are held. Equation 6 ensures that the QoS re-
quirements of each user cluster are matched by the
corresponding data center guarantees, depending on
the value of the auxiliary variable p from Equation 7.
Lastly, Equation 8 defines the decision variables as
binary and natural.
Cost-efficientCapacitationofCloudDataCentersforQoS-awareMultimediaServiceProvision
159

As can easily be seen, Model 1 constitutes an IP.
Such problems can be solved using off-the-shelf al-
gorithms, most notably the branch-and-bound algo-
rithm (Domschke and Drexl, 2004). However, despite
its efficiency in many application scenarios, branch-
and-bound is based on the principle of enumeration
(Hillier and Lieberman, 2005). Hence, in the worst
case, the time complexity of computing a solution to
a given problem instance grows exponentially with
the number of decision variables, i. e., the number
of entities in the model. Accordingly, the practical
applicability of CDCCP-EXA.KOM is likely limited
to smaller problem instances and situations where the
computation time requirements play an inferior role.
3.3 Heuristic Optimization Approach
CDCCP-REL.KOM
The brief qualitative analysis from the previous sec-
tion indicates a potentially high computational com-
plexity for the exact approach CDCCP-EXA.KOM.
Based on this notion, we introduce a heuristic ap-
proach that is based on the common concept of LP
relaxation (Domschke and Drexl, 2004). Specifically,
the binary and integer decision variables in the initial
model (cf. Equation 8) are substituted by correspond-
ing natural variables (cf. Equation 9).
The resulting LP formulation of the initial prob-
lem can be solved using another set of off-the-shelf
algorithms, such as interior point methods. In contrast
to branch-and-bound, such algorithms are character-
ized by polynomial, rather than exponential worst
case time complexity (Hillier and Lieberman, 2005).
This renders them potentially applicable to larger
problem instances, even under relatively rigid time
constraints. From the LP-based solution, a final so-
lution can simply be deduced by rounding all natural
values of the decision variables to the next-highest in-
teger.
4 EVALUATION
4.1 Setup
In order to assess the applicability of our proposed
optimization approaches, we prototypically imple-
mented them in Java 7. As solver framework, we
used IBM ILOG CPLEX 12.5
1
, which was accessed
through the JavaILP middleware
2
.
1
http://www.ibm.com/software/integration/optimization
/cplex-optimizer/
2
http://javailp.sourceforge.net/
Model 1. Cloud Data Center Capacitation Problem.
Min. C(x, y, z) =
∑
d∈D
x
d
×CF
d
(1)
+
∑
d∈D,u∈U,s∈S,t∈T
y
d,u,s,t
×CVO
d
+
∑
d∈D,u∈U,s∈S,t∈T
y
0
u,s,t
× ×CP
u,s
+
∑
d∈D
z
d
×CV R
d
y
0
u,s,t
+
∑
d∈D
y
d,u,s,t
≥ SD
u,s,t
(2)
∀u ∈ U, ∀s ∈ S, ∀t ∈ T
∑
u∈U,s∈S
y
d,u,s,t
≤ z
d
∀d ∈ D, ∀t ∈ T (3)
z
d
≤ x
d
× K
max
d
∀d ∈ D (4)
z
d
≥ x
d
× K
min
d
∀d ∈ D (5)
y
d,u,s,t
≤ p
d,u,s
× K
max
d
(6)
∀d ∈ D, ∀u ∈ U, ∀s ∈ S, ∀t ∈ T
p
d,u,s
=
(
1 if QG
d,u,q
≤ QR
u,s,q
∀q ∈ Q
0 else
(7)
x
d
∈ {0, 1} ∀d ∈ D (8)
y
d,u,s,t
∈ N ∀d ∈ D, ∀u ∈ U, ∀s ∈ S, ∀t ∈ T
y
0
u,s,t
∈ N ∀u ∈ U, ∀s ∈ S, ∀t ∈ T
z
d
∈ N ∀d ∈ D
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
x
d
∈ R, 0 ≤ x
d
≤ 1 ∀d ∈ D
y
d,u,s,t
∈ R, y
d,u,s,t
≥ 0 ∀d ∈ D, ∀u ∈ U, ∀s ∈ S, ∀t ∈ T
y
0
u,s,t
∈ R, y
u,s,t
≥ 0 ∀∀u ∈ U, ∀s ∈ S, ∀t ∈ T
z
d
∈ R, z
d
≥ 0 ∀d ∈ D
(9)
In accordance with Silver (Silver, 2004), our eval-
uation focuses on two dependent variables, namely
computation time and solution quality (i. e., total cost
associated with the computed solution). As indepen-
dent variables, we considered the number of data cen-
CLOSER2014-4thInternationalConferenceonCloudComputingandServicesScience
160

ters (D
#
), user clusters (U
#
), service types (S
#
), and
time slots (T
#
), since they have a direct impact on the
number of decision variables, and hence, the size of
the solution space. We used a fractional factorial de-
sign, varying the value of each independent variable
separately while treating the remaining variables as
controlled, i. e., assuming a fixed value.
In accordance with our previous work (Hans et al.,
2013), we employed data from the 2010 United States
census
3
as the basis for problem generation. In or-
der to model data centers and user clusters, we ran-
domly drew US counties from the census data, and
set the service demands and different cost parameters
based on the according county population and median
income. As the only QoS requirement, we consid-
ered latency and set it to represent different multi-
media service types, ranging from cloud gaming to
Desktop as a Service. The QoS guarantees were fi-
nally computed based on the geographical distance
between data centers and user clusters.
For each test case, i. e., distinct combination of
values for the independent variables, we randomly
created 50 problem instances. Problems that could
not be successfully solved by the heuristic approach
CDCSP-REL.KOM were removed from the sample;
such invalid solutions may result from certain capac-
ity constraints not being met due our simplistic next-
highest integer rounding approach (cf. Section 3.3).
Based on the samples, we subsequently computed the
observed mean absolute computation times, as well
as the macro-averaged ratios of computation time and
total cost between CDCCP-REL.KOM and CDCCP-
EXA.KOM, along with the respective 95% confi-
dence intervals based on a t-distribution (Kirk, 2007).
The evaluation was conducted on a desktop computer,
equipped with an Intel Core 2 Quad Q9450 processor
and 4 GB of memory, operating under Microsoft Win-
dows 7.
4.2 Results and Discussion
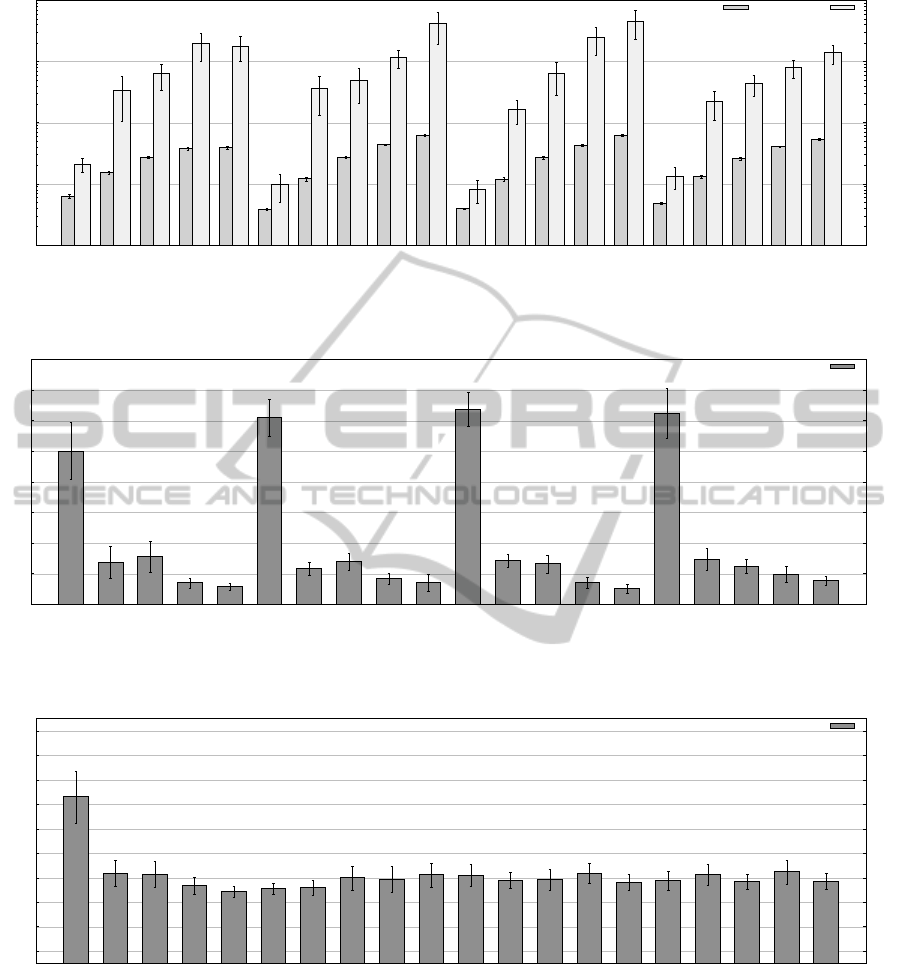
The results of our evaluation are presented in Fig-
ures 1 through 3. As can be seen in Figure 1, the
observed mean absolute computation times strikingly
confirm the different computational complexity of
CDCCP-EXA.KOM and CDCCP-REL.KOM. Even
for the smallest considered test cases, the computa-
tion time for CDCCP-EXA.KOM ranges in the order
of magnitude of 1 s, quickly growing to 10 s or even
100 s with an increasing size of the problem instances.
In contrast, the mean computation times for CDCCP-
REL.KOM remain in the order of magnitude of 10 s,
3
http://www.census.gov/geo/maps-data/data/gazetteer
.html
even for the largest problem classes. These find-
ings are also confirmed by the macro-averaged ratios
of computation times, as given in Figure 2. Except
for the smallest problem classes, CDCCP-REL.KOM
consistently reduces the computation time by about
80% or more to CDCCP-EXA.KOM. The reduction
is statistically significant across all test cases at the
assumed confidence level of 95% (i. e., α = 0.05).
On the downside, Figure 3 indicates that the appli-
cation of LP relaxation in CDCCP-REL.KOM comes
at a certain amount of additional cost, i. e., degra-
dation in solution quality. Compared to CDCCP-
EXA.KOM, the increase ranges between approxi-
mately 0.4% and 4.3%; however, it does not exceed
1.5% for all considered test cases except one. Thus,
while the slight increase is statistically significant for
practically all test cases at the 95% confidence level,
it can be considered quite marginal and most likely
acceptable in practical applications. In addition, as
can be seen from the given sample sizes, CDCCP-
REL.KOM is able to provide valid solutions to essen-
tially all considered problem instances, except in six
test cases, where one instance respectively could not
be solved.
In conclusion, we find that the exact optimiza-
tion approach CDCCP-EXA.KOM is associated with
high computational complexity and hence, its practi-
cal application is limited to small problem instances.
However, the approach can also serve as a benchmark
for the assessment of alternative solution approaches,
such as CDCCP-REL.KOM. The latter has presented
a much more favorable performance in our experi-
ments with respect to computational demands. Never-
theless, the development of custom-tailored optimiza-
tion approaches for the CDCCP that do not rely on LP
formulations may provide further improvements con-
cerning the trade-off between computational require-
ments and solution quality.
5 RELATED WORK
In recent years, there has been vivid research in the
area of cloud computing. In the following, we briefly
discuss selected works that are most closely related to
our research.
(Goiri et al., 2011) present an approach for effi-
cient data center placement based on several factors,
e. g., available network backbones and proximity of
population centers. To find a solution for the place-
ment problem, the authors use a combination of ex-
act and approximate approaches. Thereby, Goiri et al.
focus on design time, i. e., construction planning for
new data centers. In contrast to our work, they do not
Cost-efficientCapacitationofCloudDataCentersforQoS-awareMultimediaServiceProvision
161

0.1
1
10
100
1000
D
#
= 5
(50)
D
#
= 10
(50)
D
#
= 15
(50)
D
#
= 20
(49)
D
#
= 25
(50)
U
#
= 25
(50)
U
#
= 50
(49)
U
#
= 75
(49)
U
#
= 100
(50)
U
#
= 125
(50)
S
#
= 1
(50)
S
#
= 2
(50)
S
#
= 3
(49)
S
#
= 4
(50)
S
#
= 5
(49)
T
#
= 3
(50)
T
#
= 6
(49)
T
#
= 9
(50)
T
#
= 12
(50)
T
#
= 15
(50)
Mean Computation Time [s]
Test Case (Sample Size)
CDCCP-REL.KOM CDCCP-EXA.KOM
Figure 1: Observed mean computation times (with 95% confidence intervals) by test case. Please note the logarithmic scaling
of the ordinate. If not specified differently, we use D
#
= 15, U
#
= 75, S
#
= 3, and T
#
= 9 for the independent variables.
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
D
#
= 5
(50)
D
#
= 10
(50)
D
#
= 15
(50)
D
#
= 20
(49)
D
#
= 25
(50)
U
#
= 25
(50)
U
#
= 50
(49)
U
#
= 75
(49)
U
#
= 100
(50)
U
#
= 125
(50)
S
#
= 1
(50)
S
#
= 2
(50)
S
#
= 3
(49)
S
#
= 4
(50)
S
#
= 5
(49)
T
#
= 3
(50)
T
#
= 6
(49)
T
#
= 9
(50)
T
#
= 12
(50)
T
#
= 15
(50)
Ratio of Computation Time
Test Case (Sample Size)
CDCCP-REL.KOM / CDCCP-EXA.KOM
Figure 2: Ratio of computation times (based on macro-average; with 95% confidence intervals) between the two optimization
approaches by test case. Configuration identical to Figure 1.
0.98
0.99
1
1.01
1.02
1.03
1.04
1.05
1.06
1.07
D
#
= 5
(50)
D
#
= 10
(50)
D
#
= 15
(50)
D
#
= 20
(49)
D
#
= 25
(50)
U
#
= 25
(50)
U
#
= 50
(49)
U
#
= 75
(49)
U
#
= 100
(50)
U
#
= 125
(50)
S
#
= 1
(50)
S
#
= 2
(50)
S
#
= 3
(49)
S
#
= 4
(50)
S
#
= 5
(49)
T
#
= 3
(50)
T
#
= 6
(49)
T
#
= 9
(50)
T
#
= 12
(50)
T
#
= 15
(50)
Ratio of Cost
Test Case (Sample Size)
CDCCP-REL.KOM / CDCCP-EXA.KOM
Figure 3: Ratio of costs (based on macro-average; with 95% confidence intervals) between the two optimization approaches
by test case. Configuration identical to Figure 1.
consider time-variant service demands.
(Choy et al., 2012) study the current cloud infras-
tructure with respect to cloud gaming. The authors
demonstrate that the current Amazon EC2 data cen-
ters could only serve 70% of the US population with
adequate latency. Based on this finding, they propose
the use of so-called edge servers to extend the current
existing infrastructure, and validate their proposal us-
ing simulation approaches. In contrast to us, Choy et
al. do not propose an exact approach for data center
capacitation, and do not consider time-variant service
demand.
(Larumbe and Sans
`
o, 2012) present an optimiza-
tion approach that addresses three distinct, yet inter-
CLOSER2014-4thInternationalConferenceonCloudComputingandServicesScience
162

linked problems: the geographical location of data
centers, the location of software components that are
hosted in network nodes and routing. Because the au-
thors see a close connection between these problems,
they integrated them in one mathematical framework
using an optimal approach. Similar to the two afore-
mentioned papers, this work only considers static ser-
vice demand. Also, it exclusively provides an exact,
but not a heuristic solution approach.
In summary, to the best of our knowledge, our
work is the first to address the cost-efficient capaci-
tation and placement of cloud data centers for QoS-
aware services under consideration of time-variant
service demand. In this context, this paper not
only provides the exact solution approach CDCCP-
EXA.KOM but also an initial heuristic solution,
CDCCP-REL.KOM, which features substantially re-
duced computation times.
6 SUMMARY AND OUTLOOK
Cloud-based delivery of multimedia services, such as
cloud gaming or Desktop as a Service, offers great
economic potential. However, the adequate design
of the underlying cloud infrastructure is a challeng-
ing task that has been only insufficiently addressed
in research so far. In this work, we introduced the
according Cloud Data Center Capacitation Problem
(CDCCP). We proposed an exact solution approach,
named CDCCP-EXA.KOM, based on Integer Pro-
gramming. We further proposed a basic heuristic,
called CDCCP-REL.KOM, which is based on the
principle of Linear Program relaxation. Based on
a quantitative evaluation, we showed that CDCCP-
EXA.KOM is only practically applicable to smaller
problem instances due to its exponential computa-
tional complexity. In contrast, CDCCP-REL.KOM
features polynomial time complexity, thus signifi-
cantly reducing the required computational effort for
solving individual problem instances by 80% or more.
At the same time, the heuristic maintains a favor-
able solution quality, with cost increases generally
amounting to less than 5% compared to an exact so-
lution.
Our future work primarily aims at the develop-
ment of further heuristic approaches, which provide
an even more favorable tradeoff between computa-
tional complexity and solution quality. Furthermore,
we will extend the proposed approaches to account for
stochastic, rather than just deterministic parameters,
e. g., uncertain service demands or QoS properties.
ACKNOWLEDGEMENTS
This work has partly been sponsored by the E-Finance
Lab e.V., Frankfurt a.M., Germany and by the Ger-
man Research Foundation (DFG) in the CRC 1053 –
MAKI.
REFERENCES
Armbrust, M., Fox, A., Griffith, R., Joseph, A., Katz, R.,
Konwinski, A., Lee, H., Patterson, D., Rabkin, A.,
Stoica, I., et al. (2009). Above the Clouds: A Berke-
ley View of Cloud Computing (TR UCB/EECS-2009-
28). Technical report, UC Berkeley.
Briscoe, G. and Marinos, A. (2009). Digital Ecosystems in
the Clouds: Towards Community Cloud Computing.
In DEST 2009.
Chang, T. (2010). Gaming Will Save Us All. Communica-
tions of the ACM, 53(3):22–24.
Choy, S., Wong, B., Simon, G., and Rosenberg, C. (2012).
The Brewing Storm in Cloud Gaming: A Measure-
ment Study on Cloud to End-User Latency. In
NetGames 2012.
Domschke, W. and Drexl, A. (2004). Einf
¨
uhrung in Opera-
tions Research. Springer, 6th edition. In German.
Erdogmus, H. (2009). Cloud Computing: Does Nirvana
Hide Behind the Nebula? IEEE Software, 26(2):4–6.
Goiri, I., Le, K., Guitart, J., Torres, J., and Bianchini, R.
(2011). Intelligent Placement of Datacenters for In-
ternet Services. In ICDCS 2011.
Hans, R., Lampe, U., and Steinmetz, R. (2013). QoS-
Aware, Cost-Efficient Selection of Cloud Data Cen-
ters. In CLOUD 2013.
Hillier, F. and Lieberman, G. (2005). Introduction to Oper-
ations Research. McGraw-Hill, 8th edition.
Kirk, R. (2007). Statistics: An Introduction. Wadsworth
Publishing, 5th edition.
Larumbe, F. and Sans
`
o, B. (2012). Optimal Location
of Data Centers and Software Components in Cloud
Computing Network Design. In CCGRID 2012.
Silver, E. (2004). An Overview of Heuristic Solution
Methods. J. of the Operational Research Society,
55(9):936–956.
Cost-efficientCapacitationofCloudDataCentersforQoS-awareMultimediaServiceProvision
163