Using Technology to Accelerate the Construction of Concept

Inventories

Latent Semantic Analysis and the Biology Concept Inventory

Kathy Garvin-Doxas

, Michael Klymkowsky

, Isidoros Doxas

and Walter Kintsch

Center for Integrated Plasma Studies, University of Colorado, Boulder, CO, U.S.A.

(Present address: Boulder Internet Technologies, Columbia, MD, U.S.A.)

Department of Molecular, Cellular and Developmental Biology, University of Colorado, Boulder, CO, U.S.A.

Center for Integrated Plasma Studies, University of Colorado, Boulder, CO, U.S.A.

(Present address: BAE Systems, Columbia, MD, U.S.A.)

Institute of Cognitive Science, University of Colorado, Boulder, CO, U.S.A.

Keywords: Concept Inventory, Biology Concept Inventory, Misconceptions, Latent Semantic Analysis.

Abstract: Concept Inventories are multiple choice instruments that map students’ conceptual understanding in a given

subject area. They underpin some of the most effective teaching methods in science education, but they are

labour intensive and expensive to construct, which limits their wide use in instruction. We describe how we

use Latent Semantic Analysis to accelerate the construction of Concept Inventories in general, and the

Biology Concept Inventory in particular.

1 INTRODUCTION

Concept Inventories are multiple choice instruments

that explore students’ conceptual understanding in a

given subject area. To accomplish this, CI

developers look for verbal markers that can be used

as proxies for identifying students’ conceptual

structures, much as we try to find DNA markers for

various traits. Well constructed CIs provide

researchers with a map of the students’ conceptual

landscape, which can be used to inform instruction

in that area.

Research-based teaching methods that are firmly

based on misconception research and make

consistent use of collaborative learning are the most

widely used national-scale tested methods that

consistently produce learning gains significantly

superior to lectures in Physics and Astronomy (eg.

McDermott et al., 1998; Zeilik et al., 1997; Hake

1998). Short of one-on-one tutoring (cf. Bloom’s

“two sigma challenge”, Bloom, 1984), this is the

best model available for impacting student learning.

Although consistently successful, the model also

incorporates a significant barrier to its wide

adoption, replicability, and extensibility. It is

critically dependent on the existence of well-

researched assessment instruments that can reliably

diagnose a student’s misconceptions, and which

require considerable time and effort to produce.

Although several groups, both academic and

commercial are currently engaged in developing

such instruments in disciplines such as biology (e.g.

Garvin-Doxas and Klymkowsky, 2008; Smith et. al.,

2008; Kalas et. al. 2013), geoscience (e.g. Libarkin

and Anderson, 2006), and engineering (e.g. Midkiff

et. al., 2001), no substantial advance has been made

in the time, effort, and expense required to develop a

validated, reliable instrument.

Here we describe the construction of Concept

Inventories and how it differs from the construction

of tests, and we show how we use Latent Semantic

Analysis (LSA, Landauer et. al., 1998; Landauer and

Dumais, 1997) to facilitate the usually labour

intensive validation phase of Concept Inventories in

general, and the Biology Concept Inventory (Garvin-

Doxas and Klymkowsky, 2008; Klymkowsky and

Garvin-Doxas, 2008) in particular.

301

Garvin-Doxas K., Klymkowsky M., Doxas I. and Kintsch W..

Using Technology to Accelerate the Construction of Concept Inventories - Latent Semantic Analysis and the Biology Concept Inventory.

DOI: 10.5220/0004957403010308

In Proceedings of the 6th International Conference on Computer Supported Education (CSEDU-2014), pages 301-308

ISBN: 978-989-758-021-5

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

2 CONCEPT INVENTORIES

AND TESTS

Although CIs bear a strong resemblance to

standardized tests, the two types of instruments are

very different, having fundamentally different aims.

Tests are basically designed to answer the question

“what percentage of the desired knowledge and

skills in this field has this student acquired?”. CIs

are meant to answer the question “what conceptual

constructs is this student using when solving

problems in this field?”. These same questions can

also be asked from the point of view of an ensemble

of students (rather than the individual student). From

that point of view tests are meant to rank the

students in the ensemble according to their skill and

knowledge, while CIs are meant to report the

percentage of students in the ensemble that use a

particular conceptual construct.

The two descriptions (individual and ensemble)

must of course be equivalent, since they are both

describing the same underlying system. This is

harder than it sounds, and it is the source of most

difficulties, both practical and conceptual, in all

statistical descriptions of systems from Physics to

Economics. What that means, is that for any given

case we should come up with the exact same

observable answers whether we are looking at the

individual view (eg. calculating the likely trajectory

of an electron hole in a semiconductor, or the likely

portfolio value of an individual investor) or the

ensemble view (ie. calculating the total current in the

semiconductor, or the total retirement savings of a

population). As a practical matter, most fields that

use statistical descriptions of their systems have

developed more-or-less distinct sub-disciplines that

study the two pictures, each with its own distinctive

tools and methods. In economics, for instance, the

Treasury and the Federal Reserve use

macroeconomic tools, theories and measures to

follow the economy as a whole, while investment

brokers use different tools to produce investment

strategies for individuals. The two pictures should be

exactly equivalent (and they are rigorously so for

systems like ideal gasses, if not necessarily so for

the economy) but nevertheless the two sub-

disciplines can often look very different.

In education too, different tools and methods

have traditionally been associated with individual

students than have been used with ensembles. In

particular, although tests can be (and sometimes

indeed are) used to guide individual students’

learning, most tests are mainly used to produce

grades (i.e. rankings). Concept Inventories on the

other hand are meant to map students’ prevalent

misconceptions in a field, and hence guide the

development of instructional materials and methods

that address these misconceptions explicitly. On the

student level, CIs can be used to assign supplemental

instructional materials that are specifically designed

to address that particular student’s misconceptions.

For example, during the development of the Biology

Concept Inventory (BCI), we discovered that an

entire class of difficulties that students encounter in

both genetics and molecular biology arise from

students’ misconceptions about random processes

(cf. Garvin-Doxas and Klymkowsky, 2008;

Klymkowsky and Garvin-Doxas, 2008). In short,

students do not understand that processes as diverse

as diffusion and evolution are underpinned by

random processes which are taking place all the time

(molecular collisions and mutations), but think

instead that they are driven processes that stop

taking place when the driver is removed (they

believe that there is no diffusion in the absence of

density gradients, and no evolution in the absence of

natural selection). This misconception can frustrate

learning unless it is directly addressed, and one can

envision instructional materials designed to address

it explicitly.

As a result of their main use as producers of

rankings, tests are therefore (in order of importance)

1) uni-dimensional 2) monotonic, and, as much as

possible, 3) linear. Of these properties, the one that

mostly defines the structure of a test is linearity.

2.1 Tests as Producers of Rankings

To ensure these properties, test developers look at

statistical measures like discrimination (ie. how

close can two scores be before we can no longer

assure that the higher score indeed represents higher

performance) and item difficulty.

Item difficulty is the fundamental weighting

factor on which most of the linearization schemes

rest. Perhaps the version of difficulty that is most

accessible intuitively is the percentage of students

that answered the question correctly; questions that

have been answered correctly by a large percentage

of students have lower difficulty. Item Response

Theory (IRT) for instance makes an explicit

assumption of true or near unidimensionality, and

posits that the probability, P, that a student of ability

 will correctly answer a question of difficulty b is

given by the logistic function

P = exp(

-b) / [1+exp(-b)]

(1)

Both student ability and item difficulty can then be

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

302

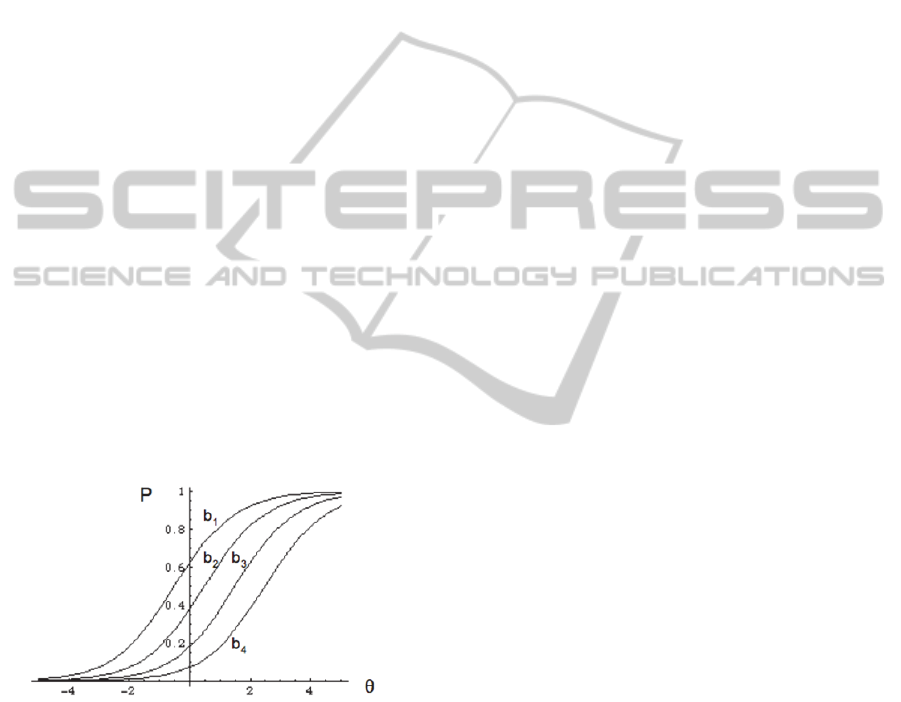
place on the same scale (as we see from the logistic

function, a student whose ability 

is equal to the

difficulty of some item b

will have a 50%

probability of answering that question correctly).

Difficulty is then used to linearize the response

of the test. The most intuitively accessible

linearization method, and the one most widely used,

consists of constructing the test with questions of

many different difficulty levels (b

-b

in Figure-1).

The higher the level of the student’s skill and

knowledge, the more questions s/he will answer

correctly. With a large bank of questions to choose

from, a test can be devised with questions that are

evenly spaced along the difficulty line, effectively

calibrating the instrument to insure a more-or-less

linear response: answering twice as many questions

(above some statistical floor) really means twice the

level of performance. We should note here that for

multiple choice tests the probability that a student of

very low ability answers correctly asymptotes to the

random floor (e.g. 25% for a four-option item), but

for concept inventories it usually asymptotes well

below the random floor, and often close to zero. This

is a consequence of having distracters that represent

common misconceptions; students who hold an

alternative model are lured to the answer that

corresponds to their model, and are therefore less

likely to pick the correct answer by chance.

Statistical treatments that take into account a

nonzero asymptote also exist.

Figure 1: Item Characteristic Curves (ICCs) for four items

of difficulty b

-b

. Evenly distributing test items along the

difficulty line produces a test with linear response.

Recently, more sophisticated linearization

techniques like Rasch analysis (Rasch, 1961) have

been used for instrument calibration, but all

calibration techniques aim for a linear instrument

response, and make explicit or implicit assumptions

about unidimensionality (or near-unidimensionality).

This is a direct and unavoidable consequence of

most tests’ main use, which is to produce rankings.

2.2 Concept Inventories and Rankings

Necessary as these statistical properties are for tests,

they are mostly irrelevant (and sometimes even

counterproductive) for Concept Inventories. CIs are

by nature multidimensional since what we really

want to know is each of the misconceptions that a

student holds, not some average over all

misconceptions. What we really want to know is

what specific instructional material to assign to a

student in order to address his/her misconceptions; a

measure of the student’s average performance level

is not at all informative on that task. Furthermore,

the percentage of students that answers a question

correctly is not an appropriate weighting factor for a

CI. The vast majority of the students can, and often

do, harbour the same misconception even after

repeated instruction; this is the very essence of

misconceptions. Leaving these questions out of the

instrument, or giving them minimal weight, because

they are at the tail of the difficulty distribution is not

a productive option.

Nevertheless, CIs have historically been used

essentially as tests, reporting a student’s

improvement in overall performance

(i.e. improvement in the total number of items

answered correctly) instead of reporting each

misconception a student is holding. This use of a CI

has proven to be useful in gaining the attention of

instructors (e.g. Hake, 1998), and should therefore

be considered during instrument constructions as a

possible (and even probable) use of the final

instrument. That said, results from CIs are inherently

much richer in the types of insights they can

provide. Given that the objective of a CI is to

provide detailed information that can be used to

explicitly address student misconceptions, it is

useful to have an analysis for each dimension

(concept) in the instrument, in addition to an average

over all dimensions. This can be done by performing

a statistical analysis not only for the correct answer

in each question, but also for the answers that

correspond to particular misconceptions. In the

context of IRT for instance, the Item Characteristic

Curve (ICC; Fig.-1) is no longer the probability that

the student will answer the question correctly, but

the probability that the student will pick the answer

that corresponds to a particular misconception, and 

is the student’s “ability” with respect to that

misconception, or in other words the degree to which

the student holds that misconception.

The requirement of performing an analysis for

each dimension of a CI revives “the curse of

dimensionality” (the requirement of analyzing a very

UsingTechnologytoAcceleratetheConstructionofConceptInventories-LatentSemanticAnalysisandtheBiology

ConceptInventory

303

large number of items) which is precisely the

problem that modern test theories aim to alleviate.

Nevertheless, the requirement is a direct

consequence of the function of CIs, which is to

produce multidimensional information on the

conceptual state of students.

2.3 Validity and Reliability

For an instrument to be useful, be it a test or a CI, it

must be valid and reliable. Validity means that the

instrument measures what we want it to measure,

and doesn’t measure things we don’t want it to

measure (a thermometer should measure only

temperature, not some combination of temperature

and weight). Reliability means that the instrument

gives the same value when measuring identical

things. It is obvious from the definitions that validity

and reliability are closely related; if an instrument

measures only one thing (eg. temperature) then

there’s only one value it can give (the temperature of

whatever we are studying, no matter what its other

properties are). It is therefore clear that validity

implies reliability. What is less appreciated however,

is that reliability does not imply validity. Reliability

means that we are consistently measuring the same

one thing; but what is that thing? The answer to that

question cannot possibly come from the statistics of

the instrument alone; an additional input is needed.

That additional input is always theory. The

statistics of a reliable thermometer are identical to

the statistics of a reliable voltmeter (in fact, most

modern thermometers are actually measuring a

voltage); the only difference is the theory used to

translate the output of the device into a measurement

of temperature. In CI construction that additional

input is provided by experts who can consistently

associate students’ verbal cues with persistent

mental constructs.

Validation is a labour intensive and time

consuming process, the cost of which we can reduce

significantly with the use of technology. During the

development of the BCI we created Ed’s Tools, an

online suite of tools that allows us to collect, code,

and aggregate large amounts of text data,

considerably improving the speed of data collection

and analysis. The validation procedure and

validation results for the BCI are described in detail

in Garvin-Doxas and Klymkowsky, 2008, and

Klymkowsky and Garvin-Doxas, 2008. The

development and usage of Ed’s Tools are described

in detail in Garvin-Doxas et. al., 2007. Here we give

a short description of the method for completeness,

while referring the reader to the previously

published work for a detailed exposition.

We start by asking students to provide essay

answers to open-ended questions, which we then

code using Ed’s Tools. The coding allows us to

aggregate the language that students use to describe

their thinking for each concept that we identify. We

then use that language to formulate both the

questions and the answers (both the correct answer

and the distracters) for the CI items. We then

conduct interviews and think-alouds with a large

number of students and use these to refine our

wording of the Inventory items, and repeat the cycle

until the results from the interviews and the

instrument converge.

In the following section we describe how we use

Latent Semantic Analysis (LSA) to improve the

logistics of determining the prevalence of each

preconception in the student population, and we

show some initial results.

2.4 Latent Semantic Analysis and CI

Construction

LSA has been used successfully to provide grading

of student essays that correlates well with grades

given by experts (Landauer and Dumais, 1997;

Landauer et a.l, 1998), and can also be used

effectively to provide feedback that helps students

(or teachers) identify the elements of the text that

they have missed (Kintsch et al., 2000).

In addition to these general language

applications, we have recently achieved comparable

results in science specific tasks. The results of this

work show that with only a small (of the order of

~100) set of human-rated documents to train on,

LSA can classify documents that it has not trained

on along predefined concept categories in a way that

correlates well with the human classification. So far

we have analyzed student answers to three questions

in Physics, two in Astronomy, and six in Biology.

The Physics results shown in Figure-2 were

obtained with data collected with Ed’s Tools from

three different classes at the University of Northern

Colorado (UNC): an introductory calculus-based

course for scientists and engineers, and two physics

courses for pre-service teachers (an introductory

physics course, and a capstone physics course that is

required of all graduating pre-service teachers). The

essay was assigned during regular class time, and

students in all three classes were given 20 min to

complete it. The essay was given early in the

semester so that the students in the calculus based

class and the introductory pre-service class had not

covered the material in college.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

304

A typical Physics question was:

In 60 words or more, describe what happens

when a light car and a heavy truck, which travel

with the same speed but in opposite directions,

collide head-on?

As a rule of thumb sixty-word answers are the

shortest documents on which LSA can be effective,

but with this question we wanted to test LSA’s

performance for the shortest answers on which the

method can be expected to give reasonable results.

We collected 65 responses from a class for majors,

and a total of 160 responses from two classes for

pre-service teachers. Although the overall number of

essays we collected was 225, nearly half of them had

no physics content (most of the invalid responses

concerned seat belt use, insurance rates, and the

safety disadvantages of fuel efficient small cars) so

the number of relevant essays on which LSA trained

was closer to 120. Two expert graders used

approximately half of the responses to train on, and

scored the remaining half independently. Four rubric

components were identified, along which each of the

answers was scored on a scale of 0-3. An answer

was given a 0 along a component if it did not contain

any treatment of the subject, and a 3 if it contained a

well articulated treatment (for a misconception, that

treatment is physically incorrect, but as long as the

concept is clearly present in the text the score for

that component is 3). The four components and

examples of answers are given in the Appendix. The

essays were analyzed using two spaces, TASA, and

a physics space constructed for the project. TASA

contains 1.2 million words in 37,000 documents and

750,000 sentences and has been selected to be

representative of the amount and type of material a

college student would have read in their lifetime.

The physics space was constructed using

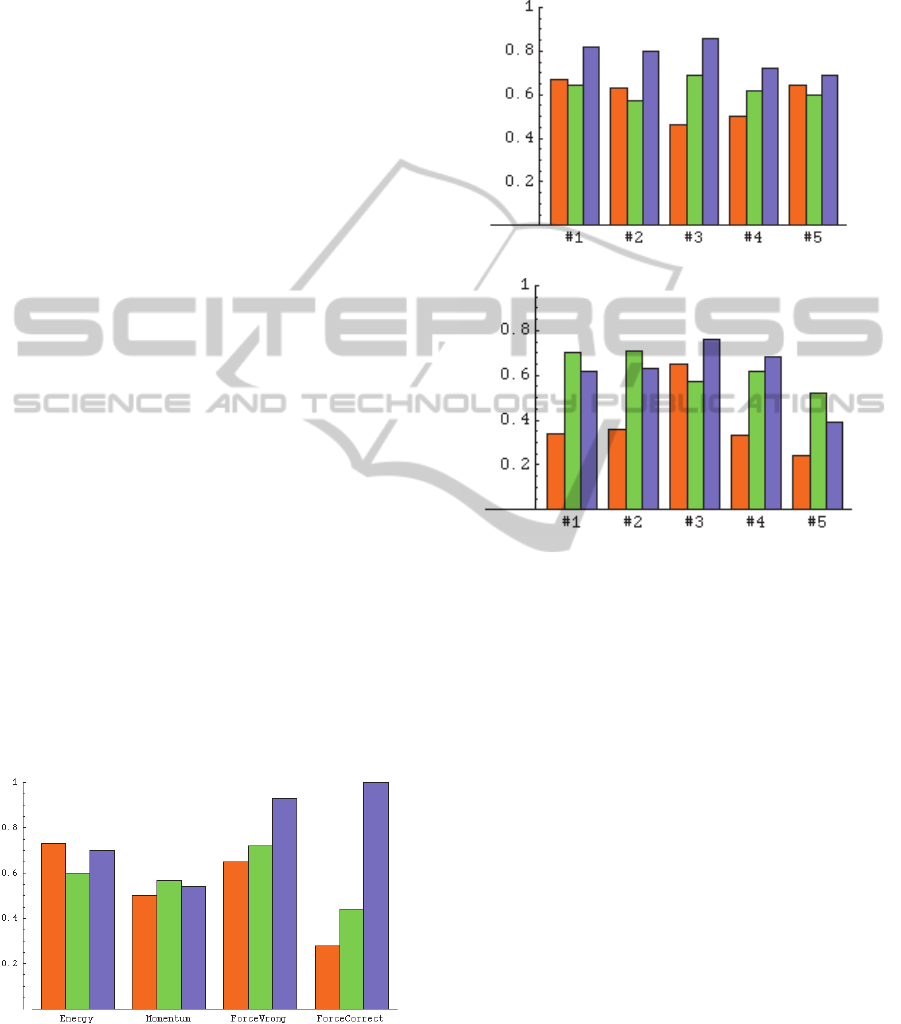
Figure 2: The correlation between the LSA score

assignment and the experts’ score assignment for each

rubric component. The bars represent the TASA-Expert,

(TASA+Physics)-Expert, and Expert-Expert correlations

respectively for the orange, green, and blue bar.

introductory physics texts available under the Open

Content license (http://opencontent.org/opl.shtml)

and contains 1465 documents.

Astronomy

Biology

Figure 3: Top frame: The correlation function between the

two experts (blue) and between the experts and the LSA

system using the TASA general English space (orange)

and TASA augmented with the physics space (green). The

rubric components are as follows:

#1: The Cosmological Constant (CC) provides a repulsive

force that counteracts gravity

#2: The CC is the same as Dark Energy

#3: Study of distant supernovae shows that the expansion

of the universe is accelerating

#4: Fluctuations in the microwave background radiation

show that the CC exists

#5: Dark Energy is a force that counteracts gravity

Bottom frame: The correlation function between the two

experts (blue) and between the experts and the LSA

system using the TASA general English space (orange)

and TASA augmented with the biology space (green). The

rubric components are as follows:

#1: Alternative forms of a gene are known as alleles

#2: Alleles can be dominant or recessive to one another

#3: For most genes, you carry two alleles, one from your

mother and the other from your father

#4: A recessive phenotype is visible if both alleles are

recessive; if one is dominant, the recessive phenotype will

not be visible, but the allele remains and can be passed to

offspring

#5: Phenotype refers to the visible traits displayed by an

organism.

UsingTechnologytoAcceleratetheConstructionofConceptInventories-LatentSemanticAnalysisandtheBiology

ConceptInventory

305

Figure-1 shows the correlation of the LSA

assigned scores (using the two spaces) to the score

assigned by expert-1 for each of the components,

and the correlation between the two experts.

Dimension-3 is the well-known dominant

misconception in the domain (that the heavy truck

will exert a greater force on the small car than the

other way around). We see that LSA is comparable

to the experts for component-1 (correct energy

formulation) and component-2 (correct momentum

formulation), although it performs lower than the

experts in component-3 (the dominant

misconception on the subject). Component-4 is the

correct force formulation of the problem.

It is important to note that TASA alone, which is

general space, produces results that are overall

comparable to the results produced with the addition

of a target-specific physics space. This plot shows

that by using human raters to rate a relatively small

number of documents, LSA can generally classify

documents on which it was not trained, with a

correlation which can be comparable to that of

different human experts. The exception in this case

seems to be the correct force formulation (which

states that the forces exerted by the car and truck on

each other are equal). It is not clear why this rubric

component faired so much worse than the rest. It is

worth noting that the experts were in perfect

agreement on this component (the correlation is one,

over all relevant answers).

Figure-3 shows results from two additional

questions, one in Astronomy, analyzed with TASA

and the same Physics test used in the Physics

questions, and one in Biology, analysed with TASA

and an open source Biology text. We see that in both

cases the system is consistently comparable to the

experts, especially when the general English space is

augmented with subject-specific texts.

3 CONCLUSIONS AND FUTURE

WORK

Although this is an ongoing project, the results so far

show that student essays, even of lengths that are

generally on the borderline of being too short for

treatment by LSA, can indeed give results that are

comparable to expert raters’, although some

challenges still remain. One of the questions that

will be important to the method, is the extend to

which the nature of the space in which the texts are

projected (eg. a general space like TASA versus a

discipline-specific space like the one we developed

from the textbooks) affects performance, and we

plan to conduct additional studies with a variety of

discipline-specific texts to address this question.

Perhaps the greatest limitation of the method is the

fact that, at this stage, the dominant misconceptions

are still being discovered “by hand” as it were, with

experts combing through large amounts of textual

data. Tools like Ed’s Tools can improve the logistics

of that search, and tools like LSA can improve the

logistics of identifying these misconceptions in very

large populations, but the discovery phase still

depends exclusively on experts. We plan to address

this limitation in future work, by using LSA to point

out possible new misconceptions that can then be

rated by content experts.

REFERENCES

Bloom, B. S., The 2 Sigma Problem: the Search for

Methods of Group Instruction as Effective as One-on-

One Tutoring, Educ. Res. 13, 4 (1984).

Garvin-Doxas, K. and M. W. Klymkowsky.

Understanding Randomness and its impact on Student

Learning: Lessons from the Biology Concept

Inventory (BCI). CBE Life Sci Educ 7: 227-233

(2008).

Garvin-Doxas, K., I. Doxas, and M.W. Klymkowsky. Ed's

Tools: A web-based software toolset for accelerated

concept inventory construction. Proceedings of the

National STEM Assessment Conference 2006. D.

Deeds & B. Callen, eds. Pp. 130-139 (2007).

Hake, R., Interactive engagement versus traditional

methods: A six-thousand-student survey of mechanics

test data for introductory physics courses, American

Journal of Physics, 66, pp. 64 (1998).

Kalas P, O'Neill A, Pollock C, Birol G., Development of a

meiosis concept inventory, CBE Life Sci Educ.

12(4):655-64. doi: 10.1187/cbe.12-10-0174 (2013).

Kintsch, E., D. Steinhart, G. Stahl, Developing

summarization skills through the use of LSA-based

feedback, Interactive Learning Environments, 8

(2000).

Klymkowsky, M.W. and K. Garvin-Doxas. Recognizing

Student Misconceptions through Ed's Tool and the

Biology Concept Inventory. PLoS Biology, 6(1): e3.

doi:10.1371/journal.pbio.0060003, (2008).

Landauer, T. K., P. Foltz, and D. Laham, An introduction

to Latent Semantic Analysis. Discourse Processes, 25,

259-284 (1998).

Landauer, T. K. and Dumais, S. T., A solution to Plato's

problem: the Latent Semantic Analysis theory of

acquisition, induction and representation of

knowledge. Psychological Review, 104(2), 211-240

(1997).

Libarkin, J., and S. Anderson, Development of the

Geoscience Concept Inventory, Proceedings of the

National STEM Assessment Conference, Washington

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

306

DC, p. 148-158, (2006).

McDermott, L.C., P.S. Schaffer, and the Physics

Education Group at the University of Washington,

Tutorial in Introductory Physics, Prentice Hall, New

York (1998).

Midkiff, K. C., T. A. Litzinger, D. L. Evans, Development

of Engineering Thermodynamics Concept Inventory

Instrument, 31st ASEE/IEEE Frontiers in Education

Conference, Reno, NV (2001).

Rasch, G. On General Laws and the Meaning of

Measurement in Psychology. Proceedings of the

Fourth Berkeley Symposium on Mathematical

Statistics and Probability, Volume 4: Contributions to

Biology and Problems of Medicine, 321--333,

University of California Press, Berkeley, Calif.,

(1961).

Smith, M. K., W. B. Wood, and J. K. Knight, The

Genetics Concept Assessment: A New Concept

Inventory for Gauging Student Understanding of

Genetics, CBE Life Sci Educ 7, 422, (2008).

Zeilik, Michael, C. Schau, N. Mattern, S. Hall, K. W.

Teague, and W. Bisard, Conceptual astronomy: A

novel approach for teaching postsecondary science

courses. American Journal of Physics 65:10, 987-996,

(1997).

APPENDIX

The rubric components for the Physics example:

Component-1: Energy Conservation

Answers that received a non-zero grade along this

component had a correct discussion of energy

conservation for the problem. Students usually

talked about kinetic energy being converted to other

forms of energy during the collision (eg. heat or

sound) and correctly stated that the total kinetic

energy after the collision is lower than before. Some

students even identified and explained elastic and

inelastic collisions. The more complete the answer,

the higher the score that was assigned to it in this

component. For example:

When the light car and heavy truck collide. Each

will apply a force to the other. The force from the

heavy truck will be greater than the force the car

applies to the truck. After the inelastic collision the

car will "bounce" off the truck and travel

backwards. The truck will slow considerably but

should continue forwards. In this collision

momentum of the car and truck system will be

conserved because momentum is always conserved.

Kinetic energy however will be lost because the

collision is inelastic. Energy will be lost in the form

of heat and sound.

This answer was scored as a 3 in the first

component (incidentally, it also scored a 3 in

component-3, the dominant misconception in the

domain).

Component-2: Momentum Conservation

Answers that received a non-zero score along this

component had a correct discussion of momentum

considerations for the problem. Students usually

talked about the truck having a greater momentum

because of its greater mass. They correctly stated

that the truck will continue to move in its original

direction, while the car will reverse directions, that

the combined mass of the car+truck will move at a

lower speed than either did before, and many

students even stated explicitly that momentum is

conserved in the collision. The more complete the

answer, the higher the score that was assigned to it

along this component. For example:

What happens when the light car and heavy truck

collide with each other is that they will have a non-

elastic collision. When they crash they will

somewhat stick together and continue to move in the

same direction as the heavy truck was moving before

the collision. The kinetic energy of the light car and

heavy truck will not be the same as the kinetic

energy of the total mass of the truck and car,

because the vehicles are not on a frictionless surface

and energy is lost in heat.

This answer scored a 3 in this component

(although it is missing an explicit statement for

conservation of momentum). It also scored a 3 in

component-1 (correct energy treatment) despite the

fact that it is ambiguous about the reason for energy

non-conservation. Very few answers were better

than this.

Component-3: The Force Exerted by the Truck is

Bigger

This is the best known misconception treated in the

literature. Answers that received a non-zero grade

along this component stated that the truck will exert

a bigger force on the car than the other way around.

For example:

Primarily, when a collision occurs between any

object, energy will always be conserved. What will

happen in a case where a light car and a heavy

truck, traveling at the same speed in opposite

directions, collide is each will have a certain

magnitude in force and after the collision the

vehicles will travel some distance. We know that the

heavier truck will have more force because it is

more massive. The light car will have less force

because it is less massive. The direction in which the

vehicles travel post impact depends on the net force

resulting between the two vehicles.

This answer scored a 3 in this component. It

clearly states the dominant misconception twice,

UsingTechnologytoAcceleratetheConstructionofConceptInventories-LatentSemanticAnalysisandtheBiology

ConceptInventory

307

both for the truck and for the car.

Component-4: Force Equal

This is the correct force formulation for the problem.

According to Newton’s laws, the force exerted by

the car on the truck is equal to the force exerted by

the truck on the car. For example:

When a light car and heavy truck collide head on

traveling at the same speed the light car will have

the most damage. This is not because the force was

greater on the car, both are hit with the same

amount of force, it is simply because the car is not

built as sturdy as the heavy truck.

This answer received a 3 on this component.

Some students not only stated this explicitly, but

they also quoted Newton’s law by name.

CSEDU2014-6thInternationalConferenceonComputerSupportedEducation

308