
Optimal Feedback Control for a Perimeter Traffic Flow at an Urban
Region
Jack Haddad and Ilya Ioslovich
Technion Sustainable Mobility and Robust Transportation (T-SMART) Laboratory,
Faculty of Civil and Environmental Engineering, Technion–Israel Institute of Technology, Haifa, Israel
Keywords:
Perimeter Traffic Control, Macroscopic Fundamental Diagram, Optimal Control.
Abstract:
Traffic flow control has motivated many researchers since early decades of the 19th century. Recently, the
concept of a perimeter traffic control for an urban region has been strengthened by a series of works, which
have shown that a perimeter controller, located at a region border, can manipulate the transfer flows across
the border to maximize the total outflow of the region. The macroscopic fundamental diagram (MFD), that
relates average flow with accumulation, is used to model the traffic flow dynamics in the region. Assuming
that the control inputs of the cross-border flows are coupled, i.e. the border is always utilized over time for
transferring flows by one of the two directions (from and towards the region), and that the urban region has
two traffic flow demands generated inside the region with internal and external destinations, and a generated
traffic flow outside the region with a destination to the region, the explicit formulation of the optimal feedback
control policy and a proof of optimality are provided. The proof is based on the modified Krotov-Bellman
sufficient conditions of optimality, where the upper and lower bounds of state variables are calculated.
1 INTRODUCTION
In the last decade, network traffic flow modeling with
the Macroscopic Fundamental Diagram (MFD) repre-
sentation has intensively attracted the traffic flow and
control researchers. The MFD simplifies the mod-
elling task of the traffic flow dynamics for large-scale
urban networks, as it provides aggregate relationships
between traffic variables at an urban region.
The MFD provides a unimodal, low-scatter rela-
tionship between network vehicle density (veh/km)
or accumulation (veh) and network space-mean flow
(outflow) (veh/hr) for different network regions, if
congestion is roughly homogeneous in the region.
The physical model of the MFD was initially pro-
posed by (Godfrey, 1969), but the theoretical ele-
ments for the existence of the MFD were provided
later by (Daganzo, 2007). The MFD was first ob-
served with dynamic features in congested urban net-
work in Yokohama by (Geroliminis and Daganzo,
2008), and investigated using empirical or simulated
data by (Buisson and Ladier,2009; Ji et al., 2010; Ma-
zloumian et al., 2010; Daganzo et al., 2011; Gayah
and Daganzo, 2011; Zhang et al., 2013; Mahmassani
et al., 1987; Olszewski et al., 1995) and others.
Homogeneous networks with small variance of
link densities have a well-defined MFD (as illustrated
in Fig. 1(a)), i.e. low scatter of flows for the same
densities (or accumulations), (Geroliminis and Sun,
2011b; Mazloumian et al., 2010; Daganzo et al.,
2011; Knoop et al., 2013; Mahmassani et al., 2013).
Note that heterogeneous networks might not have
well-defined MFDs, mainly in the decreasing part of
the MFD, as the scatter becomes higher as accumu-
lation increases and hysteresis phenomena has been
found to exist (Daganzo et al., 2011; Buisson and
Ladier, 2009; Saberi and Mahmassani, 2012; Geroli-
minis and Sun, 2011a). As a solution, these networks
might be partitioned into more homogeneous regions
with small variances of link densities, (Ji and Geroli-
minis, 2012). Note that the network topology, the sig-
nal timing plans of the signalized intersections inside
the region, and the infrastructure characteristics af-
fect the shape of the MFD, see e.g. (Geroliminis and
Boyacı, 2012).
The MFD concept has been utilized to introduce
control policies that aim at improving mobility and
decreasing delays in large urban networks, (Daganzo,
2007; Haddad and Geroliminis, 2012; Geroliminis
et al., 2013; Hajiahmadi et al., 2013; Haddad et al.,
2013; Aboudolas and Geroliminis, 2013; Keyvan-
Ekbatani et al., 2012; Knoop et al., 2012; Zhang et al.,
14
Haddad J. and Ioslovich I..
Optimal Feedback Control for a Perimeter Traffic Flow at an Urban Region.
DOI: 10.5220/0005009800140020
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 14-20
ISBN: 978-989-758-039-0
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

2013). E.g. perimeter control strategies, i.e. ma-
nipulating the transfer flows at the perimeter border
of the urban region, have been introduced for single-
region cities in (Daganzo, 2007; Keyvan-Ekbatani
et al., 2012; Shraiber and Haddad, 2014), and for
multi-region cities in (Geroliminis et al., 2013; Had-
dad et al., 2013; Hajiahmadi et al., 2013; Aboudolas
and Geroliminis, 2013). In this paper, we deal with
perimeter control for a single urban region modelled
by an MFD.
Different control approaches have been proposed
to solve perimeter control problems for single-region
cities. (Daganzo, 2007) has presented a bang-bang
control as an optimal control policy for an urban re-
gion. A Proportional-Integrator (PI) perimeter con-
troller has been designed for an urban region in
(Keyvan-Ekbatani et al., 2012). The formulated non-
linear system is linearized around a priori known set-
point chosen carefully within a value range in the un-
congested regime of the MFD having positive slope
and close to the critical state (total time spent) of the
MFD function. The work in (Keyvan-Ekbatani et al.,
2012) aims at regulating the dynamic system around
the desired chosen set-point, at which the system’s to-
tal time spent is minimized, in other words, the state
reference is the same as the set-point. Moreover, the
work in (Keyvan-Ekbatani et al., 2012) do not allow
direct consideration of the control constraints, but im-
pose them after the design process, e.g. adjusting or
fine-tuning the controller gains.
In (Shraiber and Haddad, 2014), a robust perime-
ter controller has been designed for an urban region
with the MFD representation. The designed controller
is a fixed PI-controller with proportional K
P
and inte-
grator K
I
gains, which stabilizes the linearized system
against MFD and parameter uncertainties. The ro-
bust controller is also designed to handle control con-
straints within the design level in a systematic way.
The results showed that the controller has performed
well for the whole state set, and not necessary for a
value range nearby a set-point.
In this paper, the optimal feedback control for a
perimeter traffic flow at an urban region is derived,
and a proof of optimality is provided with the help
of the modified Krotov-Bellman sufficient conditions
of optimality. The region is assumed to be a ho-
mogeneous region having a well-defined MFD with
two traffic flow demands generated inside the region
with internal and external destinations, and a gener-
ated traffic flow outside the region with a destination
to the region.
2 OPTIMAL PERIMETER
CONTROL: PROBLEM
DEFINITION
This paper deals with a perimeter control problem for
a homogeneous urban region having a well-defined
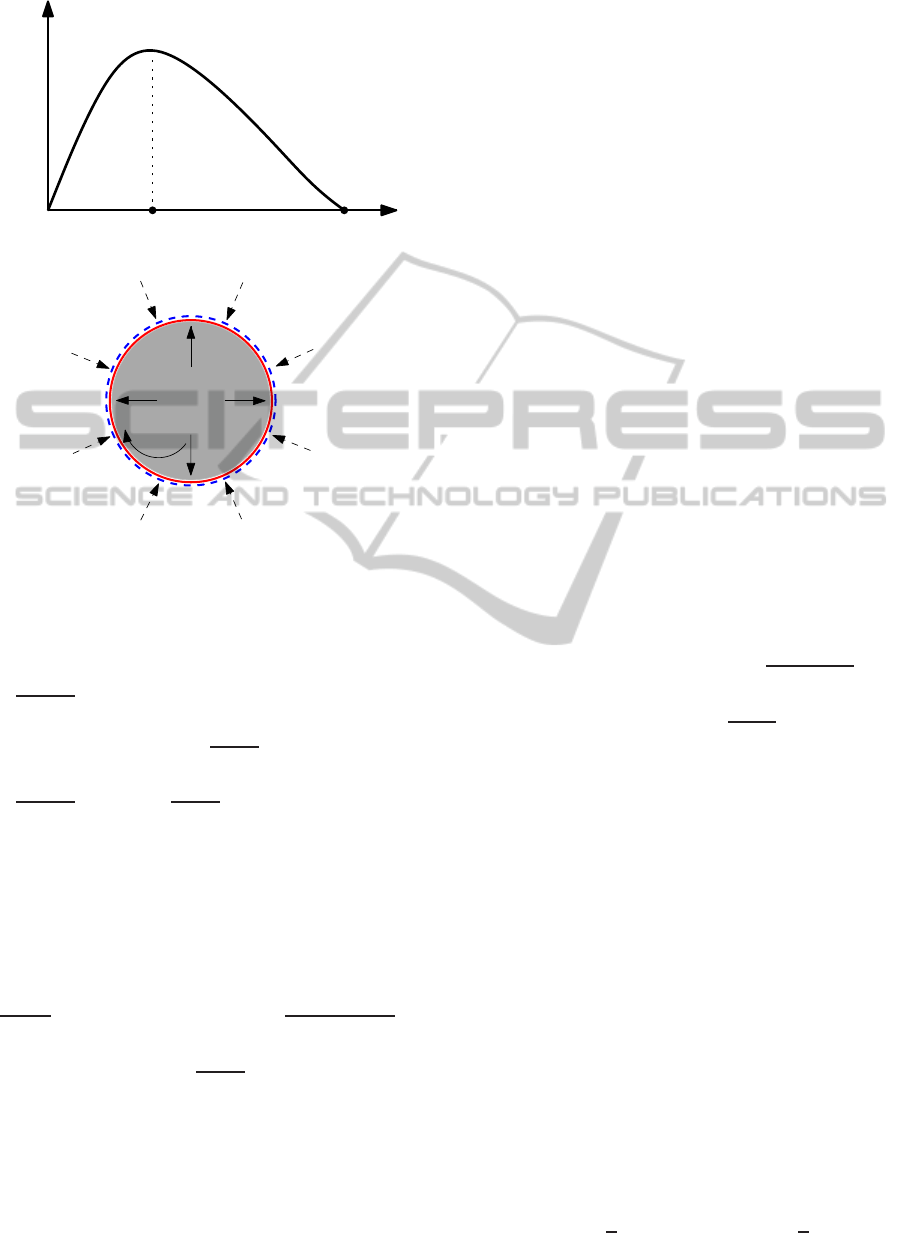
MFD, schematically shown in Fig. 1. The flow dy-
namic equations for a homogeneous urban region
have been already formulated in (Shraiber and Had-
dad, 2014), and they are briefly presented as follows.
There are two state variables denoted by n
11
(t) and
n
12
(t) (veh), which respectively represent the num-
ber of vehicles traveling in the region with destina-
tion inside and outside the region at time t. The to-
tal accumulated number of the vehicles in the region
is n
1
(t) = n
11
(t) + n
12
(t). The MFD links the accu-
mulation, n
1
(t), and trip completion flow, defined as
the output flow of the region. The MFD provides a
low-scatter relationship, if congestion is roughly ho-
mogeneous in the region. The MFD is denoted by
G
1
n
1
(t)
(veh/s), and it is assumed to be Lipschitz,
continuous, non-negative, and unimodal. This as-
sumption is based on many simulation and empiri-
cal results, e.g. in (Geroliminis and Daganzo, 2008).
The MFD is defined as the trip completion flow for
the region at n
1
(t): (i) the sum of a transfer flow,
i.e. trips from the region with external destination
(outside the region), plus (ii) an internal flow, i.e.
trips from the region with internal destination (in-
side the region). The transfer flow is calculated cor-
responding to the ratio between accumulations, i.e.
n
12
(t)/n
1
(t)·G
1
n
1
(t)
, while the internal flow is cal-
culated by n
11
(t)/n
1
(t) · G
1
n
1
(t)
.
The traffic flow demands generated in the region
with internal and external destinations are respec-
tively denoted by q
11
(t) and q
12
(t) (veh/s), while
q
21
(t) (veh/s) denotes a generated traffic flow outside
the region with destination to the region, as schemat-
ically shown in Fig. 1(b). Following (Shraiber and
Haddad, 2014), a perimeter control is introduced on
the border of the urban region, where its inputs are
coupled u(t) (− ) and 1 − u(t) and control the ratios
of flows, 0 ≤ u(t) ≤ 1, that cross the border from in-
side to outside and from outside to inside the region at
time t, respectively, see Fig. 1(b). It is also assumed
that the perimeter control will not change the shape of
the MFDs. Note also that the internal flow cannot be
controlled or restricted.
The vehicle-conservation equations in the urban
regions are given as follows (same equations (1) and
(2) in (Shraiber and Haddad, 2014)):
OptimalFeedbackControlforaPerimeterTrafficFlowatanUrbanRegion
15
G
1
(n
1
(t)) (veh/s)
Trip completion flow
n
1,max
n
∗
1
Accumulation, n
1
(t) (veh)
(a)
1 − u(t)
q
21
(t)
q
11
(t)
q
12
(t)
u(t)
12
(b)
Figure 1: (a) A schematic MFD which is Lipschitz, con-
tinuous, non-negative, and unimodal function, (b) An urban
region with three traffic demand q
11
(t), q
12
(t), q
21
(t), and
a perimeter controller with inputs u(t) and 1− u(t).
dn
11
(t)
dt
= q
11
(t) + (1− u(t)) · q
21
(t)
−
n
11
(t)
n
1
(t)
· G
1
n
1
(t)
,
(1)
dn
12
(t)
dt
= q
12
(t) −
n
12
(t)
n
1
(t)
· G
1
n
1
(t)
· u(t). (2)
Let us now rewrite (1) to have a state equation cor-
responding to variable n
1
(t) instead of n
11
(t). The
reason for that is only technical as this simplifies the
mathematical proofs given later in Section 3. By sum-
ming (1) and (2) and substituting n
11
(t) = n
1
(t) −
n
12
(t), one gets
dn
1
(t)
dt
= q
11
(t) + q
12
(t) + q
21
(t) −
n
1
(t) − n
12
(t)
n
1
(t)
· G
1
n
1
(t)
−
q
21
(t) +
n
12
(t)
n
1
(t)
· G
1
n
1
(t)
· u(t).
(3)
The optimal control problem aims at manipulating the
control input u(t) to optimize an objective J, subject
to (2) and (3). There are a variety of criteria that can
be chosen, e.g. the throughput of the transportation
network and the total network delay. In this paper,
the throughput of the transportation network in the re-
gion is chosen, which is defined as the total number
of vehicles that complete their trips and reach their
destination during the time interval [t
0
,t
f
], i.e.
J
1
=
Z
t
f
t
0
G
1
n
1
(t)
dt, (4)
where t
0
and t
f
(s) are the starting and final times of
the control process. Note that the defined problem
here is an optimal control problem, while in (Shraiber
and Haddad, 2014) the problem is defined as a regu-
lator control problem.
3 OPTIMAL CONTROL DESIGN
The MFD function G
1
n
1
(t)
is assumed to be uni-
modal with a single maximum value at n
∗
1
(veh), see
also Fig. 1(a), i.e.
n
∗
1
= argmax
n
1
(t)
G
1
n
1
(t)
. (5)
Let us denote u
ss
(t) (−) as the steady-state control
input, which corresponds to a steady-state condition
dn
1
/dt = 0, at n
1
(t) = n
∗
1
, i.e. the steady state control
input u
ss
(t) is calculated from (3) with dn
1
/dt = 0 and
n
1
(t) = n
∗
1
, as follows:
u
ss
(t) =
q
11
(t) + q
12
(t) + q
21
(t) −
n
∗
1
− n
12
(t)
n
∗
1
· G
1
(n
∗
1
)
/
q
21
(t) +
n
12
(t)
n
∗
1
· G
1
(n
∗
1
)
.
(6)
Note that u
ss
(t) is a time dependent corresponding to
the traffic demands q
11
(t), q
12
(t), and q
21
(t).
Theorem 3.1. The optimal feedback control u
∗
(n
1
)
for the problem P1: max
u(t)
J
1
subject to (2) and (3)
is as follows:
If n
1
(t) 6= n
∗
1
, then
u
∗
(n
1
) =
(
0 ∀n
1
(t) < n
∗
1
,
1 ∀n
1
(t) > n
∗
1
,
(7)
otherwise (n
1
(t) = n
∗
1
),
u
∗
(n
∗
1
) =
u
ss
(t) 0 ≤ u
ss
(t) ≤ 1,
0 u
ss
(t) < 0,
1 u
ss
(t) > 1.
(8)
Proof. The proof is based on the unimodality assump-
tion of the function G
1
(n
1
(t)). The unimodal func-
tion G
1
(n
1
(t)) has the point-wise maximum for each
point t at n
1
(t) =
n
1
(t) if n
1
(t) ≤ n
∗
1
and n
1
(t) is an
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
16

upper bound of n
1
(t). Similarly, G
1
(n
1
(t)) has the
point-wise minimum for each point t at n
1
(t) = n
1
(t)
if n
1
(t) ≥ n
∗
1
and n
1
(t) is a lower bound of n
1
(t). The
upper bound
n
1
(t) and the lower bound n
1
(t) have to
be found with respect to the dynamical state equa-
tions (2) and (3) with initial conditions n
1
(t
0
) = n
1,0
,
n
12
(t
0
) = n
12,0
(see Lemmas 3.3 and 3.4). To com-
plete the proof we shall use the sufficient global op-
timality conditions in the form of modified Krotov-
Bellman conditions (see sections 3.1 and 3.2) and
prove Lemmas 3.2, 3.3, and 3.4 in Section 3.3.
According to (8), the optimal feedback control for
n
1
(t) = n
∗
1
is u
∗
(n
∗
1
) = u
ss
(t), where u
ss
(t) has to sat-
isfy the control constraint 0 ≤ u
ss
(t) ≤ 1. However,
if u
ss
(t) < 0 or u
ss
(t) > 1, then the optimal feedback
control is respectively u
∗
(n
∗
1
) = 0 or u
∗
(n
∗
1
) = 1. Note
that in the latter two cases the state cannot be kept
at n
∗
1
, since if u
ss
(t) < 0 the variable n
1
(t) will de-
crease from n
1
(t) = n
∗
1
even with all feasible u(t), but
the minimum decrease is achieved by u(t) = 0, and if
u
ss
(t) > 1 then n
1
(t) will increase for all feasible u(t),
but the minimum increase is achieved by u(t) = 1.
This is explained as follows. Let us first respectively
denote a(t) and b(t) as follows:
a(t) = q
11
(t) + q
12
(t) + q
21
(t) −
n
∗
1
− n
12
(t)
n
∗
1
· G
1
(n
∗
1
),
(9)
b(t) = q
21
(t) +
n
12
(t)
n
∗
1
· G
1
(n
∗
1
), (10)
then, (3) is rewritten as
dn
1
(t)
dt
= a(t) − b(t) · u(t) (11)
where b(t) ≥ 0, and a(t)−b(t)· u
ss
(t) = 0. Therefore,
if u
ss
(t) < 0 ≤ u(t) then dn
1
/dt = a(t) − b(t) · u(t) <
a(t) − b(t) · u
ss
(t) = 0, and if u
ss
(t) > 1 ≥ u(t) then
dn
1
/dt = a(t) − b(t) · u(t) > a(t) − b(t) · u
ss
(t) = 0.
3.1 Modified Krotov-Bellman Sufficient
Conditions of Optimality
The Krotov-Bellman sufficient conditions of optimal-
ity are summarized as follows. The reader can refer
to (Krotov, 1996) for further information. Given a dy-
namic system
dx
dt
= f(t, x,u), (12)
with state variables x(t), control inputs u(t), initial
conditions x(t
0
) = x
0
, and the following objective
function
minJ =
Z
t
f
t
0
f
0
(t,x,u)dt, (13)
one can construct a function R(t, x,u) as follows
R(t, x,u) =
∂V
∂x
f(t, x,u) − f
0
(t,x,u) +
∂V
∂t
, (14)
where V(t,x) is assumed to be a continuous and dif-
ferentiable function. Taking into account that the full
time derivative of V(t,x) with respect to (12) is
dV
dt
=
∂V
∂x
f(t, x,u) +
∂V
∂t
, (15)
and substituting (15) and (14) in (13), one gets
J = V(t
f
,x(t
f
)) −V(t
0
,x
0
) −
Z
t
f
t
0
R(t, x,u)dt. (16)
The sufficient Krotov-Bellman conditions of optimal-
ity are as follows: if there exists a pair (x
∗
,u
∗
) such
that x
∗
is the solution of the dynamic system
dx
∗
dt
= f(t, x
∗
,u
∗
) (17)
over the time interval [t
0
,t
f
], and the following prop-
erties
u
∗
= argsup
u
R(t, x,u),
R(t, x,u
∗
) = µ(t), (18)
Θ = V(t
f
,x(t
f
)) = Constant,
hold, then this pair (x
∗
,u
∗
) is a global optimum solu-
tion. Note that µ(t) is any measurable bounded func-
tion of t. According to these sufficient conditions of
optimality, the problem is reduced to a solution of
the nonlinear Krotov-Bellman PDE for the function
V(t,x).
In this paper, the modified Krotov-Bellman con-
ditions are proposed, where the maximization of
R(t, x,u) over u in (18) is replaced by the maximiza-
tion of R(t, x,u) over x, as follows:
x
∗
= argsup
x
R(t, x,u),
R(t, x
∗
,u) = µ(t) , (19)
Θ = V(t
f
,x(t
f
)) = Constant.
Note that in both variants (18) and (19), the resulting
function R(t,x,u) after maximization, i.e. R(t, x,u
∗
)
and R(t,x
∗
,u), respectively, will be a function of time
t only.
3.2 Application to the Maximum
throughput Objective
Applying the modified Krotov-Bellman conditions to
the problem (2)–(4), one gets
OptimalFeedbackControlforaPerimeterTrafficFlowatanUrbanRegion
17

sup
n
1
(t),n
12
(t)
∂V
∂n
1
q
11
(t) + q
12
(t) + q
21
(t)
−
n
1
(t) − n
12
(t)
n
1
(t)
G
1
(n
1
(t)) −
q
21
(t) +
n
12
(t)
n
1
(t)
· G
1
(n
1
(t))
· u(t)
+
∂V
∂n
12
(t)
q
12
(t) −
n
12
(t)
n
1
(t)
· G
1
(n
1
(t)) · u(t)
+ G
1
(n
1
(t)) +
∂V
∂t
= µ(t) ,
(20)
Θ = V(t
f
,n
1
(t
f
),n
12
(t
f
)) = Constant. (21)
Note that (20) and (21) are without taking into ac-
count the upper and lower bound constraints on state
variable n
1
(t), i.e.
g
1
(t) = n
1
(t) − n
1
(t) ≤ 0, (22)
g
1
(t) = n
1
(t) − n
1
(t) ≤ 0. (23)
Let
λ
1
and λ
1
be the Lagrange multipliers for
(22) and (23), respectively. Now, let us choose
V(t,n
1
(t),n
12
(t)) = C, where C is a constant. Then,
imposing state constraints (22) and (23) on (20) and
(21) with V(t, n
1
(t),n
12
(t)) = C, one gets
sup
n
1
(t)
[G
1
(n
1
(t)) −
λ
1
· g
1
(t) − λ
1
· g
1
(t)] = µ(t),
(24)
Θ = C. (25)
Note that Lagrange multipliers are taken with sign
minus because of maximization of J
1
. According to
Karush-Kuhn-Tucker (KKT) conditions all Lagrange
multipliers are non-negative and may have positive
values only when the corresponding constraint is
binding, i.e. non-redundant. From maximization of
(24), one gets
∂G
1
∂n
1
−
λ
1
+ λ
1
= 0. (26)
This implies that n
1
(t) =
n
1
(t) when
∂G
1
∂n
1
> 0, i.e.
when n
1
(t) < n
∗
1
(because G
1
n
1
(t)
is assumed to
be unimodal with a single maximum value at n
∗
1
), and
n
1
(t) = n
1
(t) when
∂G
1
∂n
1
< 0, i.e. when n
1
(t) > n
∗
1
.
Note that Lagrange multipliers for upper and lower
constraints cannot be non-zero simultaneously, and
because of unimodality the only point when
∂G
1
∂n
1
= 0
is the point n
1
(t) = n
∗
1
.
3.3 Upper and Lower Bounds of State
Variable n
1
(t)
Recall that to complete the proof of Theorem 3.1, the
upper bound n
1
(t) and the lower bound n
1
(t) have to
be found with respect to the dynamical state equa-
tions (2) and (3) with initial conditions n
1
(t
0
) = n
1,0
,
n
12
(t
0
) = n
12,0
. In this section, it is explained how to
achieve the upper bound
n
1
(t) and the lower bound
n
1
(t), according to Lemmas 3.3 and 3.4, respectively.
But first Lemma 3.2 is presented, which is taken from
(Krotov et al., 1971) and utilized to prove Lemmas 3.3
and 3.4.
Lemma 3.2. Consider an ODE system dx/dt =
f(x,u,t), where f(x,u,t) is Lipschitz and continuous
vector-function, x(t) = [x
1
(t),x
2
(t),.. . ,x
n
(t)]
T
are
the state variables, and u(t) are measurable bounded
control inputs. The upper bound of the solution x(t)
with initial conditions x(t
0
) = x
0
is denoted as
x(t).
Each component i of this bound can be calculated ac-
cording to the following equation
d
x
i
dt
= sup
u,x
1
,x
2
,...,x
i−1
,x
i+1
,...,x
n
f
i
(x
1
,x
2
,...,x
i−1
,
x
i
,x
i+1
,...,x
n
,u,t) , (27)
with the initial condition
x
i
(t
0
) = x
i,0
, where f
i
(·) is
the i-component of the vector-function f(·). The lower
bound x
i
(t) can be calculated in the same way by just
replacing sup by inf in (27).
Proof. The proof is a straightforward, however, it is
not presented in this paper. The reader can refer to
(Krotov et al., 1971) for an explicit proof.
Lemma 3.3. The upper bound for state variable n
1
(t)
is achieved with control input u(t) = 0.
Proof. Let us start with state variable n
12
(t). From
(2), it is clear that the second term in the right-hand
side is a non-positive and in particular it is equal to
zero for u(t) = 0. Therefore, the supremum of the
right-hand side will be achieved for u(t) = 0 and it
depends only on t. According to Lemma 3.2, an upper
bound
n
12
(t) is achieved with u(t) = 0. Now, let us
consider state variable n
1
(t). From (3) one can see
that the supremum over u(t) is achieved for u(t) =
0, then the right-hand side is a function of t and the
variables n
1
(t), n
12
(t). It has been shown that with
u(t) = 0 from (2) it follows that n
12
(t) =
n
12
(t). After
substitution n
12
(t) =
n
12
(t) in the right-hand side of
(3), it follows according to Lemma 3.2 that an upper
bound n
1
(t) = n
1
(t) is obtained for u(t) = 0.
Lemma 3.4. The lower bound for state variable n
1
(t)
is achieved with control input u(t) = 1.
Proof. The infimum over u(t) of the right-hand side
of (3) is achieved for u(t) = 1. Substituting u(t) = 1
into (3), one gets
dn
1
dt
= q
11
(t) + q
12
(t) − G
1
(n
1
(t)). (28)
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
18

It follows from Lemma 3.2 that the solution of (28) is
a lower bound n
1
(t).
Lemmas 3.3 and 3.4 complete the proof of The-
orem 3.1. One can add that if at some point in time
t = t
s
, the optimal trajectory will go left or right from
the value n
1
(t
s
) = n
∗
1
, then we can split the problem
into two pieces (namely from t = t
0
to t = t
s
and
from t = t
s
to t = t
f
) and build new upper or lower
bounds respectively from the initial point n
12
(t
s
) and
n
1
(t
s
) = n
∗
1
.
4 CONCLUSIONS
The analytical solution for the optimalperimeter feed-
back control with the maximum throughput criterion
in an urban region has been derived and described.
The modified Krotov-Bellman sufficient conditions of
optimality have been utilized for the proof of optimal-
ity. The resulting optimal control policy is oriented to
keep the state variable, i.e. the total number of the
moving vehicles in the region, as close as possible to
the critical accumulation, n
∗
1
, where the MFD value
is maximized. Though this optimal solution is in-
tuitively expected here it is rigorously proven. The
numerical simulations and comparison with existing
practices will be done in consequent papers.
ACKNOWLEDGEMENTS
This research was supported by Carl E. Schustak en-
ergy research and development fund.
REFERENCES
Aboudolas, K. and Geroliminis, N. (2013). Perimeter
and boundary flow control in multi-reservoir hetero-
geneous networks. Transportation Research Part B,
55:265–281.
Buisson, C. and Ladier, C. (2009). Exploring the impact of
homogeneity of traffic measurements on the existence
of macroscopic fundamental diagrams. Transporta-
tion Research Record, 2124:127–136.
Daganzo, C. F. (2007). Urban gridlock: Macroscopic mod-
eling and mitigation approaches. Transportation Re-
search Part B, 41(1):49–62.
Daganzo, C. F., Gayah, V. V., and Gonzales, E. J. (2011).
Macroscopic relations of urban traffic variables: Bi-
furcations, multivaluedness and instability. Trans-
portation Research Part B, 45(1):278–288.
Gayah, V. V. and Daganzo, C. F. (2011). Clockwise hystere-
sis loops in the macroscopic fundamental diagram: An
effect of network instability. Transportation Research
Part B, 45(4):643–655.
Geroliminis, N. and Boyacı, B. (2012). The effect of
variability of urban systems characteristics in the
network capacity. Transportation Research Part B,
46(10):1607–1623.
Geroliminis, N. and Daganzo, C. F. (2008). Existence
of urban-scale macroscopic fundamental diagrams:
some experimental findings. Transportation Research
Part B, 42(9):759–770.
Geroliminis, N., Haddad, J., and Ramezani, M. (2013). Op-
timal perimeter control for two urban regions with
macroscopic fundamental diagrams: A model pre-
dictive approach. IEEE Transactions on Intelligent
Transportation Systems, 14(1):348–359.
Geroliminis, N. and Sun, J. (2011a). Hysteresis phenomena
of a macroscopic fundamental diagram in freeway net-
works. Transportation Research Part A, 45(9):966–
979.
Geroliminis, N. and Sun, J. (2011b). Properties of a well-
defined macroscopic fundamental diagram for urban
traffic. Transportation Research Part B, 45(3):605–
617.
Godfrey, J. W. (1969). The mechanism of a road network.
Traffic Engineering and Control, 11(7):323–327.
Haddad, J. and Geroliminis, N. (2012). On the stability
of traffic perimeter control in two-region urban cities.
Transportation Research Part B, 46(1):1159–1176.
Haddad, J., Ramezani, M., and Geroliminis, N. (2013). Co-
operative traffic control of a mixed network with two
urban regions and a freeway. Transportation Research
Part B, 54:17–36.
Hajiahmadi, M., Haddad, J., Schutter, B. D., and Geroli-
minis, N. (2013). Optimal hybrid macroscopic traf-
fic control for urban regions: Perimeter and switching
signal plans controllers. In European Control Confer-
ence 13.
Ji, Y., Daamen, W., Hoogendoorn, S., Hoogendoorn-
Lanser, S., and Qian, X. (2010). Macroscopic funda-
mental diagram: Investigating its shape using simula-
tion data. Transportation Research Record, 2161:42–
48.
Ji, Y. and Geroliminis, N. (2012). On the spatial partition-
ing of urban transportation networks. Transportation
Research Part B, 46(10):1639–1656.
Keyvan-Ekbatani, M., Kouvelas, A., Papamichail, I., and
Papageorgiou, M. (2012). Exploiting the fundamnetal
diagram of urban networks for feedback-based gating.
Transportation Research Part B, 46(10):1393–1403.
Knoop, V., Hoogendoorn, S., and van Lint, H. (2013). The
impact of traffic dynamics on the macroscopic funda-
mental diagram. In 92nd Annual Meeting of Trans-
portation Research Board, Washington D.C., USA.
Knoop, V. L., Hoogendoorn, S. P., and Van Lint, J. W. C.
(2012). Routing strategies based on the macro-
scopic fundamental diagram. Transportation Re-
search Record, 2315:1–10.
Krotov, V. F. (1996). Global methods in optimal control
theory. M. Dekker, NY, USA.
OptimalFeedbackControlforaPerimeterTrafficFlowatanUrbanRegion
19

Krotov, V. K., Burkreev, V. Z., and Gurman, V. I. (1971).
New Variational Methods In Flight Dynamics. Coro-
net Books.
Mahmassani, H., Williams, J., and Herman, R. (1987). Per-
formance of urban traffic networks. In Gartner, N.
and Wilson, N., editors, Proceedings of the 10th In-
ternational Symposium on Transportation and Traffic
Theory, Amsterdam, The Netherlands. Elsevier.
Mahmassani, H. S., Saberi, M., and Zockaie, A. K.
(2013). Network gridlock: Theory, characteris-
tics, and dynamic. In Procedia - Social and
Behavioral Sciences, volume 80, pages 79–98.
doi: 10.1016/j.sbspro.2013.05.007 20th International
Symposium on Transportation and Traffic Theory.
Mazloumian, A., Geroliminis, N., and Helbing, D. (2010).
The spatial variability of vehicle densities as determi-
nant of urban network capacity. Philosophical Trans-
actions of the Royal Society A: Mathematical, Physi-
cal and Engineering Sciences, 368(1928):4627–4647.
Olszewski, P., Fan, H. S. L., and Tan, Y.-W. (1995). Area-
wide traffic speed-flow model for the Singapore CBD.
Transportation Research Part A, 29A(4):273–281.
Saberi, M. and Mahmassani, H. (2012). Exploring proper-
ties of network-wide flow-density relations in a free-
way network. In Transportation Research Board 91st
Annual Meeting, Washington, D.C.
Shraiber, A. and Haddad, J. (2014). Robust control design
for a perimeter traffic flow controller at an urban re-
gion. In European Control Conference 14 (Accepted).
Zhang, L., Garoni, T., and de Gier, J. (2013). A comparative
study of macroscopic fundamental diagrams of arte-
rial road networks governed by adaptive traffic signal
systems. Transportation Research Part B, 49:1–23.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
20
