Linear Switching System Identiﬁcation Applied to Blast Furnace Data

Amir H. Shirdel

, Kaj-Mikael Bjork

2,3

, Markus Holopainen

, Christer Carlsson

and Hannu T. Toivonen

Department of Chemical Engineering,

Abo Akademi University, Biskopsgatan 8, FIN-20500 Turku, Finland

Arcada University of Applied Sciences, FIN-00550 Helsinki, Finland

Institute of Advanced Management Systems Research,

Abo Akademi University, FIN-20520 Turku, Finland

Department of Information Technologies,

Abo Akademi University, Joukahaisenkatu 3-5 A, FIN-20520 Turku, Finland

Keywords:

System Identiﬁcation, Linear Switching System, Blast Furnace, ANFIS, Nonlinear System, Sparse Optimiza-

tion.

Abstract:

Switching systems are dynamical systems which can switch between a number of modes characterized by dif-

ferent dynamical behaviors. Several approaches have recently been presented for experimental identiﬁcation

of switching system, whereas studies on real-world applications have been scarce. This paper is focused on

applying switching system identiﬁcation to a blast furnace process. Speciﬁcally, the possibility of replacing

nonlinear complex system models with a number of simple linear models is investigated. Identiﬁcation of

switching systems consists of identifying both the individual dynamical behavior of model which describes

the system in the various modes, as well as the time instants when the mode changes have occurred. In this

contribution a switching system identiﬁcation method based on sparse optimization is used to construct linear

switching dynamic models to describe the nonlinear system. The results obtained for blast furnace data are

compared with a nonlinear model using Artiﬁcial Neural Fuzzy Inference System (ANFIS).

1 INTRODUCTION

An important goal of industries is to produce their

products with high quality and low costs. To reach

this goal, accurate models of industrial processes are

needed for monitoring and to maintain good quality

control. Data mining and modeling techniques can be

used to build predictive forecasting models, to ﬁnd

alternative actions to be taken, or simply to gain a

deeper understanding of the underlying inﬂuencing

elements.

Having more precise mathematical modes of in-

dustrial processes allow engineers to have better con-

trol of the processes to improve production and win

the competition in markets. One of the industries fac-

ing ﬁerce competition is the steel-making industry.

According to a review by the Association of Finnish

Steel and Metal Producers (Association of Finnish

Steel and Metal Producers, 2012), the ongoing polit-

ical and economic crisis in Europe has radically in-

creased price competition. In this paper, the blast fur-

nace for the steel making process is modeled. One

of the reasons which makes modeling of blast furnace

particularly complex is the fact that it is impossible to

directly observe the process inside the furnace. Op-

timization of this part is, however, essential for im-

provement in the overall process and quality of the

ﬁnal product. Because of the very high temperature

environment, embedding sensors for gathering data

is impossible. Therefore, it is treated as a black-box

system, relying on experienced engineers for process

monitoring and control.

System identiﬁcation can give mathematical mod-

els based on collected blast furnace data. The ﬁnal

goal of the study reported in this paper is to opti-

mize the blast furnace process and, more speciﬁcally

to consider the quality indicator which describes the

gas utilization rate in the furnace, using external sen-

sor data and other process information for its estima-

tion.

Steel plants use the processed iron which pro-

duced in blast furnaces by reducing oxygen from the

iron. The process is run continuously, with iron-

bearing materials and coke being charged from the

top of the furnace (Geerdes et al. 2009). During the

reduction process, two kind of reaction, direct and in-

direct, take place in the furnace. The direct one takes

place in the lower part of the furnace and depends on

643

H. Shirdel A., Björk K., Holopainen M., Carlsson C. and T. Toivonen H..

Linear Switching System Identiﬁcation Applied to Blast Furnace Data.

DOI: 10.5220/0005022806430648

In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 643-648

ISBN: 978-989-758-039-0

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

consumption of coke. The indirect one occurs in top

part, where the gas removes oxygen from the ore. The

efﬁciency of the indirect reaction is often expressed

as the gas utilization rate, which is considered as an

important performance indicator of the furnace. The

process is highly complex from a chemical point of

view as it involves numerous factors, nonlinear rela-

tions and a certain level of randomness.

There are not many researches on modeling blast

furnace dynamics due its highly complex behavior.

Mathematical models for describing the process have,

for instance, been proposed in (Nath, 2002) and (Dan-

loy et al. 2001). Linear data-driven models have

been studied in (Saxn and stermark, 1996), (Korpi

et al. 2003) and (Bhattacharya, 2005). Nonlinear

soft computing techniques have been applied to blast

furnace process modeling in, among other: (Hao,

2004), (Helle and Saxn, 2005) and (Pettersson et al.

2007). A novel approach is presented in (Agarwal

et al. 2010) where they train a neural network us-

ing multi-objective genetic algorithms based on car-

bon dioxide content of top gas and silicon content in

the hot metal output. In (Bjork et al. 2013), AN-

FIS allows for customization regarding membership

functions, inputs and rules, an appropriate degree of

complexity is expected to be found.

Nonlinear systems with several operating regimes

can be modeled as switching systems, which switch

between a number of operational modes associated

with the various operating conditions. In this case

the mode is usually known or is a function of known

variables. In more general cases, the mode switches

may be random, or they may depend on variables

which are unknown. In this paper, a switching system

model is identiﬁed to estimate the gas utilization rate

of a blast furnace from available sensor data. Follow-

ing (Shirdel et al. 2014), the identiﬁcation problem

is posed as a support vector regression (SVR) prob-

lem, and the models associated with the various op-

erational modes are found by solving a sequence of

sparse optimization problems techniques. The pre-

diction performance of the identiﬁed switching sys-

tem models of the blast furnace are compared with

results obtained with models constructed using Artiﬁ-

cial Neural Fuzzy Inference Systems (ANFIS).

2 SWITCHING SYSTEM

IDENTIFICATION

Hybrid systems are a kind of switching systems char-

acterized by a logical dynamical component, which

determines the mode switches, and a continuous dy-

namical component, which determines the system be-

havior in the various operational modes. Hybrid sys-

tems can be categorized into ﬁve classes (Heemels

et al. 2001). Piece-wise afﬁne (PWA) systems are

a class of hybrid systems whose state input domain

is partitioned into a ﬁnite number of non-overlapping

convex polyhedral regions, with linear or afﬁne sub-

systems in each region (Sontag, 1981).Piece-wise-

linear functions are universal approximation of mul-

tivariate functions (Lin and Unbehauen, 1992). Due

to their approximate features, piece-wise afﬁne hybrid

systems are useful for nonlinear system identiﬁcation.

One approach to black-box identiﬁcation of non-

linear dynamical systems using experimental process

input-output data is to identify a linear switching sys-

tem which describes the data. A special problem

in switching system identiﬁcation is the fact that the

times of the mode switches may not be known. In

these cases the switching times between the vari-

ous modes should be identiﬁed simultaneously with

the individual models, which make the identiﬁcation

of switching systems signiﬁcantly more demanding

than standard system identiﬁcation. Therefore, in

many studies of switching system identiﬁcation var-

ious simplifying assumptions have been made.

In order to cope with the challenging problem of

simultaneous identiﬁcation of system modes and pa-

rameters, a number of techniques have been devel-

oped (Saad et al. 2007), (Aliev et al. 2004). Segmen-

tation of time-varying systems and signals has been

discussed in (Ohlsson et al. 2010). Sparse optimiza-

tion which is based on ﬁnding each model sequen-

tially is proposed in (Bako, 2011). In (Shirdel et al.

2014), a method based on support vector regression

and sparse optimization techniques was proposed for

identiﬁcation of switching systems. Recently in (Le

et al. 2013), an approach to identify hybrid systems

with unknown nonlinearities in the sub-models using

combination of sparse optimization and support vec-

tor machines was presented.

In this paper we consider a switching system de-

scribed by the time-varying linear model

y(k) = ϕ(k)

θ(k) + e(k) (1)

where y(k) is the output, e(k) is a disturbance, and

ϕ(k) is a state vector. The state vector consists of the

variables used to predict the output y(k). For exam-

ple, for autoregressive with exogenous terms (ARX)

mode, the state vector takes the form

ϕ(k)

= [y(k − 1), ..., y(k − r), u(k), ..., u(k − r)]

where u(k) is the exogenous input to the system.

It is assumed that the system dynamics switch be-

tween a number of modes, so that

θ(k) ∈

{

, θ

, . . . , θ

}

(2)

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

644

where θ

is the vector of system parameters in the ith

mode, and M is the number of modes.

The switching system identiﬁcation problem con-

sists of ﬁnding estimates of the parameter vec-

tors θ

from empirical process data {y(k), ϕ(k), k =

1, 2, . . . , N}. Notably, it is not assumed that the time

instants when the various modes have been active

are known. This implies that the identiﬁcation is

essentially identical to a combinatorial optimization

problem. Although such problems are usually in-

tractable, the switching system identiﬁcation problem

can often be solved with a high degree of accuracy

or even exactly via a sparse optimization formulation

and l

-relaxation (Bako, 2011), (Shirdel et al. 2014),

(Lughofer and Kindermann, 2010).

The approach used in this paper is based on the

fact that if mode i has been active at N

time instants,

then, assuming that e(k) ≤ ε, the inequality



y(k) − ϕ(k)



≤ ε (3)

holds at these N

time instants. It follows that the

most commonly occurring mode and the associated

parameters θ

can be determined by ﬁnding the pa-

rameter vector

such that the number N

of time

instants for which the inequality (3) holds is max-

imized. This is a combinatorial optimization prob-

lem, which can be addressed using sparse optimiza-

tion techniques (Bako, 2011).

In (Shirdel et al. 2014), an approach was proposed

using the observation that the constraints (3) are iden-

tical with the ε-insensitive cost used in support vector

regression. The system parameters associated with a

given mode can then be found by solving the opti-

mization problem (Shirdel et al. 2014)

Minimize

θ,ξ

,ξ

−

θk

∑

k=1

(ξ

+ ξ

−

) (4)

subject to the ε-insensitive constraints

y(k) − ϕ(k)

θ ≤ ε + ξ

−y(k) +ϕ(k)

θ ≤ ε + ξ

−

(5)

, ξ

−

≥ 0

Here p = 1 or 2, corresponding to a linear or, re-

spectively, quadratic programming problem and C

trade off weight.

The problem of ﬁnding the mode which has been

active at the maximum number of time instants corre-

sponds to ﬁnding the parameters θ such that the max-

imum number of variables ξ

, ξ

−

are zero. This is

a sparse optimization problem, for which the second

term in (4) provides an l

-relaxation, and by iterative

reweighting applied to the weights C

the problem can

in many cases be solved with a high degree of accu-

racy (Bako, 2011), (Shirdel et al. 2014). In this way

the various system modes and the associated param-

eter vectors can be computed one by one. We have

the following algorithm (Bako, 2011), (Shirdel et al.

2014).

Algorithm. Identiﬁcation of switching system.

Step 1. Initialization: set i = 1.

Step 2. Solve the SVR problem deﬁned by (4), (5)

using iterative reweighting of C

to ﬁnd a sparse so-

lution in the variables ξ

, ξ

−

. The solution gives a

parameter estimate

for mode i. Remove the data

pairs (ϕ(k), y(k)) at which mode i has been active.

Step 3. Check the reduced data set for convergence:

if all data pairs have been accounted for, stop. Other-

wise, set i := i +1 and continue from step 2 using the

reduced data set.

3 IDENTIFICATION OF BLAST

FURNACE

In this section the switching system identiﬁcation

methods described in section 2 is applied to blast fur-

nace data. The goal of the model is to predict the gas

utilization as described by the carbon dioxide con-

tent of top gas as a function of measured variables

received from sensor data.

Table 1: Inputs.

Input No. Description

1 Pellets+sinter by total

2 Coke by total

3 Iron by total

4 Pellets+sinter by volume

5 GAS temp PCA

6 GAS temp PCA

7 GAS temp PCA

8 Burden height

9 Blast volume

10 Pressure by volume

11 Oxygen in blast

12 Hydrogen in top gas

13 Oil by blast volume

3.1 The Blast Furnace Data

In a complex plant like blast furnace, much redundant

affection can inﬂuence our major part of identiﬁcation

which is measured data. For this study, three months

of detailed operational blast furnace data was used

for training. The ﬁnal set of preprocessed data con-

sisted of data collected from 2208 hours of furnace

LinearSwitchingSystemIdentificationAppliedtoBlastFurnaceData

645

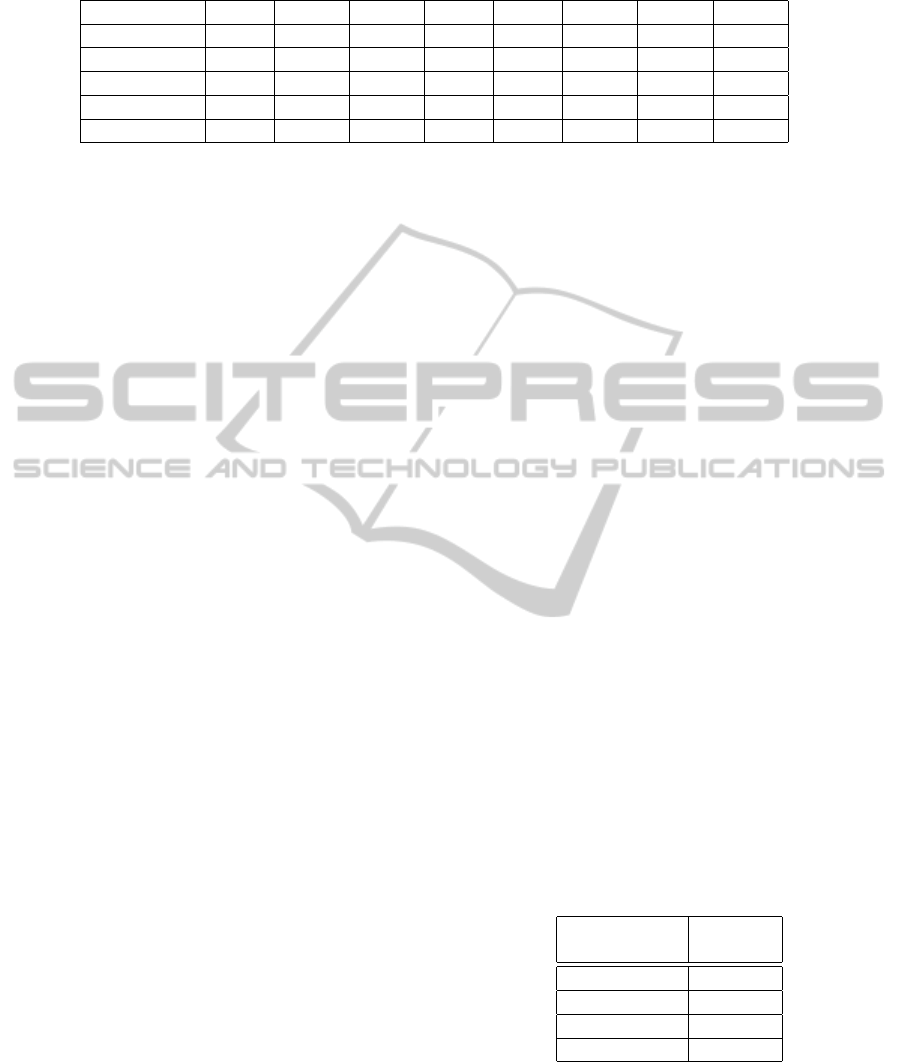
Table 2: Estimated parameters b

(i)

1,l

for input u

for various time lags l when using M = 4 modes.

Time lag 1 2 3 4 5 6 7 8

Input No. 1

Subsystem 1 0.000 0.000 0.979 1.075 0.000 -0.815 0.000 0.000

Subsystem 2 0.000 0.000 -0.623 0.000 0.564 0.000 0.816 -0.159

Subsystem 3 0.000 -1.854 0.000 0.000 0.000 0.000 0.000 0.000

Subsystem 4 0.000 0.000 -0.193 0.000 0.000 0.000 -0.396 0.147

operation. After consulting experts, it turned out that

many points of data are not sufﬁciently reliable and

should be removed. The ﬁnal number of data points

was therefore 1800.

One of the most important performance indica-

tors of blast furnace is measuring the ratio of carbon

monoxide converted to carbon dioxide. This indicator

was chosen as the target series for the conducted anal-

ysis and modeling. It evaluates performance of the

data understanding indirect reduction reaction taking

place in the upper part of the furnace and controlling

this process by injecting oxygen, can allow furnace to

burn less coke and cost saving.

3.2 The Inputs

Input data entails charging data which are precise

amounts of burden materials and coke charged into

the furnace per time unit, continuous process data

from external sensors and data from analysis of hot

metal and some other variables. Top-gas exiting the

furnace can be considered as an input series. A

discussion of the role of hydrogen competing with

carbon monoxide in reducing oxygen is given in

(Geerdes et al. 2009). The inputs which are used in

the modeling of the blast furnace are shown in Table

The output y(k) (carbon dioxide content of top

gas) was modeled as function of the input variables

(k) in Table 1. The model structure was

y(k) =

∑

j=1

j,1

(k)u

(k − 1) + ··· + b

j,13

(k)u

(k − 13)

where the parameters b

j,l

(k) ∈ {b

(1)

j,l

(2)

j,l

, . . . , b

(M)

j,l

}

belong to the set (2) associated with the system

modes.

Each input variable affect the process with a time

lag. Some of the variables affect the process rapidly,

such top gas-related variables, and some others have

a slower effect, like charging data. In the identiﬁca-

tion method used here, the time lags of the various

process inputs were obtained as part of the identiﬁ-

cation process, as the ﬁrst term of the cost function

(4) forces parameter which do not affect the output to

zero, cf. (Shirdel et al. 2014), where the approach was

used to identify systems of unknown dimensions. Es-

timated time lags and parameters for modeling with

M = 4 subsystems for ﬁrst input are shown in Table

2. It is seen that the time lag of the input is different

for different subsystems.

4 RESULTS

In this section, modeling by using the linear switch-

ing system identiﬁcation approach is conducted. The

required data was taken from input series based on the

consultation of expert (Table 1). The maximum time

lag that we allowed our approach to have in this blast

furnace system is 8.

The result of each identiﬁed linear switching sys-

tem is given based on root mean square (RMS) error

between the estimated output and real output in Table

3. For comparison, the error of ANFIS model output

(Bjork et al. 2013) is shown in Table 4. It is seen that

the switching system model is slightly more accurate

than ANFIS model. A major difference is that in con-

trast to the approach considered here, in the ANFIS

modeling studied in (Bjork et al. 2013) it was not

possible to ﬁnd the optimal time lags, or to include

all 13 input variables in the model due to a too heavy

computational burden. The output of a switching sys-

tem model is illustrated in Fig. 2, the mode switches

of a system with four modes are shown in Fig. 1.

Table 3: Root mean square error of estimated output of us-

ing identiﬁed switching system models.

Subsystem of

modes

RMSE

1 0.0840

4 0.0571

6 0.0537

8 0.0516

5 CONCLUSION AND

DISCUSSION

One application of switching system models is to rep-

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

646

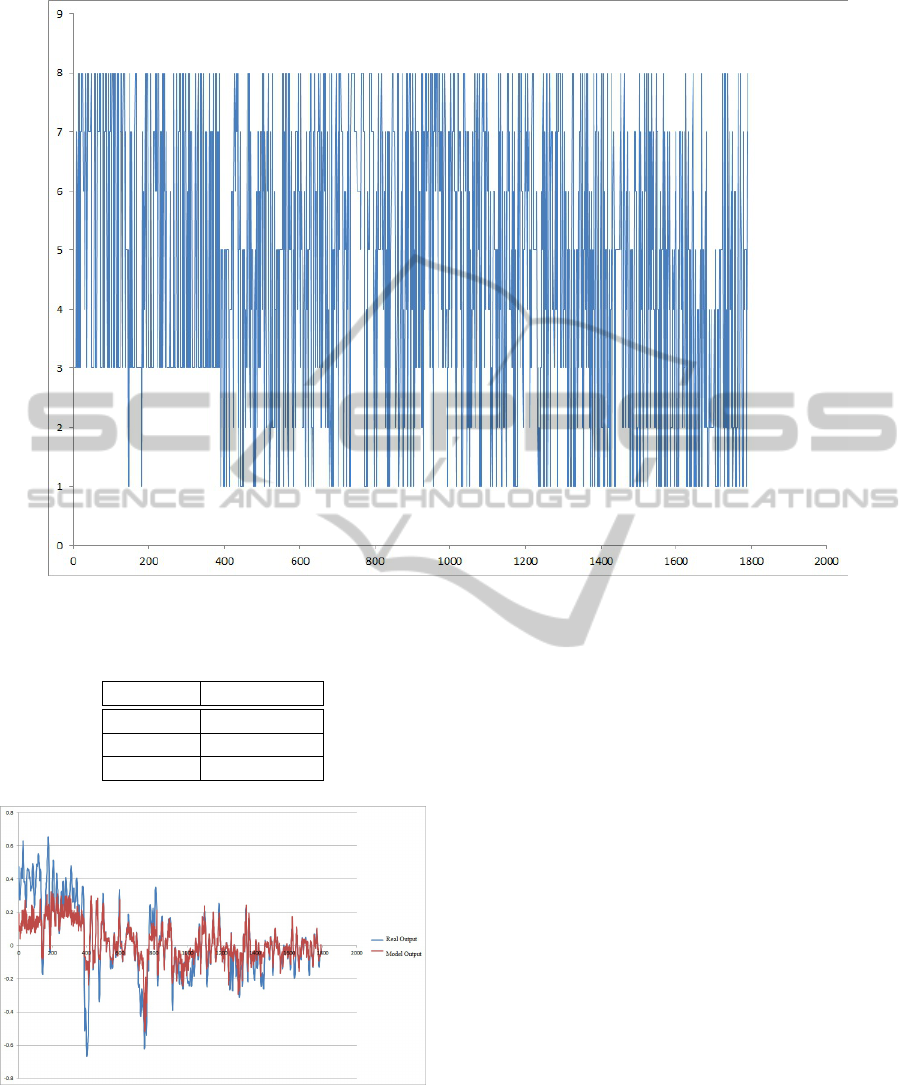
Figure 1: Mode switches of system with eight modes.

Table 4: Root mean square error of estimated output using

ANFIS model.

RMSE Input set

0.054 1,5,10,12,13

0.052 6,7,10,12,13

0.056 1,6,7,10,13

Figure 2: Normalized process output and model output

when using linear switching system with M = 8 modes.

resent complex systems with a number of simple lin-

ear subsystems. In this study, a switching system

model of a blast furnace process was identiﬁed from

experimental process data. The results show that with

a relatively few linear systems, quite good models can

be obtained, and by allowing more subsystems, the

nonlinearities are captured, even so that output is pre-

dicted slightly better than with the ANFIS method,

cf. Tables 3 and 4.

In future work, we will generalize the approach to

nonlinear switching systems for improved accuracy,

and also to test the method to other industrial pro-

cesses.

ACKNOWLEDGEMENTS

This work has been funded by the Foundation of bo

Akademi University and the center for optimization

and Systems Engineering at bo Akademi as well as

IAMSR at bo Akademi and the TUF foundation at

Arcada University of Applied Sciences.

REFERENCES

Bjork, K-M., Holopainen, M., Wikstrm, R., Saxen, H.,

Carlsson, C., Sihvonen, M.: Analysis of Blast Fur-

nace Time Series Data with ANFIS. TUCS Technical

Report 1094 ISBN 978-952-12-2986-2 (2013)

LinearSwitchingSystemIdentificationAppliedtoBlastFurnaceData

647

Shirdel, A. H., Bjork, K-M., Toivonen, H. T.: Identiﬁca-

tion of Linear Switching System with Unknown Di-

mensions. In: 47 Hawaii International Conference on

System Sciences, HICSS-47 (2014)

The Association of Finnish Steel and Metal Pro-

ducers, Structure Review of Metal Reﬁnement

(2012), http://www.teknologiateollisuus.ﬁ/ﬁle/14190/

MJ rakennekatsaus212.pdf.html

Geerdes, M., Toxopeus, H. L., Van der Vliet, C.,

Chaigneau, R., Vander, T.: Modern Blast Furnace

Ironmaking: An Introduction. Ios PressInc, ISBN

9781607500407(2009)

Nath, N. K.: Simulation of gas ﬂow in blast fur-

nace for different burden distribution and cohesive

zone shape. Materials and Manufacturing Processes,

17(5):671681 (2002). doi: 10.1081/AMP-120016090

Danloy, J., Mignon, R., Munnix, G., Dauwels, L., Bonte, L.:

A blast furnace model to optimize the burden distri-

bution. In: 60th Ironmaking Conference Proceedings,

pages 3748, Baltimore (2001)

Yu, Y., Saxn, H.: Experimental and dem study

of segregation of ternary size particles in a

blast furnace top bunker model. Chemical En-

gineering Science, 65(18):52375250 (2010). doi:

10.1016/j.ces.2010.06.025

Agarwal, A., Tewary, U., Petterson, F., Das, S.,

Saxn, H., Chakraborti,N.: Analysing blast fur-

nace data using evolutionary neural network

and multiobjective genetic algorithms. Ironmak-

ing and Steelmaking, 37(5):353359 (2010). doi:

10.1179/030192310X12683075004672

Saxn, H., stermark, R.: Varmax-modelling of blast furnace

process variables. European Journal of Operational

Research, 90(1):85101 (1996). doi: 10.1016/0377-

2217(94) 00304- 1

Korpi, M., Toivonen, H., Saxn,B.: Modelling and identiﬁca-

tion of the feed preparation process of a copper ﬂash

smelter. Computer Aided Chemical Engineering, El-

sevier (2003),(14):731-736, ISSN 1570-7946, ISBN

9780444513687

Bhattacharya, T.: Prediction of silicon content in blast fur-

nace hot metal using partial least squares (pls). ISIJ

International, 45(12):19431945, (2005)

Hao, X., Zheng, P., Xie, Z., Du, G., Shen, F.: A predic-

tive modeling for blast furnace by integrating neu-

ral network with partial least squares regression. In:

IEEE International Conference on industrial tech-

nology, volume 3, pages 11621167 Vol. 3,106-107

(2004). doi: 10.1109/ICIT.2004.1490724

Helle, M., Saxn, H.: A method for detecting cause-effects in

data from complex processes. In: Proceedings of the

International Conference in Coimbra, Pages 104107,

Portugal (2005)

Pettersson, F., Chakraborti, N., Saxn, H.: A genetic algo-

rithm based multi-objective neural net applied to noisy

blast furnace data. Applied Soft Computing, Volume

7, Issue 1, January 2007, Pages 387397

Heemels, W.P.M.H., De Schutter, B., Bemporad, A.: Equiv-

alence of hybrid dynamical models. Automatica, vol.

37, no. 7, pp. 10851091, (2001)

Sontag, E. D.: Nonlinear regulation: The piecewise linear

approach. IEEE Trans. Automatic Control, vol. 26, no.

2, pp. 346358, (1981)

Lin, J. N., Unbehauen, R.: Canonical Piecewise-linear

Approximations. IEEE Trans. Circuits Systems I-

Fundamental Theory and Applications, vol. 39, no. 8,

pp. 697699, (1992)

Saad, A., Avineri, E., Dahal, K., Sarfraz, M.: Soft Comput-

ing in Industrial Applications, Springer (2007)

Aliev, R. A., Fazlollahi, B, Aliev, R. R.: Soft Comput-

ing and Its Applications in Business and Economics,

Springer, edition 5 (2004)

Ohlsson, H.,Ljung, L., Boyd, S.: Segmentation of ARX-

models using sum-of-norms regularization. Automat-

ica, vol. 46, pp. 1107-1111 (2010)

Bako, L.: Identiﬁcation of switched linear systems via

sparse optimization. Automatica, vol. 47, pp. 668-677

(2011)

Le, V. L., Lauer, F., Bako, L., Bloch. G.: Learning nonlin-

ear hybrid systems: from sparse optimization to sup-

port vector regression. In: HSCC - 16th ACM Inter-

national Conference on Hybrid systems: Computation

and Control - 33-42 (2013)

Lughofer, E. and Kindermann, S. (2010). SparseFIS: Data-

driven learning of fuzzy systems with sparsity con-

straints. Fuzzy Systems, IEEE Transactions on, 18(2),

396-411.

ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics

648