
A Hybrid Approach for Content Based Image Authentication
Jinse Shin and Christoph Ruland
Chair for Data Communications Systems, University of Siegen, Hoelderlinstr. 3, Siegen, Germany
Keywords:
Content based Image Authentication, Perceptual Image Hashing, Tamper Detection.
Abstract:
Perceptual image hashing has received an increased attention as one of the most important components for
content based image authentication in recent years. Content based image authentication using perceptual
image hashing is mainly classified into four different categories according to the feature extraction scheme.
However, all the recently published literature that belongs to the individual category has its own strengths and
weaknesses related to the feature extraction scheme. In this regard, this paper proposes a hybrid approach to
improve the performance by combining two different categories: low-level image representation and coarse
image representation. The proposed method employs a well-known local feature descriptor, the so-called His-
togram of Oriented Gradients (HOG), as the feature extraction scheme in conjunction with Image Intensity
Random Transformation (IIRT), Successive Mean Quantization Transform (SMQT), and bit-level permuta-
tion to construct a secure and robust hash value. To enhance the proposed method, a Key Derivation Function
(KDF) and Error Correction Code (ECC) are applied to generate a stable subkey based on the coarse im-
age representation. The derived subkey is utilized as a random seed in IIRT and HOG feature computation.
Additionally, the experimental results are presented and compared with two existing algorithms in terms of
robustness, discriminability, and security.
1 INTRODUCTION
The advances in electronic devices, wireless mobile
communication, and multimedia technologies have
accelerated the explosive growth of multimedia traf-
fic, so that the needs of a secure multimedia com-
munication over wireless channels have been raised.
However, the emerging security demands are difficult
to be met by the standardized cryptographic methods
(ISO/IEC9797, 2011; NIST-FIPS, 2013) or soft au-
thentication methods (Graveman and Fu, 1999; Bon-
celet, 2006; Ur-Rehman and Zivic, 2013) since the
security requirements of multimedia communication
are different in many ways from those of the tradi-
tional data communication (Shin and Ruland, 2013).
The main difference from the security perspective
is the definition of data integrity. The general def-
inition of data integrity is to assure the binary rep-
resentation of data has not been corrupted or modi-
fied during a data communication procedure, whereas
data integrity in multimedia communication requires
ensuring the perceptual content has not been manip-
ulated even though its binary representation is com-
pletely different. For this reason, content based mul-
timedia authentication approach has been considered
as an attractive solution.
In this regard, perceptual image hashing has re-
ceived an increased attention to authenticate the im-
age content on a semantic level. There have been pro-
posed several image authentication schemes based on
the perceptual image hashing in the literature (Han
and Chu, 2010; Haouzia and Noumeir, 2008). Ac-
cording to the type of feature extraction scheme, con-
tent based image authentication is largely classified
into four different categories: Image statistics, rela-
tion, coarse image representation, and low-level im-
age representation based feature extraction (Monga
and Evans, 2006).
Although all the recently published literature
within those categories can achieve good performance
with respect to robustness against content preserving
modifications, they possess their own limitations re-
lated to the feature extraction scheme. Thus, this pa-
per proposes to combine two different types of fea-
ture extraction scheme: low-level image represen-
tation and coarse image representation. As a low-
level image representation based feature extraction
scheme, HOG feature descriptor is employed with
IIRT, SMQT, and bit-level permutation not only to
capture the local characteristics of an image but also
371
Shin J. and Ruland C..
A Hybrid Approach for Content Based Image Authentication.
DOI: 10.5220/0005059003710378
In Proceedings of the 11th International Conference on Security and Cryptography (SECRYPT-2014), pages 371-378
ISBN: 978-989-758-045-1
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

to construct a secure and robust hash. Likewise, a
coarse image representation computed by the use of
Discrete Cosine Transform (DCT) jointly with Sin-
gular Value Decomposition (SVD) is utilized to pro-
duce a subkey in conjunction with KDF and ECC.
The derived subkey can be used as a random seed
of the pseudorandom number generator used for IIRT
and HOG feature computation to enhance the discrim-
inability and security of the proposed method.
The rest of this paper is organized as follows. Sec-
tion 2 briefly introduces some of the representativeal-
gorithms within each category and explains their se-
curity related issues. Section 3 presents the proposed
method for content based image authentication using
a hybrid approach, followed by experimental results
with a discussion in section 4. Finally, the last section
concludes the paper with a brief summary.
2 PRIOR WORKS
The basic idea behind content based image authen-
tication approach is that it can be aware of the im-
age content by constructing an image hash value from
the invariant image features, and then generate a Mes-
sage Authentication Code (MAC) or digital signature
from it. Consequently, the feature extraction scheme
affects the performance in terms of robustness and
discriminability since the extracted features play a
main role to distinguish between the malicious ma-
nipulations and acceptable content preserving modifi-
cations. Some representative algorithms of each cate-
gory are reviewed in this section.
The approach using the image statistics based fea-
ture extraction computes the statistics of an input im-
age such as mean, variance, and higher moments of
intensity values as an invariant feature. (Venkate-
san et al., 2000) proposed to utilize the statistics of
Discrete Wavelet Transform (DWT) coefficients cal-
culated from the randomly partitioned rectangles of
each sub-band in wavelet decomposition of an im-
age. Another scheme is approximate Image Mes-
sage Authentication Code (IMAC) proposed by (Xie
et al., 2001), which applies a cryptographic primitive
Approximate Message Authentication Code (AMAC)
(Graveman and Fu, 1999) on the most significant bits
of 8×8 block average with image histogram enhance-
ment. Although those schemes demonstrate good ro-
bustness against several content preserving modifica-
tions, they possess the limitation that an image can be
easily modified without altering its image statistics.
The relation based approach exploits the invariant
relationship between a pair of transform coefficients.
As a representative scheme of this category, (Lin and
Chang, 2001) proposed a robust image authentication
method using the relationship between DCT coeffi-
cients at the same position in separate blocks of an
image. Since this invariant property is derived from
the fact that all DCT coefficients at the same position
in DCT blocks are divided by the same quantization
table during JPEG lossy compression process, it can
achieve excellent robustness against JPEG compres-
sion. However, most of the AC coefficients in DCT
block where the image has a smooth texture may be-
come zero after JPEG lossy compression, so that the
extracted features cannot be reliable for image au-
thentication any more.
The approach based on the coarse image represen-
tation utilizes the invariance in the transform domain,
which may preserve the significant characteristics of
the image. (Mihcak and Venkatesan, 2001) applied a
simple iterative filtering operation on the binary map
of the DWT approximation sub-band to obtain the ge-
ometrically strong components. (Kozat et al., 2004)
proposed another interesting image hashing algorithm
which applies SVD to pseudo-randomly chosen semi-
global regions of an image, then selects the strongest
singular vectors to extract robust features. Compared
to the other categories, this approach obtains better
robustness under acceptable modifications. However,
such an excellent robustness may lead to a false posi-
tive authentication with a high probability. Moreover,
the iteration of their algorithms to capture the signifi-
cant characteristics of an image requires a high com-
putational complexity.
The low-level image representation based ap-
proach uses low-level image features such as edges
or feature points, which are widely used for ob-
ject or scene recognition in image processing do-
main. (Queluz, 1998) proposed an image authenti-
cation scheme that relies on image edges obtained by
Sobel or Canny edge detector, whereas (Monga and
Evans, 2006) proposed to extract visually significant
image feature points by using end-stopped wavelet
based feature detection algorithm. The main prob-
lem of the low-level image representation is that edges
or feature points can be easily distorted by the quan-
tization errors and other compression artifacts even
though they are good at capturing the local character-
istics of an image. In particular, the algorithms using
feature points may not be able to detect the malicious
manipulations since they select and use only the lim-
ited number of feature points retaining the strongest
coefficients to construct an image hash. Accordingly,
it is highly possible to add or remove a set of feature
points for malicious manipulations while maintaining
the same strongest feature points of an image (Hsu
et al., 2009).
SECRYPT2014-InternationalConferenceonSecurityandCryptography
372
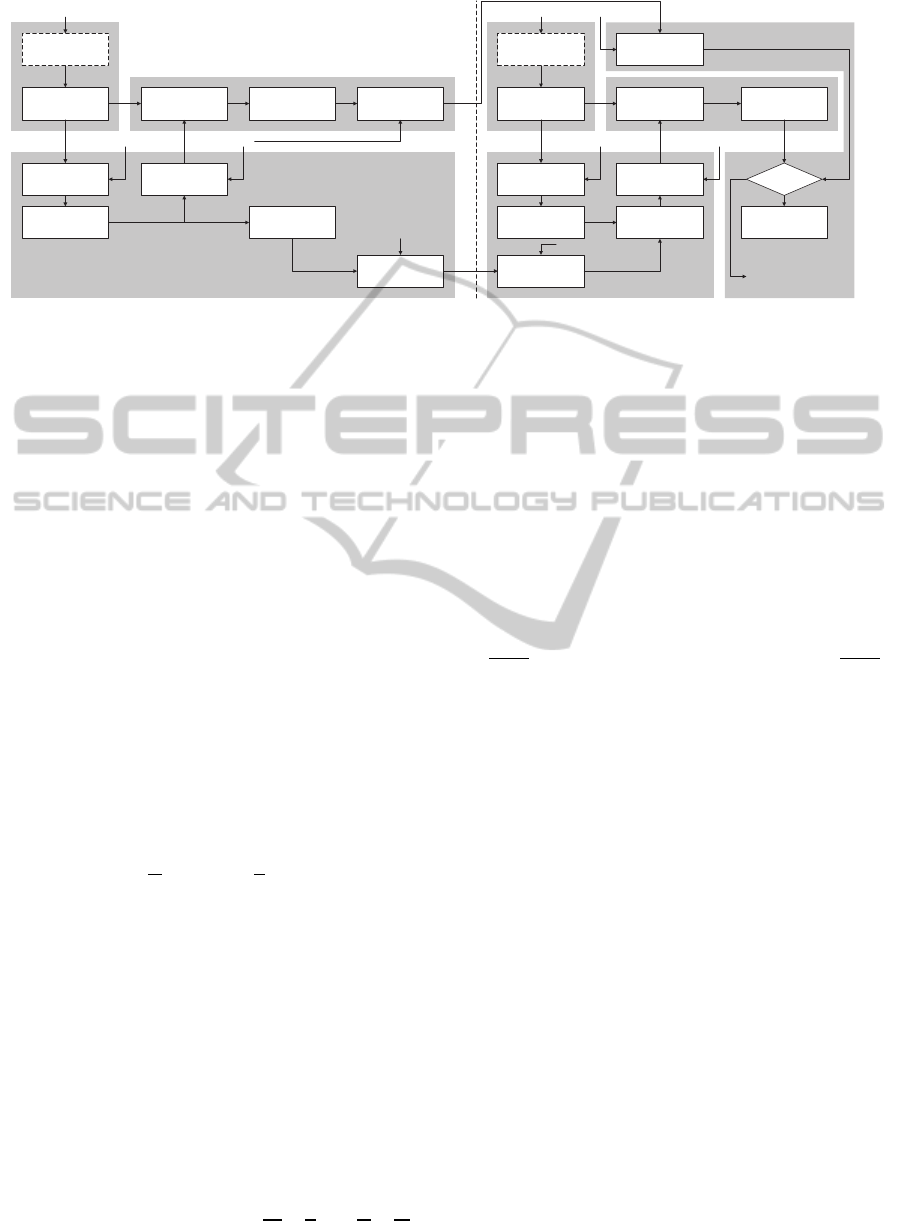
Horizontal / Vertical
block partitioning
Low-pass filtering
Downsampling /
Block permutation
DCT-SVD computation Error correction encoding
HOG computation with
image intensity random
transform
Successive Mean
Quantization Transform
Bit-level permutation
Symmetric encryption
enc(PC, Km)
Subkey Derivation
kdf(Km, Si)
TAGIH
TAGPC
Km
Input image (I)
KmKm
Horizontal / Vertical
block partitioning
Low-pass filtering
Downsampling /
Block permutation
DCT-SVD computation Error correction decoding
HOG computation with
image intensity random
transform
Successive Mean
Quantization Transform
Subkey Derivation
kdf(Km, CSi)
Ki’
Received image (I’)
Km
Km
Symmetric decryption
dec(TAGpc, Kpr)
Inverse permutation
Distance < T
Tamper detection &
Localization
No
Authentic
Yes
Salt (CSi)
Km
Km
Parity Code (PC)
Image Hash Generation using HOG feature descriptor Image Hash Generation using HOG feature descriptor
Sub-key Derivation using the coarse image representation (DCT-SVD)
Sub-key Derivation using the
coarse image representation (DCT-SVD)
Hash Verification, Tamper detection,
and Localization
Parity Code
(PC)
Ki
Hash generation procedure Hash verification procedure
Salt (Si)
Preprocessing Preprocessing
Si’
Figure 1: Block diagram of the proposed method.
3 PROPOSED METHOD
A hybrid method proposed in this paper is based on
two main ideas: (a) HOG feature descriptor from
a randomly transformed image by IIRT, (b) Subkey
derivation from the coarse image representation in
conjunction with ECC. Fig. 1 illustrates a block dia-
gram of the proposed method, and the following sub-
sections introduce each step of the hash generation
and verification procedure.
3.1 Hash Generation Procedure
3.1.1 Preprocessing
A low-pass filtering can be optionally applied on an
image to reduce the noise as a preprocessing oper-
ation. After that, the smoothed image is horizon-
tally and vertically partitioned into a total of (r + c)
non-overlapped blocks, H
i
(1 ≤ i ≤ r) and V
j
(1 ≤
j ≤ c) with the size of M
′
× N and M × N
′
respec-
tively, where M
′
=
M
r
and N
′
=
N
c
when the dimen-
sion of an input image is M × N. Accordingly, all
the blocks of an input image are represented by I =
{B
1
, ..., B
r+c
} = {H
1
, ..., H
r
, V
1
, ..., V
c
}.
3.1.2 Subkey Derivation
As a coarse image representation based feature ex-
traction scheme, DCT-SVD hashing algorithm that
demonstrates an excellent robustness is used with a
slight modification (Kozat et al., 2004). The sub-
key derivation process using the modified DCT-SVD
hashing scheme is described as follows.
(1) Perform downsampling on all the blocks B
i
to
halve the spatial dimension of an image. The di-
mension of downsampled B
i
is
M
′
2
×
N
2
and
M
2
×
N
′
2
for the horizontal and vertical block respectively.
(2) Perform a sub-block permutation for each B
i
after
splitting the downsampled B
i
into non-overlapped
p× p sub-blocks. Let BP
i
be the permuted block
of the downsampled B
i
.
(3) Compute 2D DCT for each block of d × d within
BP
i
, then take only the DC coefficient from them.
DC
i
for each BP
i
is constructed by concatenat-
ing all the DC coefficients of all d × d DCT
blocks within BP
i
, and represented as DC
i
=
DC
i,1
, ..., DC
i, j
. DC
i, j
denotes the DC coeffi-
cient of j-th DCT block within BP
i
, where 1≤ j ≤
M
′
×N
(2d)
2
for the horizontal block and 1 ≤ j ≤
M× N
′
(2d)
2
for the vertical block.
(4) Apply SVD on DC
i
and take the strongest singular
vectors. The final coarse image representation S
i
from each B
i
is constructed by converting the vec-
tors into the integer between 0 and 2
q
− 1, where
q is the number of quantization bits.
(5) Given the final coarse image representation S
i
acts
as a non-secret parameter called ‘salt’ in KDF for
B
i
. Hence, a subkey K
i
for each B
i
is derived by
K
i
= kd f (K
m
, S
i
), where kd f (·, ·) is a key deriva-
tion function with a master secret key K
m
and salt
S
i
. Note that the proposed method does not de-
pend on any specific type of KDF algorithms so
that any standardized KDF can be adopted in the
proposed method (NIST-SP, 2009; Krawczyk and
Eronen, 2010).
(6) For the purpose of increasing robustness, convert
S
i
into a Gray code and encode each vector el-
ement within S
i
using ECC to obtain the parity
code bits PC
i
. Note that the proposed method
applies the Hamming code (n, k) that can cor-
rect single-bit errors, where n and k represent the
length of output encoded message and original
message respectively.
AHybridApproachforContentBasedImageAuthentication
373

(7) Concatenate all the parity code bits of every S
i
to construct PC = {PC
1
, ..., PC
r+c
}. The final
tag information concerning the parity code bits
can be obtained by TAG
PC
= enc(K
m
, PC), where
enc(·, ·) denotes a symmetric encryption function.
As long as the coarse image representation S
i
ex-
tracted in step (4) can be invariant under a certain
level of distortions, KDF can produce the same sub-
key for each B
i
in step (5) since S
i
is utilized as a salt
value in KDF. In this context, the proposed method
employs Gray code conversion and Hamming error
correction code in step (6) to obtain the stable salt
value by correcting single-bit errors. Due to the lo-
cality of the distortion introduced by malicious ma-
nipulations, it is expected that the hamming distance
between the coarse image representations in the Gray
code is larger than one when the image is tampered.
In this manner, S
i
computed from the tampered im-
age cannot be corrected whereas the one from accept-
able modifications can be corrected. Thus, the use of
single error correcting codes is much preferable than
burst error correcting codes in the proposed method.
3.1.3 Image Hash Generation
HOG feature descriptor may make a false authentica-
tion decision when it is used for content based image
authentication, since the image gradients can be dis-
torted by the quantization errors and other compres-
sion artifacts. To cope with this problem, a method to
randomly transform the image intensity before HOG
computation is proposed in this paper. The followings
present how to generate a final hash value using HOG
feature descriptor.
(1) Apply IIRT given by equation (1) on every B
i
, re-
sulting in the randomly transformed image BT
i
.
BT
i
(x, y) = B
i
γ
(x, y) + rand
x,y
(K
i
, r
max
) (1)
B
i
(x, y) and BT
i
(x, y) respectively represent the
pixel intensity at the coordinate (x, y) in each
block of B
i
and BT
i
, where 1 ≤ x ≤ M
′
, 1 ≤ y ≤ N
for the horizontal block and 1 ≤ x ≤ M, 1≤ y ≤ N
′
in the case of the vertical block. rand
x,y
(K
i
, r
max
)
denotes a pseudo random number generator with
a derived subkey K
i
as a random seed, which gen-
erates a random number less than r
max
at the posi-
tion (x, y) of each block. Additionally, γ is a con-
figurable parameter for Gamma correction.
(2) Compute HOG feature descriptor with a small
modification of the original HOG feature descrip-
tor (Dalal and Triggs, 2005): Firstly, the gradient
magnitudes and orientations are calculated from
each BT
i
, followed by concatenating the sum of
the gradient magnitudes within each orientation
bin of the histogram. To eliminate the possibility
of maliciously manipulating the image without al-
tering HOG feature descriptor, each block is ran-
domly re-partitioned into several sub-blocks. Af-
terwards, those sub-blocks are utilized as well in
order to compute HOG feature descriptor as given
by equation (2).
F
i
=
T
i
+
NB
∑
j=1
U
i, j
2
(2)
T
i
denotes the unnormalized HOG feature from
the entire i-th block of BT
i
, whereas U
i, j
is from
the j-th sub-block randomly selected within BT
i
,
where NB is the number of sub-blocks and k·k
2
represents the L2-norm operator. Concatenating
the normalized HOG feature F
i
of every BT
i
re-
sults in the final HOG feature descriptor repre-
sented by F = {F
1
, ..., F
r+c
}.
(3) Quantize the final HOG feature descriptor into 2
l
levels, where l is the number of bits for quanti-
zation). As for the quantization process, SMQT
is employed since it can remove a small perturba-
tion of data by performing an automatic structural
breakdown of data and building a SMQT binary
tree (Nilsson et al., 2005).
(4) Permute the quantized HOG feature descriptor
at bit-level and perform the XOR operation with
pseudorandom bits. Finally, it constructs a final
image hash, TAG
IH
.
The use of IIRT is introduced to minimize a cer-
tain level of gradient distortions caused by lossy com-
pression and noise, so that it helps to obtain more ro-
bust HOG feature descriptor. The impact of IIRT on
robustness is presented by experiments in section 4.1.
Additionally, IIRT helps to increase the security prop-
erty by producing a perceptually same image but hav-
ing different random representations and image gra-
dients. To obtain more secure hash, a bit-level per-
mutation step is employed (Xie et al., 2001) since it
can prevent an attacker from estimating the relation-
ship between any bit of TAG
IH
and a specific image
block or orientation bin. As a result, it is impossible to
estimate or manipulate HOG feature descriptor from
TAG
IH
without knowing the master secret key.
3.2 Hash Verification Procedure
3.2.1 Preprocessing
As shown in Fig. 1, the received image is prepro-
cessed in the same way as image hash generation pro-
cedure described in section 3.1.1. Thus, all the blocks
of the received image are similarly represented by
I’ = { B
′
1
, ..., B
′
r+c
} = {H
′
1
, ..., H
′
r
, V
′
1
, ..., V
′
c
}.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
374

3.2.2 Subkey Derivation
The most challenging task to derive a correct subkey
at the receiver is to obtain the same salt value from
the received image. Firstly, the coarse image repre-
sentation S
′
i
is extracted from each B
′
i
according to
the steps (1)–(4) in section 3.1.2. Since S
′
i
can be
considered as a noisy version of S
i
, all the single-
bit errors on S
′
i
can be corrected by Hamming de-
coder with the parity code bits PC
i
. PC
i
can be re-
trieved by PC = dec(K
m
, TAG
pc
), where dec(·, ·) de-
notes a symmetric decryption function. As given by
K
′
i
= kd f (K
m
, CS
i
), a subkeyK
′
i
can be derived from
CS
i
which is the corrected version of S
′
i
.
3.2.3 Image Hash Generation
At the receiver, it is not necessary to perform a bit-
level permutation since HOG feature descriptor of the
original image can be recovered from the received
TAG
IH
by applying the inverse permutation. Thus,
the steps (1)–(3) in section 3.1.3 are only performed.
3.2.4 Image Hash Verification, Tamper
Detection and Localization
HOG feature descriptor of the original image is re-
trieved from the received TAG
IH
through the in-
verse permutation. A distance between the retrieved
HOG feature descriptor and the one computed in sec-
tion 3.2.3 is compared with a threshold to verify the
authenticity and integrity of the received image. If the
distance is less than the threshold, the received image
will be declared as authentic. Otherwise, it will be
considered as non-authentic, thus a tamper detection
and localization step will be processed.
To identify the tamper regions on the received im-
age, a Sum of Absolute Differences (SAD) between
two HOG feature descriptors is calculated for each
B
′
i
. The absolute differences of each orientation bin
within HOG feature descriptor of B
′
i
will be com-
pared with a threshold, then accumulated if the dif-
ference is larger than the threshold. In this manner,
any B
′
i
where has non-zero SAD value are indicated
as a candidate being manipulated. Finally, the inter-
section of all candidate blocks will be considered as
a tampered area. Fig. 2 shows a tampered image and
the result of the tamper localization on a given image.
4 EXPERIMENTAL RESULTS
The proposed method is evaluated by experiments
with respect to robustness, discriminability, and secu-
rity. In experiments, 30 images (512× 512 grayscale
(a) (b)
(c) (d)
Figure 2: Example of tamper localization. (a) Original im-
age. (b) Tampered image (Tampered region with a size of
80×80). (c) SAD map. (d) Tamper localized image.
with 8-bit per pixel) from USC-SIPI database and
their several modifications are used. As for the mod-
ifications, three types of allowable modifications –
JPEG/JPEG2000 compression (QF between 10 to 75
and Compression ratio between 1:5 to 1:100 respec-
tively) and Additive White Gaussian Noise (AWGN)
over a Rayleigh-fading channel with Binary Phase
Shift Keying modulation without using the channel
coding (BER between 10
−4
and 10
−2
) – are applied.
Besides, one image tampering operation that com-
bines a part of another image with the original image
dataset is adopted for content changing manipulation.
The algorithmic parameters of the proposed
method are chosen as, r = c = 16 resulting in a total
of 32 blocks (16 horizontal blocks of 32×512 and 16
vertical blocks of 512×32), p = 8, d = 16, q = 8, n =
15, and k = 11 for the subkey derivation process, γ =
1.6, r
max
= 640, NB = 64, l = 5, and the number of
orientation bins = 9 for the hash generation process.
4.1 Robustness
Robustness is evaluated by measuring the relative Eu-
clidean distance between HOG feature descriptors of
the original and distorted images by acceptable mod-
ifications. Fig. 3 compares the results of the proposed
method with others computed without applying IIRT
or SMQT quantization to investigate the impact of
IIRT and SMQT in the proposed method.
In the case of without applying IIRT, the distance
increases significantly and reaches a peak of around
0.11, 0.14, and 0.08 respectively for image compres-
AHybridApproachforContentBasedImageAuthentication
375
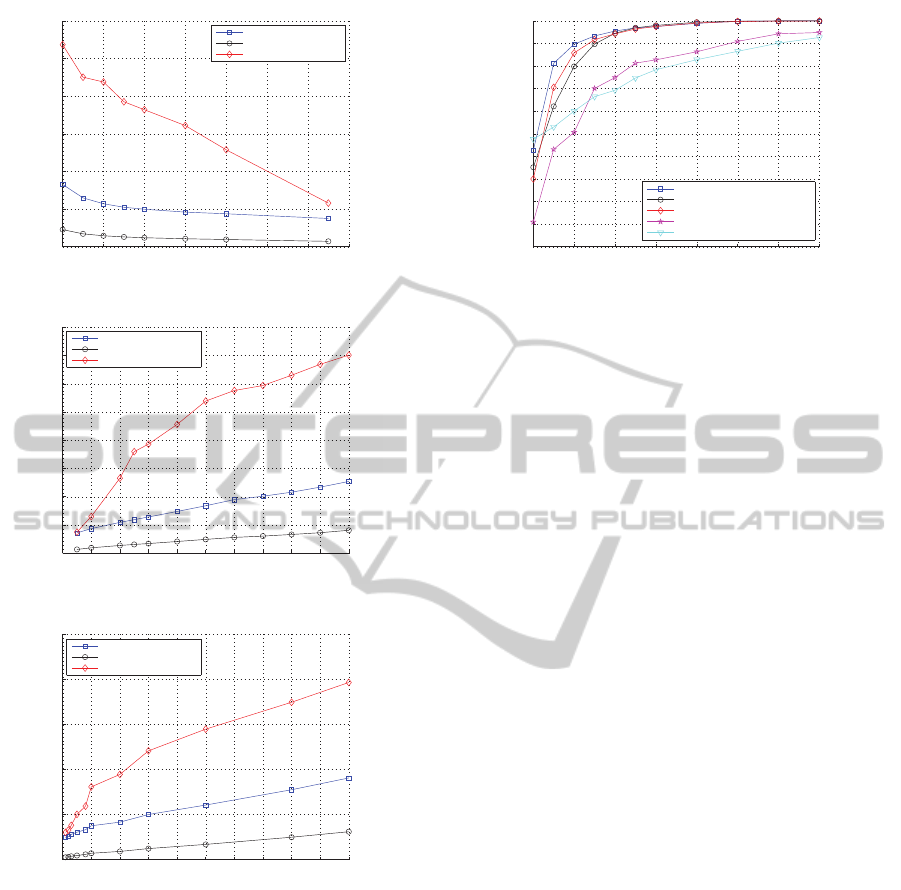
10 20 30 40 50 60 70 80
0
0.02
0.04
0.06
0.08
0.1
0.12
Quality Factor
Relative Euclidean Distance
Proposed method
Proposed method (w/o SMQT)
Proposed method (w/o IIRT)
(a) JPEG compression.
1:10 1:20 1:30 1:40 1:50 1:60 1:70 1:80 1:90 1:100
0
0.02
0.04
0.06
0.08
0.1
0.12
0.14
0.16
Compression Ratio
Relative Euclidean Distance
Proposed method
Proposed method (w/o SMQT)
Proposed method (w/o IIRT)
(b) JPEG 2000 compression.
0 0.001 0.002 0.003 0.004 0.005 0.006 0.007 0.008 0.009 0.01
0
0.02
0.04
0.06
0.08
0.1
Bit Error Ratio (BER)
Relative Euclidean Distance
Proposed method
Proposed method (w/o SMQT)
Proposed method (w/o IIRT)
(c) AWGN.
Figure 3: Relative Euclidean Distance between HOG fea-
ture descriptors of the original and modified image for
three approaches: Proposed method with IIRT (quantized
by SMQT), Proposed method with IIRT (no quantization),
and Proposed method without IIRT.
sions and AWGN as the compression and error ratio
increase. However, applying IIRT before HOG com-
putation improves the robustness by keeping the dis-
tance less than 0.02 through all the content preserving
modifications when HOG feature descriptors are not
quantized. It is also observed that the distance in the
presence of SMQT quantization errors still remains
relatively small – less than 0.04, 0.05, and 0.04 re-
spectively – even though it slightly increases the over-
all distance.
16x16 32x32 48x48 64x64 80x80 96x96 112x112 128x128
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
The size of tampered area
Area Under the ROC curve (AUC)
Proposed method (r = 16, c = 16)
Proposed method w/o KDF (r = 16, c = 16)
Proposed method (r = 8, c = 8)
Venkatesan et al.
Xie et al.
Figure 4: Discriminability comparison.
4.2 Discriminability
Discriminability is assessed by how well the proposed
method can distinguish content changing manipula-
tions from content preserving modifications. To do
this, the distances between the original and manipu-
lated images with various size of tampered region are
compared with the results of content preserving mod-
ifications by applying Receiver Operating Character-
istics (ROC) analysis. The experiments to investigate
the influences of KDF and algorithmic parameters r
and c are also conducted. More importantly, the per-
formance of the proposed method is compared with
two existing methods (Venkatesan et al., 2000; Xie
et al., 2001) since both of them demonstrated a bet-
ter discriminability than the other algorithms in (Shin
and Ruland, 2013).
As presented in Fig. 4, the proposed method
achieves excellent discriminability and even outper-
forms two existing methods. The influence of KDF
is observed that applying KDF can improve discrim-
inability especially when the size of tampered area
is relatively small. For example, KDF increases the
Area Under the ROC Curve (AUC) from 0.8 to 0.9 at
the size of 32×32 and from 0.6 to 0.8 at the size of
24×24. As for the impact of the algorithmic parame-
ters r and c which respectively represent the number
of horizontally and vertically partitioned blocks, the
results indicate that the larger r and c, the better per-
formance can be achieved. However, there is a trade-
off between the performanceand the final hash length.
4.3 Security
To evaluate the security of the proposed method, this
paper employs two desirable properties presented in
(Coskun and Memon, 2006): (a) Confusion - The
complexity of the relation between the key and the
hash value, (b) Diffusion - The irrelevance between
the perceptual information of the input and the hash
SECRYPT2014-InternationalConferenceonSecurityandCryptography
376
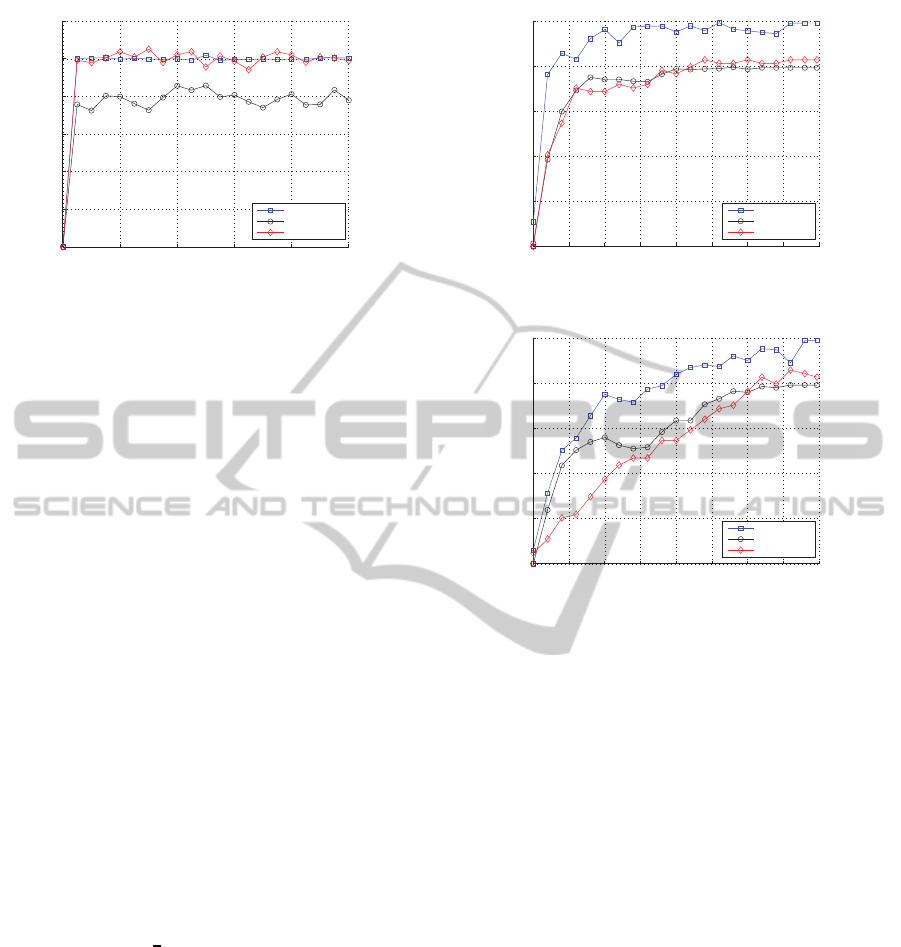
0 200 400 600 800 1000
0
0.1
0.2
0.3
0.4
0.5
0.6
Difference from the initial master secret key value
Normalized Hamming Distance
Proposed method
Venkatesan et al.
Xie et al.
Figure 5: Normalized Hamming Distance of hash values
under 1000 different master secret keys.
value. Thus, it is desirable that a small perceptual
change on the image content or a single bit change
of the secret key can cause a significant change on
the output hash value. The experiments conducted in
(Coskun and Memon, 2006) are reproduced.
Concerning the experiments for the confusion ca-
pability, an initial master key is randomly selected and
sequentially increased by one to generate 1000 dif-
ferent master keys. Afterwards, the final hash value
calculated using the initial master key is compared
with the ones obtained from other keys to verify the
statistical irrelevance between them by measuring the
normalized Hamming distance. Fig. 5 shows that the
mean distance of all three methods stays around 0.50,
0.40, and 0.51 respectively, which indicates that they
possess good confusion capability.
The diffusion capability is evaluated by measur-
ing the normalized Hamming distance as the percep-
tual units of an image are gradually replaced with the
corresponding units of another image in two different
ways, either by random substitution or local substitu-
tion. The random substitution is to randomly select
the perceptual units and replace them whereas the lo-
cal substitution is to select a specific perceptual unit
and grow the regions. Note that 16×16 blocks over-
lapped with ratio of
1
2
in both horizontal and vertical
direction is considered as the perceptual unit in the
experiments.
As shown in Fig. 6, changing a single perceptual
unit cannot result in a completely different hash value
regardless of the substitution scheme due to the ro-
bustness property of the hash algorithm. In the case
of the random substitution, however, the normalized
Hamming distance of the proposed method signifi-
cantly increases until reaching around 0.4 where 250
out of 3969 perceptual units are randomly substituted,
and then slowly increases up to almost 0.5. On the
other hand, the replacement of more than 1750 per-
ceptual units is required for two existing methods in
0 500 1000 1500 2000 2500 3000 3500 4000
0
0.1
0.2
0.3
0.4
0.5
Number of different pereptual units
Normalized Hamming Distance
Proposed method
Venkatesan et al.
Xie et al.
(a) Random substitution.
0 500 1000 1500 2000 2500 3000 3500 4000
0
0.1
0.2
0.3
0.4
0.5
Number of different pereptual units
Normalized Hamming Distance
Proposed method
Venkatesan et al.
Xie et al.
(b) Local substitution.
Figure 6: Normalized Hamming Distance of hash values
under two types of substitution.
order to reach the distance of 0.4. Compared to the
random substitution, all three methods achieve much
worse diffusion capability when applying the local
substitution. Since most of the existing image hash-
ing algorithms are designed to divide an image into
several blocks and construct a hash value using robust
features extracted from each block, it is obvious that
the localized distortion produces a more similar hash
value than the randomly distributed distortion. How-
ever, the experimental results show that the proposed
method still outperforms the other methods.
5 CONCLUSIONS
In this paper, a hybrid approach combining HOG fea-
ture descriptor with the subkey derivation using the
modified DCT-SVD hashing algorithm is proposed
and evaluated in terms of robustness, discriminability,
and security. HOG feature descriptor computed from
the randomly transformed image by IIRT is used as
the invariant features to achieve the robustness. On
the other hand, the coarse image representation ob-
AHybridApproachforContentBasedImageAuthentication
377

tained by the modified DCT-SVD hashing algorithm
is considered as a salt value in KDF to derive a stable
subkey in conjunction with ECC for each horizontal
and vertical image block. The derived subkey is uti-
lized as a random seed for each corresponding block
during HOG feature computation. In such a way, the
proposed method can improve the discriminability by
producing a different subkey that will generate a to-
tally different HOG feature descriptor for the manip-
ulated block. Additionally, the security property of
the proposed method mainly relies on the randomness
introduced by IIRT, random re-partitioning, and bit-
level permutation. The use of KDF also helps to pro-
vide better security by deriving a subkey from the im-
age content and utilizing it as a secret key for each im-
age instead of reusing the same master secret key for
all the images. Thus, it can prevent an attacker from
estimating the secret key based on the large number
of image and corresponding hash value pairs.
Based on the experimental results, it is observed
that the proposed method can successfully distin-
guish the malicious manipulations from the content
preserving modifications while still having good
robustness against a certain level of distortions
caused by acceptable modifications. By comparing
with two representative methods in the literature, this
paper presents that the proposed method outperforms
them with respect to discriminability and security.
More importantly, an excellent tamper localization
capability is demonstrated as well.
ACKNOWLEDGEMENTS
This work was funded by the German Research Foun-
dation (DFG) as part of the research training group
GRK 1564 ‘Image New Modalities’.
REFERENCES
Boncelet, C. (2006). The ntmac for authentication of noisy
messages. IEEE Trans. Inf. Forensics and Secur.,
1(1):35–42.
Coskun, B. and Memon, N. (2006). Confusion/diffusion
capabilities of some robust hash functions. In Proc.
Conf. Inf. Sci. and Syst., pages 1188–1193.
Dalal, N. and Triggs, B. (2005). Histograms of oriented
gradients for human detection. In Proc. IEEE Com-
put. Soc. Conf. on Comput. Vis. and Pattern Recognit.,
volume 1, pages 886–893.
Graveman, R. and Fu, K. (1999). Approximate message au-
thentication codes. In Proc. 3rd Annual Fedlab Symp.
on Adv. Telecommun./Inf. Distrib.
Han, S.-H. and Chu, C.-H. (2010). Content-based image
authentication: current status, issues, and challenges.
Int. J. of Inf. Secur., 9(1):19–32.
Haouzia, A. and Noumeir, R. (2008). Methods for image
authentication: a survey. Multimed. Tools and Appl.,
39(1):1–46.
Hsu, C.-Y., Lu, C.-S., and Pei, S.-C. (2009). Secure and
robust sift. In Proc. ACM Int. Conf. on Multimed.,
pages 637–640.
ISO/IEC9797 (2011). Information technology – security
techniques – message authentication codes (macs).
Kozat, S., Venkatesan, R., and Mihcak, M. (2004). Ro-
bust perceptual image hashing via matrix invariants.
In Proc. IEEE Int. Conf. on Image Process., volume 5,
pages 3443–3446.
Krawczyk, H. and Eronen, P. (2010). Hmac-based extract-
and-expand key derivation function (hkdf). RFC 5869.
Lin, C.-Y. and Chang, S.-F. (2001). A robust image authen-
tication method distinguishing jpeg compression from
malicious manipulation. IEEE Trans. Cir. and Sys. for
Video Technol., 11(2):153–168.
Mihcak, M. K. and Venkatesan, R. (2001). New iterative ge-
ometric methods for robust perceptual image hashing.
In Revised Papers from the ACM CCS-8 Workshop on
Secur. and Priv. in DRM 01, pages 13–21.
Monga, V. and Evans, B. (2006). Perceptual image hashing
via feature points: Performance evaluation and trade-
offs. IEEE Trans. on Image Process., 15(11):3452–
3465.
Nilsson, M., Dahl, M., and Claesson, I. (2005). The succes-
sive mean quantization transform. In Proc. IEEE Int.
Conf. on Acoust., Speech, and Signal Process., vol-
ume 4, pages 429–432.
NIST-FIPS (2013). Digitalsignature standard (dss). Federal
Information Processing Standards Publication (FIPS
PUB) 186-4.
NIST-SP (2009). Recommendation for key derivation using
pseudorandom functions. Special Publication 800-
108.
Queluz, M. (1998). Towards robust, content based tech-
niques for image authentication. In Proc. IEEE Int.
Workshop on Multimed. Signal Process.
Shin, J. and Ruland, C. (2013). A survey of image hashing
technique for data authentication in wmsns. In Proc.
IEEE Int. Conf. on Wirel. and Mob. Comput., Netw.
and Commun., pages 253–258.
Ur-Rehman, O. and Zivic, N. (2013). Fuzzy authentication
algorithm with applications to error localization and
correction of images. WSEAS Trans. on Syst., 12:371–
383.
Venkatesan, R., Koon, S.-M., Jakubowski, M. H., and
Moulin, P. (2000). Robust image hashing. In Proc.
IEEE Int. Conf. on Image Process., volume 3, pages
664–666.
Xie, L., Arce, G., and Graveman, R. (2001). Approximate
image message authentication codes. IEEE Trans. on
Multimed., 3(2):242–252.
SECRYPT2014-InternationalConferenceonSecurityandCryptography
378
