Applications of Genetic Algorithm on Optimal Sequence

for Parrondo Games

Degang Wu and Kwok Yip Szeto

Department of Physics, The Hong Kong University of Science and Technology, Clear Water Bay, Hong Kong, Hong Kong

Keywords:

Genetic Algorithm, Parrondo Game, Optimization, Game Theory.

Abstract:

Parrondo game, which introduction is inspired by the ﬂashing Brownian ratchet, presents an apparently para-

doxical situation where there are ways to combine two losing games into a winning one. The original Parrondo

game consists of two individual games, game A and game B. Game A is a slightly losing coin-tossing game.

Game B has two coins, with an integer parameter M. If the current cumulative capital (in discrete unit) is a

multiple of M, an unfavorable coin p

is used, otherwise a favorable p

coin is used. Game B is also a losing

game if played alone. Paradoxically, combination of game A and game B could lead to a winning game,

either through random mixture, or deterministic switching. In deterministic switching, one plays according

to a sequence such as ABABB. Exhaustive search and backward induction have been applied to the search

for optimal ﬁnite game sequence. In this paper, we apply genetic algorithm (GA) to search for optimal game

sequences with a given length N for large N. Based on results obtained through a problem-independent GA,

we adapt the point mutation operator and one-point crossover operator to exploit the structure of the optimal

game sequences. We show by numerical results the adapted problem-dependent GA has great improvement in

performance.

1 INTRODUCTION

Inspired by the ﬂashing ratchet, Parrondo invented the

games of chance later known as Parrondo game (Par-

rondo, 1996), in which two losing games can be com-

bined following a random or periodic strategy leading

to a winning game. Later, (Allison and Abbott, 2002)

and (Toral et al., 2003) demonstrated that Parrondo

game can be described by a discrete Fokker-Planck

equation, thus a more rigorous relation between Par-

rondo game and Brownian ratchet was established.

From the perspective of game, the optimal sequence

for a given set of parameters for Parrondo games was

inferred by Dinis using dynamic programming (Di-

nis, 2008). It is worth noting that greedy algorithms

do not work in ﬁnding the optimal game sequence for

a ﬁnite length.

Multi-player versions of the games have been pro-

posed, and they exhibit counterintuitive phenomena

resembling those observed in game, control, and op-

timization theories or economics. Many researchers

have found that greedy algorithms or strategies may

lead to suboptimal or even losing solutions in these

models (Dinis and Parrondo, 2003; Dins and Par-

rondo, 2004; Parrondo et al., 2007). Optimiza-

tion problems of this type warrant the use of meta-

heuristic algorithm such as genetic algorithms (Gold-

berg and Holland, 1988; Holland, 1975).

The successful application of genetic algorithm

has been demonstrated in the solution of many en-

gineering problems, such as speed control of brush-

less DC motor (Xia et al., 2004), cyclic-steam oil

production optimization problem (Patel et al., 2005),

traveling salesman problem (Jiang et al., 2000), mo-

bile robot motion control (Messom, 2002), model-

ing adaptive agents in stock markets (Fong and Szeto,

2001; Szeto and Fong, 2000), and the problem of air-

port scheduling (Shiu and Szeto, 2008). In science,

genetic algorithm has also been used with good re-

sults in ﬁelds such as biology (Clote, 2005; Ding and

Zhang, 2008; Pond et al., 2006), clusters (Doye, 2002;

Wales et al., 2000; Wales et al., 1998) and glass tran-

sition (Debenedetti and Stillinger, 2001) in condensed

matter physics.

Our objective of this paper is to use genetic algo-

rithm on the search for optimal game sequence of long

length. We ﬁrst use Dinis algorithm to gain insight

of the structure of optimal sequences with moderate

length. We then propose structure-preserving evo-

lution operators (mutation and one-point crossover

Wu D. and Szeto K..

Applications of Genetic Algorithm on Optimal Sequence for Parrondo Games.

DOI: 10.5220/0005070400300037

In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 30-37

ISBN: 978-989-758-052-9

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

operators), coupled with an appropriate structure-

preserving population initialization procedure to ﬁnd

the optimal sequence for longer game sequence. Here

structure-preserving condition means that the search

process impose certain constraints on the patterns that

are observed in the optimal sequences of moderate

length, as found either by exhaustive search or Di-

nis algorithm. In order to assess the effect of the

constraints on the quality of the solution, we ﬁrst

use simple genetic algorithm as a biased sampling

method in order to justify the adaptive approach we

use later. Our paper is organized as follows. In Sec-

tion 2, we introduce the Parrondo game and discuss

the Dinis algorithm that reveals some speciﬁc patterns

which appear in the optimal sequence of moderate

length. In Section 3, we propose structure-preserving

mutation and one-point crossover and corresponding

structure-preserving population initialization proce-

dure. In Sections 4 and 5, we discuss the experiment

design and present the experiment results. Finally, the

concluding remarks can be found in Section 6.

2 PARRONDO GAMES

The original Parrondo game consists of two individ-

ual coin tossing games, namely game A and game B.

Game A has only one coin, whose winning probabil-

ity is p

= 1/2 − ε, where ε is a small and positive

number. Let X(t) be the cumulative capital of the

player at time t, an integer. If the player keeps playing

game A, the average capital satisﬁes

hX(t + 1)i = hX(t)i + 2p

+ 1 (1)

where h·i is understood as ensemble average. Game

B has two coins, one “good” coin and one “bad” coin.

Game B has an integer parameter M. If X(t) is a

multiple of M, then X(t + 1) is determined by the

“bad” coin with winning probability p

= 1/10 − ε,

otherwise the “good” coin with winning probability

= 3/4 − ε is used. Similar to game A, if the player

keeps playing game B only, the average capital satis-

ﬁes

hX(t + 1)i = hX(t)i + 2[π

(t)p

+ (1 − π

(t))p

] − 1

(2)

which explicitly depends on π

(t), the probability that

the capital X(t) = 0 mod M. (Harmer and Abbott,

1999) showed that game B is a losing game when

= 1/10 −ε, p

= 3/4 −ε and M = 3, with positive

ε. In this paper, we only discuss the case when M = 3.

There is a recent article discussing the phase diagram

of the more complex situation where the games are

two B games with different M (Wu and Szeto, 2014).

Such extended Parrondo game with multiple M ex-

hibits interesting phenomena such as weak and strong

Parrondo effects when the sequence is inﬁnite.

If we model the Parrondo game as a discrete-

time Markov chain as in (Harmer and Abbott,

2002), we can deﬁne the probability vector π

π(t) ≡

(π

(t), π

(t))

(for M = 3). Accordingly, the

transition matrix for game A is





0 1 − p

1 − p





(3)

such that the time evolution equation is π

π(t + 1) =

π(t). Similarly, the transition matrix for game B is





0 1 − p

1 − p





(4)

Parrondo game can be played according to a deter-

ministic ﬁnite game sequence such as ABABB, so at

the end of the sequence, the probability vector π

π(5) is

π(5) = Π

π(0). (5)

Algorithm 1: Function to calculate the expected return

for game sequence {S

} with length N.

function EXPECTED RETURN({S

})

g ← 0

π = [1,0,0]

for t ← 1,N do

if S

= A then

g ← g + π

[2p

− 1,2p

− 1]

π ← Π

else

g ← g + π

[2p

− 1,2p

− 1]

π ← Π

end if

end for

return g

end function

Parrondo game has a seemingly paradoxical prop-

erty that while game A and B are losing when they are

played individually, the stochastic mixture of game

A and B, or playing according to a deterministic se-

quence may lead to a winning combined game for

small positive value of ε. For the detailed analysis

of this paradox, please refer to (Harmer and Abbott,

2002). For a ﬁnite game sequence with length N,

the expected return at the end of the game sequence

can be computed by Algorithm 1. Our task is to ﬁnd

the ﬁnite game sequence that has maximum cumula-

tive gain. The expected return per game in the sta-

tionary state for a periodic sequence with length N

ApplicationsofGeneticAlgorithmonOptimalSequenceforParrondoGames

can be computed using Algorithm 1 with two mi-

nor modiﬁcations: the initial value of π

π should be

the equilibrium distribution of the transition matrix

α(1)

α(2)

·· ·Π

α(N)

and the ﬁnal value of g should

be divided by N.

Sequences up to period 12 have been studied

using symbolic manipulators and exhaustive search

(Wagon and Velleman, 2001), and the periodic se-

quence ABABB, or any of its permutations, has come

up as the best in the sense that it provides the high-

est returns in the stationary state. However, exhaus-

tive search for optimal sequences of ﬁnite length N

is not feasible for large N. Using dynamic program-

ming, Dinis discovered that optimal sequences with

ﬁnite N “consist of several repetitions of the ABABB

motif ﬂanked by brief pieces of other sequences. (Di-

nis, 2008) For example, the optimal sequence for

N = 20 with initial condition X (t) = 0 and ε = 0 is

AB ABABBABABBABABB ABB. In fact, the struc-

ture of the optimal sequences is more speciﬁc: they

are strings of AB and ABB. From these results, we

have the following deﬁnition:

Deﬁnition 1. A game sequences is said to have a spe-

cial structural-property if it is made of AB and/or ABB

substrings exclusively.

Straightforward implementation of Dinis algo-

rithm requires storage space that scales as N, in or-

der to store all the numerical results from all inter-

mediate steps. Moreover, the algorithm approximates

two-dimensional plane with a discrete square grid (In

(Dinis, 2008), a 2000 × 2000 grid was used for each

step). The error in the expected payoff due to grid ap-

proximation will accumulate across time and the total

error in the expected payoff at the end of the sequence

is at least a linear function of N. The effect of this

error to the correctness of the optimal sequence has

not been investigated. The approximation therefore

constraints the computation of optimal sequences for

large N. This suggests that heuristic algorithms such

as GA that demands much less space and does not re-

quire approximation in the expected payoff are useful

for optimal sequences with long length. Moreover,

by deﬁnition, Dinis’ algorithm does not provide any

information of the suboptimal sequence. In contrast,

while searching for the optimal solution, GA also ef-

ﬁciently samples many suboptimal solutions, which

provide insights in the relation between the structure

of a sequence and its performance.

3 STRUCTURE-PRESERVING

GENETIC ALGORITHM

3.1 Representation

If we map game A to 0 and map game B to 1, a game

sequence with length N can be mapped to a binary

string with the same length, and the order of the bi-

nary values corresponds to the order the games are

played. The objective function is given by Algorithm

1. For example, the game sequence ABABB is en-

coded as 01011. For game sequences that are strings

of AB and ABB, an auxiliary representation is use-

ful: 0 for AB and 1 for ABB. For example, game

sequence ABABB is encoded as 01 in this auxiliary

representation. However, game sequences under this

auxiliary representation vary in length from sequence

to sequence. To distinguish these two kinds of repre-

sentations, we call the one that maps game A to 0 the

original representation.

3.2 Simple Genetic Algorithm

A simple genetic algorithm is used as the reference.

Algorithm 2: “Simple” Genetic Algorithm.

procedure SGA

INIT(P)  P for the population

repeat

← DET TOURNAMENT(P,k)

for i = 0,SIZE(P)/2-1 do

if RAND()< p

then

XOVER(P

(2i),P

(2i + 1))

end if

end for

for i = 0,SIZE(P)-1 do

for j = 0, N − 1 do

if RAND()< p

then

FLIP(P

(i, j))

end if

end for

P ← P

EVALUATE(P)  update the ﬁtness values

until Stopping criteria satisﬁed

end procedure

In the initialization, each locus of each chromo-

some is set to 1 or 0 with equal probability. The new

population P

is generated from the last one using

deterministic tournament: from previous generation,

randomly draw k chromosomes with equal probabil-

ity, and select the one with the highest ﬁtness value.

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

This process is repeated until the new population has

the same number of chromosomes as the previous

population. The one-point crossover operator is de-

noted by XOVER(), and its rate is denoted by p

. The

mutation rate per bit is denoted by p

3.3 Structure-preserving Mutation

Operator

If a chromosome has special structural property, we

can apply a mutation operator that preserves this prop-

erty. We propose a structure-preserving mutation op-

erator in Algorithm 3.

Algorithm 3: Structure-preserving Mutation Operator.

function SPMUTATE(c)  c for a chromosome

← ORIGINTOAUX(c)

for j = 0,SIZE(c

)−1 do

if RAND()< p

then

FLIP(c

( j))  c

( j) is the j-th locus of c

c ←AUXTOORIGINAL(c

)

end if

end for

return c

end function

However, when we use Algorithm 3, we must

check if the sequence after mutation has length N.

We therefore need an algorithm for chromosome re-

pair, using ﬁrst a conversion function AUXTOORIG-

INAL(c

). This function converts c

in the auxiliary

representation back to a chromosome in the original

representation, which is not always possible because

the converted chromosome in original form may have

a length greater or less than N. If SIZE(c)> N, we then

pop 01 or 011 from the back of c until SIZE(c)< N.

We append 01 or 011 to the back of c such that

SIZE(c)= N.

3.4 Structure-preserving Crossover

Operator

If a chromosome has special structural property, we

can apply an adapted one-point crossover operator

that preserves this propose. The structure-preserving

one-point crossover operator is shown in Algorithm 4.

Here the function CHOOSEXPT decides the

crossover point in the auxiliary representation such

that the two children chromosomes in the original rep-

resentation are either one bit longer or shorter than N.

The function FIXCHROMOSOME lengthens or short-

ens the chromosome by mutating 01 to 011, 011 to 01,

converting 011 to 0101, or converting 0101 to 011.

Algorithm 4: Structure-preserving One-point cross-

over operator.

procedure SPXOVER(c

)

← AUXREPRE(c

)

← AUXREPRE(c

)

xPt ← CHOOSEXPT(c

)

XOVER(c

,xPt)

← FIXCHROMOSOME(c

)

← FIXCHROMOSOME(c

)

← AUXTOORIGINAL(c

)

← AUXTOORIGINAL(c

)

end procedure

3.5 Structure-preserving Genetic

Algorithm

In order to replace the mutation operator and one-

point crossover operator with the structure-preserving

versions, the chromosomes must have special struc-

tural property at all time. For this purpose, a structure-

preserving initialization routine is propose in Algo-

rithm 5.

As we will show later, this initialization routine

per se greatly improves the quality of the initial chro-

mosomes. In this paper, the structure-preserving ge-

netic algorithm (SPGA) refers to ones that run in the

framework of Algorithm 2, with population initial-

ized by Algorithm 5, the mutation operator replaced

by Algorithm 3 and the one-point crossover opera-

tor replaced by Algorithm 4. This combination of

algorithms in SPGA reduces the search space sub-

stantially. One concern about this reduction is that

it might fragment the solution space into disjoint sub-

space. We will discuss this issue in Section 5.

Algorithm 5: Structure-Preserving Initialization.

procedure SPINIT(P)

for each c

in P do

empty c

append 01 or 011 randomly to c until

SIZE(c)==N

end for

end procedure

4 EXPERIMENTAL DESIGN

For comparison of the relative efﬁciency of the vari-

ous components of our genetic algorithm, we consider

the following versions of GAs.

ApplicationsofGeneticAlgorithmonOptimalSequenceforParrondoGames

• SGANoX: A GA that uses only the mutation oper-

ator, with uniform initialization and no crossover

operators

• SGANoXwSPInit: SGANoX with structure-

preserving initialization

• SGA: Simple Genetic Algorithm, with uniform

initialization, standard mutation operator and one-

point crossover operator

• SGAwSPInit: Simple Genetic Algorithm with

structure-preserving initialization, standard muta-

tion operator and one-point crossover operator

• SPGANoX: Structure-preserving mutation only

genetic algorithm with structure-preserving ini-

tialization and structure-preserving mutation op-

erator, but without crossover

• SPGA: Structure-preserving genetic algorithm

with structure-preserving initialization, structure-

preserving mutation operator and structure-

preserving crossover operator

For simplicity, when we use the term SGAs, we

mean the group of SGA, including SGANoX, SGA,

SGANoXwSPInit, SGAwSPInit. Similarly, when we

use the term SPGAs, we mean the group of SPGA,

including SPGANoX, SPGA.

The size of the population, N

, will be set to

100 for all versions of GAs. The size of the tourna-

ment, k, deﬁned in Algorithm 2 in the deterministic

tournament selection process will be set to 10. The

crossover rate, p

and the mutation rate per bit, p

both deﬁned in Algorithm 2, will be chosen individu-

ally for each GA such that each GA has good perfor-

mance.

5 RESULTS AND ANALYSIS

First we investigate the effect of imposing structure-

preserving evolution operators and population initial-

ization on search space. Exhaustive search is not an

option for sequences, as long as N = 80. Instead

we use SGA to perform a biased sampling on the

search space by just running SGA with p

= 0.02 and

= 1.0. The selection mechanism in SGA biases

towards chromosomes having higher ﬁtness values.

Every chromosome that appears during 200 genera-

tions of evolution from 50 independent experiments

are collected as samples. Numerical results show that

the ﬁtness distribution for game sequences satisfy-

ing special structural property are strongly grouped

together at high ﬁtness values, and they are among

the chromosomes having ﬁtness values mostly higher

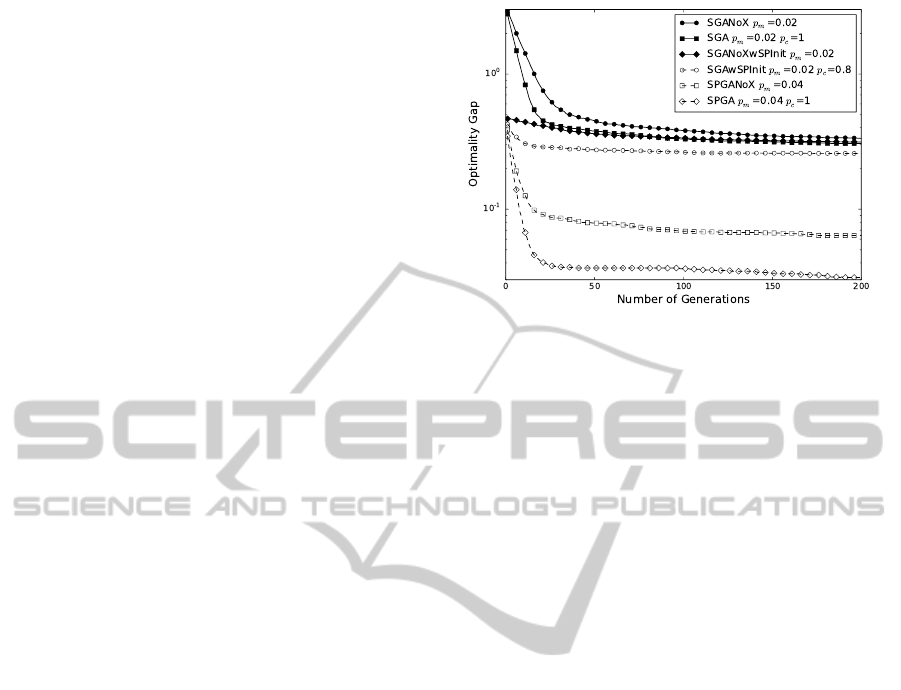
Figure 1: Optimality gap as a function of number of gen-

erations for N = 80. Every curve is an average from 100

independent experiments. Y-axis is in log-scale. The gap is

smallest for SPGA, indicating it is the best performing GA.

than the highest ﬁtness of the sequences without spe-

cial structure. From this observation, we conclude

that imposing structure-preserving evolution opera-

tors and population initialization on search space will

not fragment the search space. Furthermore, the usage

of structure-preserving evolution operators and popu-

lation initialization can be justiﬁed due to the overall

higher ﬁtness value obtained.

Next we compare the performances of the various

GAs mentioned in the last section on the search for

optimal sequence of with N = 80. We ﬁrst calculate

the true expected return of the optimal sequence using

Dinis’ algorithm. We then measure the performance

of various GAs by the optimality gap, the difference

between the expected return of the optimal sequence

and the expected return of the chromosome with the

highest ﬁtness value. We show the optimality gap as

a function of number of generations in Fig. 1. The

values of p

and p

are chosen on the basis of perfor-

mance.

The structure-preserving initialization alone con-

tributes signiﬁcantly to the performance, as can be

seen from the relative performances of SGANoX

and SGA with or without structure-preserving pop-

ulation initialization in Fig. 1. In the case

of problem-independent GAs, one-point crossover

operator contributes to the early edge in perfor-

mance. The problem-dependent structure-preserving

GAs generally perform better. SPGANoX outper-

forms SGAwSPInit. SPGA performs the best.

Since there is no guarantee that optimal game se-

quence will be obtained after 200 generations, we

therefore need to assess the average quality of the best

solutions after 200 generations. For N=80, the opti-

mal game sequence is

ABXXXXXXXXXXXXXXXABB, (6)

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

where X stands for ABABB. We call those AB (or

ABB) substring that are not able to form ABABB with

adjacent substring ungrouped AB (or ABB).

A typical suboptimal but still good solution re-

sulted from SPGAs has the following structure:

XXXXXXABBXXXXABBXXXABXAB, (7)

which possesses the right number of AB and ABB

substrings, and the SPGAs manage to ﬁgure out the

overall structure. From this observation, we expect

that a problem-speciﬁc local search can obtain the real

optimal solution from the best solution obtained from

SPGAs. In this context, we may introduce some alter-

native quality measures by the following enquiries:

1. Has the right number of AB and ABB been reached?

(Here the right number refers to the number in the opti-

mal sequence.) If not, calculate the deviation by

(s) = |N

(s) −N

∗

)| + |N

ABB

(s) − N

ABB

∗

)|,

(8)

where N

(s) (N

ABB

(s)) is the number of AB (ABB re-

spectively) and s

∗

is the optimal sequence.

2. If the right number of AB and ABB has been reached,

has the right number of ungrouped AB and ABB been

reached? (Here, the right number again refers to the

number in the optimal sequence.) If N

∗

(s) (N

∗

ABB

(s))

is the number of ungrouped AB (ABB respectively) and

∗

is the optimal sequence, then this deviation can be

written as

(s) = |N

∗

) − N

∗

(s)| + |N

∗

ABB

∗

) − N

∗

ABB

(s)|.

(9)

For both measures, the smaller the values of d

(s)

and d

(s) the higher is the quality of the sequence. We

show the statistics of the best chromosomes obtained

by various GAs at the end of 200-th generation in Ta-

ble 1. Data are collected from 100 independent exper-

iments for each GA variant. As can be seen from the

table, SPGAs are better at ﬁguring out the structure of

the optimal sequence than other GAs.

We see that for medium size sequence (N = 80),

our SPGA is good approximation to Dinis analysis, as

shown in Fig. 1. Thus for medium size sequence, we

do not see the advantage of our SPGA algorithm.

We now apply the same set of GAs on searching

for the optimal sequences with longer length N. The

values of p

and p

are the same as those used be-

fore. Note that the exact optimal sequence with length

N = 200 is not easily available as straightforward im-

plementation of Dinis algorithm needs huge amount

of storage space and exhaustive search will require

even more. Thus, we use an alternative measure of

performance: we record the highest ﬁtness value in

the population as a function of the number of gen-

erations, averaged over 50 independent experiments

and see which GA yields the best result. The perfor-

mances of various GAs as a function of number of

Table 1: Statistics of the best chromosomes obtained by

various GAs at the end of 200-th generation for N = 80.

Data are collected from 100 independent experiments for

each GA variant. The best chromosomes obtained from

SGAs do not necessarily satisfy the special structural prop-

erty, and therefore the numbers of instances of best chro-

mosomes that satisfy the property are indicated. The quan-

tity Prs stands for the Probability that Structural property is

observed over 100 independent experiments. In the calcu-

lation of the quality measure, d

(s) and d

(s) for the case

of SGA, we only count those chromosomes satisfying the

special structural property.

GA Variant Prs d

(s) d

(s)

SGANoX 97/100 3.60825 7.87629

SGA 96/100 3.48958 6.84375

SGANoXwSPInit 97/100 4.89691 8.17526

SGAwSPInit 100/100 4.75 6.47

SPGANoX 100/100 0.25 0.89

SPGA 100/100 0.00 0.54

generation when searching for optimal sequence with

length N = 200 are shown in Fig. 2. We see that SP-

GAs outperform problem-independent SGAs. In fact,

for SGAs with structure-preserving initialization, the

average best ﬁtness value drops as the number of gen-

eration increases. Let us compare this curious fea-

ture of decreasing average ﬁtness of SGAs for large

N(= 200) with the results for small N(= 80) shown

in Fig. 1. The optimality gaps are all decreasing with

generation number in Fig. 1, implying that the aver-

age ﬁtness of all GAs are increasing. We also see that

SGAs are able to take advantage of the good qual-

ity initial chromosomes resulted from the structural-

preserving initialization. However, when N is large,

as shown in Fig. 2 for N = 200, SGAs no longer have

the ability in exploiting the good quality of the initial

chromosomes. In Fig. 2, we observe the merging of

several curves at large generation number:

1. SPGA(♦) merges with SPGANoX()

2. SGAwSPInit (◦) merges with SGA()

3. SGANoX(•) merges with SGANoXwSPInit();

We see from 1 that SPGA with crossover operator,

does not have noticeable advantage over SPGANoX

in terms of best ﬁtness value in the population, sug-

gesting structure-preserving crossover operator does

not provide additional advantage for large-size prob-

lem. From 2 we see that for SGA, the special initial-

ization with structure preserving features is irrelevant

for large N. From 3, we see similar effect as 2 without

crossover for SGA, when N is large.

In Table 2, we see the average of the best ﬁt-

ness values at the end of 200-th generation and the

standard deviation. Not only do SPGAs (SPGANoX

and SPGA) achieve higher best ﬁtness value, they

ApplicationsofGeneticAlgorithmonOptimalSequenceforParrondoGames

Table 2: Best ﬁtness values statistics for N = 200 at the end

of the experiment. Data are collected from 50 experiments.

GA Variant Avg. best ﬁtness Stand. deviat.

SGANoX 12.1 0.231

SGA 13.4 0.250

SGANoXwSPInit 12.1 0.228

SGAwSPInit 13.3 0.273

SPGANoX 15.01 0.0805

SPGA 15.00 0.0978

Table 3: Best ﬁtness values statistics for N = 300 at the end

of the experiment. Data are collected from 50 experiments.

GA Variant Avg. best ﬁtness Stand. deviat.

SGANoX 15.9 0.364

SGA 18.0 0.360

SGANoXwSPInit 15.9 0.348

SGAwSPInit 17.7 0.334

SPGANoX 21.90 0.0907

SPGA 21.97 0.0893

also have smaller standard deviation in the best ﬁt-

ness value, which means that SPGAs are more re-

liable. Moreover, SPGANoX and SPGA have sim-

ilar performance statistically, suggesting structure-

preserving crossover operator does not provide no-

ticeable additional advantage for large-size problem.

Results for optimal sequence search with length

N = 300 exhibit similar qualitative features (Table

3). SPGAs outperform SGAs in terms of aver-

age best ﬁtness value. SGAs are not able to ex-

ploit the good quality chromosomes resulted from the

structure-preserving initialization. Similar to the case

of N = 200, the structure-preserving crossover op-

erator does not provide additional beneﬁt in perfor-

mance.

Figure 2: Average best ﬁtness as a function of number of

generations for N = 200. Every curve is an average from 50

independent experiments.

6 CONCLUSIONS AND FUTURE

WORK

In this paper, we have proposed problem-dependent

structure-preserving mutation operator, one-point

crossover operator and initialization routine. We have

designed several numerical experiments to evaluate

the relative efﬁciency of several GAs incorporating

various features deemed important from observation

of small N optimal sequences. We have shown that

the proposed structure-preserving initialization rou-

tine offers high-quality candidate solutions. We have

also shown that both structure-preserving mutation

operator and one-point crossover operator improves

the performance greatly compared to various versions

of simple GAs. The various versions of SPGAs are

consistently better at ﬁguring out the structure of opti-

mal sequence for medium-size problem, e.g. N = 80.

In medium-size problems, e.g. N = 80, structure-

preserving crossover operator provides noticeable ad-

ditional advantage; however, for large-size problems,

e.g. N = 200, structure-preserving crossover oper-

ator does not provide noticeable additional advan-

tage. This observation could be useful in using GAs

to discover the structures of sequences for different

lengths. In general, our analysis using GA for Par-

rondo game sequences can be extended to the analysis

of sequences from other ﬁelds. For the future works,

we could develop a permutation-based evolution op-

erator to further improve the performance of SPGAs.

Within the conﬁne of limited numerical analysis

for long sequence, we can conclude that our algorithm

is useful in searching for the optimal sequence for Par-

rondo game. Since the exact solution is not known

for long sequence, our method does provide useful

candidates for benchmarking. This is important for

applications in other sequence analysis for which a

good solution, not the mathematically optimal one,

is needed. In the context of Parrondo game, Dinis

algorithm for short and medium sequences can pro-

vide a benchmark for the optimal solution, which we

can also obtain by SPGA. However, for very long se-

quence, when Dinis algorithm is not easily used, our

SPGA does provide a good solution. In practical ap-

plications in other sequences, we can ﬁrst analyze the

motif in short sequences where exhaustive search pro-

vide the optimal solution, and then use those motifs to

obtain a good solution for long sequence with SPGA.

ACKNOWLEDGEMENTS

K. Y. Szeto acknowledges the support of grant FS

GRF13SC25and FS GRF14SC28. Degang Wu would

ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications

like to thank Zhangyu Chang for helpful discussions.

REFERENCES

Allison, A. and Abbott, D. (2002). The physical basis

for parrondo’s games. Fluctuation and Noise Letters,

2(04):L327L341.

Clote, P. (2005). An efﬁcient algorithm to compute the land-

scape of locally optimal RNA secondary structures

with respect to the nussinov-jacobson energy model.

Journal of computational biology, 12(1):83101.

Debenedetti, P. G. and Stillinger, F. H. (2001). Su-

percooled liquids and the glass transition. Nature,

410(6825):259267.

Ding, Y.-S. and Zhang, T.-L. (2008). Using chous pseudo

amino acid composition to predict subcellular lo-

calization of apoptosis proteins: An approach with

immune genetic algorithm-based ensemble classiﬁer.

Pattern Recognition Letters, 29(13):1887–1892.

Dinis, L. (2008). Optimal sequence for parrondo games.

Physical Review E, 77(2):021124.

Dinis, L. and Parrondo, J. M. R. (2003). Optimal strate-

gies in collective parrondo games. Europhysics Let-

ters (EPL), 63:319–325.

Dins, L. and Parrondo, J. M. (2004). Inefﬁciency of voting

in parrondo games. Physica A: Statistical Mechanics

and its Applications, 343:701–711.

Doye, J. P. (2002). Network topology of a potential energy

landscape: A static scale-free network. Physical re-

view letters, 88(23):238701.

Fong, L. Y. and Szeto, K. Y. (2001). Rules extraction in

short memory time series using genetic algorithms.

The European Physical Journal B-Condensed Matter

and Complex Systems, 20(4):569572.

Goldberg, D. E. and Holland, J. H. (1988). Genetic al-

gorithms and machine learning. Machine learning,

3(2):9599.

Harmer, G. P. and Abbott, D. (1999). Game theory: Los-

ing strategies can win by parrondo’s paradox. Nature,

402(6764):864864.

Harmer, G. P. and Abbott, D. (2002). A review of

parrondos paradox. Fluctuation and Noise Letters,

2(2):R71R107.

Holland, J. H. (1975). Adaptation in natural and artiﬁcial

systems: An introductory analysis with applications to

biology, control, and artiﬁcial intelligence. U Michi-

gan Press.

Jiang, R., Szeto, K. Y., Luo, Y. P., and Hu, D. C. (2000).

Distributed parallel genetic algorithm with path split-

ting scheme for the large traveling salesman problems.

In Proceedings of Conference on Intelligent Informa-

tion Processing, 16th World Computer Congress, page

2125.

Messom, C. (2002). Genetic algorithms for auto-tuning mo-

bile robot motion control.

Parrondo, J. M. R. (1996). How to cheat a bad mathemati-

cian. EEC HC&M Network on Complexity and Chaos.

Parrondo, J. M. R., Dinis, L., Garca-Torao, E., and Sotillo,

B. (2007). Collective decision making and paradox-

ical games. The European Physical Journal Special

Topics, 143(1):39–46.

Patel, A. N., Davis, D., Guthrie, C. F., Tuk, D., Nguyen,

T. T., Williams, J., and others (2005). Optimiz-

ing cyclic steam oil production with genetic algo-

rithms. In SPE Western Regional Meeting. Society of

Petroleum Engineers.

Pond, S. L. K., Posada, D., Gravenor, M. B., Woelk, C. H.,

and Frost, S. D. W. (2006). GARD: a genetic algo-

rithm for recombination detection. Bioinformatics,

22(24):3096–3098.

Shiu, K. L. and Szeto, K. Y. (2008). Self-adaptive mutation

only genetic algorithm: An application on the opti-

mization of airport capacity utilization. In Intelligent

Data Engineering and Automated LearningIDEAL

2008, page 428435. Springer.

Szeto, K. Y. and Fong, L. Y. (2000). How adaptive agents in

stock market perform in the presence of random news:

A genetic algorithm approach. In Intelligent Data

Engineering and Automated LearningIDEAL 2000.

Data Mining, Financial Engineering, and Intelligent

Agents, page 505510. Springer.

Toral, R., Amengual, P., and Mangioni, S. (2003). Par-

rondo’s games as a discrete ratchet. Physica A: Statis-

tical Mechanics and its Applications, 327(1-2):105–

110.

Wagon, S. and Velleman, D. (2001). Parrondo’s para-

dox. Mathematica in Education and Research, 9(3-

4):8590.

Wales, D. J., Doye, J. P., Miller, M. A., Mortenson,

P. N., and Walsh, T. R. (2000). Energy landscapes:

from clusters to biomolecules. Advances in Chemical

Physics, 115:1112.

Wales, D. J., Miller, M. A., and Walsh, T. R.

(1998). Archetypal energy landscapes. Nature,

394(6695):758760.

Wu, D. and Szeto, K. Y. (2014). Extended parrondo’s game

and brownian ratchets: Strong and weak parrondo ef-

fect. Physical Review E, 89(2):022142.

Xia, C., Guo, P., Shi, T., and Wang, M. (2004). Speed con-

trol of brushless DC motor using genetic algorithm

based fuzzy controller. In Proceeding of the 2004

International Conference on Intelligent Mechatronics

and Automation, Chengdu, China, 3rd edn. A Treatise

on Electricity and Magnetism, volume 2, page 6873.

ApplicationsofGeneticAlgorithmonOptimalSequenceforParrondoGames