
Multi-goal Trajectory Planning with Motion Primitives for Hexapod
Walking Robot
Petr Van
ˇ
ek, Jan Faigl and Diar Masri
Department of Computer Science, Czech Technical University in Prague, Technick
´
a 2, 166 27 Prague, Czech Republic
Keywords:
Motion Planning, Traveling Salesman Problem.
Abstract:
This paper presents our early results on multi-goal trajectory planning with motion primitives for a hexapod
walking robot. We propose to use an on-line unsupervised learning method to simultaneously find a solution of
the underlying traveling salesman problem together with particular trajectories between the goals. Using this
technique, we avoid pre-computation of all possible trajectories between the goals for a graph based heuristic
solvers for the traveling salesman problem. The proposed approach utilizes principles of self-organizing map
to steer the randomized sampling of configuration space in promising areas regarding the multi-goal trajectory.
The presented results indicate the proposed steering mechanism provides a feasible multi-goal trajectory in a
less number of samples than an approach based on a priori known sequence of the goals visits.
1 INTRODUCTION
Walking robots provides a great flexibility to oper-
ate in complex unstructured environments. On the
other hand, motion planning for such a vehicle is chal-
lenging because of its high-dimensional configuration
space C. In this paper, we address a more challeng-
ing problem, where several optimal trajectories have
to be determined for a hexapod walking robot to re-
peatedly visit a given set of locations with a specified
precision. The problem is called the multi-goal mo-
tion planning (MGMP) and it combines challenges of
the motion planning together with challenges of the
combinatorial optimization as it is necessary to deter-
mine an optimal sequence of the goals visits together
with the cheapest trajectory connecting the goals.
The optimal sequence can be found as a solution
of the traveling salesman problem (TSP), which is
known to be NP-hard and efficient heuristics have
been proposed in operational research (Applegate
et al., 2007). However, the main computational dif-
ficulty lies in the determination of the particular tra-
jectories between the goals, which is a challenging
problem itself, e.g., PSPACE-hard (Reif, 1979) for a
polyhedral problem representation. For n goals, up
to n
2
goal–goal trajectories can be needed for a stan-
dard graph-based TSP solver. Moreover, this bound
does not hold for kinodymamic or non-holonomic
constraints, where it can be desirable to find a cost
efficient trajectory for a sequence of the goals.
(a) (b)
(c) (d)
Figure 1: Hexapod performing found multi-goal trajectory.
A trajectory between two goals can be found
by randomized sampling based motion planner, e.g.,
Rapidly-exploring Random Tree (RRT) and Rapidly-
exploring Random Graphs (RRG) (Karaman and
Frazzoli, 2011). However, a complex robotic platform
has a large set of possible control inputs, which does
not allow to efficiently use randomized planners with
all possible control inputs. Therefore, a set of motion
planning primitives can be considered for walking and
complex platforms (Bevly et al., 2000; Pivtoraiko and
Kelly, 2005). Motion primitives efficiently provide
only local motion, but they can be used in random-
ized planners, such as the RRT (Von
´
asek et al., 2013),
to find a global trajectory between two configurations.
599
Van
ˇ
ek P., Faigl J. and Masri D..
Multi-goal Trajectory Planning with Motion Primitives for Hexapod Walking Robot.
DOI: 10.5220/0005118405990604
In Proceedings of the 11th International Conference on Informatics in Control, Automation and Robotics (ICINCO-2014), pages 599-604
ISBN: 978-989-758-040-6
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

We propose to leverage on motion primitives and
steer the randomized sampling in the RRG to directly
find a solution of the multi-goal trajectory problem
for a hexapod walking robot without prior determina-
tion of the (optimal) sequence of the goals visits. The
idea is based on an on-line unsupervised learning on
top of the growing motion planning roadmap to con-
sider promising areas of C regarding the solution of
the sequencing part of the MGMP. Our early results
indicate the steering reduces the required number of
roadmap expansions to find an admissible multi-goal
trajectory and thus demonstrate feasibility of the pro-
posed approach for multi-goal trajectory planning.
The paper is organized as follows. The problem
is introduced in Section 2 together with description
of the considered robotic platform. A reference algo-
rithm for the MGMP problem for a given sequence
of the goals visits is presented in Section 3. The pro-
posed unsupervised learning based MGMP algorithm
is described in Section 4 and its validation in selected
case studies is presented in Section 5. The concluding
remarks and future work are summarized in Section 6.
2 PROBLEM STATEMENT
The MGMP problem is studied in a 3D environment
W ⊂ R
3
represented by a set of triangles forming a
set of obstacles O. The trajectory planning can be for-
mulated using the notion of the configuration space C.
Following (Karaman and Frazzoli, 2011), the simple
start–goal trajectory from a configuration q
init
to the
desired goal configuration q
goal
can be found as a mo-
tion query asking for a feasible path κ : [0,1] → C
f ree
such that κ(0) = q
init
and d(κ(1),q
goal
) < ε, where
C
f ree
denotes the obstacle free part of C as C
f ree
=
cl(C \ C
obs
), ε is an admissible distance of the trajec-
tory end-point to the desired goal, cl() is the closure
of a set, and d(,) is a distance between two configu-
rations.
Our motivational scenario is a visual inspection
planning problem to cover n given areas of interest
from particular locations G = {g
1
,g
2
,... ,g
n
}. We
assume each location is described by a 6D vector
R
3
× SO(3) consisting of a position (x,y,z) in W
accompanied by a desired orientation of the camera
pointing to the requested goal area denoted as (α,β,γ)
for roll, pitch, and yaw, respectively. We assume it
is sufficient the trajectory is within ε distance to the
goal location and provides a coverage of the area, i.e.,
a camera orientation is within particular angular lim-
its. For simplicity, we assume the camera is attached
at the center of the robot’s coordinate system and the
robot position is a 6D pose in W .
Similarly to a simple trajectory a multi-goal tra-
jectory visiting a set of goals G can be defined as
follows. Let the sequence of the goals visits be
(v
1
,v
2
,... ,v
n
) for which v
i
∈ G and
S
1<i≤n
v
i
= G.
Then, we can define the feasible and admissible multi-
goal trajectory as a closed trajectory τ : [0,1] → C
f ree
such that τ(0) = τ(1) = q
start
and for which there ex-
ists n points on τ such that 0 ≤ t
1
≤ t
2
≤ ... ≤ t
n
and
d(τ(t
i
),v
i
) < ε. In other words, there exists n points
from which the robot will cover the objects of interest.
Having these preliminaries, the MGMP problem
can be formulated as follows: for the given set of
goals G, configuration space C, admissible distance
ε, and monotonic, bounded, and strictly positive cost
function c: find a feasible and admissible (accord-
ing to ε) trajectory τ
∗
such that c(τ
∗
) = min{c(τ) |
τ is feasible admissible multi-goal trajectory}.
The proposed approach is based on the RRG al-
gorithm used for an incremental construction of the
graph G
RRG
=(V
RRG
,E
RRG
), which represents the mo-
tion planning roadmap constructed by the RRG algo-
rithm. The set of vertices V
RRG
represents particu-
lar configurations of the robot q ∈ C
f ree
and an edge
e ∈ E
RRG
describes a feasible motion between two
configurations v
i
,v
j
∈ V
RRG
,i 6= j. The graph is a re-
sult of the graph expansion from the nearest vertex
of the graph towards a random sample by applying a
particular control command from a considered set of
possible commands / motion primitives. The assump-
tions and specifications of the RRG for the considered
hexapod walking robot are described in the following
section.
2.1 RRG for Hexapod Walking Robot
The robotic platform considered in this study is 18
degrees of freedom (DoF) hexapod walking robot
(PhantomX), see Fig. 1. The body of the robot has
dimensions about 26 cm × 20 cm and its dimensions
with fully deployed legs are about 75 cm × 70 cm.
Motion planning for an 18 DoF platform can be com-
putationally demanding, and therefore, we consider
a set of motion primitives that significantly reduces
computational burden in randomized sampling based
motion planners for complex robots. The proposed
online-learning and steering of the randomized sam-
pling is general and does not assume a particular mo-
tion; however, we consider simple motion primitives
in this initial study because they allow more conve-
nient deployment and verification.
The used motion primitives allow crawling in for-
ward/backward, left/right, and diagonal direction and
crawling along a part of the circle with the defined ra-
dius. The primitives are designed in such a way that
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
600

they can be interchangeably shifted after finishing one
step, which allows a spread variety of combination
of motion patterns. Each primitive is parametrized
by a number of steps to be performed. The diagonal
crawling is parametrized by a direction angle from the
current state to the desired position, and curvature of
the circle for circular crawling. Thus, these primi-
tives allow the robot to perform 14 possible actions
that means 28 different motions.
For construction of the roadmap G
RRG
by the
RRG only a single parameter for each primitive is
used and the number of steps is set to 1. The length
of the particular motion step slightly differs and it is
around 10 ± 1 cm. Notice, the motion primitives re-
strict ability to reach an arbitrary configuration in few
RRG expansions. However, it provides a smooth tra-
jectory to reach vicinity of the desired goal locations.
In this study, we further simplify the problem by
considering robot motion on a plane. Besides, the
collision checking is computed using a bounding box
of the platform. These simplifications do not affect
the principle of the proposed steering but reduce the
computational burden. An additional speed improve-
ment is gained using goal bias and goal zooming tech-
niques (Lavalle and Kuffner, 2001) in sampling C
f ree
during expansion of the RRG.
3 REFERENCE MGMP
ALGORITHM
A simple multi-goal trajectory planner for a given se-
quence of goals visits is considered for a compari-
son with the proposed direct solution of the MGMP.
The planner represents a straightforward deployment
of the RRG algorithm for finding a multi-goal trajec-
tory. The required sequence of the goals visits can
be determined as a solution of the TSP, e.g., using the
CONCORDE solver (Applegate et al., 2003), with ap-
proximation of the goal–goal distances. The reference
planner follows the approach proposed in (Saha et al.,
2006) and Euclidean distances between the locations
are used for finding the sequence.
The reference algorithm is directly based on an in-
cremental construction of the roadmap G
RRG
by the
RRG. A robot starts at the position of the first goal g
1
,
which also initializes the roadmap. The goals from
the given sequence of locations (g
1
,... ,g
n
) are iter-
atively alternating to be the temporal goal q
t
of the
goal bias. After k
s
expansions with the same temporal
goal, the new one is altered. This is repeated until k
total expansions of the RRG. Then, for each goal g
i
∈
G the closest configuration q
i
= argmin
v∈V
RRG
d(v,g
i
)
is found. If the distance d(q
i
,g
i
) > ε the algorithm
fails; otherwise, the trajectory between q
i−1
and q
i
is
found and connected to the final trajectory τ. Finally,
the trajectory is enclosed connecting q
n
to q
i
. This
algorithm can provide a first admissible trajectory in
nk
s
RRG expansions and the trajectory can be then
further improved during the total of k expansions.
4 PROPOSED MGMP
ALGORITHM
The proposed multi-goal trajectory planner is based
on adaptation rules of the self-organizing map (SOM)
for the TSP (Faigl et al., 2011), which is a two lay-
ered neural network accompanied by an unsupervised
learning procedure. SOM provides a non-linear ap-
proximation of a high-dimensional input space into a
one dimensional output space that represents the re-
quested tour as a sequence of the output units. The
first layer is the input layer for presenting goals to
be visited and towards which the network is adapted.
The output layer consists of m units N = {ν
1
,... ,ν
m
}
representing neurons weights.
The unsupervised learning of SOM for the TSP
is performed in a series of learning epochs. At each
epoch, all goals to be visited are presented to the net-
work in a random order and for each goal the units
compete to be a winner using its distance to the pre-
sented goal. The winner node is then adapted to the
goal together with its neighbouring nodes. This learn-
ing procedure is repeated until each goal has a distinct
winner sufficiently close (e.g., in a distance less than
a given threshold δ).
The adaptation of neuron weights can be imagined
as a movement of the node closer towards the goal,
which may provide an intuitive insight to the learning
process. In our case, the neuron weights are particular
configurations in C and to ensure they are in C
f ree
, the
evolution of SOM is considered on a motion roadmap
G
RRG
constructed by the RRG. Thus, the weights are
restricted to be at the graph edges or vertices and the
adaptation can be imagined as movements of neurons
along the graph edges (Yamakawa et al., 2006). Once
the network is stabilized, the sequence of the goals
visits can be retrieved by traversing the output layer
and selecting associated goals to the winning units,
i.e., the closest unit to a graph vertex representing the
desired goal location v
g
∈ V
RRG
.
The fundamental issue of using SOM in MGMP
is that the selection of the winner node to a presented
goal g is based on computing a distance between node
ν and g. Such a distance corresponds to the length
of the trajectory from ν to g, which is obviously not
known due to a sparse coverage of C by G
RRG
. This
Multi-goalTrajectoryPlanningwithMotionPrimitivesforHexapodWalkingRobot
601

issue is addressed by new proposed approximation of
the distance, which together with the proposed adap-
tation turns out to a steering strategy for randomized
sampling in the RRG planner.
The approximation combines the Euclidean dis-
tance (e.g., as in (Englot and Hover, 2011)) with
the current knowledge about C stored in the incre-
mentally built roadmap G
RRG
. The current roadmap
should be used as much as possible, because it pro-
vides a realistic estimation about the expected dis-
tance d(ν,g). Therefore, a part of d(ν, g) is based
on a trajectory in G
RRG
from ν towards the vertex v
ν,g
that is found as
v
ν,g
= argmin
v∈V
RRG
(c(κ
ν,v
) + |(v,g)|), (1)
where c(κ
ν,v
) is the cost of the trajectory κ from ν to
v. A path P(ν,g) from ν to g consists of a trajectory
κ
ν,v
ν,g
in G
RRG
and a straight line segment (v
ν,g
,g)
from v
ν,g
to g as
P(ν,g) = κ
ν,v
ν,g
⊕ (v
ν,g
,g). (2)
On the other hand, the Euclidean distance between
two configurations would be always shorter or equal
to the length of the trajectory in G
RRG
, and therefore,
d(ν,v) has to respect the current knowledge of C and
the influence of the usually shorter Euclidean distance
should be suppressed. Therefore, we propose to com-
pute d(ν,g) for winner selection as
d(ν,g) = |P(ν,g)| = c(κ
ν,v
ν,g
) + |(v
ν,g
,g)|
2
. (3)
The adaptation modifies the neuron weights to get
a neuron closer to the goal. Thus, new weights ν
0
of the neuron after its adaptation represents a point
on the path P(ν,g) at the distance from ν defined by
the learning rules. The power of adaptation of winner
and its neighbors is controlled by the fractional learn-
ing rate µ and neighbouring function that has form
exp(−l
2
/σ
2
), where l is a distance of the node from
the winner and σ is called learning gain, which is de-
creased after each learning epoch. Therefore, the ex-
pected “traveled” distance of ν towards g is
|P(ν,g)| − |P(ν
0
,g)| = |P(ν,g)|µe
−l
2
/σ
2
. (4)
Such a new location can be out of the current roadmap
G
RRG
; however, we can consider the expected loca-
tion ν
0
as a temporal goal for expanding G
RRG
in k
a
iterations. Hence, ν
0
is used to steer the randomized
sampling in the RRG. After the expectation of G
RRG
,
ν
0
is restricted to be on an edge or vertex of G
RRG
to
guarantee the neurons weights always represent feasi-
ble and reachable configurations.
An intuitive insight to the learning procedure and
the final trajectory determination may arise from the
analyzing the situation at the final learning epochs.
The winners are closed to the goals, and therefore, a
trajectory from a neighbouring node to the goal will
likely go over the edge (or vertex) where the win-
ner node is located after the adaptation. Hence, the
roadmap graph G
RRG
is expanded to support determi-
nation of the final multi-goal trajectory by preferring
direction for expansion steered by the SOM evolution.
Completeness – Notice, the proposed procedure does
not affect the probabilistic completeness of the RRG.
It can be considered as a meta-heuristic strategy to
steer the randomized sampling towards the goals. The
unsupervised learning can be terminated at any time
and a regular RRG can be used to grow the roadmap
and find optimal trajectories between each consecu-
tive goals in the found sequence. Notice, the learn-
ing gain is decreased after each learning epoch, which
means the effective adaptation is terminated in a finite
number of learning epochs. Thus, the main purpose
of the unsupervised learning is to force sampling to
quickly find a feasible solution and also to determine
the sequence of the goals visits. These expectations
are verified for the robot motion model introduced in
Section 2.1 and our early results are presented in the
following section.
5 CASE STUDY
A validation of the proposed SOM based multi-goal
trajectory planner has been performed in two scenar-
ios to verify if the proposed steering strategy provides
a feasible multi-goal trajectory in less RRG expansion
steps than the reference method (denoted as MGMP
RRG) for the given sequence of goals. In the both
scenarios, the studied indicators of the planner per-
formance are the total number of RRG expansions
n
RRG
, the number of vertices and edges of the build
roadmap G
RRG
, and the required computational time
for the first feasible admissible multi-goal trajectory
that is closer than the selected ε to all goals. All the
presented results have been computed using a single
core of the iCore7 processor running at 3.4 GHz.
The used number of expansions k
a
in the SOM
RRG is 15 iterations for the winner and 10 iterations
are used for neighbouring nodes.
5.1 Influence of the Admissible Distance
The first evaluation is performed for a simple envi-
ronment, where the optimal sequence to visit 5 goals
can be determined using Euclidean distance. The en-
vironment is depicted in Fig. 4 where selected found
first feasible paths are visualized. Both algorithms
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
602
●
●
●
●
●
●
●
●
●
0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0 10000 30000 50000
ε [m]
Total no. of RRG Iterations
●
MGMP RRG
SOM RRG
(a) no.of RRG expansions
●
●
●
●
●
●
●
●
●
0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0 5000 10000 15000 20000
ε [m]
No. of Roadmap Vertices
●
MGMP RRG
SOM RRG
(b) no. of G
RGG
vertices
●
●
●
●
●
●
●
●
●
0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0 10 20 30 40
ε [m]
Path length [m]
●
MGMP RRG
SOM RRG
(c) trajectory length
●
●
●
●
●
●
●
●
●
0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09 0.1
0 1 2 3 4 5
ε [m]
CPU Time [s]
●
MGMP RRG
SOM RRG
(d) computational time
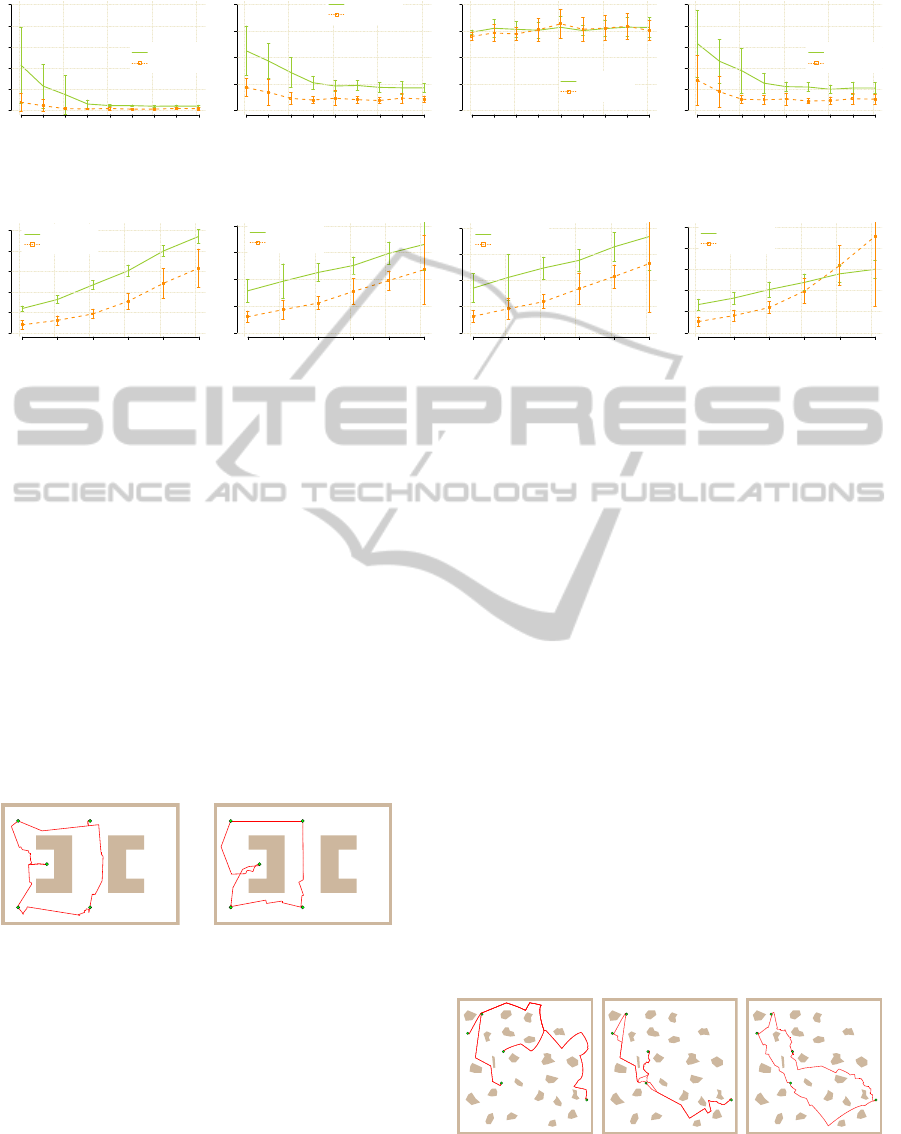
Figure 2: Average values of the studied indicators in simple MGMP problem with 5 goals and admissible distance ε.
●
●
●
●
●
●
5 7 10 13 17 20
0 2000 6000 10000
Number of Goals
Total no. of RRG Iterations
●
MGMP RRG
SOM RRG
(a) no. of RRG expansions
●
●
●
●
●
●
5 7 10 13 17 20
0 5000 10000 15000 20000
Number of Goals
No. of Roadmap Vertices
●
MGMP RRG
SOM RRG
(b) no. of G
RGG
vertices
●
●
●
●
●
●
5 7 10 13 17 20
0 5000 10000 15000 20000
Number of Goals
No. of Roadmap Edges
●
MGMP RRG
SOM RRG
(c) no. of G
RGG
edges
●
●
●
●
●
●
5 7 10 13 17 20
0 1 2 3 4 5
Number of Goals
CPU Time [s]
●
MGMP RRG
SOM RRG
(d) computational time
Figure 3: Average values of the studied indicators for the first feasible trajectory in potholes environment and number of goals.
RRG and SOM are randomized, and therefore, 50 tri-
als have been performed for each planner and the ad-
missible distance ε from the range 0.02 ≤ ε ≤ 0.1.
Notice, the reference planner uses the given se-
quence of the goals visits, while the SOM RRG ap-
proach also determines the sequence. Because of this,
it may happened that not the same sequence of the
goals visits as for the reference algorithms is deter-
mined. Therefore, only SOM MGMP solutions with
the identical sequence to the reference are considered.
The reference algorithms utilize k
s
= 200 RRG ex-
pansions for particular sampling towards the temporal
goal. In all cases, a feasible trajectory is found within
the given maximal number of RRG expansions, which
is set to 20 000.
(a) RRG, n
RRG
=2000 (b) SOM, n
RRG
=715
Figure 4: Found feasible solutions of the MGMP with 5
goals projected to a ground plan of the environment.
The average values of the studied indicators are
depicted in Fig. 2. Regarding the required n
RRG
to
find the first feasible multi-goal trajectory, the pro-
posed SOM based steering of the randomized sam-
pling requires the lowest number of the RRG expan-
sions. The main differences are for small ε, which
makes the problem more difficult for the randomized
planners with motion primitives.
A feasibility of the found multi-goal trajectories
has been experimentally verified for a real traversabil-
ity by the hexapod walking robot using the considered
motion primitives. Although the robot was controlled
in the open loop it was able to follow the planned tra-
jectory and reach all the desired goal locations. Snap-
shots form the deployment are depicted in Fig. 1.
5.2 Influence of the Number of Goals
In the second scenario, we study performance indica-
tors for increasing complexity of the underlying TSP
with the number of goals n ∈ {5,7,10,13,17, 20}. For
each n, 20 random instances have been created in the
environment called potholes that gives 120 problems
in total. A single value of ε = 0.1 m has been se-
lected and the number of RRG expansions was in-
creased to k
t
=500 and the total number of expansions
to k =50 000 for the MGMP RRG algorithm. Each
problem is solved 20 times, which gives 2400 trials
for both MGMP RRG and SOM RRG algorithms.
Here, SOM may provide different sequence of goals
visits more frequently, and therefore, we include all
sequences in the computation of the average values
of the studied performance indicators. The average
(a) n
RRG
=1 045 (b) n
RRG
=10 570 (c) n
RRG
=41 500
Figure 5: Found feasible solutions for 5 goals in potholes
environment: (a) the first feasible solution found by SOM
RRG; (b) evolved feasible SOM RRG solution; (c) refined
solution by the MGMP RRG.
Multi-goalTrajectoryPlanningwithMotionPrimitivesforHexapodWalkingRobot
603

values over all trials for the first found admissible tra-
jectories are shown in Fig. 3.
Also in this case, SOM RRG requires less num-
ber of RRG expansions to find a feasible solution.
Such a solution can be then improved by the RRG ex-
pansions in a similar way as the reference algorithm
works, which is demonstrated in Fig. 5.
5.3 Discussion
Despite of the relatively simple problems considered,
the presented early results validate a feasibility of the
proposed approach for steering the randomized sam-
pling in the RRG. The results indicate SOM for the
TSP can be applied directly in C and thus a construc-
tion of the motion planning roadmap prior sequenc-
ing part of the MGMP can be avoided. The SOM
RRG provides first feasible solutions of the MGMP
in fewer expansions steps albeit the quality of such a
solution is worse than for reference algorithm utiliz-
ing the known sequence of the goals.
The SOM based approach seems to be faster than
the reference algorithm in finding the first feasible so-
lution; however, we found out that the selection of the
winner node is computationally more demanding with
increasing learning epoch and the number of goals,
see Fig. 3(d). It is because the graph G
RRG
becomes
denser, which increases computational burden of the
determination of the vertex v
ν,g
by (1). This issue may
be addressed by removing non-perspective roadmap’s
vertices or by building an additional structure to sup-
port path queries in the roadmap.
6 CONCLUSION
In this paper, we address multi-goal trajectory plan-
ning with motion primitives and we introduce a new
steering strategy for randomized sampling in RRG to
improve its performance for a hexapod walking robot.
The proposed approach is based on principles of un-
supervised learning of self-organizing maps that al-
low to simultaneously solve the sequencing part of the
MGMP together with determination of the particular
trajectories. The presented early results of the pro-
posed idea in simple case studies provide a ground
work for a further research. Despite of the simple
problems considered, a straightforward MGMP plan-
ner based on a priori known sequence of goals visits
and the standard RRG algorithm requires more expan-
sion steps to find a feasible solution than the proposed
approach. This indicates that the proposed steering of
the randomized sampling in the RRG can improve the
performance of the planner significantly.
The encouraging results motives us to evaluate the
proposed idea in more complex problems and to com-
pare the performance regarding the solution quality
of the final multi-goal trajectory provided by other
approaches based on postponed distance evaluation
techniques.
ACKNOWLEDGEMENTS
The presented work is supported by the Czech Sci-
ence Foundation (GA
ˇ
CR) under research project No.
13-18316P. The work of Petr Van
ˇ
ek was supported by
the Grant Agency of the Czech Technical University
in Prague, grant No. SGS14/203/OHK3/3T/13.
REFERENCES
Applegate, D., Bixby, R., Chv
´
atal, V., and Cook, W. (2003).
CONCORDE TSP Solver. [cited 28 Feb 2012].
Applegate, D. L., Bixby, R. E., Chvatal, V., and Cook, W. J.
(2007). The Traveling Salesman Problem: A Com-
putational Study (Princeton Series in Applied Mathe-
matics). Princeton University Press.
Bevly, D., Farritor, S., and Dubowsky, S. (2000). Action
module planning and its application to an experimen-
tal climbing robot. In ICRA, pages 4009–4014.
Englot, B. and Hover, F. (2011). Multi-goal feasible path
planning using ant colony optimization. In ICRA,
pages 2255–2260.
Faigl, J., Kulich, M., Von
´
asek, V., and P
ˇ
reu
ˇ
cil, L. (2011).
An Application of Self-Organizing Map in the non-
Euclidean Traveling Salesman Problem. Neurocom-
puting, 74(5):671–679.
Karaman, S. and Frazzoli, E. (2011). Sampling-based algo-
rithms for optimal motion planning. Int. J. Rob. Res.,
30(7):846–894.
Lavalle, S. M. and Kuffner, J. J. (2001). Rapidly-Exploring
Random Trees: Progress and Prospects. Algorithmic
and Computational Robotics: New Directions, pages
293–308.
Pivtoraiko, M. and Kelly, A. (2005). Efficient constrained
path planning via search in state lattices. In Proceed-
ings of the 8th International Symposium on Artificial
Intelligence, Robotics and Automation in Space.
Reif, J. H. (1979). Complexity of the mover’s problem and
generalizations. In SFCS ’79: Proceedings of the 20th
Annual Symposium on Foundations of Computer Sci-
ence, pages 421–427. IEEE Computer Society.
Saha, M., Roughgarden, T., Latombe, J.-C., and S
´
anchez-
Ante, G. (2006). Planning Tours of Robotic Arms
among Partitioned Goals. Int. J. Rob. Res., 25(3):207–
223.
Von
´
asek, V., Saska, M., Kosnar, K., and Preucil, L. (2013).
Global motion planning for modular robots with local
motion primitives. In ICRA, pages 2465–2470.
Yamakawa, T., Horio, K., and Hoshino, M. (2006). Self-
Organizing Map with Input Data Represented as
Graph. In Neural Information Processing, pages 907–
914. Springer Berlin / Heidelberg.
ICINCO2014-11thInternationalConferenceonInformaticsinControl,AutomationandRobotics
604
