
Input-output Characteristics of LIF Neuron with
Dynamic Threshold and Short Term Synaptic Depression
Mikhail Kiselev
Applied Mathematics Dept. Chuvash State University, 428000 Cheboxary, Russia
Abstract. We consider a model of leaky integrate-and-fire neuron with dynam-
ic threshold and a very simple realization of short term synaptic depression
mechanism. Model simplicity makes possible creation of very large networks
on its basis. Required general properties of these networks can be obtained due
to the appropriate selection of neuron parameters. Knowledge of the depend-
ence of neuron firing frequency on presynaptic activity for various neuron pa-
rameters is crucial for this selection. Since this dependence cannot be obtained
in an exact analytical form we describe the process of building its empirical ap-
proximation using the multiple adaptive regression splines algorithm. This
methodology can be used for other neuron models.
1 Introduction
Spiking neural networks (SNNs), the most biologically realistic class of neural net-
work models, have one important distinctive feature. In contrast with more traditional
neural networks like perceptron which can perform non-trivial tasks even if it consists
of few dozen neurons only, practically applicable SNNs should include at least thou-
sands or more likely millions of neurons. It is an inevitable consequence of infor-
mation coding schemes used in SNNs and statistical nature of information processing,
learning and self-organization mechanisms inherent in them. It is clear that detailed
specification of all individual neuron properties, connections, synaptic weights is
impossible in big neuronal ensembles. Usually, only their basic large scale properties
like average number of excitatory and inhibitory connections, their mean strength, etc.
are specified, while detailed network configuration is generated randomly inside the
limits imposed by these large scale properties. Thus, as a rule, the simulated SNN is
originally chaotic and should obtain structure necessary for performing some desired
function due to self-organization process. One of the most important (and hardest)
questions to be answered for achievement of necessary network behavior is how to
select values of these basic network parameters. Naturally, it would be naïve to expect
that setting them randomly we will get a network with acceptable properties which
could demonstrate desired behavior after the respective evolution. Instead, it is most
probable, that it will either stay silent because of insufficient excitatory synapses
strength, or, on the contrary, show explosive total excitation growth to saturation lev-
el, or be involved in massive powerful oscillations suppressing any reaction to exter-
nal signals. Many other negative scenarios are possible… To avoid them it is crucial
to know relationship between properties of network as a whole and characteristics of
Kiselev M..
Input-output Characteristics of LIF Neuron with Dynamic Threshold and Short Term Synaptic Depression.
DOI: 10.5220/0005119700110018
In Proceedings of the International Workshop on Artificial Neural Networks and Intelligent Information Processing (ANNIIP-2014), pages 11-18
ISBN: 978-989-758-041-3
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

individual neurons and interneuron connections constituting it.
The most commonly used method for solution of this problem is based on the mean
field equations. In this approach neurons are characterized by their input-output char-
acteristics – the relationship between strength of stimulation of individual neuron and
strength of its response. It is assumed that stimulation of different synapses is com-
pletely uncorrelated and corresponds to Poisson process so that it can be described by
a single value - its total intensity (mean presynaptic spike frequency). More precisely,
we need to find relationship between the steady state firing frequency of neuron, its
parameters and the mean presynaptic spike frequency. This problem is not very diffi-
cult for simple leaky integrate-and-fire (LIF) neuron [1], but LIF neuron is too simple
to create realistic or functionally rich SNNs. For this reason, several more realistic
two-dimensional models have been proposed – like FitzHugh-Nagumo neuron [2] or
Izhikevich neuron [3]. The model considered in this paper is also two-dimensional (it
will be described formally in Section 2). It differs from LIF model by two features.
1. Dynamic threshold. Threshold value of membrane potential is incremented by a
constant each time the neuron fires and decays exponentially to its baseline level.
Models of this kind are described, for example, in [4]. It is an adaptive mechanism
which allows controlling maximum firing frequency.
2. Short Term Synaptic Depression (STD). It was experimentally demonstrated that
many types of synapses receiving high frequency spike train show different reac-
tion to individual spikes in the train. While the first spike causes significant change
of membrane conductance, effect of the subsequent spikes may be significantly
weaker. This phenomenon is described in many works [5, 6]. In fact, it is charac-
teristic for majority of synapses but in some kinds of synapses it is prevailed by the
opposite effect, short term synaptic facilitation. Due to STD the impact of one syn-
apse to neuron membrane potential value can be limited even in case when this
synapse receives very intensive stimulation. It is a very important feature because
neuron can perform non-trivial information processing only in case when it com-
bines signals from different sources. Many formal models of STD have been pro-
posed (see, for example [7]). As we will see in Section 2, the realization proposed
in this paper is very simple and is based on requirement that the total contribution
of one synapse to membrane potential is limited by a value proportional to the
weight of this synapse (the similar approach was used by me in [8, 9]).
Having described the neuron model in Section 2 we consider procedure of finding
its input-output characteristics in Section 3. In Section 4 we present and discuss the
final result. At last, Section 5 contains conclusion and ideas how the obtained result
could be utilized in further research.
2 Formal Neuron Model
Two main components of neuron state in our model are membrane potential u and
dynamic part of membrane potential threshold h. Membrane potential is rescaled so
that its rest value equals to 0 while firing threshold value after long period of inactivi-
ty is taken equal to 1. In general case the threshold value equals to
)0(1 hh
.
Thus, neuron fires when
hu
1 . Just after firing, the membrane potential is reset to
12

0 and dynamic threshold is incremented:
1;0
hhu .
(1)
While neuron is silent its dynamic threshold decays exponentially with the time con-
stant
h
which determines (together with other parameters) relative refractoriness
period of neuron.
The important feature of the considered model is dependence of synapse efficacy
on the history of presynaptic spikes coming to it, more precisely, on the time passed
since the most recent spike. To realize this dependence we introduce additional com-
ponents of neuron state
)10(
ii
vv , one value per synapse; here i denotes synapse
ordinal number. Just after reception of a new presynaptic spike by the synapse i its v
i
is set to 1. In the absence of presynaptic spikes, v
i
decay with the time constant
v
(the membrane potential decay time constant). When the neuron fires, all v
i
are reset
to 0. Value of v
i
determines contribution of the ith synapse to membrane potential:
ii
vwu
,
(2)
where w
i
is weight of the ith synapse ( 10
i
w ). Thus, effect of presynaptic spike
on membrane potential is less than w
i
if the same synapse received a presynaptic spike
some time t ago. In this case the membrane potential increment will be equal to
)exp(1
v
i
t
w
. Meaning of w
i
here is ratio of the maximum contribution of one
synapse to membrane potential to the baseline value of membrane potential threshold.
Possibly, this realization of STD is a bit oversimplified but it reaches its main goal –
to limit influence of a single synapse on neuron behavior even in case of its very
strong stimulation. Besides, it has another valuable feature. Namely, the standard
model of synaptic plasticity, STDP (spike timing dependent plasticity [1]), assumes
that LTP (long term synapse potentiation) value is determined by the time interval
between the most recent presynaptic spike obtained by the synapse and the postsynap-
tic spike emitted by the neuron. Therefore, synapses should store information about
most recent presynaptic spike. It is clear that the values v
i
in the discussed model rep-
resent the very convenient form of storing this information.
Thus, neuron state is characterized by values h and v
i
whose dynamics obeys the
following rules:
v
ii
h
v
dt
dv
h
dt
dh
, ;
1
i
v when the ith synapse receives spike;
if
i
ii
hvw 1
the neuron fires and
0,1
i
vhh .
(3)
Although this model is quite simple, the problem of finding its input-output charac-
teristics is far from being trivial, as we will see in next section.
13

3 Finding Input-output Characteristics
Thus, we would like to find dependence of the steady state neuron firing frequency F
on its properties and the frequency of presynaptic spikes f. In our model, neuron is
characterized by its time constants
v
and
h
, the number of synapses n and the syn-
aptic weights
)1( niw
i
. At first we consider case when the weights of all synap-
ses are equal to the same value w.
Unfortunately, as we will see, the assumption of equal value of all weights does not
help to formulate this dependence in a compact analytical form. It can be done only
for certain particular cases, for example, if f is very great. To analyze this case it is
convenient to imagine a very large ensemble of identical neurons stimulated by input
signal with identical characteristics and to consider the steady state values of h and v
i
averaged for the whole ensemble (v
i
-also for all synapses). We denote them as h
and
v
, respectively. Since the stimulation is very strong, the neurons fire very fre-
quently
h
F
1
and h is also great. Then its steady state value can be determined
from the equation
1))
1
exp(1(
h
F
h
,
(4)
which for great
h
F
yields
h
Fh
. Dynamics of mean value of membrane poten-
tial includes 3 factors:
1.
It grows due to incoming stimulation with the speed
)1( vfwn
per neuron.
2.
It decays with the speed
v
vwn
per neuron.
3.
It is reset to 0 in the firing neurons that gives decrease speed
h
FhFhF
2
)1(
per neuron.
Thus,
hh
v
FF
vwn
vfwn
22
)1(
.
(5)
The similar consideration of dynamics of
v
yields
vFvF
v
vf
v
)1(
.
(6)
Combining (5) and (6), we obtain quadratic equation for F:
wnffFF
h
)(
.
(7)
Unfortunately, in general case we have to deal with complex transcendental equa-
tions (for example, because we cannot get rid of the exponent in (4)). Therefore, if we
need analytical form of the input-output characteristics it can be only its approxima-
tion obtained by some method. I selected the most direct way - computer simulation
of the neuron model described by (3) and measurement of its firing frequency during
long time period. Since the model (3) is very simple it was easy to collect a large
14

dataset describing dependence of F on f for various values of
v
,
h
, n and w. After
that, I applied to this table one of the most powerful modern methods for automated
creation of non-linear regression models, multiple adaptive regression splines [10].
This procedure was carried out for the ranges of f,
v
,
h
, n and w, which can be
potentially biologically realistic. They are summarized in Table 1.
Since the parameter boundaries differ by several orders of magnitude it was more
convenient to work with their logarithms. It was also true for F because we needed to
minimize its relative rather than its absolute error. Inside these limits the values of
logarithm of parameters were chosen randomly and independently using uniform
distribution. Simulation time step was chosen equal to 1 msec. Every simulation ex-
periment corresponded to 1000 sec. The experiments where neuron did not fire at all
or fired with the mean frequency greater than 300 Hz were not considered. Results of
5223 experiments satisfying these conditions were gathered in a single table which
was loaded to the data mining system PolyAnalyst [11]. The empirical model ob-
tained on these data by the multiple adaptive regression splines module of PolyAna-
lyst system is discussed in next section.
4 Empirical Approximation of Neuron Input-output
Characteristics
Thus, as it was said, the method used to find dependence of F on f,
v
,
h
, n and w
was multiple adaptive regression splines. In order to avoid danger of overfitting the
complexity of the created model was limited by the following values. The maximum
number of basis functions was set equal to 100, the maximum basis function order –
to 3. The resulting formula itself cannot be inserted in the article (it would occupy
about 1.5 pages) – it can be obtained from me by request (for example, in form of C
code). While the model contains only few dozen degrees of freedom it appeared to be
quite precise (standard deviation = 0.243, R
2
= 0.971). Values of measured and pre-
dicted firing frequency are depicted on Fig. 1. We see that quality of data fitting is
very good everywhere except the region of very weak stimulation (< 1 Hz). However,
good approximation is hardly possible there because of strong signal fluctuations.
Examples of the input-output characteristics calculated using the obtained model
for different values of neuron parameters are shown on Fig. 2. We see that it is almost
linear in some cases, while in other cases this curve may have plateau and even be
non-monotonous. While negative val ue of derivative of this curve is a rare artefact,
Table 1. Ranges of Stimulation Intensity and Neuron Parameters for Which Neuron Firing
Frequency Was Measured.
Parameter Minimum value Maximum value
F 1 Hz 300 Hz
N 10 3000
W 0.01 0.3
v
3 msec 100 msec
h
1 msec 100 msec
15
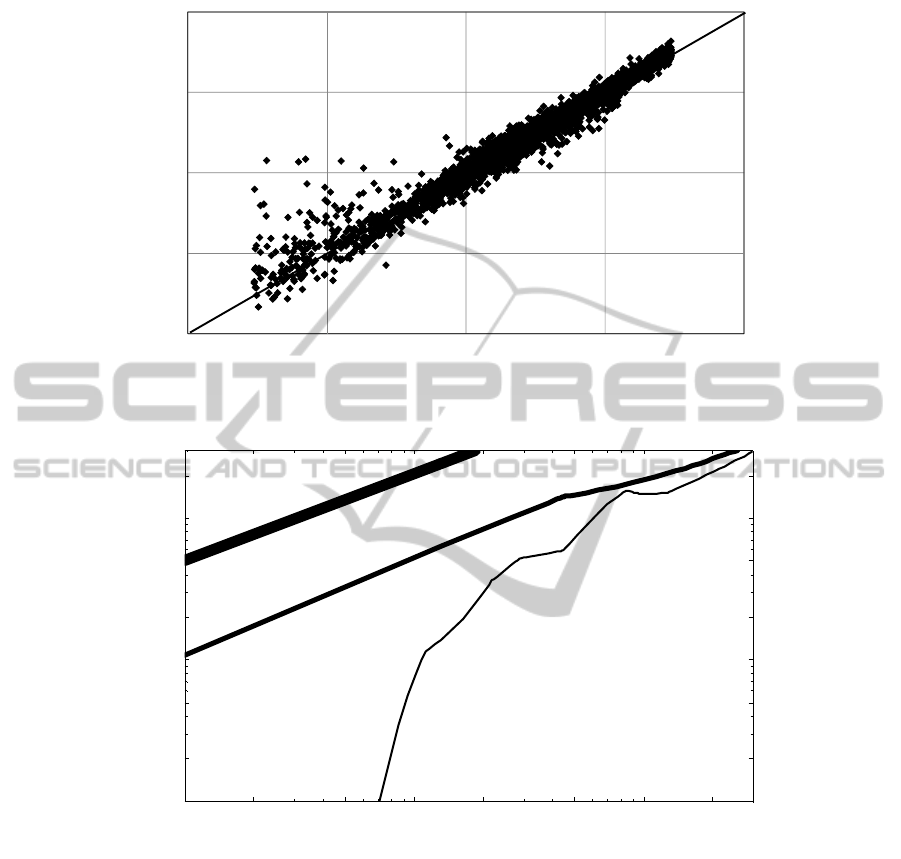
Fig. 1. Predicted vs. real values of neuron firing frequency.
Fig. 2. Empirical approximation of neuron input-output characteristics for different values of
neuron parameters. The thin line corresponds to
v
= 24.5 msec,
h
= 10 msec, n = 2032, w =
0.0348; the thick line – to
v
= 71 msec,
h
= 69 msec, n = 348, w = 0.0893; the very thick line –
to
v
= 36 msec,
h
= 8 msec, n = 68, w = 0.0467.
presence of plateau is explainable. In some circumstances increased stimulation may
have very weak impact on firing frequency because, at the same time, it leads to
growth of dynamic threshold. This situation is observed for thin line on Fig. 2 in case
of stimulation intensity close to 100 Hz. It illustrates why dynamic threshold may be a
useful stabilizing factor preventing uncontrolled excitation growth.
0,1
1
10
100
1000
0,1 1 10 100 1000
Predictedfiringfrequency,Hz
Measuredfiringfrequency,Hz
2 5 10 20 50 100 200
Stimulation, Hz
2
5
10
20
50
100
200
gniriFycneuqerf,zH
16

At last we should discuss how the obtained result could be extended to case of non-
uniform synaptic weight values. Since all input signals have identical properties and
are not correlated, the most important value determining the firing frequency is the
sum of all synaptic weights. Number of synapses plays its role only because it deter-
mines fluctuation magnitude in input stream, the fewer synapses, the stronger fluctua-
tions. But the process of transformation of presynaptic spikes to postsynaptic spikes
can be treated as information flow. Postsynaptic spikes contain information about
presynaptic spikes in form of conditional probabilities P
i
= P(postsynaptic spike |
presynaptic spike on the synapse i). But,
~
i
ii
i
w
Py
w
. Hence, the volume of this
information flow and, therefore, the magnitude of its fluctuations is determined by a
value proportional to
ii
yy log
. It follows from this discussion that for our pur-
pose neuron with n synapses having different weights w
i
can be approximated by
neuron with n* identical synapses with weight w*, where
ii
yyn log*log
,
(8)
i
w
n
w
*
1
*
.
(9)
5 Conclusion
In this paper, we considered a very simple model of spiking neuron which, despite its
simplicity, has a number of valuable properties. It can perform non-trivial information
processing in wide range of presynaptic signal intensity due to limitation of single
synapse contribution to membrane potential; it can help preventing uncontrolled exci-
tation growth due to dynamic threshold, and it is convenient for implementation of
STDP rule. Thanks to its simplicity, simulation experiments with large ensembles of
such neurons can be carried out. To predict general properties of these ensembles it is
crucial to know input-output characteristics of a single neuron. Since this characteris-
tics cannot be formulated in analytical form, we obtained its empirical approximation
collecting experimentally measured values of neuron firing frequency under various
conditions and processing these data using multiple adaptive regression splines algo-
rithm. The resulting empirical dependence can be included in the mean field equations
describing large neuronal ensembles for analysis of basic properties of their dynamics
(using respective numeric methods). It can also be utilized to evaluate acceptable
stimulation intensity range in simulation experiments and for other purposes. This
empirical law is an important component of numeric models of SNN dynamics used
in our ongoing research projects.
The described methodology for determination of neuron input-output characteris-
tics can be applied to other neuron models, as well, – in cases when it cannot be ob-
tained in exact analytical form.
17

References
1. Gerstner, W., Kistler, W.: Spiking Neuron Models. Single Neurons, Populations, Plasticity.
Cambridge University Press (2002)
2. Rocsoreanu, C., Georgescu, A., and Giurgiteanu, N.: The FitzHugh-Nagumo Model: Bifur-
cation and Dynamics. Kluwer Academic Publishers, Boston (2000)
3. Izhikevich, E. M.: Simple Model of Spiking Neurons. IEEE Transactions on Neural Net-
works. 14 (2003) 1569- 1572
4. Benda, J., Maler, L., Longtin, A.: Linear versus nonlinear signal transmission in neuron
models with adaptation currents or dynamic thresholds. Journal of Neurophysiology. 104
(2010) 2806-2820
5. Abbott, L. F., Varela, J.A., Sen, K., Nelson, S. B.: Synaptic depression and cortical gain
control. Science. 275 (1997) 220–224
6. Tsodyks, M., Pawelzik, K., Markram, H.: Neural networks with dynamic synapses. Neural
Comput 10 (1998) 821–835
7. Rosenbaum, R., Rubin, J., Doiron, B.: Short Term Synaptic Depression Imposes a Frequen-
cy Dependent Filter on Synaptic Information Transfer. PLoS Comput Biol 8(6): e1002557.
doi:10.1371/journal.pcbi.1002557 (2012)
8. Kiselev, M. V.: Self-organized Spiking Neural Network Recognizing Phase/Frequency
Correlations, Proceedings of IJCNN’2009, Atlanta, Georgia, (2009) 1633-1639.
9. Kiselev, M. V.: Self-organized Short-Term Memory Mechanism in Spiking Neural Net-
work, Proceedings of ICANNGA 2011 Part I, Ljubljana,(2011) 120-129.
10. Friedman, J. H.: Multivariate Adaptive Regression Splines. Annals of Statistics. 19, 1
(1991) 1-141
11. http://www.megaputer.com/site/polyanalyst.php
18
