A Holistic Seismic Risk Scheme Using Fuzzy Sets

Part One: The Social System Fragility

J. Rub

en Gonz

alez

Angela Nebot

, Francisco Mugica

, Martha-Liliana Carre

and Alex H. Barbat

IUSS UME School Via Ferrata 45, Pavia, Italy

Soft Computing Group, Technical University of Catalonia, Jordi Girona Salgado 1-3, Barcelona, Spain

International Center for Numerical Methods in Engineering, Technical University of Catalonia, Jordi Girona Salgado

1-3, Barcelona, Spain

Keywords:

Fuzzy Sets, Risk Management, Natural Hazards, Vulnerability Index, Social Vulnerability, Seismic Vulnera-

bility, Inference System.

Abstract:

Hazard related Risk is a strange concept since its represents something that has not happened yet, something

which is blur and randomness related. Along its estimation, social vulnerability aspects come to arise. Such

aspects are even more difﬁcult to deﬁne in part because there is still missing a robust way to quantify them

and, therefore, to establish a clear analytic framework useful to understand inherent complexities of a human

society. In this paper, we build a social aggravation coefﬁcient fuzzy model considering Cardona-Carre

aggravation descriptors. By reducing the number of aggravation descriptors and establishing fuzzy logic rules

between them, we found similar results in tendency and spatial distribution for seismic resilience and fragility

at Barcelona, Spain. We used a classical Mamdani fuzzy approach, supported by well established fuzzy theory,

which is characterized by a high expressive power and an intuitive human-like manner. We believe that in this

way, a more clear analyses of the resilience and fragility bond can be done exploiting in a more suitable way

fuzzy logic capabilities, because the inference process to obtain an aggravation coefﬁcient is based precisely

on the establishment of rules (if-then type) directly over the involved variables in social vulnerability formation

which allows a smooth application of risk management knowledge, encouraging debate over the used rules,

besides the discussion among the employed membership functions.

1 INTRODUCTION

Social vulnerability is one of the key factors to as-

sembly risk in space and time, however, such impor-

tant element is largely ignored over ex-ante, ex-post

and cost/lost estimation reports, in part because the

measurement of social vulnerability is not quite un-

derstood, and in part because the presence of epis-

temology oriented-based discrepancies along vulner-

ability deﬁnition, which binds a particular method-

ology with the orientation where such deﬁnition has

been used, i.e. ecology, human, physical, etc. There-

fore, there is a concept discrepancy when a social vul-

nerability model is about to be built. Diverse models

have been used to obtain social vulnerability estima-

tions. For example Cutter et al. (2003) used a haz-

ard of-place model to examine the components of so-

cial vulnerability to natural hazards among US coun-

ties through the development of a vulnerability index

based on the reduction of variables by a factor analy-

sis plus an additive model. Kumpulainen (2006) us-

ing ESPON Hazards integrative model, created a vul-

nerability index map for all Europe regions based on

an aggregated model, considering that regional vul-

nerability is measured as a combination of damage

potential (anything concrete that can be damage) and

the coping capacity. The principal difference between

these models rely on one basic deﬁnition: while in

Cutter’s model the hazard potential is dependent on

risk and mitigation, in ESPON model risk is a com-

bination of the same hazard potential and the regional

vulnerability.

Carre

no et al. (2012) proposed an seismic ag-

gravation risk model based on Cardona’s conceptual

framework of a risk model analysis for a city consid-

ering a holistic perspective, thus describing seismic

risk by means of indices (Cardona, 2001) and assess-

ing risk with the expression known as Mocho’s equa-

828

González R., Nebot À., Mugica F., Carreño M. and Barbat A..

A Holistic Seismic Risk Scheme Using Fuzzy Sets - Part One: The Social System Fragility.

DOI: 10.5220/0005129808280835

In Proceedings of the 4th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (MSCCEC-2014), pages

828-835

ISBN: 978-989-758-038-3

 2014 SCITEPRESS (Science and Technology Publications, Lda.)

tion in the ﬁeld of in the ﬁeld of disaster risk indica-

tors. They propose that seismic risk is the result of

physical risk (those elements susceptible to be dam-

age or destroyed) and an aggravation coefﬁcient that

includes both, the resilience and the fragility of a soci-

ety. Although the model was intended to be applied to

assess the risk over a city when it is strike by an earth-

quake, the structure of the social vulnerability module

of the model, (the one who deals with resilience and

fragility), can easily be transformed in a non-disaster

dependent analytic framework.

In this article, we propose a complete Mamdani

fuzzy aggravation model starting from the aggrava-

tion descriptors described in Carre

no et al. (2012).

The aggravation model synthesizes the social aggra-

vation characteristics of a city struck by an earthquake

that could conduct to social vulnerability enhance-

ment or moderation. A main advantage of the pro-

posed model is its white box nature that results in a

high level understandability model. Moreover, the

fuzzy approximation used in this paper is well stab-

lished and with solid background.

2 PREVIOUS MODELS

Many times the strength of a vulnerability model be-

comes weakened not because the type or resolution

of the models themselves but because the lack of in-

formation and accurate data, in such a way that the

results achieved are misleading in many ways

. Fur-

thermore, the lack on understanding about how accu-

rately measure vulnerability is one of the major un-

certainty sources among social models. In most of

the cases, social vulnerability is described using the

individual characteristics of people (age, race, health,

income, type of dwelling unit, employment, gross do-

mestic product (GDP), income, etc.) Just in recent

time, vulnerability models started to include place in-

equalities, such as level of urbanization, growth rates

and economic vitality (Carre

no et al., 2012).

Although there is a general consensus about some

of the major factors that inﬂuence social vulnerability,

disagreement arise in the selection of speciﬁc vari-

ables to represent these boarder concepts (Cutter et

al., 2003).

The proposed model by Cardona (2003) focus on

considering risk, as the possible economic, social and

environmental outcomes when a seismic might occur

over a period of time. Following a holistic approach,

Sometimes redirecting towards a deﬁnition staying that

vulnerability is a characteristic and not a condition, leading

towards the assumption that without damage, or a speciﬁc

hazard, vulnerability places could stand forever

Table 1: Descriptors used for aggravation estimation

(Carre

no et al., 2012).

AGGRAVATION DESCRIPTORS

Marginal Slums

Population Density

Mortality Rate

Delinquency Rate

Social Disparity

Hospital Beds

Human Health Resources

Emergency and Rescue Personnel

Development Level

Emergency Operability

the model puts in practice a multidisciplinary view,

which considers not only the expected physical dam-

age among infrastructures and structures, numbers of

victims and economic losses, but also those condi-

tions related with social fragility and lack of resilience

that can enhance the generation of second order ef-

fects, due the earthquake. Therefore, the variables

needs to address towards speciﬁc indexes or indica-

tors related with physical vulnerability, the suscepti-

bility of exposed elements to be damage considering

potential seismic intensities over a period of time, and

the context vulnerability which is dependent of social

fragility and lack of resilience of urban systems with

the potential to be harm because a disaster. The de-

scriptors used by (Carre

no et al., 2012) for aggrava-

tion estimation can be seen in the table 1.

2.1 Index Method

Carre

no et al. (2012) obtained a seismic risk evalu-

ation for Barcelona city by means of indicators that

leads to the calculation of a total risk index. This is

obtained by direct application of Moncho’s equation

described in 1:

= P

(1 + F) (1)

where R

is the total risk, P

is the physical risk and

F is a aggravation coefﬁcient.

Thus Carre

no’s model considers that seismic risk

is produced for both: physical and an aggravation co-

efﬁcient; this coefﬁcient provides an approximate vi-

sion of the state of the social capital infrastructure.

The F coefﬁcient depends on a weighted sum

of an aggravation factors set associated to socioe-

conomic fragility of the community (F

SFi

) and lack

of resilience of exposed context (F

LR j

), according to

equation 2.

F =

∑

i=1

SFi

∑

i=1

LR j

(2)

AHolisticSeismicRiskSchemeUsingFuzzySets-PartOne:TheSocialSystemFragility

829

where w

SFi

and w

LR j

are the assessed weights on each

factors calculated by an analytic hierarchy process

(Carre

no et al., 2007; Saaty and Vargas, 1991), and m

and n the total number of descriptors, of fragility and

lack of resilience, respectively. The descriptors of the

socioeconomic fragility and lack of resilience of ex-

posed context where obtained from existent databases

and statistical data for the studied area.

One of the issues arising from Moncho’s equation

is the consideration that F can be up to much twice the

value of P

, which is not always accomplished, be-

cause some times the indirect effects are much larger

than the direct effects, leading a mislead in risk esti-

mation.

2.2 Carre

no’s Fuzzy Method

Taking the objective of build a more ﬂexible risk man-

agement tool when information is incomplete or is not

available, Carre

no et al. proposed the use of fuzzy

logic tools and expert opinion to replace indexes by

fuzzy sets. The same descriptors are used and the se-

quences of calculations are similar to those made in

the caonventional index method, however the aggra-

vation’s descriptors values which were originally ob-

tained by demographic data bases are replaced by lo-

cal expert opinions. Using linguistic qualiﬁers, in-

stead of using numerical values, the aggravation value

can be evaluated. Distinct linguistic descriptors qual-

iﬁers where proposed, which range in 5 levels of ag-

gravation description: very low, low, medium, high,

very high. Using local expert opinion, a membership

function was deﬁned for each linguistic level used to

link the reported demographic or expert opinion value

to one level of aggravation.

With the positive link between a reported data and

its suitable linguistic level, the level is then grouped

into another set of membership functions, (based on

expert opinion or strictly arbitrary) which plays as

a homogenizer since it blends the original qualiﬁer

level into a new single fuzzy set.

They calculated the fuzzy union between so-

cial fragility and lack of resilience descriptors,

, x

), and applied on each of these new mem-

bership functions, µ, the weights, w, corresponding to

the level of aggravation, L

, of each descriptor x

SFi

and x

LR j

, as deﬁned in equation 3.

, x

) = max (w

SF1

FL1

)...w

LR1I

FLI

))

(3)

The proposed weighted and union methods be-

tween social fragility and lack of resilience descrip-

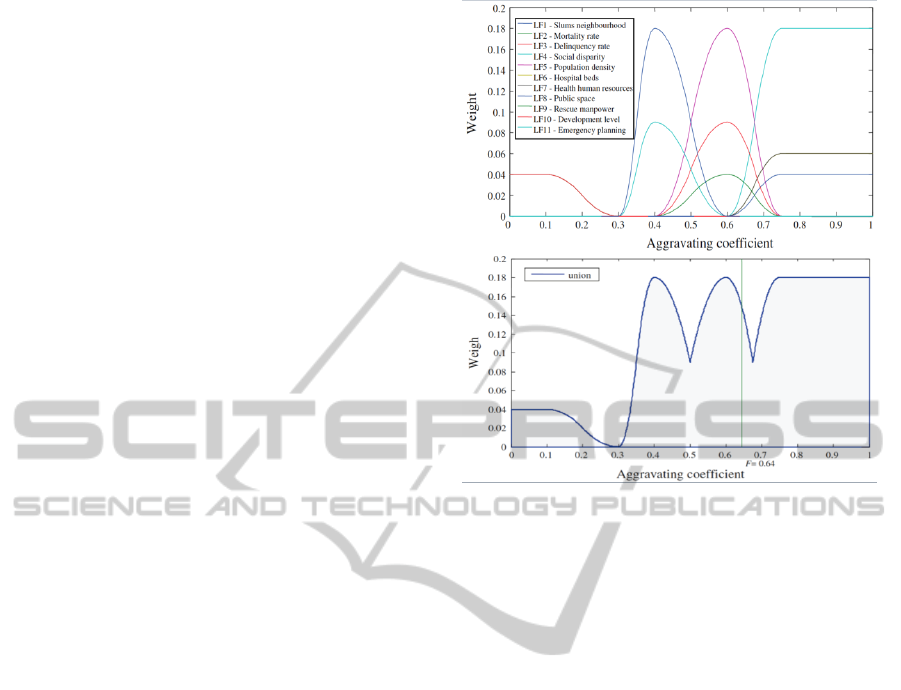
tors can be seen in Figure 1.

In the same way of index’s method, weights are

Figure 1: Carre

no weighting (up) and union method (low)

for San Mart

ı District, Barcelona Spain (taken from Carre

et al., 2012).

assigned to each fuzzy set by using an analytic hier-

archy process. The aggravation coefﬁcient F is cal-

culated as the centroid abscise of the area beneath the

curve obtained with Equation 3.

We think that the Carre

no’s fuzzy model presented

in this section is not entirely appropriate because it

is a non-conventional fuzzy approach, which may be

questionable due to the fact that fuzzy mathematical

raised in the inference process is not well established

and accurately validated.

3 CLASSICAL FUZZY METHOD

The model proposed in this research pretend to build

the same aggravation coefﬁcient by re-deﬁning their

variables into three different Fuzzy Inference Systems

(FIS), called: resilience, fragility and aggravation.

Each subsystem is deﬁned by a set of rules directly

over the aggravation descriptors. A conceptualiza-

tion of the different steps along the proposed model

can be seen in Figure 2. The variables involved in

each subsystem are presented in the left hand side of

Figure 2. FIS #1, corresponds to the Fragility model

and has as input variables the Marginal Slums (MS),

the Social Disparity Index (SDI) and the Population

Density (PD). The output of FIS #1 is the level of

Fragility. On the other hand, FIS #2 corresponds to

the Resilience model and has as input variables the

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

830

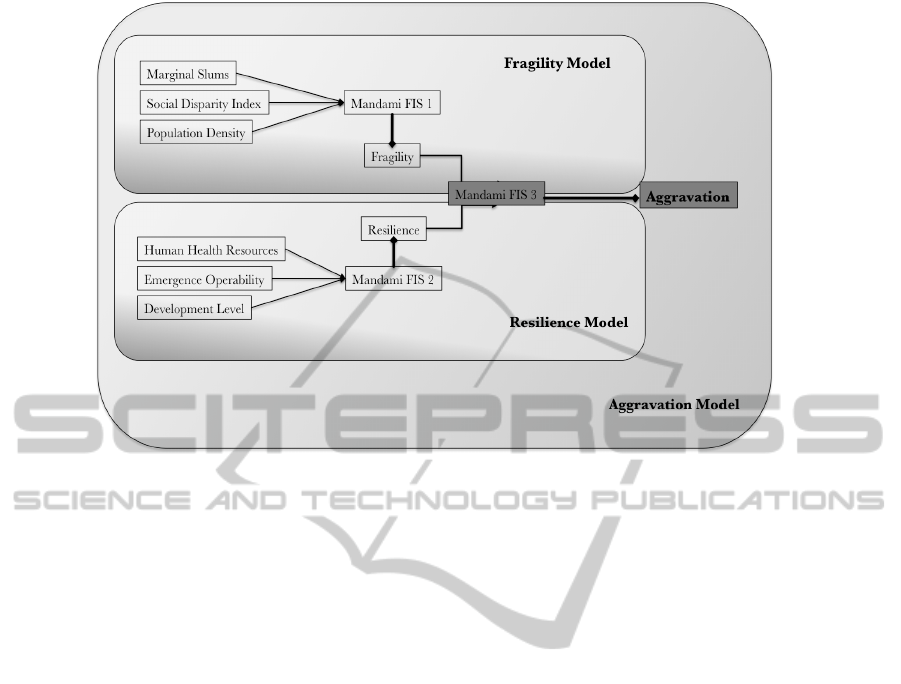
Figure 2: Conceptualization of Fuzzy Classical Model to estimate Aggravation Coefﬁcient.

Human Health Resources (HHR), the Emergency Op-

erability (EO) and the Development Level (DL). The

output of FIS #2 is the Resilience level. The Aggra-

vation model (FIS #3) takes as inputs the fragility

and resilience levels that are the output of FIS #1

and #2, respectively, and infers the aggravation co-

efﬁcient. All the fuzzy inference systems proposed

in this research are based on the Mamdani approach

(Mamdani and Assilian, 1975), since it is the one that

better represents the uncertainty associated to the in-

puts (antecedents) and the outputs (consequents) and

allows to describe the expertise in an intuitive and

human-like manner. Our main objective is to develop

a fuzzy aggravation model as much interpretable as

possible and with high expressive power. In our ap-

proach the original ten variables presented in Table 1

are reduced to six variables. Population density, Slum

area or marginal slums, Human health resources and

Development level remain the same, and Social dis-

parity index and Emergence operability are redeﬁned

in such a way that subsume the other variables. The

reduction or simpliﬁcation of the original variables

was made by taking advantage of certain descriptors

that are linked and could englobe various descriptors

in one single class considering its social nature, for

example: the descriptors called: mortality rate and

delinquency rate, are related between them and are

reﬂecting social consequences produced by a social

structure failure (could be lack of access) to certain

social advantages, such as having an efﬁcient public

health program, or no marginalization dynamics, or

access to education and effective justice and law poli-

cies. Therefore we consider these descriptors could

be enclosed within the descriptor called social dispar-

ity index, which is a fragility descriptor as well. In

the case of resilience descriptor we merge descriptors

called: Public Space, Hospital beds, and Emergency

Personnel, into the descriptor called Emergence Op-

erability, because the former descriptors acts when

the emergency is being or has recently occurred, and

therefore are related with the capacity of the city to

face an emergence situation, and the assets that a city

has to confront it. We modify fuzzy classes by reduc-

ing the number of linguistic levels deﬁned for each

descriptor up to 3 (low, medium, high) along their re-

spective universe of discourse, but we kept the same

ﬁve levels for the ﬁnal output (resilience, fragility

and aggravation). We think that 3 classes is enough

to represent accurately the input variables of the re-

silience and fragility models. Moreover, a reduction

of the number of classes implies also a more com-

pacted and reduced set of fuzzy rules. In the same

way, to improve model’s sensibility, we adjust mem-

bership functions forcing them to be more data-based

kind of type, thus considering the reported aggrava-

tion data as embedded along membership functions

limits deﬁnition. With these new membership func-

tions we build a set of fuzzy logic rules that could in-

fer the behaviour of the aggravation coefﬁcient com-

ponents using the three Mamdani Fuzzy Inferences

Systems mentioned before (see Figure 2).

The developing of the fuzzy rules was established

for consider all possible combinations between the

input descriptor’s linguistic levels, giving a total of

AHolisticSeismicRiskSchemeUsingFuzzySets-PartOne:TheSocialSystemFragility

831

Table 2: Logic Rules used for resilience estimation.

HHR=Human Health Resources, DL= Development Level,

EO=Emergency Operability, R = Resilience, VH = Very

High, H = High, M = Medium, L= low, VL = Very Low

If (HHR is L) and (DL is L) and (EO is L) then (R is VL)

2. If (HHR is M) and (DL is M) and (EO is M) then (R is M)

3. If (HHR is H) and (DL is H) and (EO is H) then (R is VH)

4. If (HHR is M) and (DL is L) and (EO is L) then (R is L)

5. If (HHR is H) and (DL is H) and (EO is L) then (R is M)

6. If (HHR is L) and (DL is M) and (EO is L) then (R is L)

7. If (HHR is M) and (DL is M) and (EO is L) then (R is M)

8. If (HHR is H) and (DL is M) and (EO is L) then (R is H)

9. If (HHR is L) and (DL is H) and (EO is L) then (R is M)

10. If (HHR is M) and (DL is H) and (EO is L) then (R is M)

11. If (HHR is H) and (DL is H) and (EO is L) then (R is H)

12. If (HHR is L) and (DL is L) and (EO is M) then (R is L)

13. If (HHR is M) and (DL is L) and (EO is M) then (R is M)

14. If (HHR is H) and (DL is L) and (EO is M) then (R is H)

15. If (HHR is L) and (DL is M) and (EO is M) then (R is M)

16. If (HHR is H) and (DL is M) and (EO is M) then (R is H)

17. If (HHR is L) and (DL is H) and (EO is M) then (R is M)

18. If (HHR is M) and (DL is H) and (EO is M) then (R is H)

19. If (HHR is H) and (DL is H) and (EO is M) then (R is H)

20. If (HHR is L) and (DL is L) and (EO is H) then (R is M)

21. If (HHR is M) and (DL is L) and (EO is H) then (R is H)

22. If (HHR is H) and (DL is L) and (EO is L) then (R is H)

23. If (HHR is L) and (DL is M) and (EO is H) then (R is H)

24. If (HHR is M) and (DL is M) and (EO is H) then (R is VH)

25. If (HHR is H) and (DL is M) and (EO is H) then ((R is VH)

26. If (HHR is L) and (DL is H) and (EO is H) then (R is H)

27. If (HHR is M) and (DL is H) and (EO is H) then (R is VH)

27 rules for calculating fragility and resilience val-

ues respectively. The rules were intended to follow

risk management literature which could suggest pos-

sible outcomes when three of these elements interact

to form resilience or fragility. The Mamdani aggrava-

tion model, that has as input variables the resilience

and the fragility, discretized into 5 classes each, is

composed of 25 fuzzy rules. In Table 2 the rules of the

Mamdani resilience model are presented as an exam-

ple. As mentioned before, the use of classical fuzzy

systems, with well established fuzzy inference theory,

allow a high level understandability model, easily un-

derstandable by experts which leads towards a deepest

discussion in the topic of social vulnerability descrip-

tion and casual interrelation.

Let’s describe the inference process by follow-

ing the example of the proposed Resilience FIS. The

fuzzy inference engine combines the fuzzy if-then

rules (see Table 2) into a mapping from fuzzy sets

in the input space U ⊂ R

to fuzzy sets in the output

space V ⊂ R, based on fuzzy logic principles.

Let’s U = U

x U

⊂ R

and V ⊂ R, where

, U

and U

represents the universes of discurse of

Marginal Slums, Social Disparity Index and Popula-

tion Density input variables, respectively, and V the

universe of discourse of Resilience. In hour case each

input variable contains three fuzzy sets and the output

variable is discretized into ﬁve fuzzy sets. Then, the

fuzzy rule based shown in Table 2 can be expresed in

a canonical form as shown in Equation 4.

(l)

: IFx

isA

and...andx

isA

T HENyisB

(4)

where A

and B

are fuzzy sets in U

and V , respec-

tively, x = (x

, x

) ∈ U are Marginal Slums, So-

cial Disparity Index and Population Density linguistic

variables, y ∈ V is the Resilience linguistic variable

and l = 1, 2, ..., 27 is the rule number. Consider now

the fuzzy facts: x

is A

, x

is A

, x

is A

, being A

, A

and A

fuzzy sets.

The Generalized Modus Ponens allows the deduc-

tion of the fuzzy fact y is B

by using the compo-

sitional rule of inference (CRI), deﬁned trough the

fuzzy relation between x and y, as deﬁned in Equa-

tion 5.

= A

◦ R (5)

where A

= (A

, A

). The simplest expression of

the compositional rule of inference can be written as

Equation 6.

(y) = I (µ

), µ

(y)) (6)

when applied to the ith-rule; where:

) = T



), µ

)



where x

= (x

, x

). Here, T is a fuzzy conjuctive

operator and I is a fuzzy implicator operator.

Once the inference is perfromed by means of the

compositional rule of inference scheme, the resulting

individual (one for each rule) output fuzzy sets are

aggregated into an overall fuzzy set by means of a

fuzzy aggregation operator and then a defuzziﬁcation

method is employed to transform the fuzzy set into a

crisp output value, i.e. the resilience level following

the example. The defuzziﬁcation method used in this

work is the Centre Of Gravity (COG), which slices

the overall fuzzy set obtained in the inference process

into two equal masses. The centre of gravity can be

expressed as Equation 7.

COG =

xµ

(x)dx

(7)

where B is fuzzy set on the interval [a, b].

In this research, this Mamdani fuzzy inference

process is used for both descriptors, i.e. fragility and

resilience. Once the evaluation has been made for

both descriptors, it’s possible to calculate the aggra-

vation coefﬁcient using the Aggravation fuzzy infer-

ence system (see Figure 2). The antecedents in this

case are the resilience and fragility descriptors and the

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

832

consequent is the aggravation coefﬁcient. The crisp

value for the aggravation coefﬁcient was obtained also

trough the calculation of COG. For comparison pur-

poses and following Carre

no’s fuzzy previous work,

the obtained aggravation value is then used to evalu-

ate aggravation’s linguistic level, in order to perform

a graphical representation of the levels of aggravation

in each district, as presented in the next section.

In absence of a defensible method for assigning

weights for social vulnerability estimators (Cutter,

2003), and contrarily to Carre

no’s fuzzy approach, we

did not made any a priori assumption about the im-

portance of each factor in the overall behaviour of the

system. In this way, each factor was viewed as having

an equal contribution to the fragility or resilience con-

ﬁguration. In this way it becomes possible to study

the importance of the weights assigned in previous

works when evaluating an aggravation coefﬁcient.

4 RESULTS AND COMPARISON

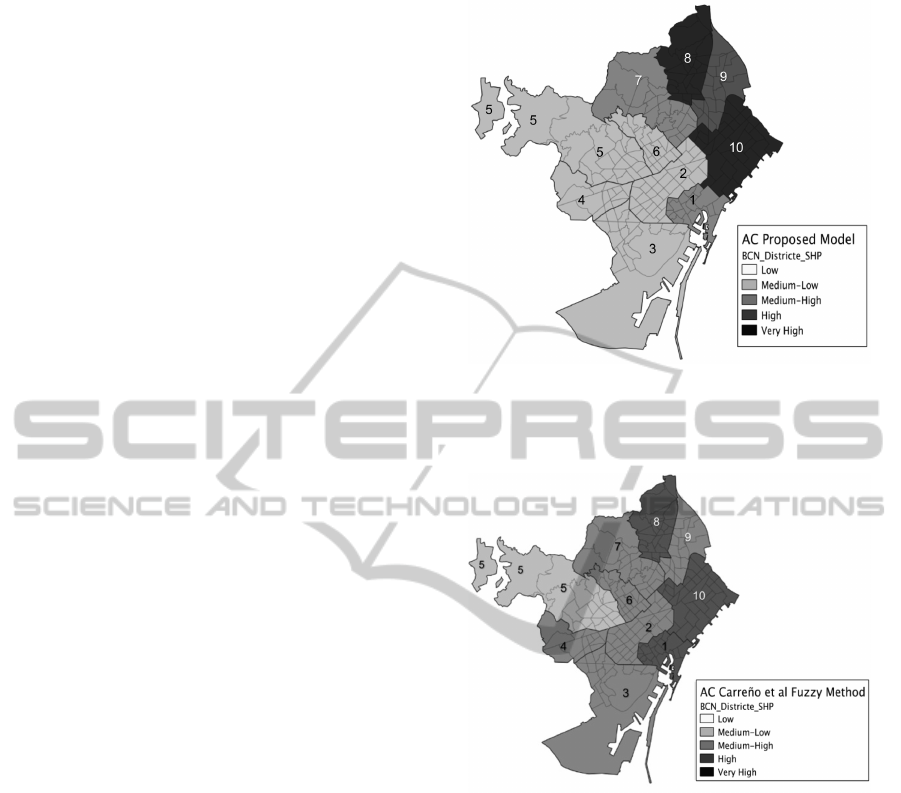
Figure 3 shows the estimated spatial distribution of

the aggravation coefﬁcient and its correspondent level

for the 10 administrative districts, of the city of

Barcelona, achieved through the proposed model.

Figures 4 and 5 show the aggravation coefﬁcient cal-

culated by Carre

no et al. using fuzzy sets or index

methods, respectively.

The proposed model, equal than the two alterna-

tive methods, estimates that highest aggravation is

spread mostly over the northeast part of the city. In

our model, levels of very high are reached over Sant

Mart

ı and Nou Barris district, high for San Andreu,

medium-high values for Horta-Guinard

o and Ciutat

Vella, while the rest of the city presents values of

medium-low aggravation level.

As we can see in Figure 4, Carre

no’s fuzzy method

considers that most of the city aggravation coefﬁcient

ranges between medium-low and medium-high levels,

while index method and our proposed method resem-

ble similar value levels (medium-low) thus not over-

estimating aggravation.

Figures 6, 7 and 8 show the aggravation coefﬁ-

cient numerical value obtained by the proposed fuzzy

model, the index model and Carre

no’s fuzzy model,

respectively. Districts are ordered from lower to high-

est aggravation level. In these ﬁgures we can see that

even there is no correct total match among the three

methods, all of them preserve quite the same order in

terms on higher and lower aggravation levels. When

comparing the numerical aggravation value obtained

from both fuzzy models (Carre

no’s fuzzy model and

the proposed model) to a robust method like index

Figure 3: Aggravation Coefﬁcient. Proposed Model: (1)

Ciutat Vella, (2) Eixample, (3) Sants-Montjuic, (4) Les

Corts, (5) Sarri

a-Sant Gervasi, (6) Gr

acia, (7) Horta-

Guinard

o, (8) Nou Barris, (9) Sant Andreu, (10) Sant Mart

ı.

Figure 4: Aggravation Coefﬁcient. Carre

no et al fuzzy

method: (1) Ciutat Vella, (2) Eixample, (3) Sants-Montjuic,

(4) Les Corts, (5) Sarri

a-Sant Gervasi, (6) Gr

acia, (7) Horta-

Guinard

o, (8) Nou Barris, (9) Sant Andreu, (10) Sant Mart

ı.

models (Marulanda et al., 2009), both suffer a slight

under and overestimation of the aggravation values by

district. In the proposed method this issue could be

addressed with the inclusion of weights to each de-

scriptor, as the other methods do. Nevertheless, we

consider that even with these small numerical dissim-

ilarities, the proposed fuzzy model limits the differ-

ent aggravation levels in a suitable way, allowing the

identiﬁcation of more potentially problematic zones

with a good resolution and reduced computation time.

Figure 9 shows the same as Figures 6, 7 and 8 but

without ordering the districts by aggravation value,

showing how the aggravation values behaves along

the different districts. As it can bee seen, even if the

explicit aggravation coefﬁcient value is not the same

AHolisticSeismicRiskSchemeUsingFuzzySets-PartOne:TheSocialSystemFragility

833

Figure 5: Aggravation Coefﬁcient. Index Method: (1) Ciu-

tat Vella, (2) Eixample, (3) Sants-Montjuic, (4) Les Corts,

(5) Sarri

a-Sant Gervasi, (6) Gr

acia, (7) Horta-Guinard

o, (8)

Nou Barris, (9) Sant Andreu, (10) Sant Mart

ı.

Figure 6: Aggravation Coefﬁcient values by district, Pro-

posed Fuzzy Model.

for each district, a similar trend shape come to appears

(with the inherent over and underestimation aggrava-

tion level), which leads to the conclusion that the gen-

eral behaviour of the proposed model is coherent with

the other two mentioned models.

4.1 Discussion

According to the previous analysis, with the use of

classical fuzzy inference system methodology it is

plausible to reproduce the results obtained from a

more analytical method such as indexes, for exam-

ple: in terms of district aggravation classiﬁcation, or

in reproducing similar spatial pattern of aggravation.

In ﬁrst term, the proposed inference model allows a

useful simpliﬁcation for the large quantity of vari-

Figure 7: Aggravation Coefﬁcient values by district, Index

Model.

Figure 8: Aggravation Coefﬁcient values by district,

Carre

no’s Fuzzy Model.

ables required for social aggravation analysis, in the

spirit of reduce the subjectivity associated with ag-

gravation descriptors suitability designation by using

a more ﬂexible and small descriptors set in which

the underlying links between them can be more eas-

ily observed, enabling a more understandable anal-

ysis scheme for social aggravation inference estima-

tion. Building rules directly over the aggravation de-

scriptors allows to assemble a compositional rule of

inference over the very same descriptors that are as-

sumed to create aggravation itself, therefore the infer-

ence process can be made using rules designed to fol-

low risk management knowledge, allowing the model

to represent, with a certain degree of freedom, the ac-

tual understanding of aggravation formation, and at

the same time, it allows a real discussion of the rule’s

structure strength; which can be absolutely improved

with a deepest debate.

SIMULTECH2014-4thInternationalConferenceonSimulationandModelingMethodologies,Technologiesand

Applications

834

Figure 9: Aggravation coefﬁcient comparison over the 10

Barcelona Districts.

Fuzzy logic inference capabilities can be exploited

in a more suitable way because the outputs from each

FIS used in the model are always fuzzy sets, giving

the chance to connect them trough a new FIS without

loosing consistency, allowing model completeness.

At the other hand, the proposed model slightly

over and underestimated aggravation values for some

districts when comparing with index model, as it is

also de case of Carren

o’s fuzzy model. However, if

necessary, the proposed fuzzy model can be further

tuned if descriptors are weighted.

4.2 Future Work

The ﬂexibility of the model enables its adaptation to

several conditions which could be used in more gen-

eral studies of social vulnerability and that can also

help to ﬁll some gaps among analytic methods. For

example, the same procedure can be applied to a more

general social vulnerability model that considers not

only physical, and aggravation inputs, but environ-

mental, economic and even completely subjective de-

scriptors can be add as well, such as solidarity or

brotherhood

. All of these can then be embedded into

one single inference model. One of the main prob-

lems of risk ex-ante and ex-post models is that they

don’t necessarily consider the interconnectivity of so-

cial characters (sectors) in a real scenario, for exam-

ple, the lack of hospitals in one geographic area does

not necessarily mean that human health resources is

zero at that place. It will be like assuming that the

ﬁre department can only help those who are in close

proximity. Assuming interconnectivity, the potential

damage to the social network-connections in case of

Loosing in this way its event-base model characteriza-

tion.

disaster is the real issue that must be addressed, and

we consider it plausible to be approach using fuzzy

methods.

5 CONCLUSIONS

We obtain a inference fuzzy model to make an esti-

mation of social aggravation over Barcelona city us-

ing the descriptors proposed in (Carre

no et al., 2012).

Building inference compositional rules over the se-

lected descriptors, we were able to obtain a robust

method that resembles the identiﬁcation of relevant

aspects and characteristics of seismic risk of cities al-

ready achieved by two other consolidated methods.

The proposed model displays more simplicity, ﬂex-

ibility and resolution capacities and can be rapidly

transformed into a non-disaster event model type with

the inclusion of new type of variables, englobing a

more detailed social vulnerability scheme and inter-

connectivity issues.

REFERENCES

Cutter, S. L., Boruff, B. J., Shirley, W. L., (2003) Social

Vulnerability to Environmental Hazards. Social Sci-

ence Quarterly,84.

Cardona, O. D., (2001), Holistic evaluation of the seis-

mic risk using complex dynamic systems (in Span-

ish), PhD Thesis Technical University of Catalonia,

Barcelona, Spain.

Cardona, O. D., (2003), The need for rethinking the con-

cepts of Vulnerability and Risk from an Hollistic Per-

spective: a necessary review a criticism for effective

Risk Management, Mapping Vulnerability: Disasters,

Developing and People Chapter 3 Earthscan Publish-

ers, London.

Carre

no, M. L., Cardona, O. D., Barbat, A. H., (2007), Dis-

aster risk management performance index, Nat Haz-

ards 40 1-20.

Carre

no, M. L., Cardona, O. D., Barbat, A. H., (2012) New

methodology for urban seismic risk assessment from

a holistic perspective Bull Earthquake Eng, 10, 547-

565.

Mamdani, E. H., Assilian, S., (1975) An experiment in lin-

guistic synthesis with a fuzzy logic controller. Intern.

J. of Man-Machine Studies,7(1), 1-13.

Marulanda, M. C., Cardona, O. D., Barbat, A. H., (2009)

Robustness of the holistic seismic risk evaluation in

urban centers using the USRi, Nat Hazards, 49, 501-

516.

Kumpulainen, K., (2006) Vulnerability Concepts in Hazard

and Risk Assessment Geological Survey of Findand,

42, 65-74.

Saaty, T. L., Vargas, L. G., (1991) Prediction, projection,

and forecasting: applications of the analytical hier-

archy process in economics, ﬁnance, politics, games,

and sports, Kluwer Academic Publishers

AHolisticSeismicRiskSchemeUsingFuzzySets-PartOne:TheSocialSystemFragility

835