
Integrating Formal Verification and Simulation of Hybrid Systems
Rodin Multi-simulation Plug-in
Vitaly Savicks, Michael Butler and John Colley
School of Electronics and Computer Science, University of Southampton, Highfield, Southampton, U.K.
1 STAGE OF THE RESEARCH
Current work is at the third (final) year of the planned
research period. The first year consisted of the formu-
lation of the problem and the study of existing work in
order to discover possible solutions. It concluded with
a thorough literature review, an experimental evalua-
tion of the state of the art technologies, suitable for the
continuous-time (CT) aspect of our hybrid modelling
approach, and an outline of objectives with a research
path that linked the gathered knowledge together.
The second year has focused on the integration of
the tools, discovered in the first year, and the Rodin
platform for Event-B modelling. Based on the cho-
sen research path – integrating Event-B and CT aspect
via co-modelling and simulation – first, a widely used
standard for co-simulation has been selected. Further
work evolved around the study of the standard and co-
simulation principles, the definition of the simulation
semantics for both Event-B and CT models and the
implementation of a proof of concept using a trivial
hybrid system model.
The third year focuses on the technical aspects
and includes formalisation of the simulation algo-
rithm and its semantics, experimentation with alter-
native semantics, implementation of the actual co-
simulation tool called Rodin Multi-Simulation (RMS)
and its validation using a number of hybrid system ex-
amples from different domains.
2 OUTLINE OF OBJECTIVES
The foremost objective of this research is to develop a
solid framework that is capable of formal modelling,
verification and simulation of hybrid (also known as
cyber-physical) systems with respect to their discrete
and continuous aspects. Our attention is concentrated
on an open and extensible platform, suitable for both
academic research and industrial application, and a
simple, yet powerful formal language that fits well
with the task of safety-critical systems development
and supports essential features of abstraction, modu-
lar development and refinement, as well as facilitates
the difficult task of formal verification and validation.
The main goal is broken down into a number of
subgoals:
• To develop an open integrated solution for the for-
mal modelling, verification and co-simulation of
discrete-event (DE) models of controllers and the
interacting physical environment;
• To provide a generic simulation orchestration
mechanism called master that can simulate deter-
ministically an arbitrary number of interconnected
DE and CT subsystems;
• To produce an open and extensible co-simulation
tool, which is seamlessly integrated into an exist-
ing formal modelling framework, is efficient for
the simulation-based analysis of real-scale sys-
tems and is simple and easy to use;
• To conduct a comparison between the proposed
co-simulation approach and traditional simulation
techniques;
• To create a development pattern for hybrid sys-
tems based on the produced co-modelling and co-
simulation toolset.
3 RESEARCH PROBLEM
The heterogeneous nature of hybrid systems, which
consist of interleaving computational and physical do-
mains, often represented by a hierarchy of different
components, makes it difficult to use a single develop-
ment tool (Lee, 2008). It is also coming into practice
that an application of some formal method is required
for the rigorous analysis and assurance of the safety of
a developed system (Gnesi and Margaria, 2013). This
leads to an evident conclusion that a means of inte-
grating the existing domain-specific tools and tech-
nologies with the emphasis on formal methods is re-
quired (Marwedel, 2010). In this work we focus on
the idea of integrating formal modelling/verification
29
Savicks V., Butler M. and Colley J..
Integrating Formal Verification and Simulation of Hybrid Systems - Rodin Multi-simulation Plug-in.
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

with industrial-level simulation tools for different do-
mains, as we think this can negate or minimise the
limitations of the physical development in formal
methods and the absence of the rigorous analysis in
simulation tools.
4 STATE OF THE ART
The existing work and literature includes a number
of examples of the integration approaches. The most
notable are the co-simulation between Simulink and
clocked data flow in Signal (Tudoret et al., 2000),
the DESTECS project for modelling the DE aspect
of a hybrid system in VDM formal language and
CT aspect in the 20-sim physical modelling envi-
ronment (Fitzgerald et al., 2010), and the Ptolemy
project that focuses on the heterogeneous composi-
tion of components and different models of compu-
tation that define particular semantics (Brooks et al.,
2005). Although these technologies are very promis-
ing, they do not address the key problem of the
lack of integration between multiple development ap-
proaches and environments. To tackle this issue we
propose a generic integration solution, which is based
on a widely supported tool-independent standard for
model exchange and co-simulation called Functional
Mock-up Interface (Blochwitz et al., 2011), an open
physical modelling language Modelica (Fritzson and
Engelson, 1998) and a powerful and open toolset
Rodin (Abrial et al., 2010) for the rigorous analysis
of Event-B (Abrial, 2010).
4.1 Event-B
Event-B is a formal method for modelling and rig-
orous analysis of complex systems. The language
is inspired by Action Systems (Back, 1990) and B
Method (Abrial et al., 1991), and is based on the sim-
ple mathematical formalisms of set theory and first-
order logic. A system is modelled in Event-B as a
collection of state variables and guarded events that
act upon those variables, while the system properties
are modelled by invariants that must hold and can
be verified by deductive proof. The key feature that
distinguishes Event-B from other methods is the it-
erative modelling via proof-based refinement, which
lets a modeller introduce the details and increase
the complexity of the model in small steps (refine-
ments), whilst ensuring the correctness of the model
with respect to its specification through refinement
proofs. The other key feature is a powerful and ex-
tensible Rodin platform, which offers automatic proof
obligation generation and automatic/interactive prov-
ing capabilities, and, thanks to a collection of avail-
able plug-ins, provides additional automatic provers,
a mechanism for extending the existing language by
defining new theories (Butler and Maamria, 2013),
model checking (Leuschel and Butler, 2008), modular
development via decomposition (Silva et al., 2011),
UML modelling (Snook and Butler, 2008), code gen-
eration (Edmunds and Butler, 2011), etc.
A typical model in Event-B consists of a static
context, which defines the constants, sets and axioms,
and a dynamic machine, which contains the variables
and invariants that model system properties, and the
events that model the behaviour. An event may have a
number of input parameters, guards (event-enabling
predicates) and actions (variable modifiers), which all
happen at the same time (atomically) as the event gets
executed. If a number of events are enabled, execu-
tion is performed non-deterministically.
Besides the machines and context there may be the
following relations: a machine can see a context to be
able to use its definitions, a context can extend another
context with new static information, a machine can
refine another machine to introduce new data (vertical
refinement) or behaviour (horizontal refinement).
4.2 Modelica
Modelica is an open-source object-oriented language
for modelling and simulation of complex heteroge-
neous systems that may span a number of domains.
The language was designed to allow the tools to auto-
matically generate efficient simulation code with the
main objective to facilitate the exchange of models,
model libraries and simulation specifications.
Models in Modelica are mathematically described
by differential, algebraic and discrete equations with-
out the specification of causality (relationship be-
tween inputs and outputs). This enables high reusabil-
ity and readability of declarative (acausal) models, as
opposed to context-sensitive procedural approaches
where causality is fixed (e.g. Simulink). On the
other hand equation-based models are not oriented
to solution and therefore require more sophisticated
symbolic analysis capabilities from the tools. Never-
theless, Modelica is largely supported by the open-
source and commercial simulation tools, offers nu-
merous domain-specific libraries of reusable compo-
nents and continuously evolves as a language. Fol-
lowing is a list of the basic modelling constructs in
Modelica (Association et al., 2000):
• Basic data type components, such as Real, Integer,
Boolean and String;
• Structured components (classes), to enable hierar-
chical structuring;
SIMULTECH2014-DoctoralConsortium
30
• Component arrays, to handle real matrices, arrays
of submodels, etc.;
• Equations and/or algorithms (assignment state-
ments);
• Connections;
• Functions.
In the context of hybrid systems a particularly
interesting feature of the language is the capabil-
ity to model intermixed continuous and discrete dy-
namics. The discrete and sampled systems can be
modelled in Modelica using discrete state variables
(whose values are changing only at specific points
in time) and a when clause that activates equations
instantaneously on the event occurrence. A built-
in function sample(start,interval) can be used as a
condition of a when clause to trigger it when time =
start +n×interval,n ≥0, which is particularly useful
for modelling sampling. Some of these constructs are
demonstrated in a hybrid model of the classical exam-
ple of a bouncing ball that involves both the continu-
ous motion of the ball and discrete changes in velocity
at the bounce times:
model BouncingBall
parameter Real g=9.81;
parameter Real c=0.90; // elasticity constant
Real height(start=0); // height above ground
Real v(start=10); // velocity
equation
der(height) = v;
der(v) = -g; // derivative of v
when height<0 then // when bounce happens
reinit(v, -c*v); // reset v to -c*v
end when;
end BouncingBall;
4.3 Functional Mock-up Interface
Functional Mock-up Interface (FMI) is an open stan-
dard for tool-independent model exchange and co-
simulation. It provides a cross-platform API that
comes as a specification document, a set of C header
files to be implemented by an individual model and
a model description file schema for describing state
variables and capabilities of the model (Blochwitz
et al., 2012). The model code is built as a dy-
namic/shared library for the target platform and bun-
dled with the model description file into a Functional
Mock-up Unit (FMU) that can be used for modelling
and simulation in any FMI-compliant tool.
The aspect of the standard that describes Co-
Simulation is designed for coupling models and sim-
ulators in a co-simulation environment, where each
subsystem called Slave (an FMU representing either a
model or a coupled simulation tool) is solved by its in-
dividual solver. The simulation is coordinated by the
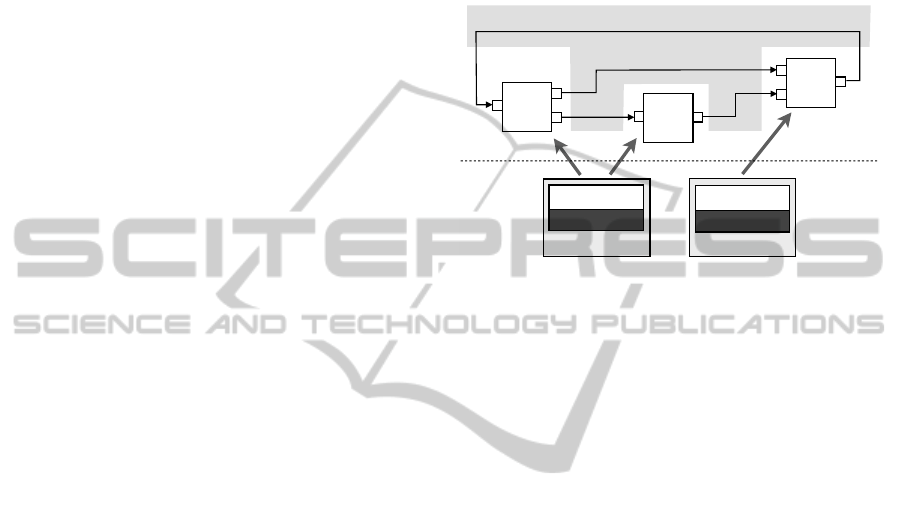
algorithm called Master (see Figure 1), which breaks
the simulation interval [t
start
,t
stop
] into discrete com-
munication steps tc
i
→tc
i+1
, at which it synchronises
Slaves and performs the data exchange. The standard
is designed to support a number of FMU capabilities
and a general class of simulation algorithms, although
it does not define the algorithm itself.
• Component arrays, to handle real matrices, arrays
of submodels, etc.;
• Equations and/or algorithms (assignment state-
ments);
• Connections;
• Functions.
In the context of hybrid systems a particularly
interesting feature of the language is the capabil-
ity to model intermixed continuous and discrete dy-
namics. The discrete and sampled systems can be
modelled in Modelica using discrete state variables
(whose values are changing only at specific points
in time) and a when clause that activates equations
instantaneously on the event occurrence. A built-
in function sample(start,interval) can be used as a
condition of a when clause to trigger it when time =
start +n⇥interval,n 0, which is particularly useful
for modelling sampling. Some of these constructs are
demonstrated in a hybrid model of the classical exam-
ple of a bouncing ball that involves both the continu-
ous motion of the ball and discrete changes in velocity
at the bounce times:
model BouncingBall
parameter Real g=9.81;
parameter Real c=0.90; // elasticity constant
Real height(start=0); // height above ground
Real v(start=10); // velocity
equation
der(height) = v;
der(v) = -g; // derivative of v
when height<0 then // when bounce happens
reinit(v, -c*v); // reset v to -c*v
end when;
end BouncingBall;
4.3 Functional Mock-up Interface
Functional Mock-up Interface (FMI) is an open stan-
dard for tool-independent model exchange and co-
simulation. It provides a cross-platform API that
comes as a specification document, a set of C header
files to be implemented by an individual model and
a model description file schema for describing state
variables and capabilities of the model (Blochwitz
et al., 2012). The model code is built as a dy-
namic/shared library for the target platform and bun-
dled with the model description file into a Functional
Mock-up Unit (FMU) that can be used for modelling
and simulation in any FMI-compliant tool.
The aspect of the standard that describes Co-
Simulation is designed for coupling models and sim-
ulators in a co-simulation environment, where each
subsystem called Slave (an FMU representing either a
model or a coupled simulation tool) is solved by its in-
dividual solver. The simulation is coordinated by the
algorithm called Master (see Figure 1), which breaks
the simulation interval [t
start
,t
stop
] into discrete com-
munication steps tc
i
!tc
i+1
, at which it synchronises
Slaves and performs the data exchange. The standard
is designed to support a number of FMU capabilities
and a general class of simulation algorithms, although
it does not define the algorithm itself.
time
gF
time + t0
FMU (DLL)
Subsystem A
Solver Tool A
Instances
Classes
master
A1
A2
B
Simulation Tool
Subsystem B
Solver
Figure 1: FMI master-slave architecture
5 METHODOLOGY
Our approach of integrating simulation into the Rodin
platform is comprised of several steps. First, we are
defining the semantics of a simulation step of both
discrete (Event-B models) and continuous (FMUs)
components, and derive a simulation API along with
a meta-model of the simulation composition graphs,
according to the FMI specification. Then, specifi-
cally for the Event-B components, we design a map-
ping from Event-B modelling constructs to our FMI-
compliant API. Next, we define our simulation master
algorithm. The final (current) stage consists of the im-
plementation of all developed ideas into a Rodin plug-
in and the following empirical validation on a number
of case studies.
5.1 Semantics
In our co-simulation approach, which is based on
the master-slave architecture of the FMI for Co-
Simulation v1.0 standard (MODELISAR, 2010), we
distinguish the simulation step of a DE component,
represented by an Event-B machine, and a CT com-
ponent that denotes an FMU.
The semantics of a continuous step (CStep) is de-
fined by the FMI standard and the underlying FMU’s
simulator, which is responsible for simulating the
model for a specified period of time.
The discrete step (DStep) is defined by a single
or a number of Event-B events, executed sequentially
Figure 1: FMI master-slave architecture.
5 METHODOLOGY
Our approach of integrating simulation into the Rodin
platform is comprised of several steps. First, we are
defining the semantics of a simulation step of both
discrete (Event-B models) and continuous (FMUs)
components, and derive a simulation API along with
a meta-model of the simulation composition graphs,
according to the FMI specification. Then, specifi-
cally for the Event-B components, we design a map-
ping from Event-B modelling constructs to our FMI-
compliant API. Next, we define our simulation master
algorithm. The final (current) stage consists of the im-
plementation of all developed ideas into a Rodin plug-
in and the following empirical validation on a number
of case studies.
5.1 Semantics
In our co-simulation approach, which is based on
the master-slave architecture of the FMI for Co-
Simulation v1.0 standard (MODELISAR, 2010), we
distinguish the simulation step of a DE component,
represented by an Event-B machine, and a CT com-
ponent that denotes an FMU.
The semantics of a continuous step (CStep) is de-
fined by the FMI standard and the underlying FMU’s
simulator, which is responsible for simulating the
model for a specified period of time.
The discrete step (DStep) is defined by a single
or a number of Event-B events, executed sequentially
IntegratingFormalVerificationandSimulationofHybridSystems-RodinMulti-simulationPlug-in
31

according to the language semantics. To avoid the ex-
plicit definition of the constituting sequence of events
we introduce the notion of a Wait event, which sig-
nifies the end of the step. Essentially, Wait must be
the only executable event(s) at synchronisation points,
whereas the sequence of events within a step can
be arbitrary and is defined by the individual model’s
logic. This offers a generic simulation solution and a
flexible model of refinement of the DE components.
The state of an individual component with respect
to simulation time can be defined as a function:
F : Time →V (1)
where V is the state of the component’s internal
variables. The evolution of each variable and its com-
ponent over time can be represented on a graph:
according to the language semantics. To avoid the ex-
plicit definition of the constituting sequence of events
we introduce the notion of a Wait event, which sig-
nifies the end of the step. Essentially, Wait must be
the only executable event(s) at synchronisation points,
whereas the sequence of events within a step can
be arbitrary and is defined by the individual model’s
logic. This offers a generic simulation solution and a
flexible model of refinement of the DE components.
The state of an individual component with respect
to simulation time can be defined as a function:
F : Time !V (1)
where V is the state of the component’s internal
variables. The evolution of each variable and its com-
ponent over time can be represented on a graph:
time
gF
time + t0
Figure 2: The state of a slave over time
where g is a state function defined over time in-
terval time...time + t. If t equals the communica-
tion step of the master, the simulation semantics of a
continuous component can be formally defined using
Event-B notation as follows:
machine C
variables F,time
event CStep =
any i,t,g
where
g 2[time...time+t] !V
g(time)=F(time)
P(g,i,F,time,t)
then
time := time +t
F := F [g
where parameter i is the component’s inputs and P
is the model properties, or properties that g must sat-
isfy. This formal model specifies the semantics of CT
components, as it depends on time and the continuous
function F. For the DE components we derive a sim-
pler definition that depends on the input and internal
variables:
machine D
var V, O
event DStep =
any i
where
i 2T
then
V,O := S(V,O,i)
where i is the input, O is the internal variables that
are also outputs, and S is a discrete state function.
Besides the notion of a Wait event we introduce
a similar concept of a Read event, which maps the
component’s inputs to Event-B input parameters and
enables the exchange of signals between DE and CT
components. Hence, Wait and Read events are the
only meta-constructs, required to provide the defined
co-simulation semantics.
5.2 Event-B Mapping
A representative mapping of an Event-B machine that
models a water tank controller (controls the water
level in a leaking tank by switching the input valve)
to a discrete simulation component is demonstrated
below.
machine tankController0
variables valve
events
SwitchOn ˆ= any l where l < LT
then valve := on end
NoSwitch ˆ= any l where l LT ^l HT
then skip end
SwitchOff ˆ= any l where l > HT
then valve := off end
end
All three events of this abstract machine would
map to Read events and Wait events, thus simulation
will progress by executing one of the events, depend-
ing on the value of l, which is an input signal of the
sensed water level from the environment.
The model can be easily refined whilst keep-
ing simulation semantics consistent with the abstract
model. As new events are introduced, the Read and
Wait events become distinct:
machine tankController1 refines tankController0
variables valve,level,state
events
ReadLevel ˆ= any l where state = 0
then level := l end
DecideOn ˆ= where state = 1 ^level < LT
then state := 2 end
DecideSkip ˆ= where state = 1^level LT ^level HT
then state := 3 end
DecideOff ˆ= where state = 1^level > HT
then state := 4 end
SwitchOn refines SwitchOn ˆ= witness l = level
where state = 2 then valve := on end
Figure 2: The state of a slave over time.
where g is a state function defined over time in-
terval time.. .time + t. If t equals the communica-
tion step of the master, the simulation semantics of a
continuous component can be formally defined using
Event-B notation as follows:
machine C
variables F,time
event CStep =
any i,t,g
where
g ∈[time.. .time+t] →V
g(time) = F(time)
P(g,i,F,time,t)
then
time := time + t
F := F ∪g
where parameter i is the component’s inputs and P
is the model properties, or properties that g must sat-
isfy. This formal model specifies the semantics of CT
components, as it depends on time and the continuous
function F. For the DE components we derive a sim-
pler definition that depends on the input and internal
variables:
machine D
var V, O
event DStep =
any i
where
i ∈T
then
V,O := S(V,O,i)
where i is the input, O is the internal variables that
are also outputs, and S is a discrete state function.
Besides the notion of a Wait event we introduce
a similar concept of a Read event, which maps the
component’s inputs to Event-B input parameters and
enables the exchange of signals between DE and CT
components. Hence, Wait and Read events are the
only meta-constructs, required to provide the defined
co-simulation semantics.
5.2 Event-B Mapping
A representative mapping of an Event-B machine that
models a water tank controller (controls the water
level in a leaking tank by switching the input valve)
to a discrete simulation component is demonstrated
below.
machine tankController0
variables valve
events
SwitchOn ˆ= any l where l < LT
then valve := on end
NoSwitch ˆ= any l where l ≥ LT ∧l ≤ HT
then skip end
SwitchOff ˆ= any l where l > HT
then valve := off end
end
All three events of this abstract machine would
map to Read events and Wait events, thus simulation
will progress by executing one of the events, depend-
ing on the value of l, which is an input signal of the
sensed water level from the environment.
The model can be easily refined whilst keep-
ing simulation semantics consistent with the abstract
model. As new events are introduced, the Read and
Wait events become distinct:
machine tankController1 refines tankController0
variables valve,level,state
events
ReadLevel ˆ= any l where state = 0
then level := l end
DecideOn ˆ= where state = 1∧level < LT
then state := 2 end
DecideSkip ˆ= where state = 1∧level ≥LT ∧level ≤HT
then state := 3 end
DecideOff ˆ= where state = 1∧level > HT
then state := 4 end
SwitchOn refines SwitchOn ˆ= witness l = level
where state = 2 then valve := on end
SIMULTECH2014-DoctoralConsortium
32

NoSwitch refines NoSwitch ˆ= witness l = level
where state = 3 then skip end
SwitchOff refines SwitchOff ˆ=witness l = level
where state = 4 then valve := off end
end
In the refinement the ReadLevel becomes a Read
event and SwitchOn, NoSwitch and SwitchOff – Wait
events. The flexibility of marking same/multiple
events as Read or Wait events enables simulation of
control behaviour alongside its refinement and veri-
fication, ensuring that developed models are correct
by construction and interact with the environment as
expected.
5.3 Master Algorithm
Our master is a fixed step size generic algorithm,
based on a two-list simulation approach from the
VHDL (Mazor and Langstraat, 1993) and designed to
comply with the FMI standard, i.e. developed to re-
flect the recommended use of the FMI API. It divides
the simulation into discrete steps and communicates
the data between components at the step boundaries.
At each simulation cycle an update list is checked for
components that need to be evaluated according to
their step size and progression in time. If a component
is found in the update list, it is put into an evaluation
list. All evaluated components then exchange the data
and advance their simulation state. The outline of the
algorithm (with API calls) is as follows:
1. Instantiate all components:
Component.instantiate())
2. Initialise all components:
Component.initialise(startTime,
stopTime)
3. Set the simulation time to a start time, put all com-
ponents into the update list (“time zero initialisa-
tion”) and begin the simulation loop.
4. Check the update list for the components to be
evaluated at the current simulation time and put
them into the evaluation list.
5. For each component in the evaluation list, write
all outputs:
Component.writeOutputs())
6. Read all inputs:
Component.readInputs())
7. Perform the step:
Component.doStep(time, stepSize))
8. Put evaluated components back to the update list
increasing the next evaluation time by the corre-
sponding step size.
9. If the time has reached the stop time then stop,
otherwise progress the time and go back to step 4.
10. Terminate components:
Component.terminate())
The step size is defined for each component indi-
vidually at the master level, hence Event-B models do
not have to be timed. In addition, the master uses our
generic API and therefore does not rely on a particu-
lar implementation of the individual component type,
making it possible to extend co-simulation capabili-
ties by introducing other types of components without
the need to modify the algorithm.
5.4 Co-simulation Environment
Our simulation environment RMS (Rodin Multi-
Simulation) is currently being developed. It already
implements the described master algorithm and an
extensible component meta-model that supports both
Event-B and FMI components. The environment en-
ables import, configuration and diagrammatic com-
position of components via input/output ports, con-
trolled simulation and real-time visualisation of the
signals, simulation trace recording/playback, dead-
lock and invariant checking via ProB tool (Leuschel
and Butler, 2008). The preliminary work and experi-
ments are explained in more detail in (Savicks et al.,
2014).
6 EXPECTED OUTCOME
The goal of this work is to provide a development so-
lution, targeted at hybrid systems, that combines for-
mal modelling, verification and physical simulation,
in order to ensure the safety and reliability of con-
structed systems. We expect to implement and offer
modellers a tool that enables both the rigorous anal-
ysis (using Event-B) of the discrete aspect of hybrid
systems and the simulation-based analysis of the in-
teraction with the physical environment. We hope
that by integrating simulation and formal verification
technologies system engineers will benefit in terms of
clearer understanding of the intricate interactions be-
tween the discrete and continuous aspects of a hybrid
system, be able to formally verify its safety and reli-
ability properties and to analyse its behaviour in a re-
alistic model of environment. This should ultimately
reduce the cost and time of the development and im-
prove the quality of implemented embedded software.
IntegratingFormalVerificationandSimulationofHybridSystems-RodinMulti-simulationPlug-in
33

ACKNOWLEDGEMENT
This work is part of the ADVANCE Project (Ad-
vanced Design and Verification Environment for
Cyber-physical System Engineering) funded by the
European Commission (http://www.advance-ict.eu).
REFERENCES
Abrial, J. (2010). Modeling in Event-B: system and software
engineering. Cambridge University Press.
Abrial, J., Butler, M., Hallerstede, S., Hoang, T., Mehta, F.,
and Voisin, L. (2010). Rodin: an open toolset for mod-
elling and reasoning in Event-B. International Jour-
nal on Software Tools for Technology Transfer (STTT),
12(6):447–466.
Abrial, J., Lee, M., Neilson, D., Scharbach, P., and
Sørensen, I. (1991). The B-method. In VDM’91 For-
mal Software Development Methods, pages 398–405.
Springer.
Association, M. et al. (2000). Modelica–a uni-
fied object-oriented language for physical sys-
tems modeling: Tutorial version 1.4. [Online]
http://www.modelica.org/publications.
Back, R.-J. (1990). Refinement calculus, part II: Paral-
lel and reactive programs. In Stepwise Refinement
of Distributed Systems Models, Formalisms, Correct-
ness, pages 67–93. Springer.
Blochwitz, T., Otter, M., Akesson, J., Arnold, M., Clauss,
C., Elmqvist, H., Friedrich, M., Junghanns, A.,
Mauss, J., Neumerkel, D., et al. (2012). Functional
mockup interface 2.0: The standard for tool indepen-
dent exchange of simulation models. In 9th Interna-
tional Modelica Conference, Munich.
Blochwitz, T., Otter, M., Arnold, M., Bausch, C., Clauß, C.,
Elmqvist, H., Junghanns, A., Mauss, J., Monteiro, M.,
Neidhold, T., et al. (2011). The Functional Mockup
Interface for tool independent exchange of simulation
models. In Modelica’2011 Conference, March, pages
20–22.
Brooks, C., Lee, E. A., Liu, X., Zhao, Y., Zheng, H., Bhat-
tacharyya, S. S., Cheong, E., Goel, M., Kienhuis, B.,
Liu, J., et al. (2005). Ptolemy II: Heterogeneous con-
current modeling and design in Java.
Butler, M. and Maamria, I. (2013). Practical theory exten-
sion in event-b. In Theories of Programming and For-
mal Methods, pages 67–81. Springer.
Edmunds, A. and Butler, M. (2011). Tasking Event-B: An
extension to Event-B for generating concurrent code.
Fitzgerald, J., Larsen, P., Pierce, K., Verhoef, M., and Wolff,
S. (2010). Collaborative modelling and co-simulation
in the development of dependable embedded systems.
In Integrated Formal Methods, pages 12–26. Springer.
Fritzson, P. and Engelson, V. (1998). Modelica — a uni-
fied object-oriented language for system modeling
and simulation. In ECOOP’98—Object-Oriented Pro-
gramming, pages 67–90. Springer.
Gnesi, S. and Margaria, T. (2013). Formal Methods for In-
dustrial Critical Systems. Wiley Online Library.
Lee, E. A. (2008). Cyber physical systems: De-
sign challenges. In International Symposium on
Object/Component/Service-Oriented Real-Time Dis-
tributed Computing (ISORC). Invited Paper.
Leuschel, M. and Butler, M. (2008). ProB: an auto-
mated analysis toolset for the B method. International
Journal on Software Tools for Technology Transfer,
10(2):185–203.
Marwedel, P. (2010). Embedded and cyber-physical sys-
tems in a nutshell.
Mazor, S. and Langstraat, P. (1993). A Guide to VHDL.
Springer US.
MODELISAR (2010). Functional Mock-up Interface for
Co-Simulation, Version 1.0.
Savicks, V., Butler, M., and Colley, J. (2014). Co-simulating
Event-B and continuous models via FMI.
Silva, R., Pascal, C., Hoang, T. S., and Butler, M. (2011).
Decomposition tool for event-b. Software: Practice
and Experience, 41(2):199–208.
Snook, C. and Butler, M. (2008). UML-B and Event-B: an
integration of languages and tools.
Tudoret, S., Nadjm-Tehrani, S., Benveniste, A., and
Str
¨
omberg, J. (2000). Co-simulation of hybrid sys-
tems: Signal-Simulink. In Formal Techniques in
Real-Time and Fault-Tolerant Systems, pages 623–
639. Springer.
SIMULTECH2014-DoctoralConsortium
34
