
Coherence Net
A New Model of Generative Cognition
Michael O. Vertolli and Jim Davies
Institute of Cognitive Science, Carleton University, 1125 Colonel By Dr., Ottawa, Canada
Keywords: Generative Cognition, Machine Learning, Multi-Label, Bag-of-Words, Evolutionary Algorithms.
Abstract: We propose a new algorithm and formal description of generative cognition in terms of the multi-label bag-
of-words paradigm. The algorithm, Coherence Net, takes its inspiration from evolutionary strategies,
genetic programming, and neural networks. We approach generative cognition in spatial reasoning as the
decompression of images that were compressed into lossy feature sets, namely, conditional probabilities of
labels. We show that the globally parallel and locally serial optimization technique described by Coherence
Net is better at accurately generating contextually coherent subsections of the original compressed images
than a competitive, purely serial model from the literature: Coherencer.
1 INTRODUCTION
Generative cognition has been implicated in a broad
range of cognitive faculties, including but not
limited to imagination, episodic memory, and spatial
navigation (Vertolli & Davies, 2013; 2014). By
generative cognition, we mean the production of
new output from a given data set that is not
explicitly stored in the data set. As a cognitively
salient example, the hippocampus’s ability to
anticipate new objects and spatial relations from
those that are remembered would fall under the class
of generative cognition (Mullally & Maguire, 2013).
When an individual imagines a new scene on the
basis of an environmental trigger with elements that
were not explicitly encoded in memory, this would
also qualify. It can be viewed as a form of
decompression where data lost in the compression
phase is deduced from implicit relations present in
the compressed data. It is also distinct from
creativity in that the result can be mundane.
We chose to approach this problem using a
multi-label, bag-of-words approach (for review of
the multi-label literature, see Zhang & Zhou, 2013).
In place of documents and words, we modeled a
visual task using images and their associated pixels.
Each image has labels associated with pixel clusters
that indicate objects in the image. Since a given
image can have many objects, each image is given a
collection of labels instead of one, hence multi-label.
Unlike the standard bag-of-words approach, we
are not interested in the labeling process. We assume
images and their corresponding pixel clusters have
been correctly labeled. We derive the images and
associated labels from the Peekaboom database of
labeled images (Von Ahn, Liu, & Blum, 2006). This
database is one of the most extensive in the
literature, with over 50,000 manually labeled
images. Instead of the standard classification or
labeling task, we are interested in using associations
between the labels to select a collection that could be
used to generate a plausible new image instance.
According to Zhang and Zhou’s (2013) formal
description of the multi-label task, generative
cognition and classifier tasks are the inverse of one
another.
2 FORMAL DEFINITION
Zhang and Zhou (2013) describe the multi-label task
in the following way. Let denote the input space
(e.g., images, documents) and denote the label
space of all possible labels. The standard task is to
learn a function
⋅
that takes as input some
member
from the input space and returns some
combination of labels from the label space as output
(i.e., ∶→2
). We learn this function from the
multi-label training set, where all training
examples are described in terms of their input
features and corresponding label sets (i.e.,
,
|
1
). Note that
is a
308
Vertolli M. and Davies J..
Coherence Net - A New Model of Generative Cognition.
DOI: 10.5220/0005149203080313
In Proceedings of the International Conference on Evolutionary Computation Theory and Applications (ECTA-2014), pages 308-313
ISBN: 978-989-758-052-9
Copyright
c
2014 SCITEPRESS (Science and Technology Publications, Lda.)

d-dimensional feature vector
,
,…,
, where
each feature corresponds to a single dimension in the
input space. In the standard classification task we
want to find the function
⋅
, called the classifier,
in order to predict the correct labels that go with an
as yet unseen input .
By contrast, the generative cognition task is to
find a function
⋅
that is the inverse of
⋅
(i.e.,
∶2
→). This means that it takes as input a label
or set of labels and outputs one of the original input
instances (e.g., image, document). We propose to
preliminarily achieve this through the parallel task of
finding a set of labels
(
∶2
→2
)—where
indexes the current iteration of the algorithm—that
extend the input and together indicate some
instance
. We can think of the generation task as
finding a function
⋅
, called the generator, that
finds a subset of labels that would be picked by an
accurate classifier
⋅
for some instance
in the
input space . Formally, this means
∃
.
⊇
(1)
We can take the manual labeling of the Peekaboom
database as another function (
∶2
→) that
maps a set of labels
to the subsets of features that
indicated them (e.g., for the label ‘dog,’ a given
collection of pixels that look like a dog). Thus, the
composition of
and
meets the requirements of
the given task (i.e.,
∘
).
Models of both the generative and classifier tasks
return a real-valued function
⋅,⋅
that takes an
instance-label pair , as input and outputs a
number denoting the confidence that the label is
accurate for that instance (i.e., ∶→).
However, in the generative case, we assess the
confidence of a label relative to the current
potential set of labels
. If we think of
as a
hypothetical instance , then we get a modified
version of
⋅,⋅
’s input, or
≅
,
, for the
model of the generator. For both the generator and
the classifier tasks,
⋅,⋅
should output a larger
confidence value on a relevant label ′ than an
irrelevant label ′′ for a given instance or
hypothetical instance , or
,′
,′′
(Zhang and Zhou, 2013). The multi-label classifier
⋅
and generator
⋅
can then be derived from
⋅,⋅
by incorporating a thresholding function that
determines how large the confidence needs to be for
a label to be considered accurate for a given instance
(i.e., ∶→). We then get the output,
or
, by assessing for a given instance or
hypothetical instance whether each possible label
passes the threshold given by
. Formally, this
means
|
,
,∈
(2)
|
,
,∈
(3)
In effect, both functions use
⋅
to dichotomize Y
into relevant and irrelevant label sets (Zhang and
Zhou, 2013). However, the generative
⋅
is slightly
more complex as the hypothetical ≅
changes
with each iteration of the algorithm.
Though standard machine learning techniques
can accurately resolve the standard multi-label
problem, the generative problem suggests a different
approach. At minimum, since there are often many
possible
that might satisfy equation 1 and we are
not interested in one
over any other, many of the
standard techniques are more thorough than is really
required by the task. Thus, the fact that ∼
should not necessarily suggest that simply reversing
the directionality of one of the standard techniques is
a good solution; though, some researchers have
effectively taken this approach in similar domains
(see, for example, Hinton, Osindero, & Teh, 2006).
Vertolli and Davies (2013; 2014), by contrast,
showed that generative cognition is amenable to
heuristic optimization techniques and, thus, we turn
to this approach in order to address this task.
We will describe a new, more cognitively
plausible heuristic optimization algorithm called
Coherence Net. We will then test how this algorithm
performs against a competitive, serial, local hill
searching algorithm called Coherencer that has been
shown to be competitive in the literature (Vertolli &
Davies, 2013; 2014).
3 TASK DESCRIPTION
In Vertolli and Davies (2013; 2014), the task is to
imagine a fleshed-out scene from a single word
query. The model is given a query label (e.g., “car”)
with which to generate a collection of other labels
(e.g., “road” and “sky”). This collection needs to be
semantically coherent: the retrieved labels must
belong together. For example, a scene containing
“bow,” “violin,” and “arrow” would be incoherent
because it mixes two senses of the meaning “bow.”
Supported by cognitive limitations in working
memory, Vertolli and Davies restrict these
collections to 5 labels, including the query. We
continue in this tradition as it provides a simpler,
preliminary evaluation than dealing with larger label
sets or sets of mixed sizes.
The algorithms select the four other labels by
their conditional probability ∶→, which
they approximate from the conditional relative
CoherenceNet-ANewModelofGenerativeCognition
309

frequency of pairs of labels. Mainly, for labels
and, the conditional relative frequency is the total
number of image instances that contain both labels
(
,
∈
|
,∈
) divided by the total
number of image instances that contain the given
label (
,
∈
|
∈
). Formally, this
means
|
≅||||
⁄
(4)
One important property of this formalization is that
it is non-commutative (i.e., P yields a different value
for a-b than it does for b-a). Parallel research on co-
occurrence in the machine learning literature
suggests that this is more realistic and that most
models do not account for it (see Huang, Yu &
Zhou, 2012; Zhang & Zhou, 2013).
We describe the cognitive generation task as a
decompression step in a compression-decompression
sequence (see Vertolli, Kelly, & Davies, 2014), with
the classification task as the related compression
task. That is, we assume that, after the initial
processing required to derive the labels , the
original instances are no longer explicitly
accessible. They have been reduced to the triples
,,
|
,∈, in the memory
of the agent or model. Thus, the condition from
equation 1, with the modifier that
|
|
5, is not
trivial:
⋅
must, from a single input label, output a
potential instance on the basis of
⋅,⋅
,
⋅
, and .
In summary, the current task requires the
generative decompression of conditional
probabilities into a contextually coherent, 5-label
combination on the basis of a query label that is
included in the set. The context is accurately
reproduced if at least one of the original images
contains the same 5-label combination produced by
the agent. If none of the original images contain the
label combination, we assume the context is not
coherent.
We hypothesize that our software agent, called
Coherence Net, will outperform Coherencer (a
competing software agent, described below) by
capturing the best of both serial and parallel
functionality described in Vertolli and Davies (2013;
2014) and Thagard (2000). Coherence Net
effectively explores a larger portion of the search
space with a decreased chance of getting stuck on
local optima by capitalizing on a global, parallel
architecture with local serial transitions.
4 IMPLEMENTATION
We proceed by giving a formal outline of
Coherencer following Vertolli and Davies (2013;
2014) and a description of Coherence Net.
Coherencer is the visual coherence subsystem of
the SOILIE imagination architecture (Breault,
Ouellet, Somers, & Davies, 2013; Vertolli, Breault,
Ouellet, Somers, Gagné, & Davies, 2014). In this
modality, it is tasked with generating contextually
coherent label sets corresponding to a single word
input. Coherencer is a serial algorithm that
implements a heuristic local hill search.
Coherencer
,
1. Initialize , , ,
2. For 1 to
|
|
|
| do
3. Set
,
4.
5. If
∑
∈
do
6.
0
7. Else
8.
min
,
,∀∈
9. For ∈
do
10. If
,
do
11.
∪
12. If
|
|
5 do
13. Return
∪
14. Else
15. ∪
16.
17. If
|
|
0 do
18.
∪rand
19. 1
20. Else
21. Return
′
∪
Figure 1: Pseudocode for Coherencer.
Coherencer’s algorithm proceeds as follows (see
Figure 1 for pseudocode). First, the label set
of
the initial hypothetical instance
in
⋅,⋅
is
defined as the top-4 labels with the highest
conditional probability with the query () or
|∀∈.
|
|
|,1
4. The function
⋅,⋅
acts on the subset of
, called
, that contains the elements in the
current
and their corresponding conditional
probabilities (i.e.,
,,
|
∈
,∈
∪
). Specifically,
the function
⋅,⋅
sums over the conditional
probabilities of the subset of triples in
that
contain ,
,,
|
∈
∨
, or
,
∑
∈
(5)
The function
⋅
evaluates the current total context
and, if it passes a threshold
, outputs 0
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
310

allowing the algorithm to return
∪ as a valid
set of labels for the generated instance
.
Otherwise, it outputs the minimum
⋅,⋅
value in
, effectively discarding the associated label. We
can express this formally as
0, if
∑
∈
(6)
argmin
,
,∀∈
,
if
∑
∈
(7)
where argmin returns the lowest
⋅,⋅
value.
Since
|
|
5 is a condition for the
termination of the search, a new label ′ is randomly
selected from , where
|
|
0
,
|
,
,1
|
|
|
|
.
If at any point ||0, the result will be
′
∈
argmax
∈
,
1
|
|
|
|
(8)
where argmax′
⋅
selects the index with the highest
corresponding value.
Coherence Net is a hybrid of a number of
features from evolutionary strategies, genetic
programming, and neural networks. It was inspired
by an attempt to give an artificial neural network
representation to the standard evolutionary algorithm
approach, which was originally inspired by DNA
replication in a population of chromosomes
(Holland, 1975).
Coherence Net represents the standard
chromosomal abstraction of evolutionary algorithms
as a five-tiered tree of nodes similar to the derivation
trees used in grammar guided genetic programming
(GGGP; for review, see McKay, Hoai, Whigham,
Shan, & O’Neill, 2010). Each tier (
) for
15 contains an ordered list of nodes. Each
node contains a set of integers of cardinality 1, , 2,
2, and 5, for each respective tier. The integers are all
in base-10 except for the first tier, which is in base-
2, and they index nodes of the next lowest tier
(
). The parameter is the minimum number of
bits needed to create an ordered list with the
elements of randomized, or
. Extra indices
for a given are re-indexed modulus ||. For
example, 12 encodes 4096 options but only
2974 are needed; if a number, z, is greater than 2973,
we take z modulus 2974 instead.
Functionally, Coherence Net can be thought of as
a parallelized version of Coherencer (see Figure 2
for pseudocode). In place of
, we have a collection
of instances of of
,
∗
,
,…,
for
1|
| that is represented by the nodes of
.
All the elements of
∗
are randomly initialized from
with the possibility of repetition.
∗
and
∗
are
defined similarly with reference to . The functions
∗
⋅,⋅
and
∗
⋅
differ by acting on
⊂
∗
: a
random, 5 member subset of
∗
that indicates a
generalized hypothetical instance. Each
is
represented by a node at
. The resulting function is
∗
,
∈
|
∈
|
0
|
(9)
Note that the set added to the sum in
∗
⋅,⋅
, by
acting on while the sum acts on [0,1), places
greater emphasis on all pairs of labels co-occurring
at least once (i.e.,
|
0) than the conditional
probability sums. This is the first major difference
from Coherencer. The function
∗
∗
indicates a
constant threshold () that determines acceptance of
the entire set and termination of the search (like
Coherencer’s ). If the threshold is not passed, then
∗
argmax
∗
,
,
∀
∈
(10)
where is an infinitesimal. This function effectively
filters the subset
to its maximum member in a
variation of five member tournament selection (for
the genetic algorithm equivalent, see Miller &
Goldberg, 1995). If at any point the filtration results
in the the number of unique tier-4 nodes being less
than forty percent of , or
|
|
∀∈
|
0.4,
a destabilization step repopulates
such that
|
|
∀∈
|
.
CoherenceNet
∗
,
1. Initialize ,
∗
,
∗
2. For 1 to
∗
do
3. Set
∗
4. For 1 to |
| do
5. If
∗
,
∗
∗
do
6. Return
∪
7.
∗
8. While |
∗
||
∗
| do
9. Set
10. If
∗
,
∗
do
11.
←
22. If
|
|
∀∈
|
0.4|
∗
| do
23.
←
|
∀∈
24. While
|
|
∀∈
|
|
∗
| do
25.
′←rand
|
|
|
|
26. For ∈
do
27. If
∗∗
1/|
| do
28. 1mod2
29. 1
30. Return
′
∗
Figure 2: Pseudocode for Coherence Net.
CoherenceNet-ANewModelofGenerativeCognition
311
In order to search in parallel across the entire
collection of
’s, we abandoned the sequential
search in favor of a purely stochastic ‘noise’ step.
The noise step causes stochastic fluctuations in the
elements of that are being instantiated in
∗
over
the course of . Since can never be exhausted in
this format, we define a new iteration cap
∗
50
for . As with Coherencer, we define a variation of
⋅
′
∗
∈
argmax
∗∗
,
,
1
∗
∪
(11)
We then define two new functions,
∗∗
⋅,⋅
and
∗∗
⋅
, in order to account for the noise step.
The function
∗∗
⋅,⋅
is defined on the local
context (
) and computes the current probability
that the label ∈
will change from fluctuations
at
using the inclusion-exclusion principle.
Formally this can be described by
∗∗
,
⋃
∑
∑
∩
∑
∩
∩
⋯
1
⋂
(12)
where is the cardinality of sets in
and
1/|
|,∀ is defined as the probability of a bit
changing in the noise step. Since the probability of
each bit changing is independent and, thus, the
probability of multiple bits changing is the product
of the constant
, equation 10 can be simplified to
∗∗
,
∑
1
1/|
|
(13)
(see Brualdi, 2010). The function
∗∗
rand0,1 acts as the pseudo-random number
generator for the stochastic function
∗∗
⋅,⋅
. Since
the noise step can result in
∉, mainly
,,
|
,∈,, we expand to
∗
∪
,,100
|
,∈,
in order
to avoid these invalid sets.
5 METHOD
There are two models that were compared:
Coherencer and Coherence Net. The entire
Peekaboom database was filtered to remove all
images with fewer than five labels and any labels
that only occurred in those images. A total of 8,372
labels and 23,115 images remained after filtration.
The images were compressed to and
∗
.
Each of the 8,372 labels was processed by both
models 5 times per threshold. Each query plus four
returned labels are the elements of a new,
hypothetical image instance. The results for each of
the algorithms were assessed with regard to the
original images. If at least one of these images
contained the five labels that were selected by a
particular algorithm, including the query, the
algorithm scored one point. If there were no images
containing the five labels, they did not score a point.
The results were averaged for each threshold.
6 RESULTS
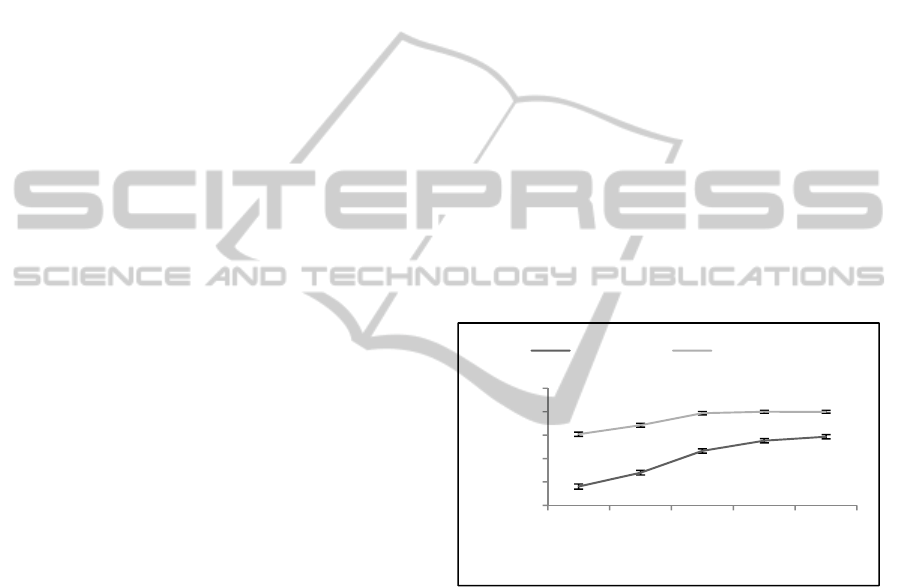
The results are reported in Figure 3 for each of the
models across half of the parameter space, which
ranges from 0 to 1. Both models level off after a
threshold of 0.5. The adjusted Wald confidence
interval for binomial (success or fail) proportions
was used (see Reiczigel, 2003). The max average
percent correct for Coherence Net is 90.0 (n =
7533.6) and for Coherencer is 79.3 (n = 6639.8).
Pearson chi-square test demonstrates that the
difference in the max number correct was
statistically significant, χ
2
(1, N=16744) = 363.63,
p <.000, φ = 0.15.
Figure 3: Percent correct for each model across the
threshold parameter space.
7 DISCUSSION
The results support the notion that Coherence Net
outperforms Coherencer at generating hypothetical
image label sets. It provides one of the first machine
learning techniques designed for generative
cognition. This, in turn, lends greater support to both
the related theories described by Vertolli and Davies
(2013; 2014) and Thagard (2000).
Thagard (2000) proposed both serial
optimization techniques and parallel or connectionist
techniques as valid approaches for dealing with
contextual coherence. Thagard argues that the
parallel structure better approaches the global
50
60
70
80
90
100
0,1 0,2 0,3 0,4 0,5
PercentCorrect
ThresholdValue
Coherencer CoherenceNet
ECTA2014-InternationalConferenceonEvolutionaryComputationTheoryandApplications
312

optimum by avoiding local optima. However, before
concluding his discussion, Thagard states explicitly
that serial algorithms are important for
understanding bounded rationality in humans.
Vertolli and Davies (2014) have shown that
functionally serial processing techniques can be
better than parallel algorithms when the feature set is
low level (e.g., conditional probabilities), low
dimensionality (e.g., only one feature), and high
combinatoric load. However, they leave open the
possibility that some combination of parallel and
serial techniques could explain how bounded
rationality approaches optimal functionality.
The current work supports and extends these
authors by implementing a parallelized serial
processing system with similarities with
connectionist approaches in its artificial neural
network representation: Coherence Net. As Thagard
predicted, greater parallelization increased the
optimality of the system as a whole. We have also
extended their work by providing a formal
description of the task and algorithms.
It is worth noting that, outside of the quantitative
testing metric, it is challenging to interpret the literal
output of each of the models. At times, it is clear
why Coherence Net outperformed Coherencer. For
example, given the query ‘robber,’ Coherence Net
returned ‘steal,’ ‘thief,’ ‘mask,’ and ‘jail’ while
Coherencer returned ‘steal,’ ‘thief,’ ‘money,’ and
‘square.’ Coherence Net’s result occurs in an image
and Coherencer’s does not. However, for the query
‘bank,’ Coherence Net returned ‘fruit,’ ‘away,’
‘keeps,’ and ‘an’ while Coherencer returned ‘hand,’
‘atm,’ ‘credit,’ and ‘keeps.’ Though Coherence
Net’s output does occur in an image and
Coherencer’s does not, it is not obvious which result
is actually more desirable as a model of imagination.
Another caveat is that many of the parameters
used, especially the number the nodes at each tier,
are arbitrary. Generally, more nodes improved the
search space but increased the search time. We used
1000 nodes for tiers 1 through 3 and 2500 nodes for
tiers 4 and 5 as we found these numbers worked well
in a reasonable amount of time. Future work will
evaluate many of these properties in greater detail.
REFERENCES
Breault, V., Ouellet, S., Somers, S., & Davies, J. (2013).
SOILIE: A computational model of 2D visual
imagination. In R. West & T. Stewart (eds.),
Proceedings of the 12th International Conference on
Cognitive Modeling, Ottawa, ON.
Brualdi, R. A. (2010). Introductory Combinatorics, Fifth
Edition. Pearson Education, Inc.
Hinton, G. E., Osindero, S., & Teh, Y. W. (2006). A fast
learning algorithm for deep belief nets. Neural
computation, 18(7), 1527-1554.
Holland, J. H. (1975), Adaptation in Natural and Artificial
Systems, University of Michigan Press, Ann Arbor.
Huang, S. J., Yu, Y., & Zhou, Z. H. (2012).Multi-label
hypothesis reuse. In Proceedings of the 18th ACM
SIGKDD international conference on Knowledge
discovery and data mining (pp. 525-533).ACM.
Maguire, E. A., & Mullally, S. L. (2013). The
hippocampus: A manifesto for change. Journal of
Experimental Psychology: General, 142(4), 1180.
Mckay, R. I., Hoai, N. X., Whigham, P. A., Shan, Y., &
O’Neill, M. (2010). Grammar-based genetic
programming: a survey. Genetic Programming and
Evolvable Machines, 11(3-4), 365-396.
Miller, B. L., & Goldberg, D. E. (1995).Genetic
Algorithms, Tournament Selection, and the Effects of
Noise. Urbana, 51, 61801.
Reiczigel, J. (2003). Confidence intervals for the binomial
parameter: some new considerations. Statistics in
Medicine, 22(4), 611-621.
Thagard, P. (2000). Coherence in thought and action.
Cambridge, MIT Press.
Vertolli, M. O., Breault, V., Ouellet, S., Somers, S.,
Gagné, J. & Davies, J. (2014). Theoretical assessment
of the SOILIE model of the human imagination,
Proceedings of the 36th Annual Conference of the
Cognitive Science Society. Quebec City, QC.
Vertolli, M. O. & Davies, J. (2013).Visual imagination in
context: Retrieving a coherent set of labels with
Coherencer. In R. West & T. Stewart (eds.),
Proceedings of the 12
th
International Conference on
Cognitive Modeling, Ottawa, ON.
Vertolli, M. O. & Davies, J. (2014). Coherence in the
visual imagination: Local hill search outperforms
Thagard’s connectionist model, Proceedings of the
36th Annual Conference of the Cognitive Science
Society. Quebec City, QC.
Vertolli, M. O., Kelly, M. A., & Davies, J. (2014).
Perception and generation as a compression-
decompression dyad, Proceedings of the 7th
Conference on Artificial General Intelligence (AGI),
Quebec City, QC: AGI.
Von Ahn, L., Liu, R., &Blum, M. (2006). Peekaboom: a
game for locating objects in images. In Proceedings of
the SIGCHI Conference on Human Factors in
Computing Systems (pp. 55-64).ACM.
Zhang, M. & Zhou, Z. (2013).A review on multi-label
learning algorithms. IEEE Transactions on Knowledge
and Data Engineering, PP(99), 1-59.
CoherenceNet-ANewModelofGenerativeCognition
313
