Emergent Induction of L-system Grammar
from a String with Deletion-type Transmutation
Ryohei Nakano
Chubu University, 1200 Matsumoto-cho, Kasugai, 487-8501, Japan
Keywords:
Grammatical Induction, L-system, Error Correction, Transmutation.
Abstract:
L-system is a computational model to capture the growth process of plants. Once a noise-tolerant grammatical
induction called LGIC2 was proposed for deterministic context-free L-systems. LGIC2 induces L-system
grammars from a transmuted string mY, employing an emergent approach. That is, frequently appearing
substrings are extracted from mY to form grammar candidates. A grammar candidate can be used to generate
a string Z; however, the number of grammar candidates gets huge. Thus, LGIC2 introduced three pruning
techniques to narrow down candidates to get only promising ones. Candidates having the strongest similarities
between mY and Z are selected as the final solutions. So far, LGIC2 has been evaluated for replacement- and
insertion-type transmutations. This paper evaluates the performance of LGIC2 for deletion-type transmutation,
after slightly modifying the method.
1 INTRODUCTION
L-system was introduced by Lindenmayer as a com-
putational model to capture the growth process of
plants (Prusinkiewicz and Lindenmayer, 1990). The
central concept of L-system is rewriting, and the rela-
tionship with fractals led L-systems to various practi-
cal applications (Prusinkiewicz and Hanan, 1989).
The reverse process of rewriting is grammati-
cal induction (GI), which discovers grammars from
strings. Induction of L-system grammars has been lit-
tle explored so far. A survey paper (Higuera, 2005)
suggested that for many applications it is necessary
to be able to cope with noise, but most grammatical
inference algorithms are not robust to noise.
L-systems can be classified using two aspects:
(1) deterministic or stochastic, and (2) context-free
or context-sensitive. Deterministic context-free L-
system is the simplest, but very useful class.
Recent research on induction of deterministic
context-free L-system is summarized below. A
fast induction method called LGIN1 (L-system GI
based on Number theory, ver.1) was once proposed
(Nakano and Yamada, 2010), employing the num-
ber theory. However, it cannot cope with a trans-
muted string. Here, as for transmutation, we consider
r(eplacement)-type, i(nsertion)-type, d(eletion)-type,
or m(ixed)-type. To cope with a transmuted string,
an enumerative method called LGIC1 (L-system GI
with error Correction, ver.1) was proposed (Nakano
and Suzumura, 2012), where combinations of param-
eter values are enumerated to form grammar candi-
dates. It worked well for r-type with low transmuta-
tion rate, but did not work for i-type or high rate r-type
(Nakano, 2013a).
Then, an emergent method called LGIC2 (LGIC,
ver.2) was proposed (Nakano, 2013b), where fre-
quently appearing substrings are extracted from a
transmuted string to form grammar candidates. In
the method, the number of grammar candidates gets
huge; thus, three pruning techniques were introduced.
LGIC2 worked very nicely for r-type and i-type, over-
coming the drawback of LGIC1.
This paper evaluates the performance of LGIC2
for deletion-type transmutation, after slightly modi-
fying the method to fit this type.
2 BACKGROUND
D0L-system
The deterministic context-free L-system is called
D0L-system, defined as G = (V,C, ω,P), whereV and
C are sets of variables and constants, ω is an initial
string called axiom, and P is a set of production rules.
A variable is replaced in rewriting, while a constant
remains unchanged and controls turtle graphics.
397
Nakano R..
Emergent Induction of L-system Grammar from a String with Deletion-type Transmutation.
DOI: 10.5220/0005149703970402
In Proceedings of the International Conference on Knowledge Discovery and Information Retrieval (KDIR-2014), pages 397-402
ISBN: 978-989-758-048-2
Copyright
c
 2014 SCITEPRESS (Science and Technology Publications, Lda.)

In this paper we consider the following D0L-
system having two rules. Here n denotes the number
of rewritings, while A and B denote variables.
axiom : A, n =?
rule A : A →?????
rule B : B →???????
We have three strings: Y, mY, and Z. Y is a normal
string generated using the original grammar, while
mY is a string generated by applying transmutation to
Y. Z is a string generated using a grammar candidate,
where a grammar candidate means a candidate set of
n, rules A and B.
Transmutation
Among four types of transmutation, only d-type is
considered here since we want to know how LGIC2
works for d-type. We assume transmutation occurs
locally around the center of Y, considering two rates:
coverage rate P
c
and occurrence rate P
o
. P
c
rep-
resents the proportion of transmutation area to the
whole Y, while P
o
represents the probability of trans-
mutation in the area. Thus, overall transmutation rate
P
t
is calculated as follows:
P
t
= P
c
× P
o
(1)
Valid Transmutation
Simple transmutation will generate an invalid string,
which means such a string cannot be drawn through
turtle graphics. To keep the transmutation valid, the
numbers of left and right square brackets are moni-
tored and controlled if necessary. That is, in the trans-
mutation area the number count
ℓ
of left square brack-
ets should be larger than or equal to the number count
r
of right ones. Moreover,when the transmutation ends,
we assure count
ℓ
= count
r
by adding the right brack-
ets if necessary. Using such control, we get a valid
transmuted string mY from the normal string Y.
3 LGIC2: EMERGENT
INDUCTION OF L-system
GRAMMAR
An emergent induction method LGIC2 (L-system
GI with error Correction, ver.2) (Nakano, 2013b) is
explained and slightly modified. Given a transmuted
string mY, LGIC2 generates grammar candidates,
aiming at discovering the original grammar.
Basic Framework
The basic framework of LGIC2 is simple. Since a
right side of each production rule appears repeatedly
in mY, we extract frequently appearing substrings
from mY to form rule candidates. Then such a rule
candidate is combined with its reasonable n, the num-
ber of rewritings, to form a grammar candidate.
The main drawback of this approach is the
combinatorial growth in the number of grammar
candidates. Without any pruning it took ten days
to finish two thirds of the processing for mY whose
length is about 4,000. Thus, we need to narrow
down candidates to get only promising ones. LGIC2
introduces the following three pruning techniques.
Pruning by Frequency
Since the right side of each original rule appears
many times in mY, we can discard less frequent
substrings whose frequency is less than min
frq. The
threshold value may depend on the length of mY. In
our experiments we use min
frq = 50
The Number of Rewritings
Now that we have a pair of rule candidates, we con-
sider how to determine n, the number of rewritings.
The suitable n will depend on a transmutation type.
For r-type or i-type we tried to find n generating the
longest Z which satisfies len(Z) ≤ len(mY) since
len(Y) ≤ len(mY). For d-type, however, the situation
is different since len(mY) < len(Y). Thus, we should
select n generating the shortest Z which satisfies
len(mY) < len(Z).
Pruning by Goodness of Fit
The goodness of fit is a statistical measure which
evaluates how well a model (Z) fits to observed data
(mY). The goodness of fit can be evaluated by χ
2
val-
ues. Let the numbers of symbol occurrences in mY
and Z be {y
i
} and { z
i
} respectively. Then calculate
{p
i
= z
i
/len(Z)}, and we have the following χ
2
value.
Here I is the number of all kinds of variables and con-
stants.
χ
2
=
I
∑
i
(y
i
− len(mY) × p
i
)
2
/(len(mY) × p
i
) (2)
We discard a grammar candidate if χ
2
is greater than
max
chi2. For r-type or i-type transmutation we used
max chi2 = 150 since the value gets very large, more
than 200 for high transmutation rate P
t
, even for the
original grammar. For d-type, however, the fitting
turned out to be extremely good. Thus, we can use a
very small value max
chi2 = 10 for d-type.
Similarity between Two Strings
As the similarity between two strings, LGIC2 em-
ploys the longest common subsequence (LCS) (Cor-
men, Leiserson and Rivest, 1990). Let LCS(S
1
,S
2
)
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
398

denote LCS of two strings S
1
and S
2
. Given two
strings we may have more than one LCSs, but the
length of each LCS is the same. Note that LCS can
cope with any type of transmutation. The length
of LCS can be found using dynamic programming.
Another measure Levenshtein distance (Levenshtein,
1966) will result in much the same result.
Pruning by Contractive Embedding
In complex data, the cost of evaluating the distance
between two objects is usually very high. Here we
calculate the similarity measure LCS between two
strings. Our experiments showed it takes about two
seconds to calculate one LCS if each string length is
around 4,000. Thus, the number of LCS calculations
should be kept as small as possible. We can achieve
this without false dismissals if we find suitable con-
tractive embedding (Hjaltason and Samet, 2000). As
such embedding we consider ubLCS, an upper bound
of len(LCS), defined as below.
ubLCS(mY,Z) =
∑
i
min(y
i
,z
i
) (3)
This ubLCS can be used to prune grammar can-
didates. We discard a grammar candidate if
ubLCS(mY,Z) < LCS(mY, Z
t
), where Z
t
is the string
generated by the t-th best grammar candidate found
so far. Here t is given as the number of final best
solutions.
Procedure of LGIC2 Method
LGIC2 has the following four system parameters:
max rsl: maximum length of rule right side
min frq: minimum frequency of rule right side
max
chi2: maximum χ
2
value
tops: the number of final best solutions
LGIC2 goes as below:
(step 1) Extract a substring rs
1
from mY as a right side
candidate of rule A. Here the length of rs
1
should sat-
isfy 2 ≤ len(rs
1
) ≤ max
rsl, and the number of rs
1
occurrences in mY should be more than or equal to
min
frq.
(step 2) Eliminate any occurrences of rs
1
from mY
to get mYrest, and then extract a substring rs
2
from
mYrest as a right side candidate of rule B. Here the
length of rs
2
should satisfy 2 ≤ len(rs
2
) ≤ max
rsl,
and the number of rs
2
occurrences in mYrest should
be more than or equal to min
frq.
(step 3) For each pair of rs
1
and rs
2
selected above,
find the number of rewritings n to generate a string
Z. Here n is selected to be the smallest integer which
satisfies len(mY) ≤ len(Z).
(step 4) Calculate χ
2
value using mY and Z, and
then discard the grammar candidate as inappropriate
if χ
2
> max
chi2.
(step 5) Calculate ubLCS(mY, Z), the upper bound of
LCS(mY, Z), and then discard the grammar candidate
if ubLCS(mY,Z) < LCS(mY,Z
t
). Here Z
t
is the string
generated by the t-th best grammar found so far, and
note that t = tops.
(step 6) Calculate LCS(mY,Z), and then keep the
grammar candidate if the LCS is within best tops at
that time. Go to step 1 if there is another candidate.
(step 7) Output tops candidates having the largest
LCSs as the final solutions.
4 EXPERIMENTS
LGIC2 was evaluated using a transmuted plant model.
A plant model ex05n, a slight variation of brack-
eted OL-system example (Prusinkiewicz and Linden-
mayer, 1990), was used as a normal model in our ex-
periments. Figure 1 shows ex05n whose string length
is 4,243. PC with Xeon(R), 2.66GHz, dual was used
in our experiments.
(ex05n) n = 6, axiom : X
rule : X → F[+X][−X]FX
rule : F → FF
Figure 1: Normal plant model ex05n.
Here, we considered only d(eletion)-type trans-
mutation with combinations of three coverage rates P
c
= 0.25, 0.5, 0.75 and four occurrence rates P
o
= 0.25,
0.5, 0.75, 1.00. For each combination we transmuted
the normal model of ex05n five times changing a seed
for random number generator.
Following the description given in the previous
section, LGIC2 system parameters were set as fol-
lows: max rsl = 15, min frq = 50, max chi2 = 10,
and tops = 30.
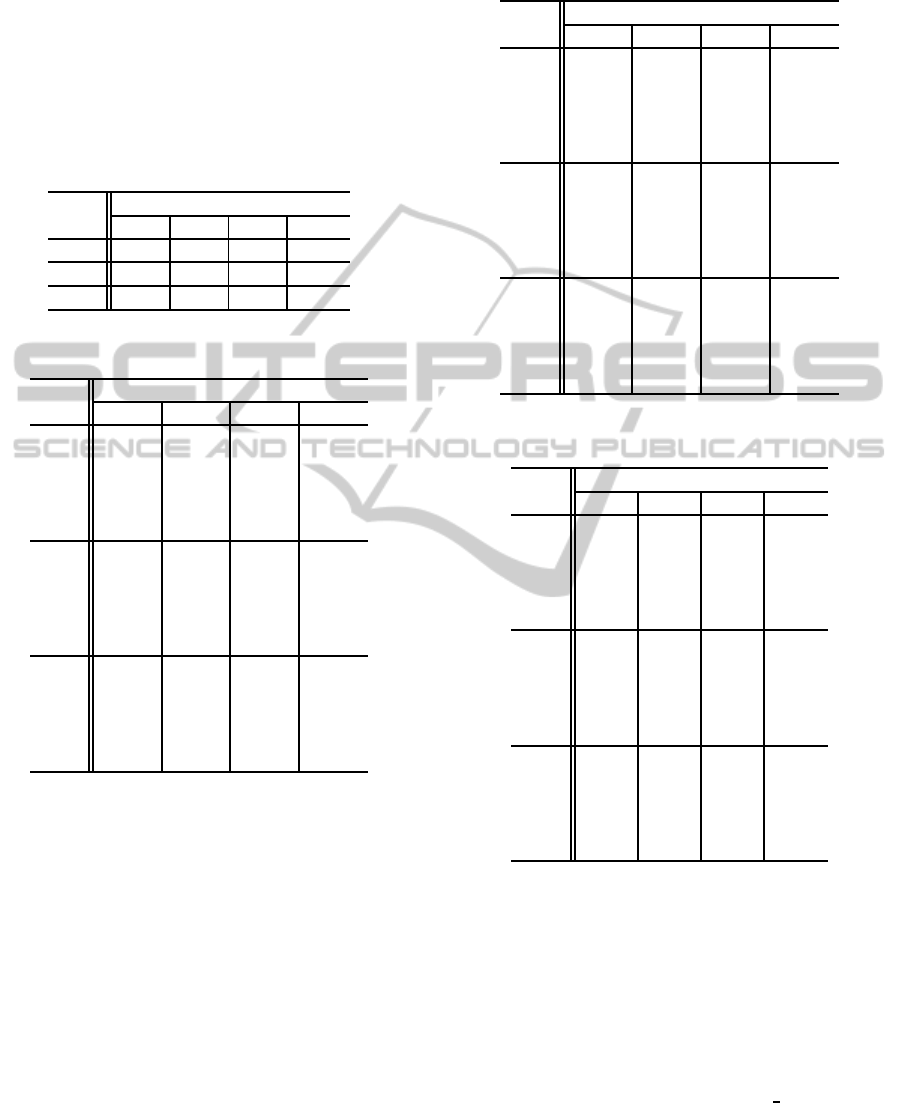
Table 1 shows the success rates of LGIC2 for d-
EmergentInductionofL-systemGrammarfromaStringwithDeletion-typeTransmutation
399

type transmutation. LGIC2 almost perfectly discov-
ered the original grammar; however, for the case of
P
c
= 0.75 and P
o
= 1.00, although the correct rules
were found successfully, the number of rewritings n
was found to be 5 instead of 6 because the length of
mY was 1,064, too short to find the correct n = 6.
Table 2 shows the length of mY for d-type trans-
mutation. Note again the length of Y is 4,243.
Table 1: Success rates of LGIC2 for d-type transmutation.
P
o
P
c
0.25 0.50 0.75 1.00
0.25 5/5 5/5 5/5 5/5
0.50 5/5 5/5 5/5 5/5
0.75 5/5 5/5 5/5 (5/5)
Table 2: Length of mY transmuted in d-type.
P
o
P
c
0.25 0.50 0.75 1.00
3,974 3,711 3,433 3,188
3,988 3,696 3,423 3,188
0.25 3,982 3,733 3,465 3,188
4,000 3,709 3,467 3,188
3,956 3,724 3,455 3,188
3,719 3,216 2,625 2,128
3,694 3,142 2,604 2,128
0.50
3,691 3,190 2,670 2,128
3,721 3,158 2,656 2,128
3,709 3,245 2,688 2,128
3,496 2,723 1,829 1,064
3,455 2,632 1,817 1,064
0.75
3,436 2,657 1,885 1,064
3,446 2,640 1,892 1,064
3,452 2,693 1,891 1,064
Table 3 shows the length of LCS between mY
transmuted in d-type and normal Y. Note that the
normal Y is nothing but the string Z generated by
the original grammar. We can see the length of
LCS(mY,Z(=Y)) is very close to the length of mY,
very often exactly the same for high P
o
.
Table 4 shows the ranking of the original grammar
among the final solutions. In most cases the original
grammar was found as No.1 candidate, which indi-
cates LCS is surely an excellent measure of the simi-
larity between two strings.
Figure 2 shows a plant model transmuted in d-type
with P
c
= 0.50 and P
o
= 0.50. The plant model has
rather bad-looking parts due to probabilistic deletion
around the center of its string. Figure 3 shows another
model transmuted in d-type with P
c
= 0.25 and P
o
=
1.00. This model has some branches chopped down
because a train of deletions occurred with P
o
= 1.00.
Table 3: Length of LCS between mY transmuted in d-type
and normal Y.
P
o
P
c
0.25 0.50 0.75 1.00
3,965 3,702 3,433 3,188
3,975 3,692 3,423 3,188
0.25 3,981 3,730 3,465 3,188
3,989 3,702 3,467 3,188
3,962 3,717 3,455 3,188
3,709 3,209 2,624 2,128
3,681 3,115 2,604 2,128
0.50 3,681 3,180 2,667 2,128
3,714 3,148 2,655 2,128
3,698 3,224 2,687 2,128
3,479 2,719 1,829 1,064
3,423 2,601 1,817 1,064
0.75
3,426 2,655 1,885 1,064
3,433 2,609 1,889 1,064
3,437 2,691 1,891 1,064
Table 4: Ranking of the original grammar for d-type trans-
mutation.
P
o
P
c
0.25 0.50 0.75 1.00
No.3 No.1 No.1 No.1
No.4 No.1 No.1 No.1
0.25
No.3 No.1 No.1 No.1
No.4 No.1 No.1 No.1
No.3 No.1 No.1 No.1
No.1 No.1 No.2 No.1
No.1 No.1 No.2 No.1
0.50 No.1 No.1 No.2 No.1
No.1 No.1 No.2 No.1
No.1 No.1 No.1 No.1
No.1 No.1 No.1 No 3
No.1 No.1 No.1 No.3
0.75 No.1 No.1 No.1 No.3
No.1 No.1 No.1 No.3
No.1 No.1 No.1 No.3
Even from these transmuted plants, LGIC2 success-
fully discovered the original grammar.
Table 5 shows χ
2
value calculated from normal Y
and transmuted mY. Note that χ
2
values for r-type or
i-type transmutation are very large for most cases, and
exceed 100 for high transmutation rate P
t
. However,
χ
2
value for d-type is quite small probably because
occurrence rates of strings will not change drastically
even if large deletion may happen. This nature can be
used for pruning; thus, we adopted max
chi2 = 10.
Table 6 shows the average CPU time of LGIC2 for
d-type transmutation. For each P
c
, average CPU time
gets shorter as P
o
gets larger, and for each P
o
, average
CPU time gets shorter as P
c
gets larger. These ten-
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
400

Figure 2: Plant model transmuted in d-type (P
c
= 0.50, P
o
=
0.50).
Figure 3: Plant model transmuted in d-type (P
c
= 0.25, P
o
=
1.00).
dencies can be understood if we consider larger trans-
mutation rate P
t
(= P
c
× P
o
) makes transmuted string
mY shorter, which will reduce the number of different
substrings extracted from mY.
Table 7 shows the average number of LCS calcu-
lations for d-type transmutation. For each P
o
, average
number of LCS calculations gets smaller as P
c
gets
larger. We consider the above discussion may explain
this tendency. Overall, the average numbers of LCS
calculations are very small due to our pruning.
From our experiments described above, we can
say that an emergent approach of LGIC2 together
with pruning techniques works very well for d-type
transmutation.
5 CONCLUSION
This paper examined how a noise-tolerant emergent
induction LGIC2 works for d-type transmutation.
Table 5: χ
2
value calculated from normal Y and mY trans-
muted in d-type.
P
o
P
c
0.25 0.50 0.75 1.00
0.887 0.974 1.059 0.652
0.210 0.468 0.219 0.652
0.25 0.757 0.657 0.886 0.652
0.130 0.248 0.126 0.652
0.170 0.252 0.664 0.652
0.642 0.269 0.775 0.104
1.044 2.663 0.841 0.104
0.50
0.302 0.394 0.881 0.104
1.177 0.669 1.218 0.104
1.604 0.951 0.202 0.104
1.263 2.813 1.005 5.350
1.250 0.695 2.383 5.350
0.75
0.287 4.676 2.057 5.350
0.961 5.764 4.260 5.350
1.092 1.010 1.079 5.350
Table 6: Average CPU time (sec) of LGIC2 for d-type trans-
mutation.
P
o
P
c
0.25 0.50 0.75 1.00
0.25 923.8 791.1 546.0 283.2
0.50 551.5 431.0 246.2 61.3
0.75 433.2 287.4 143.6 18.0
Table 7: Average number of LCS calculations for d-type
transmutation.
P
o
P
c
0.25 0.50 0.75 1.00
0.25 28.0 26.8 31.2 31.0
0.50 6.8 7.8 7.0 8.0
0.75 6.8 4.4 5.6 5.0
LGIC2 was slightly modified to fit d-type transmu-
tation. Our experiments using a simple plant model
showed LGIC2 discovered the original grammar as a
top candidate for almost all cases in minutes for high
transmutation and in about 15 minutes at the low-
est transmutation. In the future we plan to apply the
method to other plant models.
ACKNOWLEDGEMENTS
This work was supported by Grants-in-Aid for Sci-
entific Research (C) 25330294 and Chubu University
Grant 26IS19A.
EmergentInductionofL-systemGrammarfromaStringwithDeletion-typeTransmutation
401

REFERENCES
Cormen, T. H., Leiserson, C. E. and Rivest, R. L. (1990).
Introduction to algorithms. MIT Press.
Higuera, C. de la. (2005). A bibliographical study of gram-
matical inference. Pattern Recognition, 38:1332–
1348.
Hjaltason, G.R. and Samet, H. (2000). Contractive em-
bedding methods for similarity searching in metric
spaces. CS-TR-4102, Univ. of Maryland.
Levenshtein, V. (1966). Binary codes capable of correct-
ing deletions, insertions, and reversals. Soviet Physics
Doklady, 10(8):707–710.
Nakano, R. (2013a). Error correction of enumerative induc-
tion of deterministic context-free L-system grammar.
IAENG Int. Journal of CS, 40(1):47–52.
Nakano, R. (2013b). Emergent induction of deterministic
context-free L-system grammar. Advances in Intelli-
gent Systems and Computing 237, pp. 75–84.
Nakano, R. and Suzumura, S. (2012). Grammatical induc-
tion with error correction for deterministic context-
free L-systems. In WCECS 2012, pp. 534–538.
Nakano, R. and Yamada, N. (2010). Number theory-
based induction of deterministic context-free L-
system grammar. In KDIR 2010, pp. 194–199.
Prusinkiewicz, P. and Hanan, J. (1989). Lindenmayer sys-
tems, fractals, and plants. Springer-Verlag, New York.
Prusinkiewicz, P. and Lindenmayer, A. (1990). The algo-
rithmic beauty of plants. Springer-Verlag, New York.
KDIR2014-InternationalConferenceonKnowledgeDiscoveryandInformationRetrieval
402