
Critical Position Identification in Games and Its Application to
Speculative Play
Mohd Nor Akmal Khalid
1
, Umi Kalsom Yusof
1
, Hiroyuki Iida
2
and Taichi Ishitobi
2
1
School of Computer Sciences, Universiti Sains Malaysia, 11800 Georgetown, Pulau Pinang, Malaysia
2
School of Information Science, Japan Advance Institute of Science and Technology,
1-1 Asahidai, Nomi, Ishikawa 923-1292, Japan
Keywords:
Speculative Play, Critical Position, Games.
Abstract:
Research in two-player perfect information games have been one of the focus of computer-game related studies
in the domain of artificial intelligence. However, focus on an effective search program is insufficient to give
the “taste” of actual entertainment in the gaming industry. Instead of focusing on effective search algorithm,
we dedicate our study in realizing the possibility of applying speculative play. However, quantifying and
determining this possibility is the main challenge imposed in this study. For this purpose, the Conspiracy
Number Search algorithm is considered where the maximum and minimum conspiracy numbers are recorded
in the test bed of a simple Tic-Tac-Toe game application. We analyze these numbers as the measures of
critical position identifier which determines the right moment for possibility of applying speculative play
through operators formally defined in this article as ↑ tactic and ↓ tactic. Interesting results are obtained with
convincing evidences but further works are still needed in order to prove our hypothesis.
1 INTRODUCTION
In the domain of speculative play, understanding the
the game or mastering the game intricacy is the most
important aspect for achieving successful outcome
in the respective competitive combat (van den Herik
et al., 2005). However, the main challenge in the
domain of speculative play is to identify a (criti-
cal) position for applying a speculative play. The
opponent-model search (Iida et al., 1993; Carmel and
Markovitch, 1993; Iida et al., 1994) is such a specu-
lative play, but without the knowledge of when is the
most optimum position to apply it during a game. In
other words, determining when one should change his
strategy from minimax to any speculative way is the
puzzling issue.
The mechanics of computer-games in two-player
perfect information games or two-player games in
short, such as board games (e.g. tic-tac-toe, othello,
checkers, chess, etc.), involve using a tree searching
algorithm to evaluate and decide the possible moves
to take. However, even in the best known search al-
gorithms, the search space possesses exponential time
complexity with the growingdepth of the tree (Lorenz
et al., 1995). Innovative search algorithms, search en-
hancements, and learning ideas have been applied by
ample research efforts towards creating a computer
program that dominates the games against their oppo-
nents with better strength and performance (Schaeffer
and van den Herikb, 2002), as well as overcoming the
time complexity limitation of the tree search (Kishi-
moto et al., 2012). In order to better understand the
nature of any computer-game, studying the progress
of the games is important for improving the game’s
value as a form of entertainment.
When progressing on the board game, different
positions made by a player throughout the game’s
time horizon can effect the outcome of the endgame.
Usually, playing well throughout the game when
competing against top human players is not enough
but playing optimally during the endgame (or certain
parts of the games) is very important (Jansen, 1992;
Donkers, 2003). Focusing on a certain stage of the
game is essential in order to apply different specula-
tive play to boost its excitement. However, the out-
come of the computer-games (lose, win, or draw) is
unclear until the game ends. Predicting this outcome
during the progress of computer-games is mainly de-
pendent on the likeliness of a position to result in ei-
ther winning, losing, or draw. This situation is for-
mally defined as critical position, where at a cer-
tain point of the game progress, the game outcome
38
Khalid M., Yusof U., Iida H. and Ishitobi T..
Critical Position Identification in Games and Its Application to Speculative Play.
DOI: 10.5220/0005179900380045
In Proceedings of the International Conference on Agents and Artificial Intelligence (ICAART-2015), pages 38-45
ISBN: 978-989-758-074-1
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

is measurable and eventually becomes certain and in-
evitable.
Identifying critical position of a progressing com-
puter game involve comprehending the computer
players tendencyof changing its strategy during a par-
ticular moment of the game play. In other words,
knowing the right moment of based on this critical
position at a certain state of the game enables the pos-
sibility of applying speculative play which essentially
produces interesting outcome of the game (Ramon
et al., 2002). Thus, identifying this critical position
is highly dependent on the quantifying capabilities of
the indicator. Therefore, a suitable search algorithm
that acts as an indicator during the games progress is
necessary in order to identify its critical position.
A well-known search indicators studied by sev-
eral researchers in the late-80s is the Conspiracy-
Number Search (CNS). Introduced by McAllester
(McAllester, 1985; McAllester, 1988), CNS is a best-
first search algorithm for minimax tree framework,
which determines the cardinality of the smallest set of
leaf nodes which have to “conspire” to change their
values in order to change the minimax value of the
root. This present a suitable opportunity for determin-
ing the moments for applying speculative play (e.g.
opponent model), thus acts as the motivating factor of
selecting CNS for this study. One of the ideas under-
lying CNS is that the distribution of the values over
the leaf nodes of the tree, and the shape of the tree,
should influence the selection of the next node to be
investigated (Kishimoto et al., 2012). However, fo-
cus on CNS as a search algorithm in computer-games
research was faced with discouraging results (Lorenz
et al., 1995; Schaeffer, 1989; Elkan, 1989; Schaef-
fer, 1990; van der Meulen, 1990). Later, Allis et al.
(Allis et al., 1994) derived and specialized CNS con-
cepts to the AND/OR tree framework where the study
matured into Proof-Number Search (PNS). Although
CNS is different compared to PNS, CNS’s conceptual
frameworks bear certain correlation to PNS.
This study concerns a matter of critical position
identification, not a matter of program strength im-
provement in games (See some approaches, e.g., done
by Jonathan Schaeffer). Hence, we have chosen a
game as simple as possible in order to clearly explain
the proposed idea. Further investigation would be, as
suggested, to implement the proposed idea in more
complicated games such as chess. To our best knowl-
edge, no other research has been done with CNs to
identify critical positions instead of using as game-
tree search heuristics (stability of the root node’s min-
imax value). In this paper, any part of speculativeplay
is not described. However, the relation between CN
and strategic change at critical position (in case where
the position is going to be disadvantageous position)
should be very important in the context of speculative
play.
2 CONSPIRACY-NUMBER
SEARCH
In the minimax tree framework, the first player tries
to maximize his or her advantage, while the second
player tries to minimize it (Neumann and Morgen-
stern, 1947; Shannon, 1950). CNS searches the tree
in a manner that at least c > 1 of the leaf values
have to change in order to change the decision at the
root (Lorenz et al., 1995). Intuitively, when expand-
ing a minimax tree further, the accuracy and stabil-
ity of the root value depend on how much it changes.
Major changes on the root value make it unreliable
(McAllester, 1988). Therefore, the concept of con-
spiracy is used to measure the root value’s stability
and its likelihood to change by narrowing the range
of the plausible values of the root (Schaeffer, 1989).
The likelihood of the root taking a particular value is
reflected in that value’s associated conspiracy num-
ber. This conspiracy number measures the size of the
“conspirators” needed to bring about a certain change
in root value; the more conspiratorsneeded for a given
change, the less likely the change (McAllester, 1988).
This is done by keeping track so the number of leaf
nodes whose value must be changed (when searched
deeper) to change the root’s node value by a certain
amount or taking on that new value. A change in the
value of a certain set of leaf nodes is called conspiracy
between those leaf nodes.
The algorithm is a probabilistic search in nature
where there is no guarantee that the correct solution
will be found when it terminates, but the most likely
one instead. The conceptual framework behind the
CNS is to grow search trees for which one has con-
fidence by measuring the number of value through
the conspiracy numbers. The search is guided in a
best first manner, where the tree searched so far is
kept in memory. An example is probably the best
way to illustrate the function of a conspiracy number.
The following is taken from (Schaeffer, 1989; Lorenz
et al., 1995): Assume that the branching factor is 2,
the range of values are from 1 to 6, the root node is
the MAX node, inside the nodes are their names and
their minimax values, and the simple tabular for stor-
ing conspiracy numbers of the root. From Fig. 1, it
can be observed that the leaves or terminal node have
to at least change their value to cause the value of the
root to become 1, 2, 4, 5, or 6. For example, only
leaf E has to change its value to 5 in order for the root
CriticalPositionIdentificationinGamesandItsApplicationtoSpeculativePlay
39
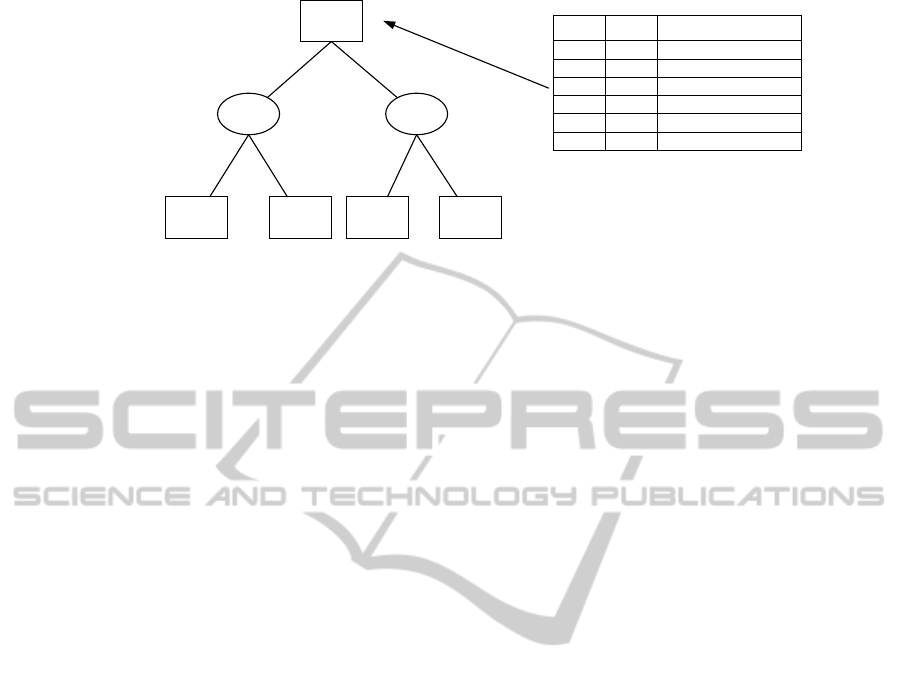
A=3
D=5 E=2 F=3 G=4
B=2 C=3
Root
Interior Node
Terminal Node
value cn conspirators
1 2 (D or E) and (F or G)
2 1 F or G
3 0
4 1 E or F
5 1 E
6 2 (D and E) or (F and G)
Figure 1: Illustration of a minimax tree adopting CNS algorithm.
value to become 5.
As described by Schaeffer (Schaeffer, 1989), there
is a simple method of computing the conspiracy num-
bers. At the terminal node t, the conspiracy number
associated with node t value is 0 and for all other val-
ues is 1. For the interior node, if the value x of a
MAX node is to be increased to x
′
> x, only one of
the successor nodes need to change its value to x’. It
is clear that the conspiracy number for x’ is the mini-
mum amongst all other successors. This is denoted as
↑ needed
i
. If the value x is to be decreased to x
′
< x,
all successors with values greater than x’ must change
their value to one lower than x’. That is the reason
why the number of conspirators for these nodes are
summed. This is denoted as ↓ needed
i
. The rules of
calculating conspiracy numbers are given as the fol-
lowing (v is the associated conspiracy number of the
node and m is the minimax value of the node):
CN(v) = 0, if v = m,
At MAX node:
CN(v) =
∑
all sons i
↓ needed
i
(v), for all v < m,
CN(v) = min
all sons i
↑ needed
i
(v), for all v > m.
At MIN node:
CN(v) = min
all sons i
↓ needed
i
(v), for all v < m,
CN(v) =
∑
all sons i
↑ needed
i
(v), for all v > m.
Since its introduction, variants of CNS have
been proposed by several researchers. α − β Con-
spiracy Search proposed by McAllester and Yuret
(McAllester and Yuret, 1993) establishes lower and
upper bound of the search. The MAX strategy estab-
lishes a lower bound and the MIN strategy establishes
an upper bound. Thus, the conspiracy numbers can
be used to measure the “safety” of these two strate-
gies. Lorenz et al. (Lorenz et al., 1995) proposed
a Controlled-Conspiracy Number Search where in-
stead of variable depth, an α − β quiescence search
is used and search bound is provided. The conspiracy
number vectors are compressed into 3-tuples, allow-
ing the CCNS to be independent of the granularity of
the evaluation function (e.g. positional play in chess).
3 CONSPIRACY-NUMBER
SEARCH AS CRITICAL
POSITION IDENTIFIER
Determining critical position is vitals due to the fol-
lowing reasons: First, the specific outcome of the
game can be estimated in advance (e.g. resignation)
and this estimation can be utilized for game outcome
prediction. Second, the critical positions are expected
to expose the possibilities of tactic changes, denoted
as ↑ tactics or ↓ tactics, respectively. The ↑ tactics
implies that the computer player tries to force a draw
when it’s losing, while ↓ tactics implies that the com-
puter player tries to force a draw when achieving a
win is impossible. Third, critical positions can be
used to estimate the moment for computer player to
apply speculative play and change the outcome of the
game.
However, why do we use CNS instead of the po-
sitional scoring (evaluation function) alone during the
game’s progression? The positional scoring act as a
guiding function for an individual player to determine
his/her state in the game’s progress (Buro, 1999). Al-
though it might be suitable for identifying critical po-
sitions, it still lack of the probabilistic element in ab-
stracting the player’s decision to determine the next
game state. Basically, positional scoring shows how
the game progresses (i.e. which player is leading the
game) but the CN-values potentially show its prob-
able changes. Thus, the goal of critical position is
to determine the possibility of improving or deteri-
orating the positional score value of a move (evalu-
ate for probable impact of next moves), while posi-
tional scoring makes use of the evaluation features
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
40
of a move (evaluate for probable gain of next moves)
(Buro, 1999).
3.1 Experimental Results and
Discussion
CNS requires two types of conspiracy numbers
needed to maintain, ↑ needed and ↓ needed. We con-
sider this as a scalar measures in the computer-game’s
search progress to analyze and justify the rationale of
the hypothesis mentioned earlier. A simple Tic-Tac-
Toe game is used as the test bed of our study.
This experiment is tested with fixed-depth mini-
max algorithm applying CNS as a scalar measures for
recording the conspiracy numbers of the root values
for each game moves. For every player X with search
depth i there is an opposing player O with search
depth j, where 2 ≤ i ≤ 6 and 2 ≤ j ≤ 6. Therefore,
there are 25 total game sets (both player X and player
O have five depths). Player X is assumed to be the
first player to start the game in every case, since if
player O starts the results will be just the reverse. The
rules of the games are as follows:
• For player O, the score is negative. For player X,
the score is positive.
• Player X tries to maximize the score, while player
O tries to minimize the score.
• For each row, if there are both X and O, then the
score for the row is 0.
• If the whole row is empty, then the score is 1.
• If there is only one X, then the score is 10. If there
is only one O, then the score is -10.
• If there are two X, then the score is 100. If there
are two O, then the score is -100.
• If there are 3 X, then the score is 1000. If there
are three O, then the score is -1000.
Table 1 and Table 2 shows the recorded maximum
conspiracy numbers (MaxCN) and minimum conspir-
acy numbers (MinCN) for every game sets, respec-
tively. The odd and even numbers (highlighted in light
gray) of the game’s progress are relevant to player X
and player O, respectively. In all cases of game sets,
the game outcomes is a draw. To counter this, we con-
sider the final score of any player as win, lose, or draw
as final score of 100, -100, and 0, respectively. Table
3 shows the final scores of every game of player X
versus player O.
Observing Table 1 and Table 2, the MaxCN of
player X decreases steadily (in most cases) while the
MaxCN for player O decreases abruptly. To sim-
plify the results interpretation, the following rules are
adopted: The MaxCN of current player p is consid-
ered abruptly decreased if |MaxCN
p
i+1
−MaxCN
p
i
| >
|MaxCN
p
i+1
|, where i equals to the game progress
Table 1: Maximum Conspiracy numbers of player X against
player O with depth variations.
Maximum Conspiracy Numbers
Depth Game Progress
(p1,p2) 1 2 3 4 5 6 7 8 9
2,2 8 7 6 5 4 3 2 1 1
2,3 8
22 6 8 4 4 2 1 1
2,4 8
62 6 16 4 4 2 1 1
2,5 8
128 6 17 4 4 2 1 1
2,6 8
288 6 17 4 4 2 1 1
3,2 56 7 26 5 10 3 2 1 1
3,3 56
22 26 8 10 5 2 1 1
3,4 56
62 26 16 10 5 2 1 1
3,5 56
128 26 17 10 5 2 1 1
3,6 56
288 26 17 10 5 2 1 1
4,2 136 7 89 5 17 3 2 1 1
4,3 136
22 89 8 17 3 2 1 1
4,4 136
62 89 16 17 3 2 1 1
4,5 136
128 89 17 17 3 2 1 1
4,6 136
288 89 17 17 3 2 1 1
5,2 360 7 206 5 17 3 2 1 1
5,3 360
22 206 8 17 3 2 1 1
5,4 360
62 206 16 17 3 2 1 1
5,5 360
128 206 17 17 3 2 1 1
5,6 360
288 206 17 17 3 2 1 1
6,2 648 7 295 5 17 3 2 1 1
6,3 648
22 295 8 17 3 2 1 1
6,4 648
62 295 16 17 3 2 1 1
6,5 648
128 295 17 17 3 2 1 1
6,6 648
288 295 17 17 3 2 1 1
p1 = player X, p2 = player O
(e.g. moves). The value of MaxCN implies insta-
bility and changes in the root value is more likely. In
other words, possibility of losing or winning is high
since the likeliness of the root value to change is high.
However, the fact that the outcome is inevitable (ei-
ther win or lose) but not known, this stage simulates
the critical position which is highly recommended for
applying speculative play.
For MinCN, however, a different interpretation is
needed. The abruptly decreased MinCN utilizes the
same rule as MaxCN: The MinCN of current player
p is considered abruptly decreased if |MinCN
p
i+1
−
MinCN
p
i
| > |MinCN
p
i+1
|, where i equals to the
game’s progress (e.g. moves). This situation is
the critical position for tactic changes (↑ tactic or
↓ tactic). In the case of abrupt inclining of MaxCN,
the root value stabilizes and tactic change of the cur-
rent player from better to worst (from winning to a
draw or a draw to losing) is more likely. This particu-
lar situation is when the ↓ tactic occurs. In the case of
abrupt inclining of MinCN, the root value is limited to
the available MinCN value only. Thus, this situation
implies the likelihood of identifying the tactic change
of the current player from worst to better (from losing
to a draw or from a draw to winning). This particular
CriticalPositionIdentificationinGamesandItsApplicationtoSpeculativePlay
41

Table 2: Minimum Conspiracy numbers of player X against
player O with depth variations.
Minimum Conspiracy Numbers
Depth Game Progress
(p1,p2) 1 2 3 4 5 6 7 8 9
2,2 1 6 1 4 1 3 0 0 0
2,3 1
4 1 4 1 1 0 0 0
2,4 1
13 1 8 1 0 0 0 0
2,5 1
13 1 5 1 0 0 0 0
2,6 1
23 1 1 1 0 0 0 0
3,2 6 6 4 4 0 0 0 0 0
3,3 6
4 4 4 0 0 0 0 0
3,4 6
13 4 8 0 0 0 0 0
3,5 6
13 4 5 0 0 0 0 0
3,6 6
23 4 1 0 0 0 0 0
4,2 4 6 3 4 1 3 0 0 0
4,3 4
4 3 4 1 1 0 0 0
4,4 4
13 3 8 1 0 0 0 0
4,5 4
13 3 5 1 0 0 0 0
4,6 4
23 3 1 1 0 0 0 0
5,2 13 6 5 4 0 3 0 0 0
5,3 13
4 5 4 0 1 0 0 0
5,4 13
13 5 8 0 0 0 0 0
5,5 13
13 5 5 0 0 0 0 0
5,6 13
23 5 1 0 0 0 0 0
6,2 13 6 5 4 0 3 0 0 0
6,3 13
4 5 4 0 1 0 0 0
6,4 13
13 5 8 0 0 0 0 0
6,5 13
13 5 5 0 0 0 0 0
6,6 13
23 5 1 0 0 0 0 0
p1 = player X, p2 = player O
Table 3: Final scores based on depths of player X against
player O.
Final Score
Player O
2 3 4 5 6
2 0 0 0 0 0
3 0 0 0 0 0
Player X 4 -100 -100 -100 -100 -100
5 -100 -100 -100 -100 -100
6 -100 -100 -100 -100 -100
situation is when the ↑ tactic occurred.
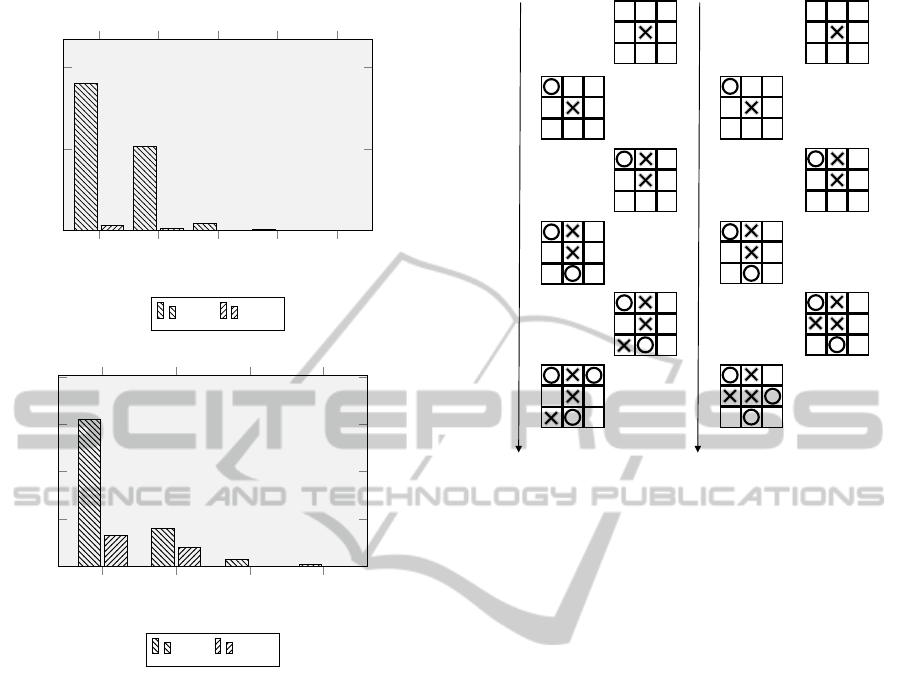
For instance, consider player X with search depth
2 against player O with search depth 3. Generally,
player O can be regarded to outperform player X
due to lookahead superiority. Figure 2 and Figure
4(a) simulates the mentioned game’s progress situ-
ation. During the first move, player X chooses the
middle position of the board leaving player O with
limited options. The MaxCN and MinCN of player
X is currently 8 and 1 respectively. After consid-
ering the vertical, diagonal, and horizontal spaces,
player O chooses the upper left corner of the board
Table 3: Final scores based on depths of player X against
2 3 4 5 6
0 0 0 0 0
0 0 0 0 0
-100 -100 -100 -100 -100
-100 -100 -100 -100 -100
-100 -100 -100 -100 -100
of the current player from worst to better (from losing
to a draw or from a draw to winning). This particular
For instance, consider player X with search depth
2 against player O with search depth 3. Generally,
player O can be regarded to outperform player X
due to lookahead superiority. Figure 2 and Figure
4(a) simulates the mentioned game’s progress situ-
ation. During the first move, player X chooses the
middle position of the board leaving player O with
1 2 3 4
5
0
2
4
6
8
10
8
6
4
2
11 1 1
0 0
Moves
Player X with search depth 2
Max
Min
1 2 3 4
0
10
20
22
8
4
1
4 4
1
0
Moves
Player O with search depth 3
Max
Min
Figure 2: MaxCN and MinCN for player X with search
depth 2 against player O with search depth 3
Figure 2: MaxCN and MinCN for player X with search
depth 2 against player O with search depth 3.
and currently possess MaxCN and MinCN of 22 and
4 respectively. Consequently, player X chose the up-
per middle side of the board, which effects MaxCN
to decrease steadily, while MinCN remain the same.
Next, player O chooses the lower middle of the board
which abruptly reduces player O’s MaxCN to 8 while
MinCN remains the same. This situation imposes that
player O is in a critical position, even if its intent is
to prevent player X from winning. Therefore, player
O is in the state of ↓ tactic and is advised to apply
different tactic. In the next move, player X chooses
the lower left corner of the board which has forced
player O into another bad position. During the con-
sequent move, player O’s MaxCN reduces steadily
while MinCN is abruptly reduced to 1, which implies
that player O has applied ↑ tactic where, instead of
losing, it tries to force player X into a draw. Thus, the
final outcome of the game is a draw.
Another example is the case of player X with
search depth 5 against player O with search depth 4
which is given in Figure 3 and Figure 4(b). During
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
42
1 2 3 4
5
0
200
400
360
206
17
2
1
13
5
0 0 0
Moves
Player X with search depth 5
Max
Min
1 2 3 4
0
20
40
60
80
62
16
3
1
13
8
0 0
Moves
Player O with search depth 4
Max
Min
Figure 3: MaxCN and MinCN for player X with search
depth 5 against player O with search depth 4
Figure 3: MaxCN and MinCN for player X with search
depth 5 against player O with search depth 4.
the first move, player X chooses the middle position
of the board leaving player O with limited options.
The MaxCN and MinCN of player X is currently 360
and 4 respectively. The high value of MaxCN is be-
cause of the deeper search depths. In the next move,
player O chooses the upper left corner of the board
and obtains a MaxCN and MinCN of 62 and 13 re-
spectively. Consequently, player X chooses the upper
middle side of the board, making MaxCN and MinCN
decreases steadily. During the rest of the moves, the
evolution of MaxCN of both player X and player O
abruptly reduces, forcing both players into “dilem-
mas” where both ↓ tactic and ↑ tactic occur. This situ-
ation can be hypothetically defined as the state where
both players are able to apply different tactics. On the
other hand, observing the MinCN of both player X
and player O during fifth and sixth moves implies that
both player adopted the ↓ tactic. However, player O’s
leading score plays its part and forces player X to lose
the game (assumed final score is winning).
The challenge in the study of speculative play is
to identify critical positions at which one should con-
WůĂLJĞƌy
DĂdžE͗ϴ
DŝŶE͗ϭ
WůĂLJĞƌy
DĂdžE͗ϲ
DŝŶE͗ϭ
WůĂLJĞƌy
DĂdžE͗ϰ
DŝŶE͗ϭ
WůĂLJĞƌK
DĂdžE͗ϮϮ
DŝŶE͗ϰ
WůĂLJĞƌK
DĂdžE͗ϴ
DŝŶE͗ϰ
WůĂLJĞƌK
DĂdžE͗ϰ
DŝŶE͗Ϭ
DŽǀĞ
ϭ
DŽǀĞ
Ϯ
DŽǀĞ
ϯ
DŽǀĞ
ϰ
DŽǀĞ
ϱ
DŽǀĞ
ϲ
WůĂLJĞƌy
DĂdžE͗ϯϲϬ
DŝŶE͗ϰ
WůĂLJĞƌy
DĂdžE͗ϮϬϲ
DŝŶE͗ϯ
WůĂLJĞƌy
DĂdžE͗ϭϳ
DŝŶE͗ϭ
WůĂLJĞƌK
DĂdžE͗ϲϮ
DŝŶE͗ϭϯ
WůĂLJĞƌK
DĂdžE͗ϭϲ
DŝŶE͗ϱ
WůĂLJĞƌK
DĂdžE͗ϯ
DŝŶE͗Ϭ
;ĂͿ ;ďͿ
Figure 4: Simulation of Tic-Tac-Toe games.
sider to apply a kind of speculative strategy such as
opponent-model search in order to change the situa-
tion: from behind to even or better. Another chal-
lenge in GM-level man-machine matches is to iden-
tify (no more promising) positions to resign. There-
fore, the experiments suggested in this study provide
the main foundation for identifying the critical posi-
tions, although further investigation is expected.
4 CNS CORRELATIONS TO PNS
Application of PNS in the previous work such as
(Ishitobi et al., 2013) raised questions whether any
correlations exists in the application of CNS as a criti-
cal position identifier. Theoretically, experimental re-
sults obtained from the previous section empowered
the possibility of correlation between CNS and PNS
as indicators in their respective tree search frame-
work. This section attempts to identify that correla-
tion and give a better picture on the importance of
these two indicators. The following section will give
a short description on the basis of PNS.
4.1 The Basis of PNS
PNS, like its ancestor CNS, is a best-first search al-
gorithm in which the tree searched so far is stored
in memory. The main difference is that PNS aims
at proving the true value of root, where the interim
minimax values are not considered (Allis et al., 1994).
CriticalPositionIdentificationinGamesandItsApplicationtoSpeculativePlay
43

The PNS heuristic determines the most promising leaf
by selecting a most-proving node or most-promising
node (MPN), which can contribute to either a proof
or a disproof of the root if a leaf node is solved. The
MPN can be formally defined as the node which, with
the least possible effort, potentially contributes most
to the establishment of the minimax value of the root.
The MPN can be found by manipulating two criteria
of the search tree: (1) its shape (determined by the
branching factor of every internal node), and (2) the
values of the leaves. The basic and un-enhanced PNS
is an uninformed search method that does not require
any game-specific knowledge beyond its rules (Kishi-
moto et al., 2012).
The PNS produces two special values for each
node n in order to find MPN. First, the proof num-
ber (denoted as pn(n) where pn is the proof number
of node n) which is the smallest number of leaf nodes
in the subtree starting with n that have to be proven
in order to prove that n is a win. Second, the disproof
number (denoted as dn(n) where dn is the disproof
number of node n) which is the minimum number of
leaf nodes that have to be disproved in order to prove
that n is a loss.
Calculating the values of pn and dn for each node
in the tree is performed in a bottom-up manner. Usu-
ally, In a terminal node t, the game-theoretic value
is known or the corresponding position has no legal
moves. If t is a win, then pn(t) = 0 and dn(t) = 1.
If t is a loss, then pn(t) = 1 and dn(t) = 0. If t is un-
known, then pn(t) = dn(t) = 1. In this case, thetermi-
nal node t is called a temporary terminal node. For the
internal MAX node, it is sufficient to have one child
that proves the value of v. The pn of a MAX node is
equal to the minimum of the pn of its children. For
dn, the only way to disprove v is to disprove v for all
its children. So, the dn for MAX node is equal to the
sum of the dn of all its children. It is the reverse for
the internal MIN node.
However, PNS is famously known for searching
the AND/OR tree framework instead of the minimax
tree framework. The AND/OR tree is a type of tree
where the nodes have only three possible values: true,
false, and unknown(Ishitobi et al., 2013). Using PNS,
the pn for an AND/OR tree represents the minimum
number of unsolved leaf nodes that need to be solved
in order to win in the root. Similarly, the dn for an
AND/OR tree represents the minimum number of un-
solved leaf nodes that need to be solved in order to
lose in the root. The PNS always considers the MPN
in which the internal nodes can be decided recursively
if the terminal node value was decided. Thus, PNS
can be used to decide the value of the root node by
deciding values of other nodes as soon as possible
(Ishitobi et al., 2013).
4.2 General Correlation of the Elements
of CNS and PNS
As described by Ishitobi et al. (Ishitobi et al., 2013),
pn is related to the difficulty, which relates to the
minimum number of unsolved nodes that need to be
solved. So, maximum pn shows the complexity to
solve these unsolved nodes. On the other hand, dn
is related to the minimum number of unsolved nodes
that need to be disproved. Therefore, maximum dn
shows the complexity to disprove. In other word, both
the maximum pn and maximum dn are an effective
measures of difficulty to solve nodes as soon as pos-
sible for the AND/OR tree framework.
The MaxCN and MinCN show a correlation to
maximum pn and maximum dn in the minimax tree
framework. In the CNS context, MaxCN and MinCN
identify the critical position in the game’s progress
for an expected outcome. MaxCN indicates the un-
likeliness of root value in achieving a value. There-
fore, high value of MaxCN implies the high likeliness
of winning or losing. MinCN indicates that the like-
liness of root value to achieve a value is limited to
the value of MinCN. So, high value of MinCN im-
plies the possibility of target change of the possible
estimated outcome. Considering the relation to max-
imum pn and maximum dn, we find that high values
of MaxCN and MinCN are an effective measures of
difficulty of a particular value to be likely. Figure 5
depicts the correlation of CNS and PNS.
AND/OR
tree
framework
Minimax
tree
framework
Prove Disprove
Proof Numbers
Measures of Complexity
Maximum Maximum
Conspiracy Numbers
Measures of
Critical
Positions
Maximum
Minimum
Instability to
Lose
(Resignation)
Stability to
Win
(Surrender/
Resisting)
Difficulty to Solve
Difficulty to be
achieve likeliness
Figure 5: Correlation between CNS and PNS.
5 CONCLUDING REMARKS
In this article, we presented two main contributions:
ICAART2015-InternationalConferenceonAgentsandArtificialIntelligence
44

• The application of conspiracy numbers as the crit-
ical position identifier in the context of tic-tac-toe
game (two-players perfect information games).
• The theoretical correlation of maximum and min-
imum conspiracy numbers to maximum proof
numbers and maximum disproof numbers.
In the results presented, we successfully identi-
fied the critical position through maximum and mini-
mum conspiracy numbers in most cases of game sets.
However, not all game sets support the findings antic-
ipated from the value of the maximum and minimum
conspiracy numbers. Furthermore, further evidences
are needed in order to conclude the conspiracy num-
bers as the most suitable critical position identifier.
In addition, by determining this critical position, pos-
sible application of speculative play can be explored
and exploited to improve the overall game excite-
ment. Further explorations on larger and more com-
plex game searches (othello, chess, and endgames of
difficult positional chess) is the outlook which we will
focuses in future studies in order to give a more accu-
rate and extensive understanding on the role of CNS
as critical position identifier. Similarly, future work
on CNS as critical position identifier will potentially
reinforce claims made on its correlation to PNS.
REFERENCES
Allis, L. V., van der Meulen, M., and Van Den Herik, H. J.
(1994). Proof-number search. Artificial Intelligence,
66(1):91–124.
Buro, M. (1999). From simple features to sophisticated
evaluation functions. In Computers and Games, pages
126–145. LNCS 1558, Springer.
Carmel, D. and Markovitch, S. (1993). Learning models
of opponent’s strategy in game playing. Technion-
Israel Institute of Technology, Center for Intelligent
Systems.
Donkers, J. (2003). Nosce Hostem: Searching with Oppo-
nent Models. PhD thesis, Universiteit Maastricht.
Elkan, C. (1989). Conspiracy numbers and caching for
searching and/or trees and theorem-proving. In IJCAI,
pages 341–348.
Iida, H., Uiterwijk, J., Herik, H. J. v. d., and Herschberg,
I. (1993). Potential applications of opponent-model
search: Part 1. the domain of applicability. ICCA Jour-
nal, 16(4):201–208.
Iida, H., Uiterwijk, J., Herik, H. J. v. d., and Herschberg,
I. (1994). Potential applications of opponent-model
search. part 2: risks and strategies. ICCA Journal,
17(1):10–14.
Ishitobi, T., Cincotti, A., and Iida, H. (2013). Shape-
keeping technique and its application to checkmate
problem composition. In Ninth Artificial Intelligence
and Interactive Digital Entertainment Conference.
Jansen, P. (1992). Using knowledge about the opponent in
game-tree search. PhD thesis, Carnegie Mellon Uni-
versity.
Kishimoto, A., Winands, M. H., M¨uller, M., and Saito, J.-T.
(2012). Game-tree search using proof numbers: The
first twenty years. ICGA Journal, (3).
Lorenz, U., Rottmann, V., Feldmann, R., and Mysliwietz, P.
(1995). Controlled conspiracy number search. ICCA
Journal, 18(3):135–147.
McAllester, D. A. (1985). A new procedure for growing
min-max trees. Technical report, Artificial Intelli-
gence Laboratory, MIT, Cambridge, MA, USA.
McAllester, D. A. (1988). Conspiracy numbers for min-max
search. Artificial Intelligence, 35(3):287–310.
McAllester, D. A. and Yuret, D. (1993). Alpha-beta-
conspiracy search.
Neumann, L. J. and Morgenstern, O. (1947). Theory of
games and economic behavior, volume 60. Princeton
university press Princeton, NJ.
Ramon, J., Jacobs, N., and Blockeel, H. (2002). Opponent
modeling by analysing play. In Proceedings of Work-
shop on agents in computer games. Citeseer.
Schaeffer, J. (1989). Conspiracy numbers. Advances in
Computer Chess, 5:199–218.
Schaeffer, J. (1990). Conspiracy numbers. Artificial Intelli-
gence, 43(1):67–84.
Schaeffer, J. and van den Herikb, J. (2002). Games, com-
puters, and artificial intelligence. Chips Challenging
Champions: Games, Computers and Artificial Intelli-
gence, 3.
Shannon, C. E. (1950). Xxii. programming a computer for
playing chess. Philosophical magazine, 41(314):256–
275.
van den Herik, H. J., Donkers, H., and Spronck, P. H.
(2005). Opponent modelling and commercial games.
In Proceedings of the IEEE 2005 Symposium on Com-
putational Intelligence and Games (CIG05), pages
15–25.
van der Meulen, M. (1990). Conspiracy-number search.
ICCA Journal., 13(1):3–14.
CriticalPositionIdentificationinGamesandItsApplicationtoSpeculativePlay
45
