Veto Values in Group Decision Making within MAUT

Aggregating Complete Rankings Derived from Dominance Intensity Measures

Antonio Jim

enez-Mart

ın, Pilar Sabio and Alfonso Mateos

Departamento de Inteligencia Artiﬁcial, ETSI Inform

aticos, Universidad Polit

ecnica de Madrid,

Campus de Montegancedo S/N, Boadilla del Monte, Spain

Keywords:

Multi-attribute Utility Theory, Veto, Ordinal Information, Dominance Intensity Measures.

Abstract:

We consider a group decision-making problem within multi-attribute utility theory, in which the relative im-

portance of decision makers (DMs) is known and their preferences are represented by means of an additive

function. We allow DMs to provide veto values for the attribute under consideration and build veto and adjust

functions that are incorporated into the additive model. Veto functions check whether alternative performances

are within the respective veto intervals, making the overall utility of the alternative equal to 0, whereas adjust

functions reduce the utilty of the alternative performance to match the preferences of other DMs. Dominance

measuring methods are used to account for imprecise information in the decision-making scenario and to de-

rive a ranking of alternatives for each DM. Speciﬁcally, ordinal information about the relative importance of

criteria is provided by each DM. Finally, an extension of Kemeny’s method is used to aggregate the alternative

rankings from the DMs accounting for their relative importance.

1 INTRODUCTION

The additive model is considered a valid approach

in many practical situations for the reasons described

in (Raiffa, 1982) and (Stewart, 1996). Its functional

form is

u(A

) =

∑

j=1

i j

), (1)

where x

i j

is the performance over the attribute (or cri-

terion) X

for the alternative A

, u

is the component

utility function and w

is the weight, respectively, for

attribute X

. Note that

∑

j=1

= 1 and w

≥ 0.

The additive model is a compensatory model in

the sense that poor performance for an attribute can

be compensated by good performances for other at-

tributes.

For some multicriteria decision analysis (MCDA)

problems and certain attributes, however, DMs may

ﬁnd it convenient to provide a veto value that identi-

ﬁes attribute performances that rule out the alternative

regardless of the value taken in the other attributes.

In a group decision-making context, moreover, more

than one DM could provide different veto values for

different attributes.

For example, let us consider a couple who decide

to buy a home, so both have veto power. They iden-

tify several criteria for selecting the house, like the

price, the location, the size or the age. One of the

two might rule out any house smaller than 40m

, re-

gardless of house price, location and age, whereas the

other might rule out any smaller than 60 m

. There-

fore, in this group decision-making scenario, a pos-

sible veto range would be [0, 40], ruling out the pur-

chase of any house smaller than 40m

, and a possible

adjust range would be (40, 60], decreasing the utility

of the respective house to account for the DM veto

values.

The veto concept has been variously considered

as a real-world approach for representing the lim-

its of DM preferences in the literature.To establish

these preferences the veto threshold is represented as

a quantiﬁable measure, which becomes an important

tool in multicriteria and group decision-making.

In social theory, the concept of veto is justiﬁed by

the prudence axiom enunciated by Arrow and Ray-

naud (Arrow and Raynaud, 1986), whose main idea

is that it is not prudent to accept highly conﬂicting al-

ternatives that may result in vulnerable decisions. Re-

garding the previous axiom, Moulin deﬁnes the prin-

ciple of proportional veto in a group of DMs (Moulin,

1981), according to which any subset has the right to

veto a number of alternatives in proportion to the size

of the subgroup.

In MCDM problems the concept of veto has been

Jiménez-Martín A., Sabio P. and Mateos A..

Veto Values in Group Decision Making within MAUT - Aggregating Complete Rankings Derived from Dominance Intensity Measures.

DOI: 10.5220/0005180100990106

In Proceedings of the International Conference on Operations Research and Enterprise Systems (ICORES-2015), pages 99-106

ISBN: 978-989-758-075-8

 2015 SCITEPRESS (Science and Technology Publications, Lda.)

used for the management of non-compensatory meth-

ods. In outranking methods the use of veto usually

represents the intensity of preference of the minority

(Roy and Slowinski, 2008). Nowak used ELECTRE-

III to build a multi-attribute ranking using preference

thresholds to distinguish situations of strict and weak

preference in stochastic dominance approaches (No-

vak, 2004). Later, Munda (2009) implemented a veto-

based threshold using fuzzy set theory to represent

qualitative information.

Moreover, additive compensatory methods have

also incorporated the concept of veto. An example

is the technique for order preference by similarity to

ideal solution (TOPSIS) method (Yoon, 1980). The

basic idea behind TOPSIS is that the selected alter-

native should be as close to the ideal solution as far

from the anti-ideal solution. Both alternatives behave

like veto thresholds, not in the strict sense of rejection

of alternatives but as reference points for solving the

decision-making problem.

(Bana e Costa et al., 2002) deﬁnes a multi-criteria

approach for prohibiting alternatives based on the

measuring attractiveness by a categorical based eval-

uation technique (MACBETH). The methodological

basis of this technique is indirectly related to the con-

cept of veto power used in the non-compensatory

models.

In connection with research based on the power of

veto, (Marichal, 2004) proposes to axiomatize indi-

vidual indices to valuate when each criterion behaves

as a veto or for an aggregation by means of the Cho-

quet integral. These indices make it possible to iden-

tify and measure the impact or trend of each criterion

within the overall evaluation of the alternatives. In

(Liginlala and Ow, 2006) the same idea of the effects

of veto is used, expressing degrees of conjunction,

disjunction, veto and approval given by the indices

through fuzzy analysis measures, which represent a

risk tolerance measure of the DM.

More recently, Daher and Almeida (Daher and

Almeida, 2012) developed an additive group prefer-

ence model that incorporates a utility reduction factor.

DMs express their preferences in terms of a ranking

of alternatives and are able to make an informed veto

by providing information about the undesirable or un-

acceptable ranking of some alternatives. The ranking

veto is achieved by using a reduction factor on the

global utility of the alternatives.

In this paper we consider that veto values provided

by DMs are applicable on alternative performances

rather than on alternative rankings. We propose an ad-

ditive multi-attribute value model accounting for the

concepts of veto and adjust ranges. Different DMs

with veto power identify a veto value on each attribute

to express the limits of their preferences. They consti-

tute the basis for constructing veto and adjust ranges,

thus extending the classical additive model.

All DMs provide veto values, but the correspond-

ing veto will be effective for only the most important

DMs. These veto values are used to build a veto in-

terval, whereas veto values corresponding to the least

important DMs are used to build an adjust function

that reduces component utilities to match the prefer-

ences of other DMs.

The extension of the additive multi-attribute value

model to account for veto and adjust ranges is pro-

vided in Section 2. First, a veto and an adjust func-

tion is deﬁned on the basis of the veto values provided

by DMs. Then dominance intensity methods are in-

troduced and used to derive a ranking of alternatives

for each DM in Section 2.1. Finally, we aggregate

the ranking from the different DMs to derive a con-

sensus ranking in Section 2.2. Some conclusions are

provided in Section 3.

2 ADDITIVE MULTI-ATTRIBUTE

VALUE MODEL ACCOUNTING

FOR VETO

We consider a set of k DMs, denoted by DM

, l =

1, ..., k, whose relative importance is known and de-

noted by w

. Without loss of generality we as-

sume that the most important DM is DM

, followed

by DM

, and so on until DM

. Consequently, w

≥

≥ ... ≥ w

, and

∑

= 1.

How to measure the weights of DMs in a group

decision-making context is an interesting research

topic. (Yue, 2011) provides a brief overview of ap-

proaches proposed by different authors to determine

the weights of DMs. Morever, a new approach based

on an extended TOPSIS method is also proposed.

All DMs are allowed to provide veto values, but

the corresponding veto will be effective for only the r

most important DMs, r ≤ k. Veto values correspond-

ing to the k −r remaining DMs will be partially taken

into account, as described later.

We consider a decision-making problem with m

alternatives {A

, ..., A

} and n attributes {X

, ..., X

DM preferences are modeled by an additive multi-

attribute utility function, see Eq (1).

Ordinal information about weights is available

and each DM

provides an attribute importance rank-

ing, arranged in descending order from the most to the

least important attribute:

∈ W =

= (w

, ..., w

)|w

≥ ... ≥ w

≥ 0

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

100

and

∑

i=1

= 1.

Many methods accounting for ordinal informa-

tion on weights and alternative values/utilities within

MAVT/MAUT can be found in the literature (Sara-

bando and Dias, 2010; Punkka and Salo, 2013;

Aguayo et al., 2014; Punkka and Salo, 2014).

We denote by v

the veto threshold provided by

the l-th DM for the attribute X

, i.e. the l-th DM

wants the alternative performances to be equal to or

greater (lower) than v

if an increasing (decreasing)

component utility function is associated with attribute

. Consequently, the veto interval for the l-th DM is,

(0, v

] in attribute X

. For simplicity’s sake, we will

consider from now on that component utility func-

tions are increasing.

A veto range can then be identiﬁed in each at-

tribute [v

, v

], where v

= r

, being [r

, r

] the at-

tribute range, and v

= max

l=1,..,r

}, i.e. the high-

est veto value for attribute X

for the r most important

DMs.

We build an adjust range for each attribute X

, a

], with a

= v

= max

l=1,..,r

}, i.e. the high-

est veto value for attribute X

for the r most important

DMs, and a

= max

l=1,...,k

}, i.e. the highest veto

value for attribute X

considering all DMs.

We add the above information to the additive

multi-attribute utility function by means of the follow-

ing functions:

• v(A

) is the veto function that checks if the per-

formances for a given A

are within the respective

veto intervals:

v(A

) =

∏

j=1

with v

) =



1, if x

i j

> v

0, if x

i j

≤ v

Note that v(A

) = 0 if at least one performance

is within the veto interval for the corresponding

attribute.

• d

) is the adjust function that decreases the

utility associated with the alternative perfor-

mances within the corresponding adjust range.

One possible approach is to apply a linear adjust

function:

) =











1 if x

i j

> a

i j

−a

if a

< x

i j

≤ a

0 if x

i j

≤ a

However, we believe that the veto values for the

k − r less important DMs should be added by

means of this adjust function. Veto values pro-

vided by the k − r DMs may be within the adjust

interval. In this case, we use this information to

build a piecewise linear function.

For example, let us assume that the adjust range is

[20, 50], 50 being the highest veto value provided

by the DMs. Then, if three of the k − r less im-

portant DMs have provided the veto values 23, 28

and 35, i.e. veto values within the adjust range,

then the adjust function shown in Fig. 1 could be

plotted accounting for the above information.

Figure 1: Example of adjust function.

The adaptation of the additive multi-attribute util-

ity function to account for the veto and adjust func-

tions would be as follows:

) = [

∑

j=1

i j

)] × v(A

). (2)

This expression would then be used to derive a

ranking of the alternative under consideration for each

DM that should be aggregated taking into account

the relative importance of DMs to reach a consensus

ranking.

In the decision-making scenario under considera-

tion, however, we have assumed ordinal information

about weights, i.e. each DM has provided an attribute

importance ranking, w

. In the next section we de-

scribe how to derive an alternatives ranking on the

basis of the available ordinal information using dom-

inance measuring methods, which are based on the

notion of pairwise dominance. Then we review meth-

ods for aggregating rankings and select the best one

for our decision-making scenario, in which complete

rankings are available as well as their relative impor-

tance.

2.1 Deriving a Ranking of Alternatives

for each DM

A recent approach for dealing with imprecise infor-

mation, such as ordinal information about weights, is

VetoValuesinGroupDecisionMakingwithinMAUT-AggregatingCompleteRankingsDerivedfromDominance

IntensityMeasures

101

to compute different measures of dominance to de-

rive a ranking of alternatives (Ahn and Park, 2008;

Mateos et al., 2012; Jim

enez et al., 2013; Aguayo,

2014; Mateos et al., 2014). These approaches known

as dominance measuring methods (DMMs). DMMs

are based on the computation of a dominance ma-

trix, D, including pairwise dominance values, which

are leveraged in different ways to derive measures of

dominance to rank the alternatives under considera-

tion.

The dominance matrix for the l-th DM, D

, can be

deﬁned as follows:







− D

··· D

1(m−1)

− ··· D

2(m−1)

··· D

3(m−1)

··· D

m(m−1)

−







where

= min{u

) − u

)}

s.t.

≥ ... ≥ w

≥ 0

(3)

in our decision-making scenario accounting for veto

information, see Eq (2), and for ordinal information

about weights.

Note that given two alternatives A

and A

, alter-

native A

dominates A

if D

≥ 0, and there exists at

least one combination of weights such that the over-

all value of A

is strictly greater than that of A

. This

concept of dominance is called pairwise dominance.

The optimization problems to be solved to de-

rive pairwise dominance values are linear optimiza-

tion problems. Consequently, they can be?efﬁciently

solved using the simplex method. Note that ordinal

information could also be considered in the compo-

nent utilities, i.e., providing a ranking of the alterna-

tives and also of the difference between the values of

consecutive alternatives for each attribute, as in (Sara-

bando and Dias, 2010) or (Aguayo, 2014; Aguayo

et al., 2014). Then the resulting optimization prob-

lem would likewise be linear.

As already mentioned, the dominance matrix, D

including pairwise dominance values, is used in dif-

ferent ways to derive measures of dominance to rank

the alternatives under consideration in the DMMs.

For instance, in (Mateos et al., 2014) a DMM is pro-

posed, which derives a global dominance intensity in-

dex to rank alternatives on the basis that

≤ w

(u(A

) − u(A

)) ≤ −D

∀w

| w

≥ ... ≥ w

≥ 0,

with u(A

) = (u

) × d

), ..., u

) × d

)).

The DMM is implemented as follows:

1. If D

≥ 0, then alternative A

dominates A

, and

the dominance intensity of A

over A

(DI

) is 1,

i.e., DI

= 1.

Else (D

< 0):

- If D

≥ 0, then alternative A

dominates A

and DI

= 0.

- Else (D

< 0), DI

−D

2. Calculate a global dominance intensity (GDI) for

each alternative A

, i.e. GDI

∑

s=1, s6=k

, and

rank the alternatives according to them.

The performance of this method was compared in

(Mateos et al., 2014) with other existing approaches

(surrogate weighting methods, which select a weight

vector from a set of admissible weights to represent

the set (Stillwell et al., 1981); modiﬁed classical deci-

sion rules (Salo and Hamalainen, 2001; Puerto et al.,

2000), and the DMM proposed in (Ahn and Park,

2008)), where ordinal information represents impre-

cision concerning weights.

Monte Carlo simulation was used to demonstrate

that there is, according to the paired-samples t-test, no

signiﬁcant difference between the DMM used in this

paper and the rank-order centroid weights method

(ROC), a surrogate weighting method, and that they

outperform the other methods in terms of average hit

ratios and rank-order correlations. However, ROC can

be only applied when ordinal relations regarding at-

tribute weights are provided, whereas DMM is more

generally applicable since it can also be used when the

imprecision concerning weights or even value func-

tions is represented in other ways, for example by in-

terval values, probability distributions or even fuzzy

numbers.

Note that the described dominance measuring

method is used to derive k rankings of alternatives,

i.e a ranking for each DM.

2.2 Aggregating the Ranking of

Alternatives

Different methods for aggregating rankings can be

found in the literature by different authors. (Lin,

2010) discusses three classes of methods, namely

distribution-based, heuristic, and stochastic optimiza-

tion search.

The original Thurstone scaling and its extensions

(Thurstone, 1931; Green, 1978) represent the ﬁrst

class of methods that are most appropriate for aggre-

gating many short ranked lists. Heuristic algorithms

and stochastic search methods are applicable for ag-

gregating a small number of long lists.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

102

Heuristic algorithms are deterministic, ranging

from simple arithmetic averages of ranks (Borda’s

methods, (Borda, 1981)) to Markov chains and sta-

tionary distributions, in which only pairwise ranking

information is used (Dwork et al., 2001; DeConde

et al., 2006).

Stochastic search algorithms, on the other hand,

aim at maximizing a particular criterion. They are

usually distance measure dependent, and Kemeny

optimal aggregation (which optimizes the average

Kendall distances between a candidate aggregate list

and each of the input lists) is an example. However,

it is widely recognized that computing the Kemeny

optimal aggregate is NP-hard even when the number

of ranked lists to be aggregated is small. Stochastic

search algorithms based on the cross entropy Monte

Carlo approach, such as the order explicit algorithm

(Lin and Ding, 2009), provide an alternative for ﬁnd-

ing an optimal solution while circumventing the com-

binatorial nature of the problem. Instead of imposing

a discrete uniform distribution on all the potential so-

lutions, an iterative importance sampling technique is

utilized to slowly tighten the net to place most distri-

butional mass on the optimal solution and its neigh-

bors. Extensive simulation studies were performed to

assess the performance of the method, leading to sat-

isfactory results.

Besides, (Niu et al., 2013) divides rank aggrega-

tion methods into two categories according to the way

in which rank information is used: explicit and im-

plicit rank aggregation methods. Explicit methods di-

rectly utilize rank information to deﬁne the ranking

function or the objective function, whereas, for im-

plicit methods, other information, such as pairwise

preference or list-wise ranking is ﬁrst gathered based

on the rank information and then leveraged for rank

aggregation.

Note also that the above methods can be catego-

rized taking into account whether they assume a com-

plete, partial or top k-rank ranking of the alternatives

and whether the analysis includes the relative impor-

tance of the rankings.

In our decision-making scenario, complete rank-

ings and the relative importance of such rankings (rel-

ative importance of DMs) are available. Moreover,

the values that lead to the corresponding rankings

(global dominance intensities) are also available. The

only aggregation methods that exploit all the above

information is the Kemeny method (Kemeny, 1959)

and its extensions.

As already mentioned, Kemeny optimal aggrega-

tion optimizes the average Kendall distances between

a candidate aggregate ranking and each of the input

rankings. As computing the Kemeny optimal aggre-

gate is NP-hard even when the number of ranked lists

to be aggregated is small, we have used the order ex-

plicit algorithm (OEA)(Lin and Ding, 2009) to solve

the combinatorial problem under consideration.

OEA uses a global optimization technique,

called the cross-entropy Monte Carlo method, which

searches iteratively for an optimal list that minimizes

a criterion, the sum of weighted distances between

the candidate (aggregate) list and each of the in-

put ranked lists. The method is, however, general

and amenable to any other optimization criterion. A

modiﬁed Kendall’s tau measure and the Spearman’s

footrule, as described in (Fagin et al., 2003), are used

to measure the distance between two ranked lists.

3 AN ILLUSTRATIVE EXAMPLE

We consider ﬁve DMs whose relative importance is

= 0.35 ≥ w

= 0.25 ≥ w

= 0.2 ≥ w

0.1 = w

= 0.1. Seven alternatives {A

, ..., A

} will

be analyzed on the basis of four attributes {X

, ..., X

whose ranges are [0,100] in all cases.

The corresponding veto will be effective for only

the three most important DMs. Table 1 shows the

veto values provided by the DMs. Note that except

for DM

DMs do not provide veto values for all at-

tributes and the only veto for attribute X

is provided

by DM

Table 1: Veto values for DMs.

20 15 10 20

15 10 5 -

25 10 - -

30 25 - -

27 10 - -

Each DM expresses the relative importance of the

attributes under consideration, see Table 2. We as-

sume that the four component utility functions are lin-

ear and increasing in the attribute ranges, [0, 100], for

the ﬁve DMs.

Table 2: Relative importance of attributes for DMs.

Relative importance of attributes

≥ w

Table 3 shows the alternative performances for the

four attributes under consideration as well as the veto

and adjust ranges for each attribute.

VetoValuesinGroupDecisionMakingwithinMAUT-AggregatingCompleteRankingsDerivedfromDominance

IntensityMeasures

103

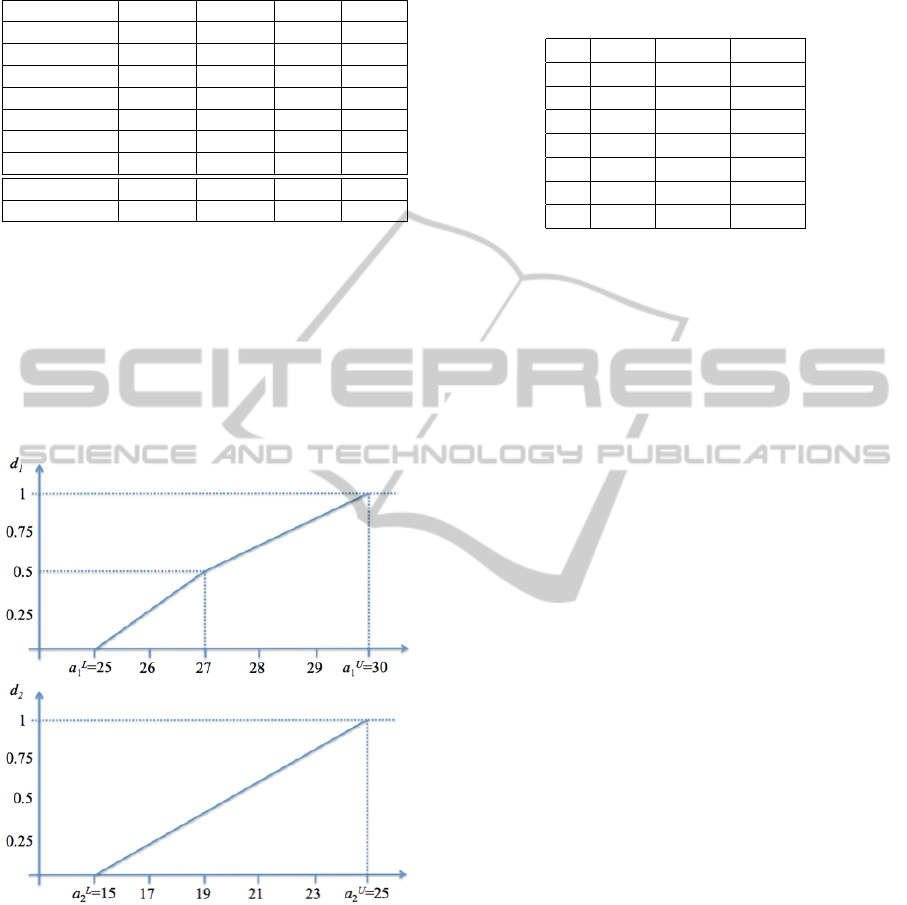
Table 3: Alternative performances and veto and adjust

ranges.

35 60 40 35

20 20 40 65

26 27 30 94

40 35 50 63

35 85 10 33

60 17 20 45

27 65 20 45

Veto range [0,25] [0, 15] [0, 10] [0, 20]

Adjust range (25, 30] (15,25] - -

The adjust functions for attributes X

and X

are

shown in Fig. 2. Note that the adjust function for at-

tribute X

is a linear function since none of the DMs

provided a veto value within the adjust range, whereas

the adjust function for attribute X

is a piecewise util-

ity function since the veto value 27 corresponding to

is within the adjust range and assigned a value

0.5.

Figure 2: Adjust functions for attributes X

and X

Table 4 shows the values output by the veto and

adjust function for the alternative performances in-

cluded in Table 3. The performances of alternatives

and A

for attributes X

and X

, respectively, are

vetoed. The utility for those alternatives will be 0, see

Eq. 2, and both will always be the two worst-ranked

alternatives and will, therefore, be worst ranked in the

consensus ranking. Consequently, we have omitted

these alternatives from further analyses.

Besides, adjust functions decrease the component

utility associated with alternatives A

and A

for at-

tribute X

and with alternatives A

and A

for attribute

Table 4: Veto and adjust values.

v(A

) d

)

1 1 1

0 0 0.5

1 0.25 1

1 1 1

0 1 1

1 1 0.2

1 0.5 1

Optimization problems can be solved using the sim-

plex method to derive the dominance matrices corre-

sponding to the ﬁve DMs. Dominance matrices are as

follows:







− .031 .05 −.248 .066

−.306 − −.334 −.532 −.224

−.099 .076 − −.198 −.017

−.171 −.07 −.149 − −.075

−.214 −.035 −.281 −.463 −













− .031 .075 −.248 .066

−.284 − −.334 −.532 −.116

−.033 .076 − −.198 .088

−.171 −.022 −.149 − −.05

−.214 −.035 −.264 −.463 −













− .031 −.099 −.024 .116

−.237 − −.266 −.216 −.116

−.033 .076 − .05 .088

−.199 −.099 −.299 − −.05

−.207 −.099 −.299 −.231 −













− −.067 −.143 −.248 .066

−.284 − −.334 −.532 −.069

.045 .075 − −.198 .111

−.104 −.072 −.149 − −.037

−.214 −.173 −.281 −.463 −













− .008 −.045 .072 −.049

−.329 − −.207 −.148 −.378

−.249 .035 − .058 −.298

−.564 −.235 −.315 − −.613

−.082 −.035 −.111 .037 −







Note that the alternatives corresponding to the rows

and columns of the above dominance matrices are A

, A

and A

, since A

and A

were removed

from the analysis.

The dominance measuring method described in

the previous section is then applied to compute global

dominance intensities (GDIs) for each DM on the ba-

sis of which to derive the corresponding ranking of

the considered alternatives.

Table 5 shows the GDIs associated with each alter-

native, whereas Table 6 shows the resulting rankings

of alternatives for the DMs under consideration.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

104

Table 5: Global dominance intensities.

5.4 5.4 5.1 4.1 5.5

2.2 2.3 2.8 3.0 2.7

4.3 4.4 5.7 5.4 4.4

4.9 5.0 3.6 5.1 2.4

3.1 2.9 2.7 2.4 5.0

Table 6: Alternative rankings for DMs.

Finally, Lin and Din’s method (OEA) is used to

aggregate the rankings in Table 6 also taking into ac-

count the relative importance of such rankings (rel-

ative importance of DM), w

= 0.35 ≥ w

0.25 ≥ w

= 0.2 ≥ w

= 0.1 = w

= 0.1, to

derive the consensus ranking shown in Table 7.

Table 7: Consensus ranking.

Alternative

Note that alternative A

is best ranked in the con-

sensus ranking, followed by A

and A

. Alternative

was best ranked by the two most important DMs

(DM

and DM

) and by DM

, whereas it was placed

second by DM

. Although alternative A

was ﬁrst

ranked by DM

and DM

, the relative importance of

both DMs in the consensus is only 0.3, and A

placed third by the other three DMs.

Note also that the ranking for DM1 matches the

consensus ranking. A sensitivity analysis was carried

out to identify the weight of DM

for which the con-

sensus ranking differed. To do this, w

DM1

is progres-

sively decreased, the remaining weights proportion-

ally updated and the consensus ranking recomputed.

The value for w

DM1

that makes the consensus rank-

ing different than the DM

’s ranking is 0.2166, and

the corresponding consensus ranking is A

, A

and A

. We found that A

is the best-ranked alter-

native no matter what the value of w

DM1

is.

4 CONCLUSIONS

In this paper we have extended the additive multi-

attribute utility model to incorporate the concept of

veto as an approximation to real situations to repre-

sent the limits of the DM preferences.

Although all DMs are allowed to provide veto val-

ues, the corresponding vetoes are effective for only

the most important DMs. They are used to deﬁne

veto ranges. Veto values corresponding to the other

less important DMs are partially taken into account,

leading to the construction of adjust ranges. A veto

and an adjust function are then incorporated into the

additive model.

A dominance measuring method is used to ac-

count for imprecise information (ordinal information

about weights) in the decision-making scenario and to

derive the ranking of alternatives, whose performance

has been analyzed in the literature using Monte Carlo

simulation techniques.

Finally, Kemeny’s method was selected to aggre-

gate the alternative rankings from the DMs since it is

the method that best ﬁts the decision-making infor-

mation, i.e. both complete rankings (and the respec-

tive global dominance intensities) and their relative

importance are available.

As computing the Kemeny optimal aggregate is

NP-hard, a stochastic search method, the order ex-

plicit algorithm proposed by Lin and Din, was used

to solve this combinatorial problem.

We propose the possibility of using trapezoidal

fuzzy numbers to aggregate group preferences regard-

ing the attribute weights as a future research line.

Then, a fuzzy dominance matrix would be computed

and a dominance-measuring method accounting for it

would be used to derive a fuzzy ranking of alterna-

tives for each DM. Finally, a fuzzy ranking aggrega-

tion process would be performed to derive a consen-

sus ranking.

Another research line is the study of parameter r,

i.e. the number of DMs whose vetoes are effective on

the basis of a threshold on their relative importance.

ACKNOWLEDGEMENTS

The paper was supported by the Spanish Ministry

of Science and Innovation project MTM2011-28983-

C03-03.

VetoValuesinGroupDecisionMakingwithinMAUT-AggregatingCompleteRankingsDerivedfromDominance

IntensityMeasures

105

REFERENCES

Aguayo, E. (2014). Dominance Intensity Methods for Rank-

ing of Alternatives in MCDM with Imprecise Informa-

tion. PhD thesis, Universidad Polit

ecnica de Madrid.

Aguayo, E., Mateos, A., and Jim

enez-Mart

ın, A. (2014). A

new dominance intensity method to deal with ordinal

information about a DM’s preferences within MAVT.

Knowledge-Based Systems, 69:159–169.

Ahn, B. and Park, K. (2008). Comparing methods for multi-

attribute decision making with ordinal weights. Com-

puters and Operations Research, 35:1660–1670.

Arrow, K. J. and Raynaud, H. (1986). Social Choice and

Multicriterion Decision Making. MIT Press, Cam-

bridge.

Bana e Costa, C., Corr

ea, E., DeCorte, J. M., and Vansnick,

J. C. (2002). Faciliting bid evalutation in public call

for tenders: a social-technical approach. OMEGA.

The International Journal of Management Science,

30:227–242.

Borda, J. (1981). Memoire sur les elections au scrutin. His-

toire de l’Academie des Sciences.

Daher, S. and Almeida, A. (2012). The use of ranking veto

concept to mitigate the compensatory effects of addi-

tive aggregation in group decisions on a water utility

automation investment. Group Decision and Negotia-

tion, 21:185–204.

DeConde, R., Hawley, S., Falcon, S., Clegg, N., Knudsen,

B., and Etzioni, R. (2006). Combining results of mi-

croarray experiments: a rank aggregation approach.

Statistical Applications in Genetics and Molecular Bi-

ology, 5:5–15.

Dwork, C., Kumar, R., Naor, M., and Sivakumar, D. (2001).

Rank aggregation methods for the web. In Proceed-

ings of the 10th International World Wide Web Con-

ference.

Fagin, R., Kumar, R., and Sivakumar, D. (2003). Compar-

ing top k lists. SIAM Journal of Discrete Mathematics,

17:134–160.

Green, P. (1978). Research for Marketing Decisions.

Prentice-Hall, New Jersey.

Jim

enez, A., Mateos, A., and Sabio, P. (2013). Domi-

nance intensity measure within fuzzy weight oriented

MAUT: An application. OMEGA. The International

Journal of Management Science, 41(2):397–405.

Kemeny, J. (1959). Mathematics without numbers.

Daedalus, 88:577–591.

Liginlala, D. and Ow, T. T. (2006). Modeling attitude to risk

in human decision processes: An application of fuzzy

measures. Fuzzy Sets and Systems, 157:3040–3054.

Lin, S. (2010). Rank aggregation methods. Wiley Interdis-

ciplinary Reviews: Computational Statistics, 2:555–

570.

Lin, S. and Ding, J. (2009). Integration of ranked lists

via cross entropy Monte Carlo with applications to

mRNA and microRNA studies. Biometrics, 65:9–18.

Marichal, J. L. (2004). Tolerant or intolerant character

of interacting criteria in aggregation by the Choquet

integral. European Journal of Operations Research,

155:771–791.

Mateos, A., Jim

enez, A., and Blanco, J. (2012). Measur-

ing method performance under incomplete informa-

tion about weights. Journal of Multicriteria Decision

Analysis, 19(3-4):129–142.

Mateos, A., Jim

enez-Mart

ın, A., Aguayo, E., and Sabio,

P. (2014). Dominance intensity measuring methods

in MCDM with ordinal relations regarding weights.

Knowledge-Based Systems, 70:26–32.

Moulin, H. (1981). The proportional veto principle. Review

of Economic Studies, 48:407–416.

Niu, S., Lan, Y., Guo, J., and Cheng, X. (2013). Stochastic

rank aggregation. In Proceedings of the Twenty-Ninth

Conference on Uncertainty in Artiﬁcial Intelligence.

Novak, M. (2004). Preference and veto threshold in multi-

criteria analysis based on stochastic dominance. Euro-

pean Journal of Operations Research, 158:339–350.

Puerto, J., M

armol, A., Monroy, L., and Fern

andez, F.

(2000). Decision criteria with partial information.

IEEE Transaction in Operational Research, 7:51–65.

Punkka, A. and Salo, A. (2013). Preference programming

with incomplete ordinal information. European Jour-

nal of Operational Research, 231(1):141–150.

Punkka, A. and Salo, A. (2014). Scale dependence and

ranking intervals in additive value models under in-

complete preference information. Decision Analysis,

11:83–104.

Raiffa, H. (1982). The Art and Science of Negotiation. Haar-

vard University Press, Cambridge.

Roy, B. and Slowinski, R. (2008). Handling effects of

reinforced preference and counter-veto in credibility

of outranking. European Journal of Operations Re-

search, 188:185–190.

Salo, A. and Hamalainen, R. P. (2001). Preference ratio

in multiattribute evaluation (PRIME)-elicitation and

decision procedures under incomplete information.

IEEE Transactions on Systems, Management and Cy-

bernetics: Part A, 31:533–545.

Sarabando, P. and Dias, L. (2010). Simple procedures of

choice in multicriteria problems without precise infor-

mation about the alternatives values. Computers and

Operations Research, 37:2239–2247.

Stewart, T. (1996). Robustness of additive value function

method in MCDM. Journal of Multicriteria Decision

Analysis, 5:301–309.

Stillwell, W., Seaver, D., and Edwards, W. (1981). Com-

parison of weight approximation techniques in multi-

attribute utility decision making. Organizatorial Be-

haviour and Human Decision Processes, 28:62–77.

Thurstone, L. (1931). Rank order as a psychophysi-

cal method. Journal of Experimental Psychology,

14:187–201.

Yoon, K. (1980). System Selection by Multiple Attribute De-

cision Making. PhD thesis, Kansas State University.

Yue, Z. (2011). A method for group decision-making based

on determining weights of decision makers using

TOPSIS. Applied Mathematical Modelling, 35:1926–

1936.

ICORES2015-InternationalConferenceonOperationsResearchandEnterpriseSystems

106