
Binary Reweighted 1
-Norm Minimization for One-Bit Compressed
Sensing
Hui Wang
1,2
, Xiaolin Huang
2
, Yipeng Liu
2
, Sabine Van Huffel
2
and Qun Wan
1
1
Department of Electronic Engineering, UESTC, Chengdu, China
2
Department Electrical Engineering, ESAT-STADIUS, KU Leuven, Leuven, Belgium
Keywords: 1-Bit Compressed Sensing (CS), Binary Reweighted
1
Norm Minimization, Thresholding Algorithm.
Abstract: The compressed sensing (CS) can acquire and reconstruct a sparse signal from relatively fewer
measurements than the classical Nyquist sampling. Practical ADCs not only sample but also quantize each
measurement to a finite number of bits; moreover, there is an inverse relationship between the achievable
sampling rate and the bit depth. The quantized CS has been studied recently and it has been demonstrated
that accurate and stable signal acquisition is still possible even when each measurement is quantized to just
a single bit. Many algorithms have been proposed for 1-bit CS however, most of them require that the prior
knowledge of the sparsity level (number of the nonzero elements) should be known. In this paper, we
explored the reweighted
1
-norm minimization method in recovering signals from 1-bit measurements. It is
a nonconvex penalty and gives different weights according to the order of the absolute value of each
element. Simulation results show that our method has much better performance than the state-of-art method
(BIHT) when the sparsity level is unknown. Even when the sparsity level is known, our method can get a
comparable performance with the BIHT method. Besides,we validate our methods in an ECG signal
recovery problem.
1 INTRODUCTION
The CS theory enables reconstruction of sparse or
compressible signals from a small number of linear
measurements relative to the dimension of the signal
space. In this setting, we have
y
Φx
where
M
N
R
Φ
(
M
N
) is the measurement
system,
1N
R
x is the signal. It was shown that
K
-
sparse signals, i.e. the number of the nonzero
elements is
K
, can be reconstructed exactly if
Φ
satisfies the restricted isometry property (RIP). The
reconstruction from
y
amounts to determining the
sparsest signal that explains the measurements
y
,
i.e. solving the following optimization problem:
0
ˆ
arg min s.t.
x
xxyΦx
(1)
where
0
x
counts the number of nonzero
components of
x
. Unfortunately, the
0
is
combinatorially complex to optimize for. Instead, CS
enforces sparsity by minimizing the
1
norm of the
reconstructed signal, i.e.
1
ˆ
arg min s.t.
x
xxyΦx
(2)
In practice, CS measurements must be quantized,
which will induce error on the measurements. The
quantized CS has been studied recently and several
new algorithms were proposed. Furthermore, for
some real world problems, severe quantization may
be inherent or preferred. For example, in ADC, the
acquisition of 1-bit measurements of an analog
signal only requires a comparator to zero, which is
an inexpensive and fast piece of hardware that is
robust to amplification of the signal and other errors,
as long as they preserve the signs of the
measurements. In this paper, we will focus on the
CS problem when a 1-bit quantizer is used.
The one-bit CS framework is expressed as:
()sign
yΦx
(3)
where the sign operator is applied component-wise
on
Φx
,
1, if 0
()
1, otherwise
i
i
x
sign x
.
206
Wang H., Huang X., Liu Y., Van Huffel S. and Wan Q..
Binary Reweighted l1-Norm Minimization for One-Bit Compressed Sensing.
DOI: 10.5220/0005208802060210
In Proceedings of the International Conference on Bio-inspired Systems and Signal Processing (BIOSIGNALS-2015), pages 206-210
ISBN: 978-989-758-069-7
Copyright
c
2015 SCITEPRESS (Science and Technology Publications, Lda.)

In this setup,
M
is not only the number of
measurements acquired but also the number of bits
acquired. Thus the ratio
M
N can be considered the
“bits per coefficient” of the original
N
-length
signal. In sharp contrast to conventional CS settings,
this means that in cases where the hardware allows,
it may actually be beneficial to acquire
M
N
measurements.
Since the problem was first introduced and
studied by Boufounos and Baraniuk in 2008, it has
been studied by many people and several algorithms
have been developed. Binary iterative hard
thresholding (BIHT) is shown to perform better than
other previous algorithms, such as fixed point
continuation (FPC), matching sign pursuit (MSP),
and restricted-step shringe (RSS). The BIHT is the
algorithm for solving
1
20
ˆ
arg min ( , ( ) )
s.t. 1,
M
ii
i
y
K
x
xΦx
xx
(4)
where
0, f 0
(, )
,otherwise
ixy
xy
xy
Although the BITH algorithm performs the best, it
requires that the sparsity level
K
should be known
as a prior. In practice,
K
is always unknown.
2 THE BINARY REWEIGHTED
1
NORM MINIMIZATION
METHOD
Recently, to enhance the sparsity of
1
-norm, E.J.
Candes etc. proposed a reweighted
1
norm, X.L.
Huang et al. proposed a new non-convex penalty,
both of them are used in conventional CS, giving
different weights according to the order of the
absolute value. Inspired by these works, we propose
a modified reweighted
1
norm minimization
method and use it in 1-bit CS, hence we call it
Binary reweighted
1
norm Minimization method
(BRW).
Using the reweighted
1
norm instead of the
0
-
norm in (4), we have
11
2
ˆ
arg min( ( ,( ) ) 2 )
s.t. 1
MN
ii ii
ii
y
wx
x
xΦx
x
(5)
where
12
,,
N
ww w are positive weights, in the
sequel, it will be convenient to denote the objective
function by
1
Wx
where
W
is the diagonal matrix
with
12
,,
N
ww w on the diagonal and zeros
elsewhere. (5) can be rewritten as
1
1
2
ˆ
arg min( ( , ( ) ) 2 )
s.t. 1
M
ii
i
y
x
xΦxWx
x
(6)
This raised the immediate question: what values for
the weights will improve signal reconstruction? One
useful way is that large weights could be used to
discourage small entries in the recovered signal,
while small weights could be used to encourage
large entries, i.e. we give different weights
according to the absolute value of each element, the
bigger the absolute value is, the smaller the
corresponding weight is.
Since (6) is nonconvex and intractable. We in
this section establish a thresholding algorithm to
solve (6). Define a soft thresholding operator
()
w
x
as :
(),
()
0,
ii i i i
i
ii
xwsignx ifx w
if x w
w
x
(7)
where
12
,,
T
N
ww ww .
We can write the local optimality condition of (6) as
( ( ( )))
T
sign
w
xxΦy Φx
(8)
Then motivated by the optimality condition (8), we
derive the following iterative soft thresholding
algorithm for (6).
Algorithm: Binary reweighted soft thresholding algorithm.
Input:
M
N
R
Φ ,
1,1
M
y
,
0Miter
,
1;
Initialization:
0l
, 1hd
, 0htol ,
0 T
xΦ
y
;
while
l Miter
and
hd htol
do
Compute
1
(())
llT l
sign
βxΦy Φx;
Update
1
11
()
l
ll
i
i
norm
w
β
;
Update
1
:()
ll
w
x
β
;
Compute
1
0
()
l
hd sign
yΦx;
1ll
;
end while
return
l
l
x
x
.
BinaryReweightedl1-NormMinimizationforOne-BitCompressedSensing
207
we set
and
are positive in order to provide
stability to ensure that a zero-valued component in
l
x does not strictly prohibit a nonzero estimate at
the next step.
3 NUMERICAL RESULTS
In the simulations, we first generate a matrix
M
N
R
Φ whose elements follow i.i.d. Gaussian
distribution. Then we generate the original
K
-
sparse signal
1N
R
x . It’s non-zero entries are
drawn from a standard Gaussian distribution and
then normalized to have norm 1. Then we compute
the binary measurements
y
according to (3).
Reconstruction of
x
is performed from
y
with two
algorithms: BIHT and the Binary reweighted
1
Minimization method (labelled as BRW). Each
reconstruction in this setup is repeated for 500 trials
and with a fixed
1000N
and
10K
unless
otherwise noted. We record the average SNR,
average reconstruction angular error (
S
d ) and
average hamming distance (
H
d ) for each
reconstruction
ˆ
x
with respect to
x
, the three
metrics are defined as:
2
2
10
2
2
ˆ
ˆ
() 10log ( )SNR xxx-x
;
1
ˆˆ
( , ) arccos ,
S
d
xx xx ;
1
1
ˆˆ
(, ) ( ( ))
M
H
ii
i
dysign
M
xx Φx
.
respectively.
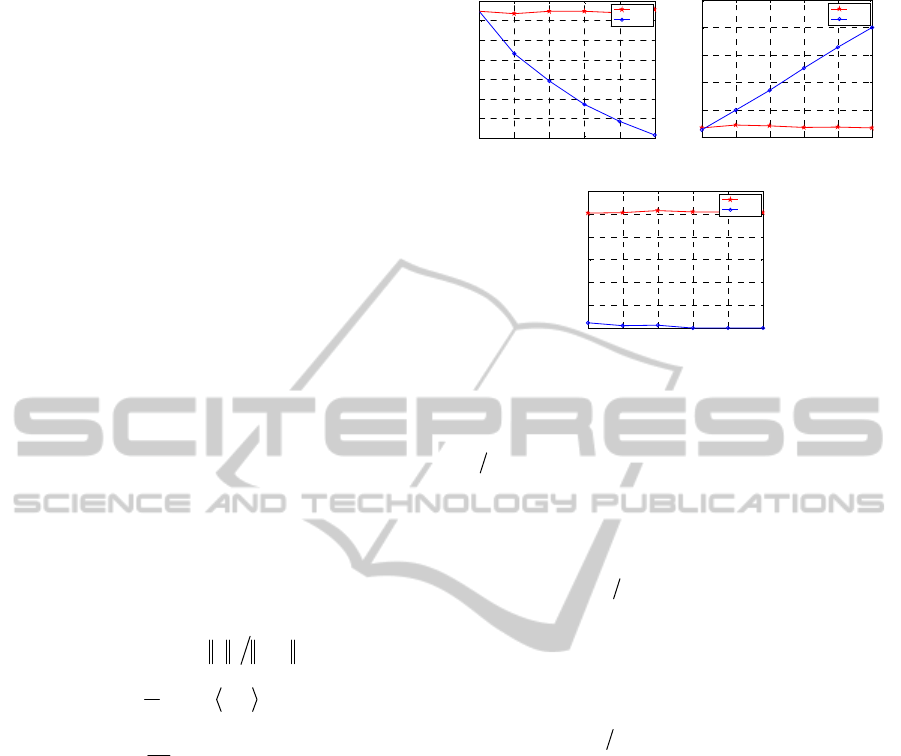
We begin by testing the two methods in the case
that
K
is unknown. We set
1000MN
,
10K
.
Since the prior knowledge of
K
should be known in
BIHT method, to demonstrate the influence of the
inaccuracy of
K
for both methods, we set
10,12,14, , 20K
instead respectively for the
BIHT method. Besides, the two parameters
and
are set to 0.35 and 0.05, respectively. The results
are shown in Fig.1. It demonstrates that the proposed
method outperforms the BIHT very much in the
SNR and average reconstruction angular error.
Fig.1(c) demonstrates that there is approximately on
average 0.5 sign differences between
y
and
ˆ
()sign Φx
.
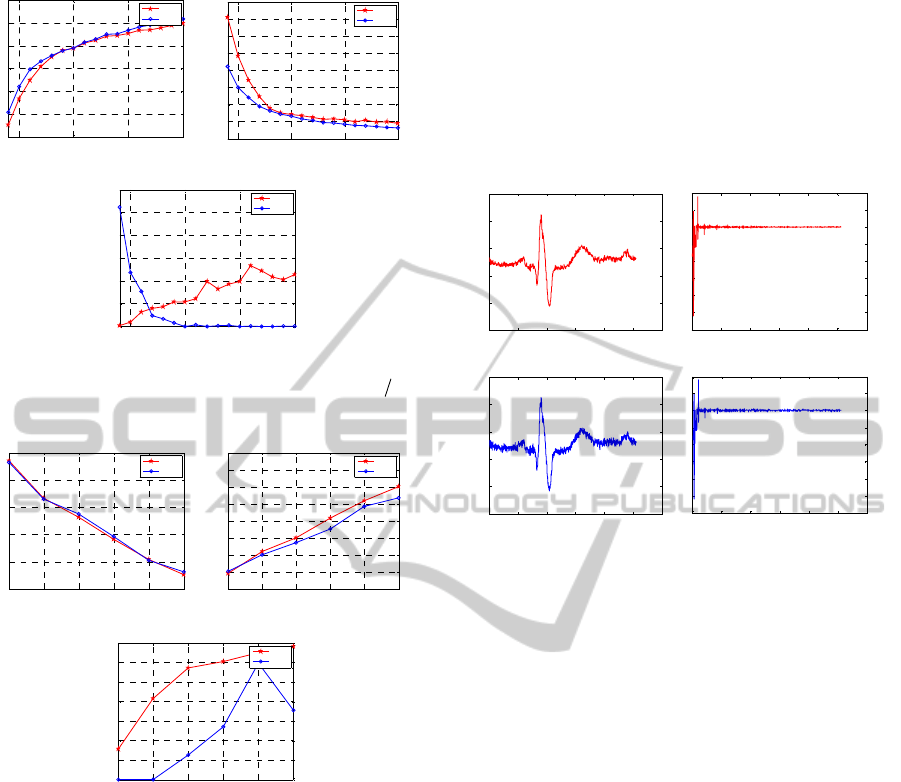
Secondly, we assume that the sparsity
K
is
known for the BIHT method. To test the
performance difference between the BIHT method
and the BRW method, we perform the trials for
(a) (b)
(c)
Figure 1: The average reconstruction error versus an
inaccurately given sparsity
K
(The actual
K
is 10 ).
M
N with in [0.4, 2].The results are depicted in
Fig.2. Then we fix
1000,MN
change
K
from
10 to 20. Still, the 3 metrics in the first experiment
are recorded. The results are shown in Fig3. From
Fig.2, we can see that in the case that
K
is known
correctly, above
0.8MN
, the average SNR and
average reconstruction angular error of the proposed
method are almost the same as that of BIHT.
Although the average hamming distance of our
method is a little poorer than the BIHT, there is
approximately only 2 sign difference between
y
and
ˆ
()
sign Φx when 2MN
. From Fig.3, we can see
that the proposed method is comparable with the
BIHT method.
In the above simulations, we have shown the
performance of the one bit reweighted
1
norm
minimization method, generally, though the method
is non-convex and global optimality cannot be
guaranteed, the algorithm for binary reweighted
1
norm minimization gives more feasible in practice.
Here, we consider real-life electrocardiography
(ECG) data as an example, and shown the ECG
signal recovery results of the one bit reweighted
1
minimization method. The used ECG data come
from the National Metrology Institute of Germany,
which is online available in PhysioNet. The record
includes 15 simultaneously measured signals
sampled from one subject simultaneously. Each
signal is digitized at 1000 samples per seconds. For
each signal channel, there are 38400 data points. We
starts from the first 1024 data and generate one
matrix
M
N
R
Φ , where
1024N
, we set that
10 12 14 16 18 20
22
24
26
28
30
32
34
36
The inaccurate sparsity K
Avg SNR (dB)
BRW
BIHT
10 12 14 16 18 20
0.005
0.01
0.015
0.02
0.025
0.03
The inaccurate sparsity K
Avg Angular Error
BRW
BIHT
10 12 14 16 18 20
0
1
2
3
4
5
6
x 10
-4
The inaccurate sparsity K
Avg Hamming Error
BRW
BIHT
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
208
(a) (b)
(c)
Figure 2: The average reconstruction error versus
M
N
when
K
is known priori.
(a) (b)
(c)
Figure 3: The average reconstruction error versus
K
.
2048M
. Then we move to the next 1024 data and
so on. The ECG data is not sparse in the time
domain as shown in Fig.4 (a), which plots
x
for time
1~1024 of signal channel no.1. We apply the
orthogonal Daubechies wavelets (db10), which is
reported to be the most popular wavelet family for
ECG compression, to design
Ψ
and get
θ
such that
xΨθ
. Then
θ
has sparsity as shown in Fig.4(b).
We generate
Φ
and compute
()signyΦΨθ
.
Then we apply the algorithm proposed in this paper
to recover
θ
. The resulted
ˆ
θ
and the corresponding
reconstructed signal
ˆ
ˆ
xΨθ
are illustrated by
Fig.4(d) and Fig.4(c), respectively. All the signals
are normalized.
From Fig.4, one can see that the binary
reweighted
1
norm minimization method can
recovery sparse pattern
. Since all the amplitude
information of the signal is lost, the reconstructed
signal lies on a unit
2
-sphere. On the other hand,
θ
is not exactly a sparse signal, so the reconstructed
results are not very good. Hence, our future work is
to solve these problems.
(a) (b)
(c)
(d)
Figure 4: The ECG signal in signal channel No.1.
4 CONCLUSIONS
In this paper, we proposed a binary reweighted
1
norm minimization method for recovering signals
from 1-bit measurements. It is a nonconvex penalty
and gives different weights according to the order of
the absolute value of each element. The simulation
results shows that the performance is much better
than the BIHT method (which has the state-of-art
performance) when the sparsity information is
unknown. Even when the sparsity is known, our
method can obtain a comparable performance with
the BIHT method.
In the future, one can consider global search
methods for the 1-bit CS. One the other hand ,since
in practice, some signals, such as the ECG data, do
not have an exactly sparse wavelet representation,
we should use more signal structure information to
enhance the 1-bit CS recovery with non-sparse
signals.
ACKNOWLEDGEMENTS
This research was supported by Research Council
0.5 1 1.5 2
15
20
25
30
35
40
45
M/N
Avg SNR (dB)
BRW
BIHT
0.5 1 1.5 2
0
0.005
0.01
0.015
0.02
0.025
0.03
0.035
0.04
M/N
Avg Angular Error
BRW
BIHT
0.5 1 1.5 2
0
0.5
1
1.5
2
2.5
3
x 10
-3
M/N
Avg Hamming Error
BRW
BIHT
10 12 14 16 18 20
26
28
30
32
34
36
Sparsity K
Avg SNR (dB)
BRW
BIHT
10 12 14 16 18 20
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0.018
0.02
Sparsity K
Avg Angular Error
BRW
BIHT
10 12 14 16 18 20
0
0.2
0.4
0.6
0.8
1
1.2
1.4
x 10
-3
Sparsity K
Avg Hamming Error
BRW
BIHT
0 200 400 600 800 1000 1200
-0.15
-0.1
-0.05
0
0.05
0.1
Time
Normalized Amplitude
0 200 400 600 800 1000 1200
-
0.6
-
0.5
-
0.4
-
0.3
-
0.2
-
0.1
0
0.1
0.2
Time
0 200 400 600 800 1000 1200
-0.15
-0.1
-0.05
0
0.05
0.1
Time
Normalized Amplitude
0 200 400 600 800 1000 1200
-0.6
-0.5
-0.4
-0.3
-0.2
-0.1
0
0.1
0.2
Time
BinaryReweightedl1-NormMinimizationforOne-BitCompressedSensing
209

KUL: GOA MaNet, PFV/10/002 (OPTEC;
FWO: G.0108.11 (Compressed Sensing) ;
G.0869.12N (Tumor imaging);
G.0A5513N (Deep brain stimulation);
IWT: TBM070713-Accelero, TBM080658-
MRI (EEGfMRI);
TBM110697-NeoGuard;
Hui Wang thanks the China Scholarship Council for
financial support.
REFERENCES
E. Candès, 2006, Compressive sampling. In Int. Congr.
Math., Madrid, Spain, vol. 3, pp. 1433–1452.
E. J. Candès, J. K. Romberg, and T. Tao, 2006. Robust un-
Certainty principles: Exact signal reconstruction from.
Highly incomplete frequency information. IEEE Trans.
Inf. Theory, vol. 52, no. 2, pp. 489–509,
E. J. Candès, J. K. Romberg, and T. Tao, 2006. Stable
signal recovery from incomplete and inaccurate
measurements. Commun. Pure Appl. Math., vol. 59,
no. 8, pp. 1207–1223.
E. J. Candès and T. Tao, 2006. Near-optimal signal
recovery from random projections: Universal encoding
strategies?. IEEE Trans. Inf. Theory, vol. 52, no. 12,
pp. 5406–5425.
D. L. Donoho, 2006. Compressed sensing. IEEE Trans.
Inf. Theory, vol.52, no. 4, pp. 1289–1306.
J. Z. Sun and V. K. Goyal, 2009. Quantization for
compressed sensing reconstruction. In Proc. Int. Conf.
Sampling Theory Appl. (SAMPTA), L. Fesquet and B.
Torrésani, Eds., Marseille, France, Special session on
sampling and quantization.
W. Dai, H. V. Pham, and O. Milenkovic, Distortionrate
functions for quantized compressive sensing. In Proc.
IEEE Inf. Theory Workshop on Netw. Inf. Theory, pp.
171–175.
A. Zymnis, S. Boyd, and E. Candes, 2010. Compressed
sensing with quantized measurements. IEEE Signal
Process. Lett., vol. 17, no. 2, pp.149–152.
J. N. Laska, P. T. Boufounos, M. A. Davenport, and R. G.
Baraniuk, 2011. Democracy in action: Quantization,
saturation, and compressive sensing. Appl. Comput.
Harmon. Anal., vol. 31, no. 3, pp. 429–443.
L. Jacques, D. K. Hammond, and M.-J. Fadili, 2011.
Dequantizing compressed sensing:When oversampling.
and non-Gaussian constraints combine”, IEEE Trans.
Inf. Theory, vol. 57, no. 1, pp. 559–571.
Y. Plan and R. Vershynin, 2012. Robust 1-bit compressed
sensing and sparse logistic regression: A convex
programming approach. [Online]. Available:
http://arxiv.org/abs/1202.1212.
P. T. Boufounos and R.G.Baraniuk, 2008. One-bit com-
pressive sensing. Presented at the Conf. Inf. Sci. Syst.
(CISS), Princeton, NJ.
J. N. Laska and R. G. Baraniuk, 2012. Regime change: bit
depth versus measurement rate in compressive
sensing”, IEEE Trans. Signal Process., vol. 60, no. 7.
L. Jacques, J. N. Laska, P. T. Boufounos, and R. G.
Baraniuk, 2011. Robust 1-bit compressive sensing via
binary stable embeddings of sparse vectors.
[Online].Available: http://arxiv.org/abs/1104. 3160.
P. T. Boufounos, 2009. Greedy sparse signal re-
construction from sign measurements. In Proc. 43rd
Asilomar Conf. Signals, Syst., Comput. pp. 1305-
1309.
J. N. Laska, Z.Wen, W.Yin, and R. G. Baraniuk , 2011.
Trust, but verify: Fast and accurate signal recovery
from 1-bit compressive measurements, IEEE Trans.
Signal Process., vol. 59, no. 11, pp. 5289–53011.
M. Bogdan, E. van den Berg, W. Su and E. J. Candès,
2013. Statistical estimation and testing via the Sorted.
L1 norm. [Online]. Available: http:// statweb.
stanford.edu/~candes/papers/SortedL1.pdf.
X. L. Huang, Yipeng Liu, Lei Shi, S. V. Huffel,
J.Suykens, 2013. Two-level ℓ1 Minimization for
Compressed Sensing. [Online]. Available: ftp://ftp.esat.
kuleuven.be/pub/SISTA/yliu/two level l1report.pdf.
G. B. Moody, R. G. Mark, and A. L. Goldberger, 2001.
PhysioNet: a webbased resource for the study of
physiologic signals. IEEE Engineering in Medicine
and Biology Magazine vol. 20, no. 3, pp.70–75.
P. S. Addison, 2005. Wavelet transforms and the ECG: a
review. Physiological Measurement, vol. 26, no. 5, pp.
R155.
BIOSIGNALS2015-InternationalConferenceonBio-inspiredSystemsandSignalProcessing
210
